Topps
Description
BenchChem offers high-quality this compound suitable for many research applications. Different packaging options are available to accommodate customers' requirements. Please inquire for more information about this compound including the price, delivery time, and more detailed information at info@benchchem.com.
Properties
IUPAC Name |
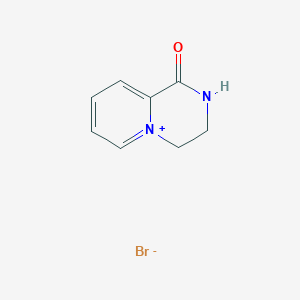
3,4-dihydro-2H-pyrido[1,2-a]pyrazin-5-ium-1-one;bromide | |
|---|---|---|
| Details | Computed by LexiChem 2.6.6 (PubChem release 2019.06.18) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
InChI |
InChI=1S/C8H8N2O.BrH/c11-8-7-3-1-2-5-10(7)6-4-9-8;/h1-3,5H,4,6H2;1H | |
| Details | Computed by InChI 1.0.5 (PubChem release 2019.06.18) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
InChI Key |
MVONIELJHBXJHP-UHFFFAOYSA-N | |
| Details | Computed by InChI 1.0.5 (PubChem release 2019.06.18) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Canonical SMILES |
C1C[N+]2=CC=CC=C2C(=O)N1.[Br-] | |
| Details | Computed by OEChem 2.1.5 (PubChem release 2019.06.18) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Molecular Formula |
C8H9BrN2O | |
| Details | Computed by PubChem 2.1 (PubChem release 2019.06.18) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Molecular Weight |
229.07 g/mol | |
| Details | Computed by PubChem 2.1 (PubChem release 2021.05.07) | |
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Foundational & Exploratory
An In-depth Technical Guide to Asymmetric Top Rotor Theory for Researchers, Scientists, and Drug Development Professionals
The study of molecular rotations provides invaluable insights into the three-dimensional structure and dynamics of molecules. This is particularly crucial in drug development, where understanding the precise conformation of a drug molecule and its interactions with biological targets is paramount. While linear and symmetric top rotors offer simplified models for molecular rotation, the vast majority of molecules, including most drug candidates, are classified as asymmetric top rotors. This guide provides a comprehensive exploration of the theory, experimental analysis, and data interpretation of asymmetric top rotors, tailored for researchers and professionals in the scientific and pharmaceutical fields.
Core Principles of Asymmetric Top Rotors
An asymmetric top rotor is a molecule with three distinct principal moments of inertia (I_a ≠ I_b ≠ I_c). By convention, these are ordered such that I_a < I_b < I_c. The corresponding rotational constants are defined as A > B > C, where:
-
A = h / (8π²cI_a)
-
B = h / (8π²cI_b)
-
C = h / (8π²cI_c)
Unlike linear and symmetric tops, the rotational energy levels of an asymmetric top cannot be expressed by a simple closed-form equation.[1] This complexity arises from the fact that the Hamiltonian operator for an asymmetric rotor is not diagonal in the basis of symmetric top wavefunctions.[2]
The Rotational Hamiltonian
The classical rotational kinetic energy of a rigid body is given by:
E = (J_a² / 2I_a) + (J_b² / 2I_b) + (J_c² / 2I_c)
where J_a, J_b, and J_c are the components of the angular momentum along the principal axes a, b, and c. The quantum mechanical Hamiltonian operator is obtained by replacing the classical angular momenta with their corresponding quantum mechanical operators:
Ĥ = AĴ_a² + BĴ_b² + CĴ_c²
Here, A, B, and C are the rotational constants in frequency units (e.g., GHz or cm⁻¹).
Energy Levels and Quantum Numbers
To determine the rotational energy levels, the Schrödinger equation, Ĥψ = Eψ, must be solved. Since a simple analytical solution is not possible, the energy levels are found by diagonalizing the Hamiltonian matrix for each value of the total angular momentum quantum number, J.[3] The wavefunctions of the asymmetric top are expressed as linear combinations of symmetric top wavefunctions.[2]
The energy levels are labeled by the total angular momentum quantum number, J, and two pseudo-quantum numbers, K_a and K_c. These subscripts indicate the K quantum number of the prolate and oblate symmetric top levels, respectively, with which the asymmetric top level correlates. The notation for a specific energy level is therefore J(K_a, K_c).
Ray's Asymmetry Parameter (κ)
The degree of asymmetry of a rotor is quantified by Ray's asymmetry parameter, κ:
κ = (2B - A - C) / (A - C)
This parameter ranges from -1 for a prolate symmetric top (B = C) to +1 for an oblate symmetric top (A = B).[4] For a truly asymmetric top, κ lies between these two extremes.
The energy levels are often expressed in terms of a reduced energy, E(κ), which is a function of κ. The total rotational energy can then be written as:
E(J, τ) = ½(A + C)J(J + 1) + ½(A - C)E_τ(κ)
where τ is an index that runs from -J to J and distinguishes the 2J+1 levels for a given J.
Rotational Spectroscopy of Asymmetric Tops
The primary experimental techniques for studying the rotational transitions of asymmetric top molecules are microwave spectroscopy and far-infrared (Fourier Transform Infrared - FTIR) spectroscopy.[1]
Selection Rules
For a molecule to have a pure rotational spectrum, it must possess a permanent electric dipole moment. The selection rules for the absorption or emission of radiation depend on the component of the dipole moment along the principal axes.[1]
The general selection rule for the total angular momentum quantum number is:
ΔJ = 0, ±1 (with J=0 ↔ J=0 forbidden)
The specific selection rules for K_a and K_c depend on the orientation of the dipole moment within the molecule, leading to different types of rotational transitions:
| Transition Type | Dipole Moment Component | ΔK_a | ΔK_c |
| a-type | μ_a | 0, ±2, ... | ±1, ±3, ... |
| b-type | μ_b | ±1, ±3, ... | ±1, ±3, ... |
| c-type | μ_c | ±1, ±3, ... | 0, ±2, ... |
Parity (even/odd) of K_a and K_c changes according to the rules above.
A molecule may exhibit transitions of more than one type if its dipole moment has components along more than one principal axis.[5]
Data Presentation: Rotational Constants of Example Asymmetric Top Molecules
The following table summarizes the ground state rotational constants for three common asymmetric top molecules. These constants are essential for predicting and analyzing their rotational spectra.
| Molecule | Formula | A (GHz) | B (GHz) | C (GHz) | κ |
| Water | H₂O | 835.83 | 435.09 | 278.37 | -0.438 |
| Formaldehyde (B43269) | H₂CO | 281.97 | 38.83 | 34.00 | -0.961 |
| Ethylene | C₂H₄ | 148.8 | 30.24 | 25.26 | -0.913 |
Note: Rotational constants can be found in various units (e.g., cm⁻¹, MHz). The values presented here are in GHz and are representative values. Experimental values can be found in the NIST Chemistry WebBook and other spectroscopic databases.[6][7][8][9][10][11][12][13][14][15][16]
Experimental Protocols
Microwave Spectroscopy of a Gaseous Sample
Objective: To obtain the high-resolution rotational spectrum of a volatile asymmetric top molecule.
Methodology:
-
Sample Preparation: The sample is introduced into the gas phase, typically by gentle heating or by utilizing its natural vapor pressure at room temperature. The pressure in the sample cell is maintained at a low level (typically a few millitorr) to minimize pressure broadening of the spectral lines.
-
Spectrometer Setup:
-
A typical microwave spectrometer consists of a microwave source (e.g., a Gunn diode or a backward-wave oscillator), a sample cell (a long metallic waveguide), and a detector (e.g., a Schottky diode).[17]
-
The microwave radiation is swept over the desired frequency range.
-
Stark modulation is often employed to enhance sensitivity. This involves applying a square-wave electric field across the sample, which splits the rotational energy levels (the Stark effect). A phase-sensitive detector (lock-in amplifier) is then used to detect only the signals that are modulated at the Stark frequency.[17]
-
-
Data Acquisition:
-
The detector output is recorded as a function of the microwave frequency.
-
The frequency is precisely calibrated using a frequency synthesizer or by referencing to known spectral standards.
-
-
Data Analysis:
-
The observed transition frequencies are measured and assigned to specific rotational transitions (J'(K'_a, K'_c) ← J''(K''_a, K''_c)).
-
The measured frequencies are then fit to the asymmetric rotor Hamiltonian to determine the rotational constants (A, B, C) and centrifugal distortion constants.
-
Fourier Transform Infrared (FTIR) Spectroscopy of a Gaseous Sample
Objective: To observe the far-infrared rotational spectrum or the rotational fine structure of vibrational bands of an asymmetric top molecule.
Methodology:
-
Sample Preparation: The gaseous sample is introduced into a gas cell with windows that are transparent to infrared radiation (e.g., KBr or CsI).[18] For studying pure rotational transitions in the far-infrared, a long path length cell (e.g., a White cell) may be necessary to achieve sufficient absorption.[19]
-
Spectrometer Setup:
-
An FTIR spectrometer, which utilizes a Michelson interferometer, is used.[20]
-
The infrared radiation from a broadband source passes through the interferometer and then through the sample cell.
-
-
Data Acquisition:
-
The transmitted radiation is detected by a suitable detector (e.g., a deuterated triglycine (B1329560) sulfate (B86663) (DTGS) or a mercury cadmium telluride (MCT) detector).
-
The resulting interferogram (a plot of intensity versus optical path difference) is recorded.
-
A background interferogram (with an empty gas cell) is also recorded.
-
-
Data Processing:
-
A Fourier transform is performed on the sample and background interferograms to obtain the single-beam spectra.
-
The sample spectrum is ratioed against the background spectrum to produce the absorbance or transmittance spectrum.
-
-
Data Analysis:
-
The frequencies of the absorption lines in the far-infrared correspond to the rotational transitions.
-
In the mid-infrared, the rotational fine structure on a vibrational band is analyzed. The spacing and pattern of the rotational lines provide information about the rotational constants in both the ground and vibrationally excited states.
-
Visualization of Key Concepts and Workflows
Signaling Pathway for Spectroscopic Analysis
Caption: Workflow for the experimental determination and analysis of an asymmetric top rotor spectrum.
Logical Relationship of Rotor Types
Caption: Correlation of asymmetric top rotors to the limiting cases of symmetric, spherical, and linear rotors.
References
- 1. ocw.mit.edu [ocw.mit.edu]
- 2. web.gps.caltech.edu [web.gps.caltech.edu]
- 3. chem.libretexts.org [chem.libretexts.org]
- 4. pubs.aip.org [pubs.aip.org]
- 5. research.cbc.osu.edu [research.cbc.osu.edu]
- 6. CCCBDB listing of experimental geometry data page 2 [cccbdb.nist.gov]
- 7. researchgate.net [researchgate.net]
- 8. Worked Example - Setting up a simple Force Field Analysis for H2O [pgopher.chm.bris.ac.uk]
- 9. High accuracy measurements on the ground state rotational spectrum of formaldehyde (H2CO) up to 2 THzElectronic supplementary information (ESI) available: Newly measured pure rotational transitions. See http://www.rsc.org/suppdata/cp/b3/b301657a/: Abstract, Citation (BibTeX) & Reference | Bohrium [bohrium.com]
- 10. High accuracy measurements on the ground state rotational spectrum of formaldehyde (H2CO) up to 2 THz - Physical Chemistry Chemical Physics (RSC Publishing) [pubs.rsc.org]
- 11. researchgate.net [researchgate.net]
- 12. pubs.aip.org [pubs.aip.org]
- 13. researchgate.net [researchgate.net]
- 14. pubs.aip.org [pubs.aip.org]
- 15. ucl.ac.uk [ucl.ac.uk]
- 16. C2H4 [cms.gutow.uwosh.edu]
- 17. fiveable.me [fiveable.me]
- 18. physics.purdue.edu [physics.purdue.edu]
- 19. Gas Measurement Using Static Fourier Transform Infrared Spectrometers - PMC [pmc.ncbi.nlm.nih.gov]
- 20. documents.thermofisher.com [documents.thermofisher.com]
An In-depth Technical Guide to Spherical Top Molecules: Properties and Implications for Drug Development
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of spherical top molecules, detailing their fundamental properties, key examples, and the experimental protocols used for their characterization. Furthermore, it explores the relevance of their unique structural features in the context of modern drug design and development.
Defining Spherical Top Molecules: A Matter of Symmetry and Inertia
In the realm of molecular physics and chemistry, molecules are classified based on the symmetry of their mass distribution, which is mathematically described by their principal moments of inertia (I_a, I_b, I_c) about three mutually perpendicular axes. A molecule is categorized as a spherical top if all three of its principal moments of inertia are equal (I_a = I_b = I_c). This high degree of rotational symmetry is a direct consequence of the molecule belonging to a cubic point group, such as tetrahedral (T_d), octahedral (O_h), or icosahedral (I_h).
The defining characteristic of spherical top molecules is their high symmetry. Due to this symmetry, they possess no permanent electric dipole moment. This has profound implications for their interaction with electromagnetic radiation, rendering them inactive in pure rotational (microwave) spectroscopy. Additionally, their polarizability is isotropic, meaning it is the same in all directions, which also makes them inactive in pure rotational Raman spectroscopy. However, centrifugal distortion during rotation can induce a small dipole moment, allowing for the observation of a very weak rotational spectrum.
Vibrational transitions in spherical top molecules are governed by stringent selection rules. Fundamental transitions are only allowed to triply degenerate vibrational states. The rovibrational spectra of these molecules are distinct, often displaying P, Q, and R branches, analogous to the perpendicular vibrations observed in linear molecules.
Prominent Examples of Spherical Top Molecules
Several well-known molecules exhibit the properties of a spherical top. The following table summarizes key quantitative data for some of the most common examples.
| Molecule | Formula | Point Group | Bond | Bond Length (Å) | Rotational Constant (B₀) (cm⁻¹) |
| Methane | CH₄ | T_d | C-H | 1.087 | 5.241 |
| Carbon Tetrachloride | CCl₄ | T_d | C-Cl | 1.767 | 0.057 |
| Sulfur Hexafluoride | SF₆ | O_h | S-F | 1.561 | 0.091 |
| Buckminsterfullerene | C₆₀ | I_h | C-C (6-6 ring) | 1.401 | ~0.0028 (Calculated) |
| C-C (6-5 ring) | 1.458 |
Note: The rotational constant for C₆₀ is a calculated value as experimental gas-phase rotational spectroscopy for this molecule is exceptionally challenging.
Experimental Protocols for Characterization
The characterization of spherical top molecules primarily relies on spectroscopic techniques that can probe their vibrational and rovibrational energy levels, namely Infrared (IR) and Raman spectroscopy.
Infrared (IR) Spectroscopy
Objective: To measure the absorption of infrared radiation corresponding to allowed vibrational transitions.
Methodology:
-
Sample Preparation: The gaseous sample of the spherical top molecule is introduced into a gas cell with windows transparent to IR radiation (e.g., KBr or NaCl). The pressure of the gas is optimized to achieve sufficient absorption without significant pressure broadening of the spectral lines.
-
Instrumentation: A Fourier Transform Infrared (FTIR) spectrometer is typically employed. The setup consists of an IR source, an interferometer, the sample cell, and a detector.
-
Data Acquisition: A background spectrum of the evacuated gas cell is first recorded. The sample is then introduced, and the sample spectrum is acquired. The absorbance spectrum is obtained by taking the ratio of the sample and background spectra.
-
Analysis: The positions and intensities of the absorption bands in the rovibrational spectrum are analyzed to determine the vibrational frequencies and, in high-resolution spectra, the rotational constants and bond lengths.
Raman Spectroscopy
Objective: To observe the inelastic scattering of monochromatic light, which provides information about the vibrational modes of the molecule.
Methodology:
-
Sample Preparation: The gaseous sample is contained in a high-pressure cell with optical windows.
-
Instrumentation: A high-intensity monochromatic light source, typically a laser, is directed onto the sample. The scattered light is collected at a 90° or 180° angle to the incident beam. A spectrometer disperses the scattered light, and a sensitive detector (e.g., a CCD camera) records the Raman spectrum.
-
Data Acquisition: The spectrum of the scattered light is recorded. The Raman spectrum consists of Stokes lines (lower frequency than the incident light) and anti-Stokes lines (higher frequency).
-
Analysis: The frequency shifts of the Raman scattered light relative to the incident laser frequency correspond to the vibrational frequencies of the molecule. High-resolution Raman spectroscopy can also provide information on rotational structure.
Relevance in Drug Development
The shape and symmetry of a molecule are fundamental determinants of its biological activity.[1] In drug design, the principle of molecular recognition dictates that a drug molecule must have a complementary shape to its biological target, such as an enzyme's active site or a receptor's binding pocket, to elicit a therapeutic effect. While the direct application of highly symmetric spherical top molecules as drugs is not common, the underlying principles of their structure are highly relevant to drug development professionals.
Shape Complementarity and Binding Affinity
The high degree of symmetry in spherical top molecules provides an idealized model for understanding the importance of shape in molecular interactions. For a drug to bind effectively to its target, a high degree of shape complementarity is required. Computational modeling techniques in drug discovery often use shape-based screening to identify potential drug candidates that can fit into a target's binding site. The spherical shape represents the most compact structure for a given volume and can be a useful starting point or fragment in the design of ligands that need to occupy globular cavities in proteins.
Symmetry and Binding Entropy
Recent studies have highlighted the role of ligand symmetry in influencing the thermodynamics of drug-receptor binding. A highly symmetric ligand can bind to a symmetric or pseudo-symmetric binding site in multiple, energetically equivalent orientations. This can lead to a significant increase in the binding entropy, which in turn can contribute to a more favorable free energy of binding and, consequently, higher binding affinity. While perfect spherical symmetry is rare in drug molecules, the principle of designing ligands with symmetry elements that match those of the target binding site is a promising strategy for enhancing potency.
Computational Modeling and Drug Design
The well-defined and rigid structures of spherical top-like molecules make them excellent systems for calibrating and validating computational models used in drug design. These models are crucial for predicting the binding affinity and mode of interaction of a drug candidate with its target. By accurately reproducing the known properties of highly symmetric molecules, researchers can have greater confidence in the predictive power of their computational tools when applied to more complex, drug-like molecules.
Conclusion
Spherical top molecules, defined by their high symmetry and equal moments of inertia, represent a unique class of chemical entities. Their distinct spectroscopic properties necessitate specialized experimental techniques for their characterization. While not typically used as drugs themselves, the principles of their shape and symmetry offer valuable insights for drug development professionals. Understanding the role of molecular shape in receptor binding and the potential for leveraging symmetry to enhance binding entropy are key considerations in the rational design of novel and more effective therapeutics. The continued study of these highly symmetric systems will undoubtedly contribute to the advancement of both fundamental molecular physics and the applied science of drug discovery.
References
The Rotational Dance of Molecules: A Technical Guide to Principal Moments of Inertia
For Researchers, Scientists, and Drug Development Professionals
In the intricate world of molecular mechanics, the way a molecule tumbles and spins holds profound implications for its physical, chemical, and biological properties. This rotational motion is elegantly described by the principal moments of inertia, a set of three fundamental values that encapsulate the distribution of mass within a molecule. This in-depth technical guide explores the core concepts of principal moments of inertia, from their theoretical underpinnings and experimental determination to their critical role in modern drug discovery and development.
Theoretical Framework: Defining Molecular Rotation
At its core, the rotation of a molecule is characterized by its moment of inertia tensor (I) , a 3x3 matrix that relates the angular velocity of the molecule to its angular momentum.[1] For a molecule composed of N atoms, the elements of this tensor are calculated based on the mass (mi) and coordinates (xi, yi, zi) of each atom relative to the molecule's center of mass.[2]
By diagonalizing the moment of inertia tensor, we obtain three eigenvalues, which are the principal moments of inertia (IA, IB, and IC), and their corresponding eigenvectors, which define the orientation of the principal axes of rotation .[1][2] These axes represent the three mutually perpendicular directions about which the molecule can rotate without wobbling.
The relationship between the principal moments of inertia allows for the classification of molecules into distinct rotational categories:
-
Spherical Tops: All three principal moments of inertia are equal (IA = IB = IC). These molecules, such as methane (B114726) (CH4) and sulfur hexafluoride (SF6), possess high symmetry.[1][3]
-
Symmetric Tops: Two of the three principal moments of inertia are equal. These are further divided into:
-
Asymmetric Tops: All three principal moments of inertia are different (IA ≠ IB ≠ IC). The majority of molecules, including water (H2O), fall into this category.[1][3]
-
Linear Molecules: One moment of inertia is zero, and the other two are equal (IA = 0, IB = IC). Examples include carbon dioxide (CO2) and hydrogen chloride (HCl).[3]
The following diagram illustrates the relationship between the moment of inertia tensor and the principal moments of inertia.
References
Classification of Polyatomic Molecules by Symmetry: An In-depth Technical Guide
For Researchers, Scientists, and Drug Development Professionals
This guide provides a comprehensive overview of the classification of polyatomic molecules based on their symmetry properties. It delves into the theoretical underpinnings of group theory in chemistry, details experimental methodologies for symmetry determination, and explores the critical role of molecular symmetry in drug design and development.
Core Concepts in Molecular Symmetry
The symmetry of a molecule is a fundamental concept that describes the indistinguishable orientations of the molecule after a symmetry operation is performed.[1] This intrinsic property is governed by the presence of symmetry elements.
Symmetry Elements and Operations
There are five fundamental symmetry elements and their corresponding symmetry operations that define the symmetry of a molecule:[2][3]
-
Identity (E): This operation consists of doing nothing to the molecule. Every molecule possesses the identity element.[1]
-
Proper Rotation Axis (C_n_): An axis around which a rotation by 360°/n leaves the molecule in an indistinguishable orientation. The axis with the highest value of 'n' is termed the principal axis.[1]
-
Plane of Symmetry (σ): A mirror plane that divides the molecule into two identical halves. There are three types of symmetry planes:
-
Inversion Center (i): A point within the molecule through which if every atom is projected, an identical atom is found at an equal distance on the opposite side.[1][2]
-
Improper Rotation Axis (S_n_): An axis around which a rotation by 360°/n followed by a reflection in a plane perpendicular to the axis leaves the molecule unchanged.[1]
Point Groups
The complete set of symmetry operations that can be performed on a molecule constitutes a mathematical group known as a point group .[4][5] Each molecule can be assigned to a specific point group, which succinctly summarizes its symmetry. The assignment of a point group is a systematic process, often facilitated by a flowchart, that identifies all the symmetry elements present in the molecule.[6][7][8]
Assigning Point Groups: A Logical Approach
The following diagram illustrates a decision-making workflow for assigning a molecule to its correct point group.
Experimental Determination of Molecular Symmetry
Several experimental techniques are employed to elucidate the three-dimensional structure of molecules, from which their symmetry can be determined.
X-ray Crystallography
This is a powerful technique for determining the precise arrangement of atoms in a crystalline solid.[7][9]
Methodology:
-
Crystal Growth: High-quality single crystals of the molecule of interest are grown from a supersaturated solution. The slow growth of crystals is crucial for obtaining a well-ordered lattice.[4]
-
Crystal Mounting: A suitable crystal (typically 0.1-0.3 mm in size) is selected under a microscope and mounted on a goniometer head.[10][11]
-
Data Collection: The crystal is placed in an X-ray diffractometer and irradiated with a monochromatic X-ray beam. The crystal is rotated, and the diffraction pattern (the intensities and positions of the diffracted X-rays) is recorded by a detector.[12]
-
Structure Solution: The diffraction data is processed to determine the unit cell dimensions and the space group of the crystal. The "phase problem" is solved using computational methods to generate an initial electron density map.[10]
-
Structure Refinement: The atomic model is built into the electron density map and refined to best fit the experimental data. This process yields the final three-dimensional structure of the molecule, including bond lengths and angles, from which the molecular symmetry can be determined.[10]
Vibrational Spectroscopy (Infrared and Raman)
Infrared (IR) and Raman spectroscopy probe the vibrational modes of a molecule. The number of IR and Raman active modes is directly related to the molecule's symmetry.[13][14]
Methodology:
-
Point Group Determination: The point group of the molecule is first determined based on its known or predicted geometry.
-
Reducible Representation: A reducible representation (Γ_total_) for all 3N degrees of freedom of the molecule is generated by considering the effect of each symmetry operation of the point group on the Cartesian coordinates of each atom.[5]
-
Irreducible Representations: The reducible representation is then reduced to a sum of irreducible representations using the character table for that point group.
-
Translational and Rotational Modes: The irreducible representations corresponding to translational and rotational motion are subtracted from the total to obtain the irreducible representations of the vibrational modes (Γ_vib_).
-
IR and Raman Activity: The character table is used to determine which of the vibrational modes are IR active (transform as the x, y, or z coordinates) and which are Raman active (transform as the binary products of coordinates like x², y², z², xy, xz, or yz).[5] By comparing the predicted number of IR and Raman active bands with the experimental spectra, the point group of the molecule can be confirmed.
Nuclear Magnetic Resonance (NMR) Spectroscopy
NMR spectroscopy provides information about the chemical environment of nuclei within a molecule. The chemical equivalence of nuclei is determined by the symmetry of the molecule.[4]
Methodology:
-
Sample Preparation: A sample of the compound is dissolved in a suitable deuterated solvent. It is crucial to use the correct amount of material and ensure the sample is free of solid particles.[15][16][17]
-
Data Acquisition: The sample is placed in the NMR spectrometer, and a spectrum is acquired. For symmetry analysis, ¹H and ¹³C NMR are most common.
-
Spectral Analysis: The number of signals in the NMR spectrum corresponds to the number of chemically non-equivalent sets of nuclei.
-
Homotopic nuclei: Nuclei that can be interchanged by a C_n_ axis are chemically equivalent and give a single signal.
-
Enantiotopic nuclei: Nuclei that can be interchanged by a σ plane are chemically equivalent in an achiral solvent and give a single signal.
-
Diastereotopic nuclei: Nuclei that cannot be interchanged by any symmetry operation are chemically non-equivalent and give distinct signals.
-
-
Symmetry Determination: By analyzing the number and multiplicity of signals in the NMR spectrum, one can deduce the symmetry elements present in the molecule and thus infer its point group.
Quantitative Data: Character Tables
Character tables are essential tools in the application of group theory to chemistry. They provide a concise summary of the symmetry properties of a point group and its irreducible representations.
Table 1: Character Table for the C_2v_ Point Group (e.g., H₂O)
| C_2v_ | E | C₂ | σ_v_(xz) | σ_v'(yz) | Linear, Rotations | Quadratic |
| A₁ | 1 | 1 | 1 | 1 | z | x², y², z² |
| A₂ | 1 | 1 | -1 | -1 | R_z | xy |
| B₁ | 1 | -1 | 1 | -1 | x, R_y_ | xz |
| B₂ | 1 | -1 | -1 | 1 | y, R_x_ | yz |
Table 2: Character Table for the C_3v_ Point Group (e.g., NH₃)
| C_3v_ | E | 2C₃ | 3σ_v_ | Linear, Rotations | Quadratic |
| A₁ | 1 | 1 | 1 | z | x² + y², z² |
| A₂ | 1 | 1 | -1 | R_z_ | |
| E | 2 | -1 | 0 | (x, y), (R_x_, R_y_) | (x² - y², xy), (xz, yz) |
Table 3: Character Table for the D_3h_ Point Group (e.g., BF₃)
| D_3h_ | E | 2C₃ | 3C₂ | σ_h_ | 2S₃ | 3σ_v_ | Linear, Rotations | Quadratic |
| A₁' | 1 | 1 | 1 | 1 | 1 | 1 | x² + y², z² | |
| A₂' | 1 | 1 | -1 | 1 | 1 | -1 | R_z_ | |
| E' | 2 | -1 | 0 | 2 | -1 | 0 | (x, y) | (x² - y², xy) |
| A₁" | 1 | 1 | 1 | -1 | -1 | -1 | ||
| A₂" | 1 | 1 | -1 | -1 | -1 | 1 | z | |
| E" | 2 | -1 | 0 | -2 | 1 | 0 | (R_x_, R_y_) | (xz, yz) |
Molecular Symmetry in Drug Development
Molecular symmetry, particularly the concept of chirality (point groups C_n_ and D_n_), plays a pivotal role in drug design and action.[10][18]
Chirality and Pharmacological Activity
Many drugs are chiral, existing as a pair of non-superimposable mirror images called enantiomers.[18] These enantiomers can have vastly different pharmacological, pharmacokinetic, and toxicological properties because biological systems, such as receptors and enzymes, are themselves chiral.[18][19]
-
Eutomer: The enantiomer with the desired therapeutic activity.
-
Distomer: The other enantiomer, which may be less active, inactive, or even responsible for undesirable side effects.[8]
A classic example is the drug thalidomide , where one enantiomer was effective against morning sickness, while the other was teratogenic.[9] Another example is ibuprofen , where the (S)-(+)-enantiomer is the active anti-inflammatory agent, while the (R)-(-)-enantiomer is much less active.[1][6]
Table 4: Examples of Chiral Drugs and their Enantiomer-Specific Activity
| Drug | Eutomer (Active Enantiomer) | Therapeutic Use | Activity of Distomer |
| Ibuprofen | (S)-(+)-Ibuprofen | Anti-inflammatory | Largely inactive; undergoes in-vivo conversion to the S-form.[6] |
| Albuterol | (R)-(-)-Albuterol | Bronchodilator (Asthma) | May contribute to side effects. |
| Ethambutol | (S,S)-Ethambutol | Antitubercular | Can cause optic neuritis (toxic).[9] |
| L-DOPA | L-DOPA | Anti-Parkinson's agent | Inactive and can cause side effects.[8] |
| Omeprazole | (S)-Omeprazole (Esomeprazole) | Proton pump inhibitor | Metabolized more rapidly, leading to lower bioavailability.[1] |
Structure-Based Drug Design Workflow
The principles of molecular symmetry are integral to modern structure-based drug design (SBDD).
Signaling Pathway Example: G Protein-Coupled Receptors (GPCRs)
GPCRs are a large family of transmembrane receptors that are major drug targets.[20][21] The binding of a ligand to a GPCR initiates a conformational change that triggers an intracellular signaling cascade.[19] The stereochemistry of the ligand is often critical for selective and effective binding.
In this pathway, the chiral binding pocket of the GPCR selectively recognizes one enantiomer (the eutomer) of a chiral ligand, leading to receptor activation and a downstream cellular response. The other enantiomer (the distomer) may not bind or may bind in a way that does not elicit the same response.
Conclusion
The classification of polyatomic molecules by symmetry is a cornerstone of modern chemistry. Grounded in the mathematical framework of group theory, it provides a powerful lens through which to understand and predict molecular properties. For researchers in the pharmaceutical sciences, a deep understanding of molecular symmetry is not merely academic; it is a critical component of rational drug design, enabling the development of safer and more effective therapeutic agents. The experimental techniques outlined in this guide provide the means to determine molecular symmetry, while the application to drug development highlights its profound practical implications.
References
- 1. A Look at the Importance of Chirality in Drug Activity: Some Significative Examples [mdpi.com]
- 2. dosequis.colorado.edu [dosequis.colorado.edu]
- 3. Preparation of Single Crystals for X-ray Diffraction | Department of Chemistry | UZH [chem.uzh.ch]
- 4. chem.libretexts.org [chem.libretexts.org]
- 5. Chirality in Pharmaceuticals: The Impact of Molecular Handedness on Medicine – Chiralpedia [chiralpedia.com]
- 6. X-ray Diffraction Protocols and Methods | Springer Nature Experiments [experiments.springernature.com]
- 7. pubs.acs.org [pubs.acs.org]
- 8. Chiral drugs - Wikipedia [en.wikipedia.org]
- 9. fiveable.me [fiveable.me]
- 10. Chemistry Teaching Labs - Single Crystal X-ray Diffraction [chemtl.york.ac.uk]
- 11. Single-crystal X-ray Diffraction [serc.carleton.edu]
- 12. pubs.aip.org [pubs.aip.org]
- 13. researchgate.net [researchgate.net]
- 14. NMR Sample Preparation [nmr.chem.umn.edu]
- 15. \Basics of NMR\ Sample preparation and analysis of NMR analysis data\ - Mesbah Energy [irisotope.com]
- 16. NMR blog - Guide: Preparing a Sample for NMR analysis – Part I — Nanalysis [nanalysis.com]
- 17. Chiral Drugs: An Overview - PMC [pmc.ncbi.nlm.nih.gov]
- 18. Signaling through G protein coupled receptors - PMC [pmc.ncbi.nlm.nih.gov]
- 19. G protein-coupled receptor - Wikipedia [en.wikipedia.org]
- 20. Biochemistry, G Protein Coupled Receptors - StatPearls - NCBI Bookshelf [ncbi.nlm.nih.gov]
- 21. creative-diagnostics.com [creative-diagnostics.com]
rotational energy levels of a prolate symmetric top
An In-depth Technical Guide to the Rotational Energy Levels of a Prolate Symmetric Top
This guide provides a comprehensive overview of the rotational energy levels of prolate symmetric top molecules, intended for researchers, scientists, and professionals in drug development and related fields. It covers the theoretical underpinnings, quantum mechanical descriptions, and spectroscopic selection rules that govern these energy levels.
Introduction to Symmetric Top Molecules
In rotational spectroscopy, molecules are classified based on the relative values of their principal moments of inertia (Ia, Ib, Ic) about the three principal axes of rotation (a, b, c). A symmetric top is a molecule in which two of these moments of inertia are equal.[1]
A prolate symmetric top is characterized by having one unique, small moment of inertia (Ia) and two larger, equal moments of inertia (Ib = Ic).[2][3] This molecular shape is often compared to a cigar or an American football, where the unique axis 'a' is the symmetry axis.[2][4] Examples of prolate symmetric top molecules include methyl iodide (CH3I) and ammonia (B1221849) (NH3).[2][5]
The rotational motion of these molecules is described by rotational constants (A, B, C), which are inversely proportional to the moments of inertia. For a prolate top, the relationship is Ia < Ib = Ic, which leads to the rotational constant relationship A > B = C.[6]
Rotational Energy Levels
The rotational energy of a prolate symmetric top molecule is quantized and described by two quantum numbers: J and K.
-
J : The total angular momentum quantum number, which can take any integer value J = 0, 1, 2, ...
-
K : The quantum number for the projection of the angular momentum onto the principal symmetry axis (the 'a' axis). For a given J, K can take integer values from -J to +J (i.e., K = 0, ±1, ±2, ..., ±J).[1][2]
The energy levels, often expressed in units of wavenumber (cm-1) as rotational term values F(J, K), are given by the equation:
F(J, K) = B J(J+1) + (A - B) K2
Here, A and B are the rotational constants in wavenumber units.
Several key features arise from this equation:
-
The energy depends on J and the absolute value of K.[7]
-
Since the energy depends on K2, the energy levels are independent of the sign of K. This means that for any K > 0, the energy levels are doubly degenerate.[2][7]
-
For a given value of K, the energy levels form a "K-ladder," where the spacing between successive J levels is determined primarily by the rotational constant B.[7]
-
Since A > B for a prolate top, for a fixed value of J, the energy increases as the value of |K| increases.[5]
Spectroscopic Transitions and Selection Rules
The observation of rotational spectra is governed by selection rules, which dictate the allowed transitions between energy levels. For a prolate symmetric top molecule to have a pure rotational (microwave) spectrum, it must possess a permanent dipole moment.[5]
The selection rules for electric-dipole-allowed transitions are:
The rule ΔK = 0 signifies that radiative transitions cannot change the angular momentum component along the symmetry axis.[7] This means that spectroscopic transitions only occur between different J levels within the same K-ladder.[5]
Quantitative Data Summary
The key parameters and equations governing the are summarized in the table below.
| Parameter/Equation | Description | Allowed Values / Formula |
| Moments of Inertia | Defines a prolate symmetric top. | Ia < Ib = Ic |
| Rotational Constants | Defines a prolate symmetric top. | A > B = C |
| J Quantum Number | Total angular momentum. | J = 0, 1, 2, ... |
| K Quantum Number | Projection of J on the symmetry axis. | K = 0, ±1, ±2, ..., ±J |
| Rotational Term Value | Quantized rotational energy levels (in cm-1). | F(J, K) = B J(J+1) + (A - B) K2 |
| Selection Rules | Allowed transitions for microwave spectroscopy. | ΔJ = ±1, ΔK = 0 |
| Transition Frequency | Wavenumber of an absorption line (J → J+1). | ν = F(J+1, K) - F(J, K) = 2B(J+1) |
The frequency of an allowed absorption transition (J → J+1) can be calculated as follows: ν = F(J+1, K) - F(J, K) ν = [B(J+1)(J+2) + (A-B)K2] - [B J(J+1) + (A-B)K2] ν = B[(J2+3J+2) - (J2+J)] ν = 2B(J+1) [5][9]
This result is notable because it is independent of both the rotational constant A and the quantum number K. Consequently, the rotational spectrum for a given K-ladder consists of a series of lines separated by a constant value of 2B, which is identical to the spectrum of a linear rotor.[5]
Visualization of Energy Levels and Transitions
The following diagram illustrates the rotational energy level structure for a prolate symmetric top. It shows distinct "ladders" of energy levels for different K values. The allowed transitions (ΔJ = +1, ΔK = 0) are shown as vertical arrows within each K-ladder.
Caption: Rotational energy levels of a prolate symmetric top.
Experimental Protocols
The primary experimental technique for studying pure rotational energy levels is microwave spectroscopy .
Methodology for Microwave Spectroscopy:
-
Sample Preparation: The molecule of interest is introduced into a sample cell in the gas phase at low pressure to minimize intermolecular interactions and collisional broadening.
-
Radiation Source: A monochromatic microwave source (e.g., a klystron or Gunn diode) is used to generate radiation. The frequency of this source is swept across the desired range.
-
Interaction: The microwave radiation is passed through the sample cell. If the frequency of the radiation matches the energy difference between two allowed rotational levels (as dictated by the selection rules), the molecules will absorb the radiation.
-
Detection: A detector placed after the sample cell measures the intensity of the transmitted radiation. A decrease in intensity at specific frequencies corresponds to absorption by the sample.
-
Spectrum Generation: The absorption intensity is plotted as a function of frequency, yielding the rotational spectrum.
-
Data Analysis: The frequencies of the absorption lines are measured precisely. Since the lines in the spectrum are separated by 2B, the rotational constant B can be determined directly from the spacing.[9] By analyzing the spectra of different isotopically substituted versions of the molecule, it is possible to determine the moments of inertia and, subsequently, precise molecular bond lengths and angles.[8]
References
- 1. apps.dtic.mil [apps.dtic.mil]
- 2. youtube.com [youtube.com]
- 3. w3.iams.sinica.edu.tw [w3.iams.sinica.edu.tw]
- 4. chem.libretexts.org [chem.libretexts.org]
- 5. web.gps.caltech.edu [web.gps.caltech.edu]
- 6. m.youtube.com [m.youtube.com]
- 7. ocw.mit.edu [ocw.mit.edu]
- 8. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 9. Selection rules for rotational spectra [pci.tu-bs.de]
An In-depth Technical Guide to Oblate and Prolate Symmetric Top Molecules for Researchers, Scientists, and Drug Development Professionals
In the realms of molecular physics, spectroscopy, and computational chemistry, a precise understanding of molecular geometry is paramount. The three-dimensional arrangement of atoms dictates a molecule's physical and chemical properties, including its reactivity and interactions with biological targets. Among the various classifications of molecular shapes based on their rotational properties, symmetric top molecules represent a crucial category. This technical guide provides a comprehensive exploration of the two primary types of symmetric tops: oblate and prolate molecules. It is designed to furnish researchers, scientists, and drug development professionals with the foundational knowledge, quantitative data, and experimental insights necessary for their work.
Delineating Oblate and Prolate Symmetric Tops: The Role of Moments of Inertia
The classification of a molecule's rotational behavior hinges on its principal moments of inertia, denoted as Ia, Ib, and Ic, about three mutually perpendicular axes passing through the molecule's center of mass. By convention, these moments of inertia are ordered such that Ic ≥ Ib ≥ Ia. Symmetric top molecules are characterized by having two of their three principal moments of inertia being equal.[1][2] This equality results in a unique principal axis of symmetry.
Prolate Symmetric Tops: A molecule is classified as a prolate symmetric top if its moment of inertia about the unique principal axis (conventionally the 'a' axis) is the smallest.[3] This can be expressed as:
Ia < Ib = Ic
Physically, prolate molecules are elongated, resembling the shape of a cigar or a football.[3] This elongation means that the molecule is more massive at its ends along the principal axis, making it easier to rotate about this axis. Examples of prolate molecules include methyl iodide (CH3I), chloroform (B151607) (CHCl3), and propyne (B1212725) (CH3C≡CH).[4]
Oblate Symmetric Tops: Conversely, a molecule is categorized as an oblate symmetric top if its moment of inertia about the unique principal axis (conventionally the 'c' axis) is the largest.[3] This relationship is defined as:
Ia = Ib < Ic
Oblate molecules are flattened at the poles and bulged at the equator, analogous to a frisbee or a discus.[3] This mass distribution makes them more difficult to rotate about their principal axis of symmetry. Common examples of oblate molecules include benzene (B151609) (C6H6), ammonia (B1221849) (NH3), and boron trichloride (B1173362) (BCl3).[4][5]
The following diagram illustrates the logical workflow for classifying a molecule based on its moments of inertia.
Caption: Workflow for classifying molecular shape.
Quantitative Data Presentation
The distinction between oblate and prolate symmetric tops is quantitatively defined by their rotational constants (A, B, and C), which are inversely proportional to the moments of inertia. The relationships are given by:
A = h / (8π2cIa) B = h / (8π2cIb) C = h / (8π2cIc)
where h is Planck's constant and c is the speed of light.
For a prolate symmetric top: A > B = C For an oblate symmetric top: A = B > C
The following tables summarize the rotational constants and moments of inertia for selected oblate and prolate symmetric top molecules.
Table 1: Quantitative Data for Oblate Symmetric Top Molecules
| Molecule | Formula | A = B (GHz) | C (GHz) | Ia = Ib (amu Å2) | Ic (amu Å2) |
| Benzene | C6H6 | 5.689 | 2.845 | 88.91 | 177.8 |
| Ammonia | NH3 | 298.1 | 186.7 | 1.696 | 2.708 |
| Boron Trichloride | BCl3 | 3.15 | 1.575 | 160.5 | 321.0 |
| s-Triazine | C3H3N3 | 6.13 | 3.065 | 82.5 | 165.0 |
Table 2: Quantitative Data for Prolate Symmetric Top Molecules
| Molecule | Formula | A (GHz) | B = C (GHz) | Ia (amu Å2) | Ib = Ic (amu Å2) |
| Methyl Iodide | CH3I | 152.9 | 7.50 | 3.30 | 67.4 |
| Chloroform | CHCl3 | 5.79 | 2.89 | 87.3 | 174.9 |
| Propyne | CH3C≡CH | 154.8 | 8.55 | 3.26 | 59.1 |
| Acetonitrile | CH3CN | 155.8 | 9.20 | 3.24 | 54.9 |
Experimental Protocols for Determining Molecular Shape
The determination of a molecule's rotational constants and, consequently, its classification as oblate or prolate, is primarily achieved through high-resolution rotational spectroscopy. The two main techniques employed are microwave spectroscopy and rotational Raman spectroscopy.
Microwave Spectroscopy
Microwave spectroscopy is a highly sensitive technique for observing the rotational transitions of polar molecules in the gas phase.[6]
Methodology:
-
Sample Preparation: The molecule of interest is introduced into the gas phase at low pressure (typically a few millitorr) within a waveguide sample cell. This ensures that the molecules are sufficiently isolated to rotate freely without significant intermolecular interactions.
-
Instrumentation:
-
Microwave Source: A tunable monochromatic microwave source, such as a klystron or a Gunn diode, generates radiation in the gigahertz frequency range.[7]
-
Waveguide: The microwave radiation is directed through a waveguide containing the gaseous sample.[7]
-
Detector: A detector, typically a crystal diode, measures the intensity of the microwave radiation that passes through the sample.
-
Modulation and Detection: Stark modulation is often employed to enhance sensitivity. An oscillating electric field is applied across the sample, which modulates the rotational energy levels and, consequently, the absorption signal. A phase-sensitive detector (lock-in amplifier) is then used to selectively amplify the modulated signal, improving the signal-to-noise ratio.[7]
-
-
Data Acquisition: The frequency of the microwave source is swept over a desired range, and the detector output is recorded as a function of frequency. Absorption of microwaves occurs at frequencies corresponding to the energy difference between rotational levels.
-
Data Analysis:
-
The resulting spectrum consists of a series of absorption lines. For a symmetric top molecule, the frequencies of the rotational transitions are given by: ν = 2B(J+1) where J is the rotational quantum number of the lower state.
-
The spacing between adjacent lines in the spectrum is equal to 2B. By measuring these spacings, the rotational constant B can be determined with high precision.
-
To determine the other rotational constant (A for prolate, C for oblate), isotopic substitution is often employed. By analyzing the rotational spectra of different isotopologues of the molecule, the atomic coordinates can be determined, and from these, all three moments of inertia can be calculated.[8]
-
The following diagram illustrates the experimental workflow for microwave spectroscopy.
Caption: Workflow for microwave spectroscopy.
Rotational Raman Spectroscopy
Rotational Raman spectroscopy is a complementary technique that can be used to study the rotational transitions of non-polar molecules, which are inaccessible to microwave spectroscopy.[9]
Methodology:
-
Sample Preparation: The sample, typically in the gaseous phase, is held in a sample cell.
-
Instrumentation:
-
Light Source: An intense, monochromatic light source, usually a laser, is used to irradiate the sample.
-
Sample Illumination: The laser beam is focused into the sample cell.
-
Scattered Light Collection: The light scattered by the sample, typically at a 90-degree angle to the incident beam, is collected by a lens.
-
Spectrometer: The collected scattered light is passed through a high-resolution spectrometer to disperse the light according to its frequency.
-
Detector: A sensitive detector, such as a charge-coupled device (CCD), records the spectrum of the scattered light.
-
-
Data Acquisition: The spectrum of the scattered light is recorded. It consists of a strong central line at the laser frequency (Rayleigh scattering) and a series of weaker lines on either side (Raman scattering).
-
Data Analysis:
-
The Raman lines correspond to transitions between rotational energy levels. The selection rule for rotational Raman transitions in symmetric top molecules is ΔJ = 0, ±2.
-
The frequency shifts (Δν) of the Raman lines from the exciting laser line are given by: Δν = 4B(J + 3/2)
-
The spacing between adjacent Stokes (lower frequency) or anti-Stokes (higher frequency) lines is 4B. By measuring these spacings, the rotational constant B can be determined.
-
Rotational Energy Levels and Spectra
The rotational energy levels of a rigid symmetric top molecule are given by:
E(J, K) = B J(J+1) + (A-B)K2 for a prolate top E(J, K) = B J(J+1) + (C-B)K2 for an oblate top
where J is the total angular momentum quantum number and K is the projection of the angular momentum onto the principal symmetry axis.
The selection rules for rotational transitions observed in microwave spectroscopy are ΔJ = ±1 and ΔK = 0.[9] This leads to a simple spectrum with equally spaced lines, as described in the experimental protocol.
The following diagrams illustrate the rotational energy level structures for prolate and oblate symmetric top molecules.
Caption: Prolate top energy levels.
Caption: Oblate top energy levels.
Conclusion
The classification of molecules as oblate or prolate symmetric tops provides a fundamental framework for understanding their rotational behavior and, by extension, their physical and chemical properties. High-resolution rotational spectroscopy, particularly microwave and Raman techniques, offers the experimental means to precisely determine the moments of inertia and rotational constants that define these classifications. For researchers in fields ranging from fundamental chemical physics to drug development, a thorough grasp of these concepts and experimental methodologies is indispensable for elucidating molecular structure and function. The quantitative data and procedural outlines provided in this guide serve as a valuable resource for both theoretical and experimental investigations into the fascinating world of molecular rotation.
References
- 1. Measuring and analyzing the microwave spectra to determine the molecular structure | Sophia University [sophia.ac.jp]
- 2. youtube.com [youtube.com]
- 3. chem.libretexts.org [chem.libretexts.org]
- 4. pubs.acs.org [pubs.acs.org]
- 5. kvmwai.edu.in [kvmwai.edu.in]
- 6. fiveable.me [fiveable.me]
- 7. fiveable.me [fiveable.me]
- 8. youtube.com [youtube.com]
- 9. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
An In-depth Technical Guide to the Degeneracy of Rotational Energy Levels in Spherical Tops
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of the degeneracy of rotational energy levels in spherical top molecules, a fundamental concept in molecular spectroscopy with implications for molecular characterization and dynamics. The content delves into the theoretical underpinnings, the perturbations that lift this degeneracy, and the experimental methodologies employed to probe these quantum states.
Introduction to Rotational Energy Levels of Spherical Tops
Spherical top molecules, characterized by their high degree of symmetry (belonging to point groups such as Td and Oh), possess three equal moments of inertia (Ia = Ib = Ic).[1] This equality simplifies the expression for their rotational energy levels. In the rigid rotor approximation, where the molecule is treated as a rigid body with fixed bond lengths and angles, the rotational energy, E_J, is dependent on a single rotational quantum number, J, and is given by:
E_J = B J(J+1)
where B is the rotational constant, inversely proportional to the moment of inertia. This formula is identical to that for linear molecules.
A key characteristic of the rotational energy levels of spherical tops is their high degree of degeneracy. For a given rotational quantum number J, the energy level is (2J+1)²-fold degenerate in the absence of any perturbations. This high degeneracy arises from the (2J+1) possible orientations of the total angular momentum vector in space (defined by the quantum number M_J) and an additional (2J+1) degeneracy related to the orientation of the angular momentum with respect to the molecule-fixed axes.
Lifting the Degeneracy: Perturbations to the Rigid Rotor Model
The idealized picture of perfectly degenerate rotational levels is refined when considering the non-rigid nature of molecules and the coupling between rotational and vibrational motions. Two primary perturbations, centrifugal distortion and Coriolis coupling, act to lift this degeneracy, leading to a fine structure in the rovibrational spectra of spherical tops.
Centrifugal Distortion
As a molecule rotates, centrifugal forces cause a slight stretching of the bonds and a distortion of the molecular geometry. This effect is more pronounced at higher rotational speeds (i.e., higher J values). The change in the moment of inertia due to centrifugal distortion leads to a correction in the rotational energy levels. For spherical top molecules, this distortion can be anisotropic, which partially lifts the degeneracy of the rotational levels. The energy correction due to centrifugal distortion is typically expressed as a power series in J(J+1), with the leading term being:
ΔE_cd = -D [J(J+1)]²
where D is the centrifugal distortion constant.[2] For spherical tops, additional tensor terms are required to describe the splitting of the rotational levels. This splitting results in a fine structure in the observed spectra. In some cases, such as methane, centrifugal distortion can even induce a small dipole moment, allowing for the observation of a very weak pure rotational spectrum.
Coriolis Coupling
Coriolis coupling is a significant interaction in vibrating and rotating molecules, particularly for degenerate vibrational modes, which are common in spherical tops.[3] This interaction can be visualized as the coupling between the vibrational angular momentum of a degenerate vibration and the overall rotational angular momentum of the molecule. This coupling also leads to a splitting of the rovibrational energy levels. The magnitude of the splitting depends on the Coriolis coupling constant, ζ, which is specific to the interacting vibrational modes.
Experimental Determination of Rotational Energy Levels
Due to their lack of a permanent dipole moment, spherical top molecules do not exhibit a pure rotational spectrum in the microwave or far-infrared regions.[4] Therefore, their rotational energy levels are primarily investigated through rovibrational spectroscopy, where changes in both vibrational and rotational quantum numbers occur.
High-Resolution Infrared Spectroscopy
High-resolution Fourier Transform Infrared (FTIR) spectroscopy is a powerful technique for studying the rovibrational transitions of gas-phase molecules.[5][6] In this method, a broadband infrared source is passed through a sample, and the resulting interferogram is mathematically transformed to obtain a high-resolution spectrum. For spherical tops, the analysis of the fine structure within the vibrational bands allows for the determination of the rotational constant B, centrifugal distortion constants, and Coriolis coupling constants.
Experimental Protocol for High-Resolution FTIR Spectroscopy of a Gaseous Spherical Top Molecule:
-
Sample Preparation: The spherical top molecule of interest is introduced into a gas cell with appropriate windows (e.g., KBr or ZnSe) that are transparent in the infrared region of interest. The pressure of the gas is optimized to achieve sufficient absorption without significant pressure broadening of the spectral lines.
-
Spectrometer Setup: A high-resolution FTIR spectrometer is used. The instrument is typically equipped with a long-path gas cell to enhance the absorption signal for weakly absorbing species. The resolution of the spectrometer is set to a value sufficient to resolve the individual rovibrational lines (typically < 0.01 cm⁻¹).
-
Data Acquisition: The infrared beam is passed through the gas cell, and the transmitted light is detected. Multiple scans are typically co-added to improve the signal-to-noise ratio. A background spectrum of the evacuated gas cell is also recorded.
-
Data Processing: The sample interferogram is Fourier transformed to obtain the transmission spectrum. The transmission spectrum is then converted to an absorbance spectrum using the background spectrum.
-
Spectral Analysis: The positions of the individual rovibrational lines in the P, Q, and R branches of the vibrational band are accurately measured. These line positions are then fitted to a theoretical model that includes the effects of centrifugal distortion and Coriolis coupling to extract the spectroscopic constants.
High-Resolution Raman Spectroscopy
Raman spectroscopy is another crucial technique for studying the rotational and rovibrational energy levels of spherical top molecules.[7][8] This technique relies on the inelastic scattering of monochromatic light (usually from a laser). The selection rules for Raman spectroscopy are different from those for infrared absorption, providing complementary information. For a molecule to be Raman active, its polarizability must change during the vibration or rotation.
Experimental Protocol for High-Resolution Raman Spectroscopy of a Gaseous Spherical Top Molecule:
-
Sample Cell: The gaseous sample is contained in a specialized cell designed for Raman scattering experiments. The cell often has multiple windows to allow for the entry of the laser beam and the collection of the scattered light at a 90° angle.
-
Laser Source: A high-power, single-mode continuous-wave (cw) laser is used as the excitation source. The laser wavelength is chosen to avoid absorption by the sample, which could lead to fluorescence.
-
Spectrometer: The scattered light is collected and focused onto the entrance slit of a high-resolution spectrometer, typically a long-focal-length monochromator or a spectrograph equipped with a sensitive detector like a charge-coupled device (CCD).
-
Signal Collection: The Raman spectrum is recorded by scanning the spectrometer or by imaging the dispersed spectrum onto the CCD. Long integration times are often necessary due to the weakness of the Raman scattering signal.
-
Data Analysis: The rotational or rovibrational Raman spectrum is analyzed to determine the rotational constant and other spectroscopic parameters. The spacing between the lines in the pure rotational Raman spectrum is approximately 4B.
Quantitative Data
The following tables summarize the rotational and centrifugal distortion constants for some common spherical top molecules. These constants are crucial for predicting and analyzing their rovibrational spectra.
Table 1: Rotational Constants of Selected Spherical Top Molecules
| Molecule | Point Group | Rotational Constant (B₀) / cm⁻¹ | Reference |
| Methane (¹²CH₄) | Td | 5.2410356 | |
| Silane (²⁸SiH₄) | Td | 2.85906 | |
| Carbon Tetrachloride (C³⁵Cl₄) | Td | 0.0573 | |
| Sulfur Hexafluoride (³²S¹⁹F₆) | Oh | 0.091083 | [9] |
| Selenium Hexafluoride (⁸⁰Se¹⁹F₆) | Oh | 0.0811 | |
| Tellurium Hexafluoride (¹³⁰Te¹⁹F₆) | Oh | 0.0543 |
Table 2: Centrifugal Distortion Constants of Methane (¹²CH₄)
| Constant | Value / cm⁻¹ |
| D | 1.097 x 10⁻⁴ |
| H | 5.8 x 10⁻⁹ |
| L | -2.1 x 10⁻¹³ |
Visualizations
The logical relationships and workflows described in this guide can be visualized using diagrams.
Caption: Perturbations lifting the degeneracy of rotational energy levels.
Caption: Workflow for the experimental determination of spectroscopic constants.
Conclusion
The study of the degeneracy of rotational energy levels in spherical top molecules provides deep insights into molecular structure, dynamics, and the subtle interplay of quantum mechanical forces. While the rigid rotor model offers a simplified and elegant description, the fine structure observed in high-resolution rovibrational spectra reveals the importance of centrifugal distortion and Coriolis coupling. The experimental techniques of high-resolution infrared and Raman spectroscopy are indispensable tools for probing these effects and for the precise determination of molecular constants. This knowledge is fundamental for a wide range of scientific disciplines, including atmospheric science, astrophysics, and the detailed characterization of molecules relevant to drug development.
References
- 1. m.youtube.com [m.youtube.com]
- 2. davuniversity.org [davuniversity.org]
- 3. spiedigitallibrary.org [spiedigitallibrary.org]
- 4. research.cbc.osu.edu [research.cbc.osu.edu]
- 5. researchgate.net [researchgate.net]
- 6. ir.ethz.ch [ir.ethz.ch]
- 7. cdnsciencepub.com [cdnsciencepub.com]
- 8. pubs.aip.org [pubs.aip.org]
- 9. researchgate.net [researchgate.net]
An In-depth Technical Guide to Molecular Tops in Chemistry
For Researchers, Scientists, and Drug Development Professionals
Executive Summary
In the realm of physical chemistry and molecular physics, the concept of "molecular tops" is fundamental to understanding the rotational behavior of molecules. This guide provides a comprehensive overview of the classification of molecules as rigid rotors—spherical, symmetric, and asymmetric tops—based on their moments of inertia. Understanding this classification is crucial for interpreting rotational spectra, which in turn yields high-precision data on molecular geometry and electronic structure. For drug development professionals, this knowledge is instrumental in molecular modeling and designing molecules with specific shapes to interact with biological targets. This document details the theoretical underpinnings, experimental protocols for investigation (primarily microwave spectroscopy), and the significance of this classification in various scientific domains.
Introduction to Molecular Tops: The Rigid Rotor Model
The foundation of understanding the rotational motion of molecules lies in the rigid rotor approximation, which posits that a molecule can be treated as a rigid body with fixed bond lengths and angles. The rotational behavior of any rigid body is characterized by its three principal moments of inertia, denoted as
IaIbIcDiscovery and Theoretical Framework
The theoretical framework for molecular rotation is rooted in quantum mechanics. The rotational energy levels of a molecule are quantized, and transitions between these levels can be observed spectroscopically, typically in the microwave region of the electromagnetic spectrum. The Schrödinger equation for a rigid rotor yields energy levels that are dependent on the principal moments of inertia.
The general equation for a moment of inertia is:
I=∑imiri2miri-
Spherical Tops: All three moments of inertia are equal (
).Ia=Ib=Ic -
Symmetric Tops: Two of the three moments of inertia are equal. These are further divided into:
-
Asymmetric Tops: All three moments of inertia are different (
).[3]Ia=Ib=Ic -
Linear Molecules: One moment of inertia is zero (along the internuclear axis), and the other two are equal (
).Ia=0,Ib=Ic
This classification is a cornerstone of molecular spectroscopy.
Classification of Molecular Tops and Their Spectroscopic Signatures
Spherical Tops
Molecules with high symmetry, such as methane (B114726) (CH₄) and sulfur hexafluoride (SF₆), fall into this category. Due to their perfect symmetry, they possess no permanent dipole moment. Consequently, they do not exhibit a pure rotational spectrum, as there is no dipole to interact with the electromagnetic radiation.[3]
Symmetric Tops
Symmetric top molecules have one unique rotational axis and two with equivalent inertia.[3] Their rotational energy levels are described by two quantum numbers, J (total angular momentum) and K (the projection of J onto the principal axis).[1]
-
Prolate Symmetric Tops: Examples include chloromethane (B1201357) (CH₃Cl) and methyl fluoride (B91410) (CH₃F).
-
Oblate Symmetric Tops: Benzene (C₆H₆) and ammonia (B1221849) (NH₃) are classic examples.
The rotational energy for a symmetric top is given by:
E(J,K)=BJ(J+1)+(A−B)K2Asymmetric Tops
The majority of molecules are asymmetric tops, with three different moments of inertia.[4] Examples include water (H₂O) and acetone. Their rotational energy levels cannot be expressed in a simple formula, and their spectra are considerably more complex than those of symmetric tops.[3][5] However, the wealth of lines in their spectra provides a rich source of information for precise structural determination.[4]
Linear Molecules
Diatomic molecules like carbon monoxide (CO) and polyatomic linear molecules such as carbonyl sulfide (B99878) (OCS) are treated as linear rotors. Their rotational spectra are the simplest, with equally spaced lines, which allows for straightforward determination of their single moment of inertia and, consequently, their bond length(s).
Significance and Applications in Research and Drug Development
High-Precision Molecular Structure Determination
The primary application of studying molecular tops is the determination of molecular structures with extremely high precision. Rotational spectroscopy can provide bond lengths and angles to an accuracy of a thousandth of an angstrom and a tenth of a degree, respectively. This data is a critical benchmark for computational chemistry methods.
Drug Development and Molecular Recognition
In drug development, the three-dimensional shape of a molecule is paramount for its biological activity.[6] Understanding the rotational properties and the resulting molecular geometry is crucial for:
-
Ligand-Receptor Interactions: The shape complementarity between a drug molecule and its biological target is a key determinant of binding affinity.[6]
-
Computational Modeling: Accurate geometric parameters derived from rotational spectroscopy serve as a basis for molecular mechanics force fields and for validating quantum chemical calculations used in drug design.
-
Quantitative Structure-Activity Relationships (QSAR): Molecular topology and shape are used to develop QSAR models that predict the biological activity of novel compounds.[7][8][9]
Astrochemistry
Rotational spectroscopy is a powerful tool for detecting molecules in the interstellar medium. The unique spectral fingerprint of each molecule allows astronomers to identify the chemical composition of distant gas clouds, leading to discoveries of complex organic molecules in space.
Data Presentation: Rotational Properties of Representative Molecules
| Molecule | Formula | Type of Top | Iₐ (amu·Å²) | Iₑ (amu·Å²) | Iₑ (amu·Å²) |
| Methane | CH₄ | Spherical | 5.313 | 5.313 | 5.313 |
| Chloromethane | CH₃Cl | Prolate Symmetric | 5.49 | 34.1 | 34.1 |
| Benzene | C₆H₆ | Oblate Symmetric | 88.9 | 88.9 | 177.8 |
| Water | H₂O | Asymmetric | 0.615 | 1.15 | 1.765 |
| Carbonyl Sulfide | OCS | Linear | 0 | 83.0 | 83.0 |
Note: The moments of inertia are approximate and can vary slightly with isotopic substitution and vibrational state.
Experimental Protocols: Microwave Spectroscopy
Microwave spectroscopy is the primary experimental technique for studying the rotational transitions of molecules.
Methodology:
-
Sample Introduction: The gaseous sample is introduced into a long, evacuated waveguide at low pressure (a few millitorr) to minimize intermolecular collisions.
-
Microwave Radiation: A monochromatic, tunable microwave source (e.g., a klystron or a Gunn diode) is used to irradiate the sample. The frequency is swept over the desired range.
-
Detection: A detector, typically a crystal diode, is placed at the end of the waveguide. When the microwave frequency matches a rotational transition of the molecule, the molecules absorb the radiation, causing a decrease in the power reaching the detector.
-
Signal Processing: The signal from the detector is amplified and recorded as an absorption spectrum (intensity vs. frequency). To improve sensitivity, the microwave source is often frequency-modulated, and a phase-sensitive detector (lock-in amplifier) is used.
-
Analysis: The frequencies of the absorption lines are measured with high precision. By fitting these frequencies to the quantum mechanical models for the different types of tops, the rotational constants (and thus the moments of inertia) are determined. From these, the molecular geometry can be derived.
Visualizations
Caption: Classification of molecules based on moments of inertia.
Caption: Workflow for a microwave spectroscopy experiment.
Caption: Relationship between structure, inertia, and spectrum.
References
- 1. vallance.chem.ox.ac.uk [vallance.chem.ox.ac.uk]
- 2. chem.libretexts.org [chem.libretexts.org]
- 3. chem.libretexts.org [chem.libretexts.org]
- 4. web.gps.caltech.edu [web.gps.caltech.edu]
- 5. difference.wiki [difference.wiki]
- 6. Molecular shape technologies in drug discovery: methods and applications [pubmed.ncbi.nlm.nih.gov]
- 7. Latest advances in molecular topology applications for drug discovery - PubMed [pubmed.ncbi.nlm.nih.gov]
- 8. researchgate.net [researchgate.net]
- 9. nopr.niscpr.res.in [nopr.niscpr.res.in]
Methodological & Application
Application Notes and Protocols: Determination of Rotational Constants for Asymmetric Top Molecules
Audience: Researchers, scientists, and drug development professionals.
Objective: This document provides a detailed guide on the theoretical calculation and experimental determination of rotational constants for asymmetric top molecules, which are crucial for understanding molecular structure, dynamics, and intermolecular interactions.
Theoretical Framework: Understanding Asymmetric Top Rotors
A molecule is classified as an asymmetric top if its three principal moments of inertia are unique: Ia ≠ Ib ≠ Ic.[1] Most molecules fall into this category.[2] The rotational motion of such molecules is described by three rotational constants, A, B, and C, which are inversely proportional to the principal moments of inertia. By convention, they are ordered A ≥ B ≥ C, which corresponds to Ia ≤ Ib ≤ Ic, where 'a', 'b', and 'c' are the principal axes of inertia.
The rotational constants are fundamental physical properties that are directly determined by the molecule's mass distribution and geometry. They are typically expressed in units of gigahertz (GHz) or inverse centimeters (cm⁻¹). The relationship between the rotational constants and the principal moments of inertia is given by the following equations:
A=8π2IahB=8π2IbhC=8π2IchWhen expressed in frequency units (like Hz or GHz), the formula is as shown above. When expressed in wavenumbers (cm⁻¹), the speed of light, c, is included in the denominator:[3]
A=8π2cIahB=8π2cIbhC=8π2cIchHere, h is Planck's constant. The determination of these constants is essential for analyzing microwave and high-resolution infrared spectra, which in turn can yield highly precise molecular structures, including bond lengths and angles.[4][5]
Computational Protocol: Calculating Rotational Constants from Molecular Structure
This protocol outlines the steps to calculate the rotational constants of an asymmetric top molecule from its known 3D structure, often obtained from quantum chemistry calculations or crystallographic data.
2.1 Step 1: Obtain Atomic Coordinates Start with the Cartesian coordinates (xi, yi, zi) and mass (mi) for each of the N atoms in the molecule.
2.2 Step 2: Determine the Center of Mass (COM) The origin of the coordinate system must be shifted to the center of mass for the subsequent calculations. The coordinates of the COM (Xcom, Ycom, Zcom) are calculated as follows:
Xcom=M1∑i=1NmixiYcom=M1∑i=1NmiyiZcom=M1∑i=1Nmiziwhere M is the total mass of the molecule (
M=∑mixi′=xi−Xcomyi′=yi−Ycomzi′=zi−Zcom2.3 Step 3: Construct the Moment of Inertia Tensor The moment of inertia is a tensor quantity represented by a 3x3 symmetric matrix. The elements of this tensor (I) are calculated using the COM-adjusted coordinates:
i{}^2 + z'_i{}^2)Ixx=∑i=1Nmi(yi′2+zi′2){yy} = \sum_{i=1}^{N} m_i (x'i{}^2 + z'_i{}^2)Iyy=∑i=1Nmi(xi′2+zi′2)
{zz} = \sum_{i=1}^{N} m_i (x'_i{}^2 + y'_i{}^2)Izz=∑i=1Nmi(xi′2+yi′2)
The off-diagonal elements, known as products of inertia, are:
i y'_iIxy=Iyx=−∑i=1Nmixi′yi′{xz} = I_{zx} = -\sum_{i=1}^{N} m_i x'i z'_iIxz=Izx=−∑i=1Nmixi′zi′
{yz} = I_{zy} = -\sum_{i=1}^{N} m_i y'_i z'_iIyz=Izy=−∑i=1Nmiyi′zi′
The full tensor is:
I=IxxIyxIzxIxyIyyIzyIxzIyzIzz2.4 Step 4: Diagonalize the Tensor to Find Principal Moments of Inertia Diagonalizing the moment of inertia tensor yields its eigenvalues, which are the principal moments of inertia (Ia, Ib, Ic).[6] This process is equivalent to finding a new coordinate system (the principal axes) where the products of inertia are zero.[7]
P−1IP=Ia000Ib000IcThe eigenvalues Ia, Ib, and Ic are the desired principal moments of inertia.
2.5 Step 5: Convert Moments of Inertia to Rotational Constants Using the formulas from Section 1.0, convert the calculated principal moments of inertia into the rotational constants A, B, and C.
Logical Workflow for Computational Determination
Caption: Workflow for calculating rotational constants from molecular geometry.
Experimental Protocol: Determination via Microwave Spectroscopy
High-resolution rotational spectroscopy is the most precise method for determining the rotational constants of a molecule in the gas phase.[4] Microwave spectroscopy is particularly well-suited for this purpose as it directly probes transitions between rotational energy levels.[8]
3.1 Materials and Equipment
-
Volatile sample of the molecule of interest.
-
Microwave spectrometer (e.g., a cavity Fourier-transform microwave (FTMW) spectrometer or a chirped-pulse FTMW spectrometer).
-
Vacuum system.
-
Carrier gas (e.g., Argon or Neon).
-
Data acquisition and analysis software.
3.2 Experimental Procedure
-
Sample Preparation: The sample is typically seeded at a low concentration (e.g., <1%) in a carrier gas like argon. For solids or liquids, the sample is heated to produce sufficient vapor pressure.
-
Introduction into Spectrometer: The gas mixture is introduced into a high-vacuum chamber via a pulsed nozzle, creating a supersonic jet. This expansion cools the molecules to very low rotational and vibrational temperatures (~1-5 K), simplifying the resulting spectrum.
-
Microwave Excitation: A pulse of microwave radiation is directed into the chamber. If the frequency of the radiation matches a rotational transition, the molecules are coherently excited into a superposition of rotational states.
-
Data Acquisition: After the excitation pulse, the molecules emit a faint microwave signal (Free Induction Decay or FID) as they relax. This time-domain signal is detected by a sensitive receiver.
-
Signal Processing: The FID signal is digitized and then Fourier-transformed to convert it from the time domain to the frequency domain, yielding a high-resolution spectrum of transition frequencies versus intensity.
3.3 Spectral Analysis
-
Prediction: The process begins by predicting the rotational spectrum using constants derived from computational chemistry (as described in Section 2.0). This provides a starting point for identifying transitions.
-
Assignment: The complex spectrum of an asymmetric top does not have a simple pattern.[2][8] The assignment process involves matching the observed transition frequencies to specific quantum number changes (J', K'a, K'c ← J'', K''a, K''c). This is an iterative process often aided by specialized software.
-
Fitting: Once a sufficient number of transitions are assigned, their frequencies are fit to a theoretical model, typically using an effective rotational Hamiltonian like Watson's A- or S-reduced Hamiltonian.[9] This least-squares fitting process refines the values of the rotational constants (A, B, C) and also determines centrifugal distortion constants, which account for the molecule not being a perfect rigid rotor.[9]
Experimental and Data Analysis Workflow
Caption: Workflow for the experimental determination of rotational constants.
Data Summary and Presentation
The following tables summarize the key formulas and provide an example for the water molecule (H₂O), a classic asymmetric top.
Table 1: Key Formulas for Rotational Constant Calculation
| Parameter | Formula | Description |
| Center of Mass | | Calculates the x-coordinate of the center of mass. Similar formulas for Y and Z. |
| Moment of Inertia (diagonal) | | Calculates the moment of inertia about the x-axis relative to the COM. |
| Product of Inertia (off-diagonal) | | Calculates the product of inertia, which is zero in the principal axis system. |
| Rotational Constant (Frequency) | | Converts the principal moment of inertia Ib to the rotational constant B in Hz.[10] |
| Rotational Constant (Wavenumber) | | Converts the principal moment of inertia Ib to the rotational constant B in cm⁻¹.[3] |
Table 2: Example Data - Water (H₂O)
The water molecule is an important example of an asymmetric top.[4] Below are its experimentally determined ground-state rotational constants.
| Constant | Value (GHz) | Value (cm⁻¹) | Corresponding Moment of Inertia (amu·Å²) |
| A | 835.833 | 27.8806 | 0.605 |
| B | 435.345 | 14.5215 | 1.160 |
| C | 278.355 | 9.2852 | 1.815 |
Note: Values are approximate. The precise values can be determined to very high accuracy through spectroscopic fitting.[5]
References
- 1. Moment of inertia [web.chem.ox.ac.uk]
- 2. weichman.princeton.edu [weichman.princeton.edu]
- 3. fiveable.me [fiveable.me]
- 4. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 5. undergradresearch.chem.wisc.edu [undergradresearch.chem.wisc.edu]
- 6. users.math.msu.edu [users.math.msu.edu]
- 7. ae.msstate.edu [ae.msstate.edu]
- 8. chem.libretexts.org [chem.libretexts.org]
- 9. pubs.aip.org [pubs.aip.org]
- 10. CCCBDB Converting between rotational constants and moments of inertia [cccbdb.nist.gov]
Application Notes and Protocols for the Experimental Determination of Molecular Moments of Inertia
For Researchers, Scientists, and Drug Development Professionals
Introduction
The moment of inertia of a molecule is a fundamental physical property that describes its resistance to rotational acceleration about a particular axis. It is determined by the masses of the constituent atoms and their spatial arrangement, making it a crucial parameter for elucidating molecular structure, including bond lengths and angles with high precision.[1] The determination of molecular moments of inertia is pivotal in various scientific disciplines, including structural chemistry, molecular physics, and drug development, where a detailed understanding of a molecule's three-dimensional conformation is essential for predicting its interactions and activity.
This document provides detailed application notes and protocols for the three primary experimental techniques used to determine molecular moments of inertia: Microwave Spectroscopy, Rotational Raman Spectroscopy, and High-Resolution Infrared Spectroscopy.
Key Experimental Techniques
The choice of technique primarily depends on the properties of the molecule under investigation, specifically whether it possesses a permanent dipole moment.
-
Microwave (Rotational) Spectroscopy: This is a high-resolution technique applicable to molecules with a permanent electric dipole moment. It directly measures the frequencies of transitions between quantized rotational energy levels.[2][3]
-
Rotational Raman Spectroscopy: This method is suitable for non-polar molecules that lack a permanent dipole moment but have an anisotropic polarizability. It observes the rotational structure through inelastic scattering of light.[4]
-
High-Resolution Infrared (Vibration-Rotation) Spectroscopy: This technique examines the fine structure due to rotational transitions that accompany vibrational transitions. It can be applied to any molecule that has an infrared-active vibrational mode.[5]
Data Presentation: Rotational Constants and Moments of Inertia
The analysis of the spectra obtained from these techniques yields the rotational constant(s), B, of the molecule. The rotational constant is inversely proportional to the moment of inertia, I. For a diatomic or linear molecule, the relationship is given by:
I = h / (8π²Bc)
where h is Planck's constant and c is the speed of light.
Below is a summary of experimentally determined rotational constants and the corresponding moments of inertia for several common molecules.
| Molecule | Spectroscopic Technique | Rotational Constant (B) (cm⁻¹) | Moment of Inertia (I) (kg·m²) | Reference(s) |
| Hydrogen Chloride (HCl) | Infrared Spectroscopy | 10.59342 | 2.642 x 10⁻⁴⁷ | [6] |
| Carbon Monoxide (CO) | Infrared Spectroscopy | 1.92253 | 1.456 x 10⁻⁴⁶ | [7] |
| Nitrous Oxide (N₂O) | Infrared Spectroscopy | 0.41901 | 6.681 x 10⁻³⁹ | [8] |
| Carbonyl Sulfide (OCS) | Microwave Spectroscopy | 0.202864 | 1.380 x 10⁻⁴⁵ | [9] |
| Methane (CH₄) | Infrared Spectroscopy | 5.24120 | 5.342 x 10⁻⁴⁷ | [8] |
Experimental Protocols
Microwave Spectroscopy
Microwave spectroscopy offers very high resolution and is the most direct method for determining the moments of inertia for polar molecules.[2]
Objective: To obtain the pure rotational spectrum of a gaseous polar molecule and determine its rotational constant and moment of inertia.
Materials:
-
Microwave Spectrometer (comprising a microwave source, absorption cell, and detector)
-
Vacuum pump and pressure gauge
-
Sample gas (e.g., Carbonyl Sulfide, OCS)
-
Gas handling line
Protocol:
-
System Preparation:
-
Ensure the microwave spectrometer is powered on and has reached a stable operating temperature.
-
Evacuate the absorption cell and the gas handling line using the vacuum pump to a low pressure (typically < 1 mTorr) to remove any residual gases.
-
-
Sample Introduction:
-
Introduce the gaseous sample into the absorption cell through the gas handling line.
-
Carefully control the pressure of the sample gas. A low pressure (typically 10-100 mTorr) is required to minimize pressure broadening of the spectral lines.[7]
-
-
Data Acquisition:
-
Set the microwave source to sweep through the desired frequency range (e.g., 8-18 GHz).
-
The microwave radiation is passed through the absorption cell containing the sample gas.
-
The detector measures the intensity of the microwave radiation that is transmitted through the sample.
-
As the frequency is swept, the molecule will absorb radiation at specific frequencies corresponding to transitions between rotational energy levels. These absorptions will appear as dips in the transmitted intensity.
-
Record the absorption spectrum, which is a plot of absorption intensity versus frequency.
-
-
Data Analysis:
-
Identify the series of absorption lines in the spectrum. For a rigid linear molecule, these lines will be approximately equally spaced.
-
Measure the frequencies of the absorption lines. The frequency difference between adjacent lines in the pure rotational spectrum of a linear molecule is approximately 2B (where B is the rotational constant in frequency units).
-
Calculate the average spacing between the lines to determine the value of 2B.
-
Convert the rotational constant B from frequency units (e.g., GHz) to wavenumbers (cm⁻¹) if necessary.
-
Calculate the moment of inertia (I) using the formula: I = h / (8π²B).
-
Rotational Raman Spectroscopy
This technique is essential for determining the moments of inertia of non-polar molecules.
Objective: To obtain the pure rotational Raman spectrum of a gaseous non-polar molecule and determine its rotational constant and moment of inertia.
Materials:
-
Raman Spectrometer (with a high-resolution spectrograph)
-
Laser source (e.g., Argon ion laser)
-
Gas sample cell
-
Sample gas (e.g., N₂, O₂)
Protocol:
-
Instrument Setup:
-
Align the laser beam to pass through the center of the gas sample cell.
-
Position the collection optics at a 90° angle to the incident laser beam to collect the scattered light.
-
-
Sample Preparation:
-
Fill the gas sample cell with the sample gas to the desired pressure (typically atmospheric pressure).
-
-
Data Acquisition:
-
Irradiate the sample with the monochromatic laser beam.
-
Collect the scattered light and direct it into the high-resolution spectrograph.
-
Record the Raman spectrum, which will show a strong central line at the laser frequency (Rayleigh scattering) and a series of weaker lines on either side (Raman scattering).[10]
-
The lines on the low-frequency side are the Stokes lines, and the lines on the high-frequency side are the anti-Stokes lines.
-
-
Data Analysis:
-
Measure the Raman shift (in wavenumbers, cm⁻¹) of each of the Stokes and anti-Stokes lines relative to the Rayleigh line.[11]
-
For a linear molecule, the selection rule for rotational Raman transitions is ΔJ = ±2.[12]
-
The spacing between the Rayleigh line and the first Stokes/anti-Stokes line is 6B, and the spacing between subsequent rotational lines is 4B.
-
Assign the rotational quantum numbers (J) to the observed transitions.
-
Plot the Raman shift of the lines against the appropriate function of J. The slope of this plot will be related to the rotational constant B.
-
Calculate the rotational constant B.
-
Calculate the moment of inertia (I) using the rotational constant.
-
High-Resolution Infrared Spectroscopy
This method is used to study the rotational fine structure of vibrational bands.
Objective: To obtain a high-resolution vibration-rotation spectrum of a gaseous molecule and determine its rotational constants and moment of inertia.
Materials:
-
High-resolution Fourier-Transform Infrared (FT-IR) Spectrometer
-
Gas cell with IR-transparent windows (e.g., KBr, NaCl)
-
Vacuum pump and pressure gauge
-
Sample gas (e.g., HCl, CO)
Protocol:
-
Spectrometer Preparation:
-
Purge the spectrometer with a dry, CO₂-free gas (e.g., nitrogen) to minimize atmospheric interference.
-
Set the spectrometer to a high resolution, typically 0.5 cm⁻¹ or better.[13]
-
-
Sample Preparation:
-
Evacuate the gas cell using a vacuum pump.
-
Introduce the sample gas into the cell to a pressure that gives optimal absorbance (typically a few hundred Torr).
-
-
Data Acquisition:
-
Place the gas cell in the sample compartment of the FT-IR spectrometer.
-
Acquire a background spectrum of the empty (evacuated) cell.
-
Acquire the sample spectrum. The spectrometer will automatically ratio the sample spectrum to the background spectrum to produce an absorbance or transmittance spectrum.
-
The resulting spectrum will show one or more vibrational bands, each with a series of sharp rotational lines.
-
-
Data Analysis:
-
Identify the P-branch (lower frequency) and R-branch (higher frequency) of a vibrational band. For linear molecules, a Q-branch may be absent.[5]
-
Assign the rotational quantum number J to each line in the P and R branches.
-
The spacing between adjacent rotational lines is approximately 2B.
-
Use the method of combination differences to determine the rotational constants for both the ground (B₀) and excited (B₁) vibrational states more accurately.
-
From the rotational constants, calculate the corresponding moments of inertia.
-
References
- 1. faculty.fiu.edu [faculty.fiu.edu]
- 2. chem.libretexts.org [chem.libretexts.org]
- 3. chem.libretexts.org [chem.libretexts.org]
- 4. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 5. m.youtube.com [m.youtube.com]
- 6. "Analysis of rovibrational spectra of diatomic molecules" by Kurt W. Kolasinski [digitalcommons.wcupa.edu]
- 7. files01.core.ac.uk [files01.core.ac.uk]
- 8. Solved 1. The moment of inertia of a CH4 molecule is 5.27 | Chegg.com [chegg.com]
- 9. youtube.com [youtube.com]
- 10. kuvempu.ac.in [kuvempu.ac.in]
- 11. astro1.panet.utoledo.edu [astro1.panet.utoledo.edu]
- 12. phys.ubbcluj.ro [phys.ubbcluj.ro]
- 13. Infrared Spectroscopy on Gases | The Infrared and Raman Discussion Group [irdg.org]
Application Notes and Protocols for Microwave Spectroscopy of Symmetric Top Molecules
For Researchers, Scientists, and Drug Development Professionals
Introduction
Microwave spectroscopy is a high-resolution technique that probes the quantized rotational energy levels of molecules in the gas phase.[1][2] By measuring the frequencies of rotational transitions, highly precise information about a molecule's structure, including bond lengths, bond angles, and dipole moments, can be determined.[3] This application note provides a detailed protocol for the study of symmetric top molecules using Fourier Transform Microwave (FTMW) spectroscopy. Symmetric top molecules, which have two of their three principal moments of inertia equal, serve as an important class of molecules for spectroscopic investigation due to their relatively simple and predictable rotational spectra.[4] Examples include molecules with a C3 or higher axis of rotational symmetry, such as methyl chloride (CH₃Cl) and fluoroform (CHF₃).[3][5]
Principle of the Technique
Microwave spectroscopy relies on the absorption of microwave radiation by a molecule with a permanent electric dipole moment, causing a transition between rotational energy levels.[6] For a symmetric top molecule, the rotational energy levels are characterized by two quantum numbers, J and K. J represents the total angular momentum of the molecule, while K is the projection of the total angular momentum onto the principal symmetry axis.
The selection rules for rotational transitions in symmetric top molecules are:
-
ΔJ = ±1 (for absorption, ΔJ = +1)
-
ΔK = 0
This results in a spectrum consisting of a series of lines, where each J → J+1 transition is composed of several closely spaced K components. The frequency of these transitions can be related to the rotational constants of the molecule, which are inversely proportional to the moments of inertia.
Experimental Protocol: Fourier Transform Microwave (FTMW) Spectroscopy of a Gaseous Symmetric Top Molecule
This protocol outlines the general steps for acquiring the microwave spectrum of a gaseous symmetric top molecule, such as methyl chloride, using a pulsed-jet FTMW spectrometer.
1. Sample Preparation:
-
For volatile liquids or gases like methyl chloride, the sample is typically a mixture of a small percentage (e.g., 1%) of the sample gas in a carrier gas, such as argon or neon.[4]
-
The gas mixture is prepared in a high-pressure cylinder. The concentration of the sample gas can be adjusted to optimize the signal intensity.
-
For solid samples, they must be heated to produce a sufficient vapor pressure to be entrained in the carrier gas.
2. Experimental Setup and Data Acquisition:
A typical FTMW spectrometer consists of a vacuum chamber, a pulsed nozzle for introducing the sample, a microwave source, a Fabry-Pérot cavity, and a sensitive detector.[7]
-
Sample Introduction: The gas mixture is introduced into the evacuated Fabry-Pérot cavity through a pulsed nozzle. This creates a supersonic expansion, which cools the molecules to very low rotational and vibrational temperatures (a few Kelvin).[7] This cooling simplifies the spectrum by populating only the lowest energy levels.
-
Microwave Pulse: A short, high-power microwave pulse is introduced into the cavity. If the frequency of the microwave pulse is resonant with a rotational transition of the molecules, it will induce a macroscopic polarization in the gas sample.[7]
-
Detection of Free Induction Decay (FID): After the microwave pulse, the coherently rotating molecules emit a faint microwave signal, known as the Free Induction Decay (FID). This decaying signal is detected by a sensitive receiver.[7]
-
Signal Averaging: The FID signal from a single gas pulse is very weak. Therefore, the signal is typically averaged over many thousands of pulses to improve the signal-to-noise ratio.
3. Data Processing and Analysis:
-
Fourier Transformation: The time-domain FID signal is converted into a frequency-domain spectrum by applying a Fourier transform.[7] This results in a spectrum of absorption intensity versus frequency.
-
Spectral Assignment: The observed peaks in the spectrum are assigned to specific rotational transitions (i.e., specific J and K quantum numbers). This is often done by comparing the experimental spectrum to a predicted spectrum based on an initial estimate of the rotational constants.
-
Spectral Fitting: The frequencies of the assigned transitions are then fitted to a model Hamiltonian using a least-squares fitting program. This fitting process yields precise values for the rotational constants (A, B, C) and, if the resolution is high enough, centrifugal distortion constants (e.g., DJ, DJK).[8]
-
Stark Effect Measurements for Dipole Moment Determination: To determine the electric dipole moment, a static electric field (Stark field) is applied across the sample. This field splits the rotational energy levels, and the magnitude of this splitting is proportional to the dipole moment.[3] By measuring the frequency shifts of the rotational transitions as a function of the applied electric field, the dipole moment can be accurately determined.
Data Presentation: Spectroscopic Constants of Symmetric Top Molecules
The following table summarizes the experimentally determined spectroscopic constants for two common symmetric top molecules, methyl chloride (CH₃Cl) and fluoroform (CHF₃).
| Molecule | Rotational Constant A (MHz) | Rotational Constant B (MHz) | DJ (kHz) | DJK (kHz) | Dipole Moment (Debye) |
| CH₃⁵Cl | 157330.1 | 13292.9 | 18.2 | 199.8 | 1.892 |
| CHF₃ | 10348 | 10348 | - | - | 1.645 |
Data for CH₃Cl from the CCCBDB database and a research paper on its rotational and centrifugal distortion constants.[8] Data for CHF₃ from a study on rotational properties of interacting polar molecules.[9]
Visualizations
References
- 1. researchgate.net [researchgate.net]
- 2. researchgate.net [researchgate.net]
- 3. faculty.fiu.edu [faculty.fiu.edu]
- 4. Fourier-transform microwave spectroscopy of the CCCCl radical - PubMed [pubmed.ncbi.nlm.nih.gov]
- 5. Fluoroform - Wikipedia [en.wikipedia.org]
- 6. youtube.com [youtube.com]
- 7. Dr. Jäger’s Group Homepage - FTMW Spectroscopy [chem.ualberta.ca]
- 8. researchgate.net [researchgate.net]
- 9. researchgate.net [researchgate.net]
Unveiling Molecular Choreography: A Guide to Studying Molecular Rotation with Raman Spectroscopy
For Researchers, Scientists, and Drug Development Professionals
Application Note RA-001
Introduction
Raman spectroscopy, a non-destructive light-scattering technique, offers a powerful analytical window into the rotational motion of molecules. By probing the quantized rotational energy levels, researchers can elucidate fundamental molecular properties such as bond lengths and moments of inertia with high precision. This information is invaluable across various scientific disciplines, from fundamental chemical physics to the practicalities of pharmaceutical development, where understanding the precise three-dimensional structure of an active pharmaceutical ingredient (API) is paramount. This document provides a detailed overview of the principles, experimental protocols, and data analysis workflows for studying molecular rotation using Raman spectroscopy, with a particular focus on applications relevant to pharmaceutical sciences.
Principles of Rotational Raman Spectroscopy
Raman spectroscopy is predicated on the inelastic scattering of photons by molecules. When a monochromatic light source, typically a laser, interacts with a molecule, most of the scattered light (Rayleigh scattering) has the same frequency as the incident light. However, a small fraction of the light is scattered at a different frequency, a phenomenon known as the Raman effect. This frequency shift corresponds to the energy difference between the initial and final rotational or vibrational states of the molecule.
For a molecule to exhibit a rotational Raman spectrum, its polarizability must be anisotropic, meaning the ease with which its electron cloud can be distorted by an electric field depends on the molecule's orientation.[1] This condition allows for coupling between the incident light and the rotational motion of the molecule. Consequently, linear and symmetric top molecules are typically rotationally Raman active, while spherical top molecules are not.[2]
The selection rule for pure rotational Raman transitions in linear molecules is ΔJ = 0, ±2, where J is the rotational quantum number.[3]
-
ΔJ = 0 corresponds to Rayleigh scattering, where there is no change in rotational energy.
-
ΔJ = +2 results in Stokes lines, where the molecule is excited to a higher rotational energy level, and the scattered photon has lower energy (longer wavelength) than the incident photon.
-
ΔJ = -2 gives rise to anti-Stokes lines, where the molecule transitions to a lower rotational energy level, and the scattered photon has higher energy (shorter wavelength).
The energy of the rotational levels for a rigid diatomic molecule is given by:
E_J = B * J(J+1)
where B is the rotational constant, which is inversely proportional to the molecule's moment of inertia (I). The Raman shift (Δν) for a transition from an initial state J is therefore:
Δν = E_{J+2} - E_J = B[(J+2)(J+3) - J(J+1)] = 2B(2J+3)
This relationship allows for the determination of the rotational constant B from the spacing of the lines in the rotational Raman spectrum. From the rotational constant, the moment of inertia (I) and subsequently the internuclear distance or bond length (r) can be calculated.
Experimental Protocols
A successful rotational Raman spectroscopy experiment requires careful attention to the experimental setup, sample preparation, and data acquisition parameters.
I. Instrumentation and Setup
A typical experimental setup for rotational Raman spectroscopy of gases is depicted below.
Caption: Diagram of a typical experimental setup for rotational Raman spectroscopy.
Key Components:
-
Laser Source: A stable, monochromatic laser is essential. Argon ion lasers (e.g., 488.0 nm or 514.5 nm) are commonly used.[4]
-
Sample Cell: For gaseous samples, a sealed cell with optically transparent windows is required. The cell can be filled with the gas of interest to a desired pressure.
-
Collection Optics: Lenses are used to focus the laser beam into the sample cell and to collect the scattered light, typically at a 90° angle to the incident beam to minimize stray light.
-
Rayleigh Rejection Filter: A notch or long-pass filter is crucial to attenuate the intense Rayleigh scattered light, which would otherwise overwhelm the weak Raman signal.[5]
-
Spectrometer: A high-resolution spectrometer is necessary to resolve the closely spaced rotational lines.
-
Detector: A sensitive detector, such as a charge-coupled device (CCD) camera, is used to record the dispersed Raman spectrum.
II. Instrument Calibration
Accurate calibration of the Raman spectrometer is critical for obtaining reliable data.
-
Wavelength Axis Calibration:
-
Use a standard calibration lamp (e.g., neon or argon) with known emission lines to calibrate the wavelength axis of the spectrometer.[6]
-
Alternatively, a standard material with well-characterized Raman peaks (e.g., polystyrene) can be used.[7]
-
This calibration ensures that the measured Raman shifts are accurate.
-
-
Intensity Axis Calibration:
-
Use a calibrated light source or a standard material with a known Raman cross-section to correct for the wavelength-dependent response of the spectrometer and detector.[6]
-
III. Sample Preparation
For Gaseous Samples (e.g., N₂, O₂, CO₂):
-
Ensure the gas sample cell is clean and leak-proof.
-
Evacuate the cell to remove any residual air or contaminants.
-
Fill the cell with the gas sample to the desired pressure. For atmospheric gases like N₂ and O₂, ambient air can be used.[8]
For Pharmaceutical Samples (Polymorph and API Analysis):
-
Solids: Samples are typically analyzed as powders or crystalline solids. Minimal sample preparation is often required, which is a significant advantage as it reduces the risk of inducing polymorphic transformations.[9] The sample can be placed on a microscope slide or in a sample holder.
-
Solutions: If the API is in solution, it can be analyzed directly in a cuvette. The solvent should have a weak Raman signal in the region of interest. Water is a weak Raman scatterer, making it a suitable solvent for many pharmaceutical applications.[10]
IV. Data Acquisition
-
Laser Power: Use sufficient laser power to obtain a good signal-to-noise ratio, but avoid sample degradation, especially for sensitive pharmaceutical compounds.
-
Integration Time: The time the detector collects photons for a single spectrum. Longer integration times improve the signal-to-noise ratio.
-
Number of Accumulations: Averaging multiple spectra can further improve the signal quality.
-
Spectral Range: Set the spectrometer to acquire data in the region where the rotational Raman lines are expected.
Data Presentation and Analysis
The analysis of rotational Raman spectra involves several key steps to extract meaningful molecular parameters.
Caption: A step-by-step workflow for analyzing rotational Raman spectra.
I. Spectral Processing
-
Wavenumber Conversion: Convert the raw spectral data from wavelength (nm) to Raman shift in wavenumbers (cm⁻¹).[11]
-
Baseline Correction: Remove any broad background signal from the spectrum.
-
Peak Identification: Identify the positions of the Stokes and anti-Stokes rotational lines.
II. Determination of Molecular Constants
-
Assign Transitions: Assign the rotational quantum number (J) to each observed line in the Stokes and anti-Stokes branches.
-
Calculate Rotational Constant (B): The separation between adjacent Stokes lines (or anti-Stokes lines) is approximately 4B. By measuring the positions of the lines, the rotational constant B can be determined accurately.[12]
-
Calculate Moment of Inertia (I): The moment of inertia is calculated from the rotational constant using the formula: I = h / (8π²cB), where h is Planck's constant and c is the speed of light.
-
Calculate Bond Length (r): For a diatomic molecule, the bond length is calculated from the moment of inertia using: r = √(I/μ), where μ is the reduced mass of the molecule.
Quantitative Data Summary
The following table summarizes rotational constants and bond lengths for some common diatomic molecules determined by Raman spectroscopy.
| Molecule | Rotational Constant (B₀) (cm⁻¹) | Bond Length (r₀) (Å) | Reference |
| N₂ | 1.98957 | 1.1001 | [4] |
| O₂ | 1.43767 | 1.2108 | [4] |
| CO₂ | 0.39021 | 1.1621 (C=O) | [9] |
| H₂ | 60.853 | 0.7414 | [12] |
Applications in Drug Development
While the study of rotational spectra of small gas-phase molecules provides fundamental insights, the principles of Raman spectroscopy are highly applicable in the pharmaceutical industry, particularly in the solid-state characterization of APIs.
I. Polymorph Identification and Analysis
Polymorphism is the ability of a solid material to exist in multiple crystalline forms. Different polymorphs of an API can have different physical properties, including solubility, stability, and bioavailability, which can significantly impact the drug's efficacy and safety.[13] Raman spectroscopy is a powerful tool for identifying and quantifying polymorphs.
-
Principle: Different crystal lattices and molecular conformations in polymorphs lead to distinct vibrational modes, resulting in unique Raman spectra that act as "fingerprints" for each form.[14] Low-frequency Raman spectroscopy (10-200 cm⁻¹) is particularly sensitive to lattice vibrations and can provide clear discrimination between polymorphs.[15]
-
Protocol:
-
Obtain reference Raman spectra for each known polymorph of the API.
-
Acquire the Raman spectrum of the unknown sample.
-
Compare the sample spectrum to the reference spectra to identify the polymorphic form(s) present.
-
Quantitative analysis of mixtures of polymorphs can be performed by creating calibration models based on the intensities of characteristic Raman bands.[6]
-
Caption: Logical workflow for identifying and quantifying polymorphs using Raman spectroscopy.
II. Characterization of Active Pharmaceutical Ingredients (APIs)
Raman spectroscopy is used for the chemical identification and structural characterization of APIs.[16] It can confirm the identity of raw materials, intermediates, and the final product, ensuring the correct molecular structure. The technique's high chemical specificity allows for the differentiation of closely related molecules.
Conclusion
Raman spectroscopy is a versatile and powerful technique for studying molecular rotation, providing fundamental insights into molecular structure. The detailed protocols and data analysis workflows presented here offer a guide for researchers to effectively utilize this method. Furthermore, the application of Raman spectroscopy extends into the critical area of pharmaceutical development, where it plays a vital role in ensuring the quality, safety, and efficacy of drug products through the characterization of polymorphs and APIs. Its non-destructive nature and minimal sample preparation requirements make it an invaluable tool in the modern analytical laboratory.
References
- 1. researchgate.net [researchgate.net]
- 2. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 3. phys.ubbcluj.ro [phys.ubbcluj.ro]
- 4. Absolute rotational Raman cross sections for N2, O2, and CO2 | Semantic Scholar [semanticscholar.org]
- 5. alfatestlab.com [alfatestlab.com]
- 6. [PDF] Polymorph Characterization of Active Pharmaceutical Ingredients (APIs) Using Low-Frequency Raman Spectroscopy | Semantic Scholar [semanticscholar.org]
- 7. researchgate.net [researchgate.net]
- 8. pubs.acs.org [pubs.acs.org]
- 9. cefrc.princeton.edu [cefrc.princeton.edu]
- 10. Raman Shift Calculator | Photon etc. [photonetc.com]
- 11. Rotational and Vibrational Raman spectra – Atomic, Molecular and Laser Spectroscopy [ebooks.inflibnet.ac.in]
- 12. coherent.com [coherent.com]
- 13. Polymorph Discrimination using Low Wavenumber Raman Spectroscopy - PMC [pmc.ncbi.nlm.nih.gov]
- 14. spectroscopyonline.com [spectroscopyonline.com]
- 15. researchgate.net [researchgate.net]
- 16. europeanpharmaceuticalreview.com [europeanpharmaceuticalreview.com]
Application Notes and Protocols for Rotational Spectroscopy in Astrophysics
Introduction
Rotational spectroscopy is a high-resolution spectroscopic technique that probes the quantized rotational energy levels of molecules in the gas phase.[1][2][3] In astrophysics, it serves as a powerful tool for the chemical and physical characterization of celestial objects, including the interstellar medium (ISM), circumstellar envelopes, and comets.[1][2] By detecting and analyzing the rotational spectra of molecules, astronomers can identify the chemical composition of these environments, determine physical parameters such as temperature and density, and investigate the complex chemical processes that lead to the formation of stars, planets, and potentially, the building blocks of life.[4][5][6]
The underlying principle of rotational spectroscopy is that molecules with a permanent dipole moment can absorb and emit photons at specific frequencies corresponding to transitions between their rotational energy levels.[7][8] These transition frequencies are unique to each molecule, creating a distinct "fingerprint" that allows for its unambiguous identification.[9][10]
This document provides detailed application notes and protocols for the use of rotational spectroscopy in astrophysical research, aimed at researchers, scientists, and professionals in related fields.
Application Note 1: Identification of New Interstellar Molecules
Scientific Objective
To identify previously undetected molecules in the interstellar medium, thereby expanding our understanding of interstellar chemistry and the inventory of molecules available for star and planet formation.
Background
The interstellar medium is a rich reservoir of diverse molecules, many of which are highly reactive and cannot be easily studied in terrestrial laboratories.[11] Rotational spectroscopy, through radio astronomy, is the primary method for their detection.[5] The process involves a synergistic approach between laboratory spectroscopy and astronomical observation. First, the rotational spectrum of a candidate molecule is measured or predicted. Then, radio telescopes are used to search for the corresponding spectral lines in astrophysical sources. A recent example is the interstellar detection of 2-methoxyethanol.[9]
Experimental Workflow
The workflow for identifying a new interstellar molecule can be broken down into several key stages:
-
Target Molecule Selection: Promising candidate molecules are often suggested by chemical models of interstellar environments or through techniques like machine learning that predict plausible interstellar species.[9]
-
Laboratory Spectroscopy: The rotational spectrum of the target molecule is measured in the laboratory to determine its precise transition frequencies.[10][12]
-
Astronomical Observation: A radio telescope, such as the Atacama Large Millimeter/submillimeter Array (ALMA) or the Green Bank Telescope (GBT), is used to observe a celestial source where the molecule is likely to be present.
-
Data Analysis: The observational data is processed and analyzed to identify spectral lines that match the laboratory-measured frequencies of the target molecule.
-
Confirmation and Characterization: A secure detection requires the observation of multiple rotational transitions of the molecule.[9] Once confirmed, the line profiles and intensities can be used to derive physical parameters like column density and excitation temperature.[9]
Logical Workflow for Molecular Identification
References
- 1. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 2. uomustansiriyah.edu.iq [uomustansiriyah.edu.iq]
- 3. info.ifpan.edu.pl [info.ifpan.edu.pl]
- 4. Astrochemistry and Intramolecular Dynamics through Rotational Spectroscopy | JILA - Exploring the Frontiers of Physics [jila.colorado.edu]
- 5. prl.res.in [prl.res.in]
- 6. m.youtube.com [m.youtube.com]
- 7. Detection of Interstellar Molecules [sas.upenn.edu]
- 8. chem.libretexts.org [chem.libretexts.org]
- 9. Researchers detect a new molecule in space – MIT Department of Chemistry [chemistry.mit.edu]
- 10. youtube.com [youtube.com]
- 11. Hunting for interstellar molecules: rotational spectra of reactive species - PubMed [pubmed.ncbi.nlm.nih.gov]
- 12. Astrochemistry — Rotational and Computational Spectroscopy — Department of Chemistry "Giacomo Ciamician" [site.unibo.it]
Application Notes and Protocols for Assigning Quantum Numbers to Rotational Transitions
Audience: Researchers, scientists, and drug development professionals.
Introduction to Rotational Spectroscopy
Rotational spectroscopy is a high-resolution analytical technique that probes the quantized rotational energy levels of molecules in the gas phase.[1][2][3] By measuring the frequencies of transitions between these levels, typically in the microwave region of the electromagnetic spectrum, one can determine the molecule's moments of inertia with exceptional precision.[1][4] From these moments of inertia, highly accurate molecular structures, including bond lengths and angles, can be elucidated.[1][4] A key requirement for a molecule to exhibit a pure rotational spectrum is the possession of a permanent electric dipole moment.[2][5]
In recent years, advancements in chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy, commercially available as Molecular Rotational Resonance (MRR) spectroscopy, have significantly enhanced the capabilities and accessibility of this technique.[6] MRR spectroscopy offers unambiguous structural characterization of molecules, including isomers and conformers, often within complex mixtures without the need for prior separation.[6] This has profound implications for the pharmaceutical industry, accelerating drug development through rapid and precise analysis of active pharmaceutical ingredients (APIs), impurities, and reaction products.[6][7][8]
Theoretical Principles
The rotational energy levels of a molecule are quantized and, for a rigid diatomic or linear molecule, are described by the following equation:
EJ = B * J(J+1)
where:
-
EJ is the energy of the rotational level.
-
B is the rotational constant, which is inversely proportional to the molecule's moment of inertia (I).[5]
-
J is the rotational quantum number, which can take integer values (0, 1, 2, ...).[2][9]
The moment of inertia is determined by the masses of the atoms and their arrangement in space. For a diatomic molecule, it is given by I = μr2, where μ is the reduced mass and r is the bond length.
Transitions between rotational energy levels are governed by selection rules. For most molecules, the selection rule for absorption or emission of a single photon is:
This means that transitions occur between adjacent energy levels, leading to a characteristic pattern of nearly equally spaced lines in the spectrum of a diatomic molecule. The frequency of these transitions is approximately 2B(J+1) for a transition from level J to J+1.
For more complex molecules, which are classified as symmetric tops, spherical tops, or asymmetric tops based on their moments of inertia, the rotational energy levels and spectra are more intricate.[1][10] Asymmetric tops, which have three different moments of inertia, exhibit the most complex spectra.[6][10]
Experimental Protocol: Molecular Rotational Resonance (MRR) Spectroscopy
This protocol outlines the general steps for acquiring a rotational spectrum using a CP-FTMW (MRR) spectrometer.
3.1. Sample Preparation and Introduction
-
Solid Samples: Place a small amount of the solid sample (typically a few milligrams) in a sample holder. The sample will be heated to generate a sufficient vapor pressure for introduction into the spectrometer.
-
Liquid Samples: Introduce a small volume of the liquid sample into a sample vial. A carrier gas (e.g., neon, argon) is typically bubbled through the liquid to carry the vapor into the spectrometer.
-
Gaseous Samples: Introduce the gas directly into the spectrometer's vacuum chamber through a precision leak valve.
3.2. Instrument Setup and Data Acquisition
-
Vacuum: Evacuate the sample chamber to a high vacuum (typically 10-6 to 10-8 torr) to minimize collisions between molecules.
-
Molecular Beam Generation: Introduce the vaporized sample into the vacuum chamber through a pulsed nozzle. This creates a supersonic expansion, which cools the molecules to very low rotational and vibrational temperatures (a few Kelvin). This cooling simplifies the spectrum by populating only the lowest energy levels.
-
Microwave Excitation: A short, high-power pulse of microwave radiation (the "chirp") is broadcast into the chamber. This pulse rapidly sweeps a range of frequencies, exciting a broad range of rotational transitions simultaneously.
-
Free Induction Decay (FID) Detection: After the excitation pulse, the coherently rotating molecules emit a faint microwave signal known as the Free Induction Decay (FID). This signal is detected by a sensitive antenna.
-
Signal Averaging: The FID is very weak, so many pulses are repeated, and the resulting FIDs are averaged to improve the signal-to-noise ratio.
3.3. Data Processing
-
Fourier Transformation: The time-domain FID signal is converted into a frequency-domain spectrum by applying a Fourier transform. This results in a spectrum of signal intensity versus frequency.
-
Peak Picking: The frequencies of the rotational transitions are precisely determined by identifying the peaks in the spectrum.
Protocol for Assigning Quantum Numbers to Rotational Transitions
Assigning the correct quantum numbers to the observed transitions is a critical step in the analysis of a rotational spectrum. This process typically involves a combination of pattern recognition, theoretical calculations, and specialized software.
4.1. Initial Spectral Prediction (Ab Initio Calculations)
-
Computational Chemistry: Before analyzing the experimental spectrum, perform quantum chemical calculations (e.g., using density functional theory (DFT) or more advanced methods) to predict the molecule's geometry, rotational constants, and, consequently, its rotational spectrum.[11] This provides a theoretical starting point for the assignment.
-
Software: Use computational chemistry software packages like Gaussian, ORCA, or Q-Chem for these calculations.
4.2. Spectral Analysis and Assignment
-
Pattern Recognition (for simpler spectra): For linear molecules and symmetric tops, look for characteristic patterns of lines. For linear molecules, this will be a series of lines with nearly equal spacing.
-
Software-Assisted Assignment (for complex spectra): For asymmetric tops, the spectra are often too dense and complex for manual assignment.[6] Use specialized software for spectral analysis and fitting, such as:
-
PGOPHER: A widely used program for simulating and fitting rotational, vibrational, and electronic spectra.[7][8][12]
-
SPFIT/SPCAT: A suite of programs for fitting and predicting rotational spectra.[13]
-
PySpecTools: A Python library that provides a wrapper for SPFIT/SPCAT and other tools for rotational spectroscopy analysis.[13]
-
4.3. The Iterative Fitting Process (using software like PGOPHER)
-
Initial Simulation: Load the experimental spectrum into the software and generate an initial simulation based on the ab initio calculated rotational constants.
-
Tentative Assignments: Identify a few low-J transitions in the experimental spectrum that appear to match the simulation. Assign the corresponding quantum numbers to these transitions.
-
Least-Squares Fitting: Perform a least-squares fit of the assigned transitions. The software will adjust the rotational constants and other spectroscopic parameters (like centrifugal distortion constants) to minimize the difference between the observed and calculated transition frequencies.[7][11]
-
Refine and Extend Assignments: Use the newly fitted constants to predict the frequencies of other transitions. Look for these predicted transitions in the experimental spectrum and assign them.
-
Iterate: Repeat the fitting and assignment process, gradually including more transitions. This iterative process refines the spectroscopic constants and confirms the assignments.
-
Final Fit: Once a sufficient number of transitions have been assigned with a good fit (low root-mean-square error), the final set of spectroscopic constants is obtained.
Data Presentation
The primary results from the analysis of a rotational spectrum are the spectroscopic constants. These are typically presented in a tabular format, along with the derived structural parameters.
Table 1: Spectroscopic Constants and Derived Parameters for Carbonyl Sulfide (OCS)
| Parameter | Value | Unit |
| Rotational Constant (B) | 6081.492 | MHz |
| Centrifugal Distortion (D) | 1.301 | kHz |
| Moment of Inertia (I) | 83.095 | amu Ų |
| C=O Bond Length | 1.160 | Å |
| C=S Bond Length | 1.561 | Å |
Table 2: Rotational Constants for Isomers of a Pharmaceutical Precursor
| Isomer | A (MHz) | B (MHz) | C (MHz) |
| Isomer 1 | 2453.12 | 1102.45 | 987.65 |
| Isomer 2 | 2678.98 | 1054.78 | 954.32 |
Mandatory Visualizations
Experimental and Data Analysis Workflow
Caption: Workflow for molecular structure determination using MRR spectroscopy.
Logical Relationships in Spectral Assignment
Caption: Logical workflow for the assignment of rotational quantum numbers.
Applications in Drug Development
The high precision and specificity of MRR spectroscopy make it a valuable tool in the pharmaceutical industry.
-
Structural Verification: Unambiguously confirm the chemical structure of newly synthesized APIs, including the correct isomeric form.
-
Impurity Analysis: Identify and quantify isomeric and structural impurities in drug substances and raw materials, which is critical for safety and efficacy.[7]
-
Chiral Analysis: Determine the enantiomeric excess of chiral molecules, often without the need for chiral chromatography.
-
Process Analytical Technology (PAT): Enable real-time, in-situ monitoring of chemical reactions to optimize reaction conditions, yields, and purity.[6][8]
-
Residual Solvent Analysis: Detect and quantify residual solvents in pharmaceutical products, ensuring compliance with regulatory standards.[8][14]
By providing definitive structural information early in the development process, rotational spectroscopy can help de-risk drug candidates, streamline analytical workflows, and ultimately accelerate the delivery of new medicines.
References
- 1. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 2. scribd.com [scribd.com]
- 3. chem.libretexts.org [chem.libretexts.org]
- 4. uomustansiriyah.edu.iq [uomustansiriyah.edu.iq]
- 5. chemtube3d.com [chemtube3d.com]
- 6. SPIN [spin.astro.uni-koeln.de]
- 7. Walk-through of Simulating and Fitting a Simple Spectrum [pgopher.chm.bris.ac.uk]
- 8. meetings.iac.es [meetings.iac.es]
- 9. academic.oup.com [academic.oup.com]
- 10. chem.libretexts.org [chem.libretexts.org]
- 11. Molecular Structure from Rotational Spectra [hyperphysics.phy-astr.gsu.edu]
- 12. PGOPHER [pgopher.chm.bris.ac.uk]
- 13. GitHub - laserkelvin/PySpecTools: Routines for rotational spectroscopy analysis written in Python 3 [github.com]
- 14. pgopher.chm.bris.ac.uk [pgopher.chm.bris.ac.uk]
Application Notes and Protocols for Analyzing Complex Rotational Spectra
For Researchers, Scientists, and Drug Development Professionals
Introduction
Rotational spectroscopy is a high-resolution analytical technique that provides exquisitely detailed information about the structure and dynamics of molecules in the gas phase.[1][2] By probing the quantized rotational energy levels of molecules, it is possible to determine molecular geometries, identify different conformers, and even distinguish between enantiomers.[3][4] However, the spectra of large, flexible molecules or complex mixtures can be incredibly dense and challenging to analyze. This document outlines advanced techniques and protocols for the confident analysis of such complex rotational spectra, with a focus on modern experimental and computational methods.
Chirped-Pulse Fourier Transform Microwave (CP-FTMW) Spectroscopy
Chirped-Pulse Fourier Transform Microwave (CP-FTMW) spectroscopy is a powerful technique for the rapid acquisition of broadband rotational spectra.[3] This method utilizes a short, high-power microwave pulse that sweeps through a wide range of frequencies (a "chirp") to simultaneously excite multiple rotational transitions.[5] The subsequent free induction decay (FID), which contains the spectral information of all excited transitions, is then recorded and Fourier transformed to yield the frequency-domain spectrum.[3] The ability to collect a broad spectrum in a single experiment dramatically reduces data acquisition time compared to traditional cavity-based methods, making it ideal for the study of complex molecules and mixtures.[6][7]
Experimental Protocol: CP-FTMW Spectroscopy
-
Sample Preparation:
-
For volatile liquids, place a small amount in a sample holder upstream of the pulsed valve. The vapor will be entrained in a carrier gas.
-
For solids, gentle heating may be required to achieve sufficient vapor pressure. The heated sample reservoir should be placed just before the nozzle.
-
For non-volatile solids, laser ablation can be used to generate a plume of gas-phase molecules that are then cooled in the supersonic expansion.
-
The sample is seeded in an inert carrier gas, typically Neon or Argon, at a backing pressure of 1-3 atm.
-
-
Instrument Setup:
-
An arbitrary waveform generator (AWG) is used to create a chirped pulse, typically with a duration of 1-5 µs and covering a bandwidth of several GHz.[7]
-
The chirped pulse is amplified by a traveling-wave tube (TWT) amplifier to high power (typically 10-1000 W).[5]
-
The amplified pulse is broadcast into a vacuum chamber via a horn antenna.
-
The sample mixture is introduced into the chamber through a pulsed nozzle, creating a supersonic expansion that cools the molecules to rotational temperatures of a few Kelvin. This simplifies the spectrum by depopulating higher energy rotational states.
-
-
Data Acquisition:
-
Following the excitation pulse, the coherent emission from the polarized molecules (the FID) is detected by a second horn antenna.
-
The FID is amplified by a low-noise amplifier and digitized by a high-speed oscilloscope.[3]
-
Multiple FIDs are coherently averaged to improve the signal-to-noise ratio. The noise level decreases with the square root of the number of averages.[8]
-
-
Data Processing:
-
The averaged FID is Fourier transformed to obtain the frequency-domain rotational spectrum.
-
The resulting spectrum is then analyzed to identify and assign the rotational transitions.
-
Quantitative Performance of CP-FTMW Spectroscopy
| Parameter | Typical Value | Reference |
| Frequency Range | 2-18 GHz (and other bands) | [9] |
| Resolution | ~10 kHz | [3] |
| Measurement Time Reduction (vs. Cavity FTMW) | Factor of >1000 | [6] |
| Sample Consumption Reduction (vs. Cavity FTMW) | Factor of ~20 | [7] |
Double Resonance Spectroscopy
Double resonance spectroscopy is a powerful technique for simplifying and confirming assignments in complex rotational spectra.[10] This method involves the simultaneous application of two radiation fields: a "pump" field and a "probe" field. The pump field is used to selectively excite a specific rotational transition, which alters the population of the connected energy levels. The probe field is then used to monitor the effect of the pump on other transitions that share a common energy level.[11] This allows for the unambiguous linking of transitions that belong to the same molecule and even the same conformational isomer.
Experimental Protocol: Microwave-Microwave Double Resonance
-
Initial Broadband Scan:
-
Acquire a broadband survey spectrum using CP-FTMW spectroscopy to identify potential rotational transitions.
-
-
Pump Frequency Selection:
-
Select a strong, well-resolved transition from the survey spectrum to be the "pump" transition.
-
-
Probe Frequency Scan:
-
Set the frequency of the pump radiation source to be resonant with the selected transition.
-
Scan the frequency of the probe radiation source over the range of other potential transitions.
-
-
Signal Detection:
-
Monitor the intensity of the probe transitions as a function of the probe frequency.
-
A change in the intensity or line shape of a probe transition when the pump is on resonance confirms that the pump and probe transitions share a common energy level.
-
-
Automated Microwave Double Resonance (AMDOR):
-
This is an advanced implementation where the process is automated.[12] A broadband chirped-pulse spectrum is first acquired. Then, individual lines from this spectrum are systematically used as pump frequencies while a cavity FTMW spectrometer is used for sensitive detection of the connected probe transitions.[13] This creates a 2D "barcode" for each molecule, greatly facilitating the analysis of complex mixtures.[12]
-
Machine Learning and Pattern Recognition
The analysis of complex rotational spectra is increasingly benefiting from the application of machine learning and artificial intelligence.[14] These computational techniques can be trained to recognize the intricate patterns present in rotational spectra, enabling automated assignment and even the prediction of molecular properties directly from the spectral data.[15] For spectra that are too dense for manual analysis, machine learning offers a path forward for extracting valuable chemical information.[16]
Workflow for Machine Learning-Based Spectral Analysis
-
Data Generation/Collection:
-
A large training dataset of theoretical rotational spectra is generated. This can be done by calculating spectra for a wide variety of molecular structures and Hamiltonians.[14] Using calculated spectra for non-existent molecules can also be employed to create a diverse training set.[15]
-
Alternatively, experimental spectra can be used for training if a sufficiently large and well-annotated dataset is available.
-
-
Model Training:
-
A neural network model, such as a convolutional neural network (CNN) or a fully connected neural network (FCNN), is trained on the generated dataset.[17][18]
-
The model learns to correlate spectral features (e.g., transition frequencies and intensities) with the underlying molecular parameters (e.g., rotational constants, molecular structure).[15]
-
-
Spectral Analysis:
-
An experimental spectrum is pre-processed (e.g., noise reduction, baseline correction) and fed into the trained model.
-
The model then performs one or more of the following tasks:
-
Classification: Identifies the type of molecule (e.g., linear, symmetric top, asymmetric top).[15]
-
Parameter Regression: Predicts the rotational and centrifugal distortion constants.[17]
-
Structure Prediction: In more advanced applications, the model can predict molecular properties such as functional groups or even generate a SMILES string representation of the molecule.[19]
-
-
-
Validation:
-
The predictions from the machine learning model are validated by comparing them with the results of traditional fitting methods or by using the predicted parameters to simulate a spectrum and comparing it to the experimental data.
-
Quantitative Performance of Machine Learning in Rotational Spectroscopy
| Application | Performance Metric | Value/Observation | Reference |
| Chiral Analysis (M3WM) | Enantiomeric Excess (ee) Determination | 49.8 ± 5.1% (matches known sample) | [20] |
| Chiral Analysis (Chiral Tag) | Enantiomeric Excess (ee) Determination | 46.7 ± 0.2% (matches known sample) | [20] |
| Automated Assignment | Prediction Time | ~50 µs | [15] |
Visualizations
Experimental Workflow for CP-FTMW Spectroscopy
Caption: Workflow for CP-FTMW spectroscopy.
Logical Diagram of Double Resonance Spectroscopy
Caption: Principle of double resonance spectroscopy.
Workflow for Machine Learning-Assisted Spectral Analysis
Caption: Machine learning workflow for spectral analysis.
References
- 1. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 2. chem.libretexts.org [chem.libretexts.org]
- 3. Chirped-pulse Fourier Transform Microwave (CP-FTMW) Spectroscopy | Chemistry | Harvey Mudd College [hmc.edu]
- 4. chemtube3d.com [chemtube3d.com]
- 5. pubs.aip.org [pubs.aip.org]
- 6. Libra ETD [libraetd.lib.virginia.edu]
- 7. pubs.aip.org [pubs.aip.org]
- 8. researchgate.net [researchgate.net]
- 9. Chirped-Pulse Microwave Spectroscopy – Combustion Research Facility [crf.sandia.gov]
- 10. pubs.aip.org [pubs.aip.org]
- 11. repository.ubn.ru.nl [repository.ubn.ru.nl]
- 12. pubs.aip.org [pubs.aip.org]
- 13. [PDF] Automated microwave double resonance spectroscopy: A tool to identify and characterize chemical compounds. | Semantic Scholar [semanticscholar.org]
- 14. pubs.aip.org [pubs.aip.org]
- 15. osti.gov [osti.gov]
- 16. researchgate.net [researchgate.net]
- 17. pubs.aip.org [pubs.aip.org]
- 18. mdpi.com [mdpi.com]
- 19. ideals.illinois.edu [ideals.illinois.edu]
- 20. Assessing the performance of rotational spectroscopy in chiral analysis - PMC [pmc.ncbi.nlm.nih.gov]
Troubleshooting & Optimization
troubleshooting spectral line broadening in rotational spectroscopy
This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to address common issues related to spectral line broadening in rotational spectroscopy. The content is tailored for researchers, scientists, and drug development professionals.
Troubleshooting Guides
This section provides a question-and-answer format to directly address specific issues you might encounter during your experiments.
Issue: Observed spectral lines are broader than the natural linewidth.
1. Is the sample pressure too high?
High sample pressure leads to frequent molecular collisions, causing pressure broadening (also known as collisional broadening). This is often the dominant broadening mechanism at pressures above a few millitorr.
-
Troubleshooting Steps:
-
Monitor the pressure in the sample cell.
-
Systematically reduce the sample pressure and acquire spectra at different pressures.
-
Observe if the linewidth decreases with decreasing pressure.
-
-
Corrective Action: Reduce the sample pressure to the lowest possible value that still provides an adequate signal-to-noise ratio. For many rotational spectrometers, the optimal pressure range is typically between 1 and 100 mTorr.[1]
2. Is the sample temperature too high?
Higher temperatures increase the random thermal motion of molecules, leading to Doppler broadening . The magnitude of this broadening is proportional to the square root of the temperature.[2][3]
-
Troubleshooting Steps:
-
Measure the temperature of the sample cell.
-
If possible, cool the sample cell and observe the effect on the spectral linewidths.
-
-
Corrective Action:
-
Implement a cooling system for the sample cell. Techniques like supersonic jet expansion or cryogenic cooling can significantly reduce the sample temperature.
-
Employ sub-Doppler spectroscopic techniques such as Lamb-dip spectroscopy.[1]
-
3. Is the microwave/terahertz radiation power too high?
High radiation power can lead to saturation broadening . This occurs when the population of the upper and lower rotational states becomes nearly equal due to a high rate of induced transitions, leading to a broader spectral line.
-
Troubleshooting Steps:
-
Systematically reduce the power of the radiation source.
-
Acquire spectra at different power levels and observe any changes in linewidth.
-
-
Corrective Action: Reduce the radiation power to a level that avoids saturation while maintaining a good signal-to-noise ratio.
4. Are there issues with the spectrometer?
Instrumental effects can significantly contribute to the observed linewidth. This can be due to the spectrometer's resolution, electronic noise, or improper calibration.
-
Troubleshooting Steps:
-
Verify the resolution of your spectrometer.
-
Check for and minimize sources of electronic noise.
-
Perform a calibration of the spectrometer using a known standard with narrow spectral lines.
-
-
Corrective Action:
-
If the resolution is insufficient, consider using a higher-resolution instrument.
-
Improve grounding and shielding to reduce electronic noise.
-
Regularly calibrate the instrument according to the manufacturer's recommended procedures.
-
Logical Troubleshooting Workflow
The following diagram illustrates a logical workflow for troubleshooting spectral line broadening.
Caption: A flowchart for systematically troubleshooting spectral line broadening.
Quantitative Data Summary
The following table summarizes typical parameters and their effects on spectral line broadening in rotational spectroscopy.
| Broadening Mechanism | Typical Linewidth Contribution | Pressure Dependence | Temperature Dependence |
| Pressure Broadening | 1-10 MHz/Torr | Linear increase with pressure | Generally decreases with increasing temperature |
| Doppler Broadening | 10s of kHz to several MHz | Independent of pressure | Proportional to the square root of temperature |
| Saturation Broadening | Variable | Indirectly dependent on pressure through relaxation rates | Minor dependence |
| Instrumental Broadening | Dependent on spectrometer resolution | None | None |
Experimental Protocols
Protocol 1: Mitigation of Pressure Broadening
Objective: To reduce collisional broadening by optimizing the sample pressure.
Methodology:
-
Introduce the gaseous sample into the spectrometer's sample cell.
-
Start with a relatively high pressure (e.g., 200 mTorr) and record the rotational spectrum.
-
Measure the full width at half maximum (FWHM) of a well-resolved spectral line.
-
Gradually decrease the pressure in steps (e.g., 150 mTorr, 100 mTorr, 50 mTorr, 20 mTorr, 10 mTorr).
-
At each pressure step, record the spectrum and measure the FWHM of the same spectral line.
-
Plot the FWHM as a function of pressure.
-
Identify the pressure at which the linewidth is minimized without significant loss of signal intensity. This is the optimal operating pressure.
Protocol 2: Lamb-Dip Spectroscopy for Sub-Doppler Resolution
Objective: To overcome Doppler broadening and resolve closely spaced spectral features.
Methodology:
-
The experimental setup typically consists of a tunable radiation source, a sample cell, a detector, and optics to create two counter-propagating beams (a strong "pump" beam and a weak "probe" beam) from the same source.[4][5]
-
The pump beam and the probe beam are directed through the sample cell in opposite directions.
-
The frequency of the radiation source is scanned across the rotational transition of interest.
-
The pump beam saturates the transition for a specific velocity group of molecules.
-
When the laser frequency is tuned to the center of the Doppler-broadened line, both the pump and probe beams interact with the same group of molecules (those with a near-zero velocity component along the beam path).[5]
-
This interaction results in a sharp decrease in the absorption of the probe beam, creating a narrow "Lamb dip" at the center of the Doppler-broadened peak.[5][6]
-
The width of the Lamb dip is primarily limited by the natural linewidth and pressure broadening, not Doppler broadening.
Signaling Pathway and Relationship Diagram
The following diagram illustrates the relationships between different line broadening mechanisms.
Caption: The main contributors to observed spectral line broadening.
Frequently Asked Questions (FAQs)
Q1: What is the dominant source of line broadening in my rotational spectrum?
A1: The dominant source of broadening depends on your experimental conditions. At pressures above a few millitorr, pressure broadening is often the main contributor. At very low pressures and high temperatures, Doppler broadening may become more significant. If you are using high radiation power, saturation broadening could be a factor. Instrumental broadening is always present and depends on the quality of your spectrometer.
Q2: How can I distinguish between Doppler and pressure broadening?
A2: You can distinguish between these two effects by varying the sample pressure. Pressure broadening is directly proportional to pressure, so the linewidth will decrease as you lower the pressure. Doppler broadening is independent of pressure.
Q3: What is a Voigt profile?
A3: A Voigt profile is a convolution of a Gaussian and a Lorentzian profile. It is often used to model spectral lines when both Doppler (Gaussian) and pressure (Lorentzian) broadening are significant.
Q4: Can I completely eliminate line broadening?
A4: While you cannot completely eliminate all sources of broadening (the natural linewidth is a fundamental limit), you can significantly reduce the dominant contributions through careful control of experimental parameters like pressure, temperature, and radiation power, as well as by using advanced techniques like Lamb-dip spectroscopy.
Q5: How does collisional cooling help in reducing line broadening?
A5: Collisional cooling, often achieved by introducing a cold buffer gas (like helium or argon) into the sample chamber, reduces the translational temperature of the analyte molecules through collisions.[7][8] This reduction in temperature leads to a narrower velocity distribution and therefore a decrease in Doppler broadening. It can also influence the collisional environment, potentially affecting pressure broadening.
References
- 1. researchgate.net [researchgate.net]
- 2. physicsopenlab.org [physicsopenlab.org]
- 3. Atomic Spectroscopy - Spectral Line Shapes, etc. | NIST [nist.gov]
- 4. Lamb-Dip Laser-Induced Fluorescence Spectroscopy in a Supersonic Plasma Jet for Isotope Identification [jstage.jst.go.jp]
- 5. moodle2.units.it [moodle2.units.it]
- 6. scispace.com [scispace.com]
- 7. Rotational ‘cooling’ and ‘heating’ of OH+(3Σ−) by collisions with He: quantum dynamics revealing propensity rules under ion trap conditions - PMC [pmc.ncbi.nlm.nih.gov]
- 8. pubs.aip.org [pubs.aip.org]
Technical Support Center: Optimizing Microwave Spectra of Asymmetric Tops
Welcome to the technical support center for optimizing resolution in microwave spectra of asymmetric top molecules. This resource provides troubleshooting guides and frequently asked questions (FAQs) to assist researchers, scientists, and drug development professionals in overcoming common experimental challenges.
Frequently Asked Questions (FAQs)
Q1: What are the primary factors that limit the resolution of microwave spectra in asymmetric top molecules?
A1: The resolution of microwave spectra is primarily limited by several line broadening mechanisms.[1][2] Understanding these factors is the first step toward optimizing your experimental results. The main contributors are:
-
Doppler Broadening: This arises from the thermal motion of molecules in the gas sample. Molecules moving towards the microwave source absorb at slightly higher frequencies, while those moving away absorb at slightly lower frequencies, resulting in a broadened spectral line.[3][4][5] The resulting line profile is Gaussian.[2][6]
-
Pressure (Collisional) Broadening: Collisions between molecules in the gas phase can interrupt the interaction with the microwave radiation, leading to a broadening of the spectral lines.[6][7] This effect is more significant at higher pressures and results in a Lorentzian line shape.[2]
-
Power (Saturation) Broadening: When the microwave power is too high, it can lead to a saturation of the transition. This means the populations of the upper and lower energy levels become nearly equal, which can cause the spectral line to broaden.[8]
-
Modulation Broadening: In spectrometers that use techniques like Stark modulation, the modulation frequency and amplitude can contribute to the overall line width if not properly optimized.
Q2: My spectral lines are broad due to the Doppler effect. How can I minimize this?
A2: Reducing Doppler broadening is crucial for resolving fine and hyperfine structures in your spectra.[3] Since Doppler broadening is dependent on the temperature and velocity distribution of the molecules, the most effective methods involve cooling the sample.[4][5][6]
-
Supersonic Expansion: Expanding the gas sample through a small nozzle into a vacuum chamber causes significant cooling, which reduces the velocity distribution of the molecules and, consequently, the Doppler broadening.
-
Collisional Cooling: Introducing a cold buffer gas can cool the sample molecules through collisions.
-
Laser Cooling: While more complex to implement for molecules than for atoms, laser cooling can dramatically reduce the temperature of the sample.[9]
A common and effective method is to use a molecular beam, which collimates the gas flow and reduces the velocity component along the direction of the microwave propagation.[3]
Q3: How do I determine the optimal sample pressure for my experiment?
A3: The optimal sample pressure is a trade-off between signal intensity and resolution. Higher pressure increases the number of molecules interacting with the microwave radiation, leading to a stronger signal. However, it also increases the rate of molecular collisions, which causes significant pressure broadening.[7][10]
To find the optimal pressure, you should systematically vary the pressure while monitoring both the signal-to-noise ratio and the linewidth of a specific transition. Start at a low pressure and gradually increase it until you observe a noticeable broadening of the spectral lines. The optimal pressure will be the point just before pressure broadening becomes the dominant factor limiting your resolution.
Table 1: Effect of Sample Pressure on Microwave Spectra
| Pressure | Signal Intensity | Collisional Broadening | Overall Resolution |
| Low | Lower | Minimal | High |
| Medium | Optimal | Moderate | Optimal |
| High | High | Significant | Low |
Q4: What is power broadening and how can I avoid it?
A4: Power broadening, also known as saturation broadening, occurs when the intensity of the microwave radiation is too high.[8][11][12] This can cause the population of the upper and lower rotational energy levels to equalize, leading to a broadened spectral line and a reduction in the net absorption signal.
To avoid power broadening, it is essential to use the lowest microwave power that provides an adequate signal-to-noise ratio. You can test for power broadening by systematically reducing the microwave power and observing the linewidth. If the linewidth decreases as you lower the power, then power broadening was a contributing factor.
Table 2: Relationship Between Microwave Power and Spectral Linewidth
| Microwave Power | Signal Intensity | Power Broadening | Linewidth |
| High | May decrease due to saturation | Significant | Broad |
| Optimal | Good | Minimal | Narrow |
| Low | Low | Negligible | Narrow (limited by other factors) |
Troubleshooting Guide
Problem: My spectral lines are broad and unresolved.
This guide will walk you through a systematic process to identify and address the cause of poor resolution in your microwave spectra.
Caption: Troubleshooting workflow for broad spectral lines.
Experimental Protocols
Protocol 1: Minimizing Pressure Broadening
This protocol outlines the steps to find the optimal sample pressure for high-resolution microwave spectroscopy.
Objective: To reduce collisional broadening by finding the lowest possible sample pressure that maintains an adequate signal-to-noise ratio.
Materials:
-
Microwave spectrometer
-
Vacuum system with a precision pressure gauge
-
Gas sample of the asymmetric top molecule
Procedure:
-
Initial Pump Down: Evacuate the sample cell to the lowest possible pressure to remove any contaminants.
-
Introduce Sample at Low Pressure: Introduce the gas sample into the cell at a very low pressure (e.g., a few mTorr).
-
Acquire Initial Spectrum: Set the microwave power to a low, non-saturating level. Scan a known rotational transition and record the spectrum.
-
Measure Linewidth and Signal-to-Noise: Analyze the spectral line to determine its full width at half maximum (FWHM) and the signal-to-noise ratio (S/N).
-
Incremental Pressure Increase: Slowly increase the sample pressure by a small, controlled amount.
-
Repeat Spectral Acquisition: For each pressure increment, re-acquire the spectrum of the same rotational transition.
-
Data Analysis: Record the FWHM and S/N at each pressure point.
-
Determine Optimal Pressure: Plot the FWHM and S/N as a function of pressure. The optimal pressure is the point where the S/N is maximized before a significant increase in the FWHM is observed.
Caption: Workflow for optimizing sample pressure.
References
- 1. Broadening of Spectral Lines [hyperphysics.phy-astr.gsu.edu]
- 2. Atomic Spectroscopy - Spectral Line Shapes, etc. | NIST [nist.gov]
- 3. tf.nist.gov [tf.nist.gov]
- 4. laserscientist.com [laserscientist.com]
- 5. Doppler broadening - Wikipedia [en.wikipedia.org]
- 6. Spectral line - Wikipedia [en.wikipedia.org]
- 7. fiveable.me [fiveable.me]
- 8. researchgate.net [researchgate.net]
- 9. analyticalscience.wiley.com [analyticalscience.wiley.com]
- 10. home.strw.leidenuniv.nl [home.strw.leidenuniv.nl]
- 11. arxiv.org [arxiv.org]
- 12. Defying Conventional Wisdom in Spectroscopy: Power Narrowing on IBM Quantum [arxiv.org]
Technical Support Center: Centrifugal Distortion in Symmetric Top Molecules
This guide provides troubleshooting advice and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals encountering issues with centrifugal distortion in the rotational spectra of symmetric top molecules.
Frequently Asked Questions (FAQs)
Q1: What is centrifugal distortion and why does it occur in symmetric top molecules?
A: Molecules are not perfectly rigid structures.[1] When a molecule rotates, centrifugal force causes its bonds to stretch and bond angles to change slightly. This distortion alters the molecule's moments of inertia. Since the rotational energy levels are dependent on the moments of inertia, this distortion causes the energy levels to shift from the values predicted by the rigid rotor model.[1] This effect is known as centrifugal distortion, and it becomes more pronounced at higher rotational quantum numbers (J).[1]
Q2: My spectral fit using the rigid rotor model is poor, especially for high J transitions. How do I correct for this?
A: A poor fit at high J values is a classic indicator that centrifugal distortion is significant. The rigid rotor model assumes constant rotational constants (A, B, C), but in reality, these change with rotational speed. To correct for this, you must include centrifugal distortion constants in your Hamiltonian for the spectral analysis.
The energy levels (in wavenumber units, cm⁻¹) of a prolate symmetric top molecule, including first-order centrifugal distortion, are given by:
Fv(J, K) = BvJ(J+1) + (Av - Bv)K² - DJJ²(J+1)² - DJKJ(J+1)K² - DKK⁴[2]
Including the DJ, DJK, and DK terms in your fitting model will typically account for the deviations and improve the quality of your spectral fit.
Q3: What do the primary centrifugal distortion constants (DJ, DJK, DK) represent?
A: These constants account for the lowest-order effects of centrifugal distortion on the rotational energy levels.
-
DJ: This constant describes the stretching of the molecule due to the end-over-end rotation of the molecule. It is generally positive because the resulting increase in the moment of inertia lowers the energy of the rotational levels.[2]
-
DJK: This term represents the interaction between the rotation about the symmetry axis and the end-over-end rotation.[2] Its sign can be positive or negative. For example, for molecules like CFCl₃ and CHCl₃, where the center of mass is within the "umbrella" of the halogen atoms, DJK has been observed to be negative.[3]
-
DK: This constant accounts for the distortion caused by the rotation of the molecule purely about its symmetry axis.[2]
The following table summarizes these constants.
| Constant | Description | Typical Order of Magnitude (cm⁻¹) |
| DJ | Correction for end-over-end rotation. | 10⁻⁹ to 10⁻⁷ |
| DJK | Coupling between parallel and perpendicular rotation. | 10⁻⁹ to 10⁻⁷ |
| DK | Correction for rotation about the symmetry axis. | 10⁻⁹ to 10⁻⁷ |
Note: The pure rotational spectrum of a symmetric top molecule does not provide information about Av or DK because the selection rule is ΔK = 0.[1][2]
Q4: My fit is still not satisfactory after including quartic distortion constants. What is the next step?
A: If including the quartic constants (DJ, DJK, DK) is insufficient, especially for very high-resolution spectra or molecules with large-amplitude motions, you may need to include higher-order (sextic) centrifugal distortion constants. These are typically labeled HJ, HJK, HKJ, and HK.[2]
The energy expression becomes: Fv(J, K) = ... [quartic terms] + HJJ³(J+1)³ + HJKJ²(J+1)²K² + HKJJ(J+1)K⁴ + HKK⁶
These constants are significantly smaller than their quartic counterparts and should only be included in the fit if there is a statistically significant improvement and they can be determined with reasonable precision.
Q5: What is a "reduced Hamiltonian" and do I need to use one for a symmetric top molecule?
A: A reduced Hamiltonian is a transformed version of the full rotational Hamiltonian where some terms are mathematically combined to reduce the number of fittable parameters without losing accuracy in describing the energy levels.[4] This is crucial for asymmetric top molecules where the standard Hamiltonian contains more parameters than can be determined from the spectrum, leading to high correlations.[4][5] Watson's A- and S-reduced Hamiltonians are common examples.[5][6]
For symmetric top molecules, this issue is less common in standard analyses. However, in cases of accidental resonances or complex interactions in excited vibrational states, unitary transformations are used to create correlation-free reduced Hamiltonians suitable for fitting highly accurate spectroscopic data.[7] For most ground-state analyses, the standard energy expression is sufficient.
Troubleshooting Workflow
If you are having trouble fitting a rotational spectrum, follow this logical workflow to diagnose and correct for centrifugal distortion.
References
- 1. research.cbc.osu.edu [research.cbc.osu.edu]
- 2. web.gps.caltech.edu [web.gps.caltech.edu]
- 3. pubs.aip.org [pubs.aip.org]
- 4. pubs.aip.org [pubs.aip.org]
- 5. Asymmetric Top Hamiltonian [pgopher.chm.bris.ac.uk]
- 6. Asymmetric Top Hamiltonian [pgopher.chm.bris.ac.uk]
- 7. worldscientific.com [worldscientific.com]
Technical Support Center: Rotational Spectroscopy of Asymmetric Top Molecules
This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to assist researchers, scientists, and drug development professionals in assigning rotational transitions for asymmetric top molecules.
Frequently Asked Questions (FAQs)
Q1: Why is it so difficult to assign the rotational spectrum of my asymmetric top molecule?
Assigning the rotational spectrum of an asymmetric top molecule is inherently more complex than for linear or symmetric top molecules. The primary challenges include:
-
Irregular Energy Level Distribution: Unlike symmetric tops, there is no simple analytical formula to predict the rotational energy levels of an asymmetric top.[1][2][3] This results in an irregular and often dense spectral pattern.
-
Complex Selection Rules: The selection rules depend on the orientation of the molecule's permanent dipole moment relative to its principal axes of inertia.[4] This can lead to a large number of allowed transitions, further congesting the spectrum.[5][6]
-
Lack of Obvious Patterns: The combination of irregular energy levels and complex selection rules means that the resulting spectrum often lacks the clear, repeating patterns seen for simpler molecules, making initial assignments challenging.[7]
Q2: My predicted spectrum from quantum chemical calculations doesn't match the experimental one. What should I do?
This is a common issue. While quantum chemistry provides an excellent starting point, discrepancies are expected. Here’s a troubleshooting workflow:
-
Verify the Prediction Accuracy: The accuracy of the predicted rotational constants (A, B, C) is highly dependent on the level of theory and basis set used.[8] Ensure your chosen method is appropriate for your molecule.
-
Look for Characteristic Patterns: Even in a dense spectrum, certain patterns can emerge. For near-prolate or near-oblate tops, look for groupings of lines that resemble the simpler patterns of symmetric tops.[7]
-
Utilize Loomis-Wood Plots: Software that can generate Loomis-Wood plots can be invaluable for identifying series of related transitions (e.g., branches) that may not be obvious in a simple frequency plot.[1]
-
Check for Centrifugal Distortion Effects: For higher J quantum numbers, centrifugal distortion can significantly shift line positions from the rigid rotor prediction.[5] Ensure your prediction software accounts for these effects.
-
Consider Vibrational Satellites: If your experiment was not conducted at very low temperatures, you may be observing transitions from low-lying excited vibrational states. These "satellite" spectra will overlap with the ground state spectrum.
Q3: I have a very dense spectrum with many overlapping lines. How can I confirm my assignments?
Confirming assignments in a dense spectrum requires systematic approaches. Here are some recommended techniques:
-
Combination Differences: A powerful method for confirming assignments is to look for loops of transitions that share common energy levels. The sum of the frequencies of one path in the loop should equal the sum of the frequencies of the other path.
-
Double Resonance Spectroscopy: Techniques like microwave-microwave double resonance can definitively link transitions that share a common energy level.[9] This is a highly effective method for filtering out unrelated transitions and confirming assignments.[1]
-
Isotopic Substitution: If you can synthesize and measure the spectra of isotopologues of your molecule, the predictable shifts in the rotational constants can help confirm the assignment of specific transitions.[1]
Troubleshooting Guides
Problem: I can't find any recognizable patterns in my spectrum.
Solution Workflow:
Caption: Troubleshooting workflow for unassigned spectra.
Problem: My spectral fit is not converging or has large errors.
Solution Workflow:
Caption: Workflow for improving a poor spectral fit.
Quantitative Data Summary
The following table summarizes typical rotational and centrifugal distortion constants for a few representative asymmetric top molecules. These values can serve as a rough guide for the order of magnitude to expect for similar molecules.
| Molecule | A (MHz) | B (MHz) | C (MHz) | D_J (kHz) | D_JK (kHz) |
| Formaldehyde (H₂CO) | 281970.5 | 38835.8 | 34004.2 | 81.7 | 1550 |
| Water (H₂O) | 835839.6 | 435351.0 | 278140.4 | 3340 | -14900 |
| Pyridine (C₅H₅N) | 5992.3 | 5809.1 | 2933.2 | 0.9 | -1.9 |
Experimental Protocols
Key Experiment: Broadband Rotational Spectroscopy
This technique is often the first step in analyzing a new molecule.
Methodology:
-
Sample Preparation: The molecule of interest is seeded in a carrier gas (e.g., Neon, Argon) at low concentrations (typically <1%).
-
Supersonic Expansion: The gas mixture is expanded through a pulsed nozzle into a high-vacuum chamber. This cools the molecules to a very low rotational temperature (typically 1-5 K), which simplifies the spectrum by depopulating higher energy rotational states.
-
Microwave Excitation: A short, high-power pulse of broadband microwave radiation is used to excite a wide range of rotational transitions simultaneously.
-
Free Induction Decay (FID) Detection: After the excitation pulse, the coherently rotating molecules emit a faint microwave signal, known as the Free Induction Decay (FID). This signal is detected by a sensitive antenna.
-
Fourier Transformation: The time-domain FID signal is digitized and then Fourier transformed to produce the frequency-domain rotational spectrum.
-
Data Analysis: The resulting spectrum is analyzed using specialized software to identify and assign transitions.
Key Experiment: Microwave-Microwave Double Resonance
This technique is used to confirm assignments and link transitions that share a common energy level.
Methodology:
-
Initial Setup: The experiment is set up similarly to a standard rotational spectroscopy experiment.
-
Pump Transition: A strong, continuous-wave microwave source (the "pump") is tuned to a known or suspected rotational transition. This significantly alters the population of the two energy levels involved in this transition.
-
Probe Sweep: A second, weaker microwave source (the "probe") is swept over a range of frequencies.
-
Signal Detection: When the probe frequency matches a transition that shares an energy level with the pumped transition, a change in the absorption or emission signal is observed.
-
Confirmation: The observation of a double-resonance signal provides unambiguous confirmation that the pump and probe transitions are connected.
References
- 1. kups.ub.uni-koeln.de [kups.ub.uni-koeln.de]
- 2. web.gps.caltech.edu [web.gps.caltech.edu]
- 3. apps.dtic.mil [apps.dtic.mil]
- 4. ocw.mit.edu [ocw.mit.edu]
- 5. info.ifpan.edu.pl [info.ifpan.edu.pl]
- 6. weichman.princeton.edu [weichman.princeton.edu]
- 7. scribd.com [scribd.com]
- 8. jupiter.chem.uoa.gr [jupiter.chem.uoa.gr]
- 9. researchgate.net [researchgate.net]
Technical Support Center: Enhancing Signal-to-Noise Ratio in Rotational Spectroscopy
Welcome to the technical support center for rotational spectroscopy. This resource is designed for researchers, scientists, and drug development professionals to provide troubleshooting guidance and answers to frequently asked questions (FAQs) related to improving the signal-to-noise ratio (S/N) in your experiments.
Troubleshooting Guides
This section provides solutions to specific issues you might encounter during your rotational spectroscopy experiments that can lead to a poor signal-to-noise ratio.
Issue: My signal is very weak or completely absent.
This is a common and frustrating problem that can arise from multiple sources. Follow this guide to systematically identify and resolve the issue.
| Possible Cause | Solution | Experimental Protocol |
| No or Low Analyte Concentration in the Gas Phase | Ensure your sample is volatile enough and is being effectively introduced into the spectrometer. For non-volatile samples, consider heating the sample reservoir or using laser ablation. | Protocol for Sample Introduction: 1. For volatile liquids, ensure the carrier gas (e.g., Argon, Neon) is bubbling through the sample. 2. For solids, gently heat the sample holder to increase vapor pressure. Monitor the pressure in the chamber to avoid overwhelming the vacuum pumps. 3. For thermally labile or non-volatile solids, utilize a laser ablation source to generate a plume of the sample in the gas phase immediately before the supersonic expansion. |
| Inefficient Rotational Cooling | In supersonic jet expansions, inefficient cooling leads to the population of many rotational states, reducing the population in any single state and thus decreasing signal intensity.[1] | Protocol for Optimizing Supersonic Expansion: 1. Check the backing pressure of your pulsed nozzle. Typical pressures range from 1-10 bar. Higher backing pressures generally lead to better cooling. 2. Ensure the nozzle is functioning correctly and not clogged. 3. Optimize the timing of the gas pulse relative to the microwave excitation pulse. The molecular packet should be in the center of the microwave cavity during excitation. |
| Microwave Power is Too Low or Too High | Insufficient microwave power will not effectively polarize the molecules. Conversely, excessive power can lead to power broadening of the spectral lines, which can decrease the peak height and make them harder to distinguish from noise. | Protocol for Microwave Power Optimization: 1. Start with a low microwave power setting and gradually increase it while monitoring the signal intensity. 2. Observe the line width of your rotational transitions. If the line width starts to increase significantly with increasing power, you are likely in the power broadening regime. 3. Reduce the power to a level just below the onset of power broadening to achieve the best compromise between signal intensity and resolution. |
| Incorrect Frequency Range | You may be scanning a frequency range where your molecule does not have any rotational transitions. | Protocol for Frequency Prediction: 1. Use quantum chemical calculations (e.g., DFT or ab initio methods) to predict the rotational constants of your molecule.[2] 2. Use the predicted rotational constants to estimate the frequencies of the lowest J rotational transitions. 3. Center your initial scans around these predicted frequencies. |
| Detector Malfunction | The detector may not be functioning correctly, leading to a complete loss of signal. | Protocol for Detector Check: 1. Consult your spectrometer's manual for detector-specific diagnostic procedures. 2. Check the detector's power supply and connections. 3. If possible, test the detector with a known, strong signal from a reference sample. |
Troubleshooting Workflow for Weak or Absent Signal
Caption: Troubleshooting logic for a weak or absent signal.
Issue: My baseline is noisy, obscuring weak signals.
A high noise floor can make it difficult to distinguish real signals from background fluctuations.
| Possible Cause | Solution | Experimental Protocol |
| Phase Noise from Microwave Source | The stability of the microwave source is critical. Phase noise can be a significant contributor to the overall noise level.[3][4][5] | Protocol for Minimizing Phase Noise: 1. Ensure the microwave source has had adequate time to warm up and stabilize. 2. Use a high-quality, low-phase-noise microwave synthesizer. 3. If available, use a phase-locked loop (PLL) to stabilize the frequency of the source against a stable reference oscillator.[5] |
| Electrical Interference | External electrical noise from other equipment can be picked up by the detector and electronics. | Protocol for Reducing Electrical Interference: 1. Ensure all electronic components are properly grounded. 2. Use shielded cables for all signal-carrying lines. 3. If possible, physically move the spectrometer away from sources of high electrical noise (e.g., motors, high-power equipment). |
| Detector Noise | The detector itself is a source of noise. Operating the detector under optimal conditions can minimize its noise contribution. | Protocol for Optimizing Detector Performance: 1. For cryogenic detectors, ensure they are cooled to their optimal operating temperature. 2. Check the detector's bias voltage and adjust it according to the manufacturer's specifications for the best S/N. |
| Insufficient Signal Averaging | Signal averaging is a powerful technique to reduce random noise. The signal-to-noise ratio improves with the square root of the number of scans.[6] | Protocol for Signal Averaging: 1. Increase the number of free induction decays (FIDs) averaged. 2. Be aware that this will increase the experiment time. Determine a practical number of averages that provides a sufficient S/N for your analysis. |
| Vibrations | Mechanical vibrations can affect the alignment of the microwave optics and introduce noise. | Protocol for Vibration Isolation: 1. Place the spectrometer on a vibration isolation table. 2. Identify and mitigate sources of vibration in the laboratory. |
Noise Reduction Workflow
Caption: Workflow for reducing baseline noise.
Frequently Asked Questions (FAQs)
Q1: How does signal averaging improve the signal-to-noise ratio?
Signal averaging improves the S/N by reducing the contribution of random noise. The signal from the analyte is coherent and adds linearly with the number of scans (N), while random noise is incoherent and adds as the square root of the number of scans (√N). Therefore, the S/N improves by a factor of √N.[6]
| Number of Averages (N) | S/N Improvement Factor (√N) |
| 1 | 1 |
| 4 | 2 |
| 16 | 4 |
| 100 | 10 |
| 10,000 | 100 |
Q2: What is the purpose of a supersonic expansion in rotational spectroscopy?
A supersonic expansion is used to cool the gas-phase molecules to very low rotational temperatures (typically 1-10 K).[1] This cooling simplifies the rotational spectrum by collapsing the population of molecules into the lowest rotational energy levels. With a higher population in the lower J states, the transitions originating from these states will be more intense, leading to a significant improvement in the S/N for those transitions.[1]
Q3: What is Fourier filtering and how can it improve my spectra?
Fourier filtering is a computational technique that can be used to remove noise from your spectrum.[6] The process involves:
-
Performing a Fourier transform on your frequency-domain spectrum to convert it to the time domain.
-
In the time domain, the molecular signal (free induction decay or FID) typically decays over a relatively long time, while high-frequency noise appears as rapid oscillations.
-
A digital filter is applied to remove the high-frequency components (noise).
-
An inverse Fourier transform is then performed to convert the filtered time-domain signal back to the frequency domain, resulting in a spectrum with a higher S/N.
Q4: Can my choice of carrier gas affect the signal-to-noise ratio?
Yes, the choice of carrier gas can influence the S/N. Heavier carrier gases, such as Argon or Neon, are generally more effective at cooling molecules during the supersonic expansion than lighter gases like Helium. Better cooling leads to a more simplified spectrum and stronger signals for the lowest rotational transitions, as explained in Q2.
Q5: What is Stark modulation and how does it improve signal detection?
Stark modulation is a technique primarily used in waveguide-based microwave spectrometers. It involves applying a square-wave electric field (Stark field) to the sample. This field causes a shift in the energy levels of polar molecules (the Stark effect). By using a phase-sensitive detector locked to the modulation frequency, the spectrometer can selectively detect the signals that are modulated by the electric field. This technique is very effective at discriminating the molecular signal from background noise and instrumental drift, thereby significantly improving the S/N.[7][8]
Experimental Workflow for a Typical Chirped-Pulse FTMW Experiment
Caption: A typical experimental workflow for CP-FTMW spectroscopy.
References
- 1. Assessing the performance of rotational spectroscopy in chiral analysis - Chemical Science (RSC Publishing) DOI:10.1039/D0SC03752D [pubs.rsc.org]
- 2. mdpi.com [mdpi.com]
- 3. pubs.aip.org [pubs.aip.org]
- 4. mwrf.com [mwrf.com]
- 5. microwavejournal.com [microwavejournal.com]
- 6. chem.libretexts.org [chem.libretexts.org]
- 7. pubs.aip.org [pubs.aip.org]
- 8. Stark-modulated spectrometer | instrument | Britannica [britannica.com]
Technical Support Center: Determination of Rotational Constants
This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to assist researchers, scientists, and drug development professionals in accurately determining rotational constants from molecular spectroscopy experiments.
Frequently Asked Questions (FAQs)
Q1: What are the most common sources of error in determining rotational constants?
Errors in determining rotational constants can be broadly categorized into three types: systematic errors, random errors, and blunders.[1]
-
Systematic errors are consistent and reproducible, often arising from issues with instrumentation or experimental design.[1][2] Examples include improper instrument calibration, zero errors in measurement devices, and consistent misinterpretation of spectra.[3][4]
-
Random errors are unpredictable fluctuations in measurements, often due to environmental factors or inherent limitations of the equipment.[1][2] Examples include temperature and pressure fluctuations, electronic noise, and variations in detector sensitivity.[1][5]
-
Blunders are human errors, such as incorrect data recording, calculation mistakes, or improper sample preparation.[1]
A summary of common experimental errors is provided in the table below.
Q2: My spectral lines are broader than expected. What could be the cause?
Increased spectral line width can be a significant source of error and can arise from several factors:
-
Pressure Broadening: At higher sample pressures, intermolecular collisions become more frequent, which can shorten the lifetime of rotational states and lead to broader spectral lines.[6][7][8] This effect is proportional to the pressure.[6] To mitigate this, it is advisable to work with low sample pressures to minimize these collisions.
-
Doppler Broadening: This occurs due to the thermal motion of molecules in the gas phase. Molecules moving towards the detector will absorb at a slightly higher frequency, while those moving away will absorb at a slightly lower frequency, resulting in a broadened line.
-
Instrumental Resolution: The resolution of your spectrometer can also limit the observed line width. If the instrumental resolution is lower than the natural line width of the transition, the observed line will be broadened.[9] High-resolution microwave spectroscopy is often necessary to resolve fine details.[9]
-
Power Saturation: Using excessive microwave power can lead to saturation of the transition, which also results in line broadening. It is important to use the minimum power necessary to achieve a good signal-to-noise ratio.
Q3: I am having trouble assigning the rotational transitions in my spectrum. What are some common pitfalls?
Assigning rotational transitions, especially in complex spectra, can be challenging. Common difficulties include:
-
Overlapping Spectra: The presence of multiple conformers, isotopologues, or vibrationally excited states in the sample can lead to overlapping spectra, making it difficult to assign transitions to a specific species.[10][11]
-
Incorrect Initial Guess: The process of assigning spectra often relies on an initial prediction of the rotational constants from quantum chemical calculations.[10] If this initial guess is inaccurate, it can be very difficult to match the predicted spectrum to the experimental one.
-
Ignoring Centrifugal Distortion: The rigid rotor model is an approximation.[3] At higher rotational quantum numbers (J), centrifugal forces can stretch the bonds in a molecule, changing the moment of inertia and causing deviations from the simple rigid rotor energy level expression.[3] It is crucial to include centrifugal distortion constants in the analysis for accurate results.
-
Nuclear Quadrupole Coupling: If your molecule contains nuclei with a nuclear spin greater than 1/2 (e.g., ¹⁴N, ³⁵Cl, ¹²⁷I), the interaction of the nuclear quadrupole moment with the electric field gradient in the molecule can cause splitting of the rotational lines.[3][11] This hyperfine structure must be accounted for in the spectral analysis.[3]
Q4: My signal-to-noise ratio is poor. How can I improve it?
A low signal-to-noise ratio (S/N) can make it difficult to detect weak transitions and accurately determine line positions.[5][12] Here are some troubleshooting steps:
-
Check Sample Pressure: Ensure the sample pressure is optimal. While high pressure can lead to broadening, a pressure that is too low will result in a weak signal.
-
Instrument Tuning and Maintenance: Verify that the spectrometer is properly tuned and that all components are functioning correctly. Regular maintenance is crucial for optimal performance.
-
Signal Averaging: Increasing the number of scans and averaging the data is a common technique to improve the S/N ratio.[13]
-
Reduce Electronic Noise: Ensure that all electronic components are properly grounded and shielded to minimize interference from external sources.[5]
-
Optimize Detector Performance: Check the detector's specifications and ensure it is operating under optimal conditions (e.g., temperature for certain detectors).
Troubleshooting Guides
Guide 1: Systematic Errors in Rotational Constant Determination
| Symptom | Possible Cause | Troubleshooting Steps |
| All measured line frequencies are consistently shifted from theoretical predictions. | Instrument Calibration Error: The frequency source of the spectrometer is not accurately calibrated. | 1. Calibrate the spectrometer using a known standard with well-characterized rotational transitions (e.g., OCS, N₂O).[14]2. Regularly check and adjust the calibration as part of routine instrument maintenance. |
| The spacing between rotational lines is consistently larger or smaller than expected. | Zero Error in Measurement: An offset in the frequency measurement system. | 1. Check for any zero offset in the instrument's baseline.[4]2. Apply a zero correction to all measured frequencies if an offset is identified.[4] |
| Inaccurate bond lengths and angles derived from the rotational constants. | Inadequate Theoretical Model: The rigid rotor approximation is insufficient, and other effects are not being considered. | 1. Include centrifugal distortion terms in the Hamiltonian for the data analysis, especially for transitions involving high J values.[3]2. Account for vibration-rotation interactions by analyzing spectra in different vibrational states if possible.[3] |
Guide 2: Data Analysis and Interpretation Errors
| Symptom | Possible Cause | Troubleshooting Steps |
| Difficulty in finding a consistent fit for the observed spectral lines. | Misassignment of Transitions: Incorrectly assigning the quantum numbers (J) to the observed spectral lines. | 1. Use computational chemistry software to predict the rotational spectrum and use it as a guide for initial assignments.[10]2. Look for characteristic patterns, such as the nearly equal spacing of lines in the spectrum of a linear molecule.[15]3. Utilize software tools designed for automated spectral assignment and fitting.[16][17] |
| The fit is poor for high J transitions. | Neglecting Centrifugal Distortion: The effect of molecular stretching at higher rotational speeds is not accounted for. | 1. Add centrifugal distortion constants (e.g., D, H) to your fitting model.[3]2. Perform a new fit of the experimental data including these higher-order terms. |
| Observed lines are split into multiple components. | Unresolved Hyperfine Structure: The interaction of nuclear spins with the molecular rotation is not being considered. | 1. Identify any quadrupolar nuclei in your molecule.2. Use a fitting program that can account for nuclear quadrupole coupling to analyze the split lines.[3][11] |
Experimental Protocols
Key Experiment: Microwave Spectroscopy for Rotational Constant Determination
This protocol outlines the general steps for determining rotational constants using a microwave spectrometer.
1. Sample Preparation:
-
The sample must be in the gas phase.[18][19] For liquids or solids, this typically involves gentle heating to increase their vapor pressure.
-
The sample is introduced into a vacuum chamber, and the pressure is carefully controlled. A low pressure is generally used to minimize pressure broadening of the spectral lines.
2. Instrument Setup and Calibration:
-
The microwave spectrometer consists of a microwave source, an absorption cell, and a detector.[20]
-
The frequency of the microwave source is swept over the desired range.
-
Before running the sample, the instrument should be calibrated using a standard gas with well-known rotational transitions, such as carbonyl sulfide (B99878) (OCS) or nitrous oxide (N₂O).[14]
3. Data Acquisition:
-
A background spectrum is typically recorded with an empty absorption cell and subtracted from the sample spectrum to remove any instrumental artifacts.
-
The microwave radiation is passed through the sample cell, and the detector measures the intensity of the transmitted radiation as a function of frequency.
-
Absorption of microwaves by the sample at specific frequencies corresponds to transitions between rotational energy levels.
4. Data Analysis:
-
The resulting spectrum, a plot of absorption intensity versus frequency, will show a series of peaks corresponding to the rotational transitions.
-
The frequencies of these peaks are measured accurately.
-
The observed transition frequencies are then fitted to a theoretical model, such as the rigid rotor model, often including terms for centrifugal distortion.[3]
-
This fitting process yields the rotational constants (A, B, C) and any centrifugal distortion constants.[3]
Visualizations
Caption: Experimental workflow for determining rotational constants, highlighting potential error points.
Caption: Logical relationships between experimental errors and their impact on rotational constants.
References
- 1. Rotational–vibrational spectroscopy - Wikipedia [en.wikipedia.org]
- 2. royalsocietypublishing.org [royalsocietypublishing.org]
- 3. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 4. ncert.nic.in [ncert.nic.in]
- 5. azooptics.com [azooptics.com]
- 6. researchgate.net [researchgate.net]
- 7. academic.oup.com [academic.oup.com]
- 8. phys.libretexts.org [phys.libretexts.org]
- 9. Microwave spectroscopy - Wikipedia [en.wikipedia.org]
- 10. ideals.illinois.edu [ideals.illinois.edu]
- 11. info.ifpan.edu.pl [info.ifpan.edu.pl]
- 12. University of Ottawa NMR Facility Blog: Poor Signal-to-Noise Ratio in Your Spectrum? [u-of-o-nmr-facility.blogspot.com]
- 13. Extraction of Weak Spectroscopic Signals with High Fidelity: Examples from ESR - PMC [pmc.ncbi.nlm.nih.gov]
- 14. pubs.aip.org [pubs.aip.org]
- 15. m.youtube.com [m.youtube.com]
- 16. meetings.iac.es [meetings.iac.es]
- 17. mailman.cs.uchicago.edu [mailman.cs.uchicago.edu]
- 18. chem.libretexts.org [chem.libretexts.org]
- 19. chem.libretexts.org [chem.libretexts.org]
- 20. uomustansiriyah.edu.iq [uomustansiriyah.edu.iq]
how to handle overlapping spectral lines in complex molecules
Technical Support Center: Spectroscopy
Welcome to the technical support center for advanced spectroscopic analysis. This guide provides troubleshooting advice, frequently asked questions (FAQs), and protocols to help researchers, scientists, and drug development professionals handle overlapping spectral lines in complex molecules.
Frequently Asked Questions (FAQs)
Q1: What are the primary causes of spectral line overlap?
Spectral line overlap occurs when two or more distinct chemical species or different transitions within the same molecule produce signals at very similar frequencies or wavelengths. The primary causes include:
-
High Molecular Complexity: Large molecules, such as proteins or polymers, have numerous vibrational or electronic states, leading to a high density of spectral lines.
-
Sample Composition: Complex mixtures containing multiple structurally similar compounds will naturally produce overlapping spectra.[1]
-
Line Broadening Effects: Physical phenomena like Doppler broadening, pressure broadening, and short excited-state lifetimes cause spectral lines to broaden, increasing the likelihood of overlap.
-
Instrumental Limitations: The finite resolution of the spectrometer can limit its ability to distinguish between closely spaced spectral lines.[2]
Q2: What are the main strategies for resolving overlapping spectra?
There are two primary approaches to address spectral overlap: experimental methods that aim to improve the resolution of the raw data, and computational methods that mathematically separate the overlapping signals post-acquisition.[3]
-
Experimental Strategies: These include optimizing instrumental parameters (e.g., using a narrower spectrometer slit[2]), and employing advanced techniques like two-dimensional (2D) correlation spectroscopy.[4]
-
Computational Strategies: These involve mathematical algorithms to deconvolve the composite spectrum. Common methods include derivative spectroscopy, Fourier self-deconvolution, and multivariate curve resolution (MCR).[2][5]
Q3: When should I choose an experimental solution versus a computational one?
The choice depends on the experimental constraints and the nature of the sample.
-
Choose experimental methods when you have control over the sample preparation and data acquisition process. Techniques like 2D spectroscopy can provide deeper insights into molecular interactions and dynamics that computational methods cannot.[6][7]
-
Choose computational methods when you are working with existing data, when experimental options are limited, or for high-throughput analysis. These methods can be powerful for quantifying components in a mixture without the need for complete physical separation.[8][9]
Troubleshooting Guide
Q1: My deconvolution algorithm is producing non-physical results, like negative peaks. What can I do?
This is a common issue when the algorithm converges on a mathematically possible but chemically meaningless solution.[9]
-
Apply Constraints: Use a deconvolution method like Multivariate Curve Resolution with Alternating Least Squares (MCR-ALS) that allows for constraints. Applying a non-negativity constraint will force the algorithm to only consider solutions where both concentrations and spectral profiles are positive.[9]
-
Check Your Model: Ensure the chosen lineshape (e.g., Gaussian, Lorentzian, Voigt) is appropriate for your data. An incorrect peak shape model can lead to significant errors in the fitting routine.[10]
-
Improve Data Quality: High noise levels can mislead the algorithm. Improve the signal-to-noise ratio (S/N) of your spectrum by increasing the acquisition time or using a higher concentration of the sample, if possible.[10]
Q2: The deconvolution results are not consistent between runs. Why is this happening and how can I fix it?
Inconsistency often points to ambiguities in the deconvolution model, where multiple solutions fit the data almost equally well.
-
Provide a Better Initial Estimate: Some algorithms, like MCR, use an initial estimate to begin the iterative process. A poor initial estimate can lead to convergence on a local minimum rather than the true solution.[11] Providing an estimate based on the spectrum of a pure component can significantly improve reproducibility.
-
Reduce Model Complexity: The algorithm may be trying to fit too many peaks. Use prior knowledge of your sample to fix the number of components to a chemically reasonable value.[12]
-
Validate the Results: Always compare the mathematically resolved spectra with the known spectra of the pure components whenever possible to validate the accuracy of the deconvolution.[10]
Q3: I can't achieve baseline separation experimentally. What are my first steps for data processing?
When baseline separation is not possible, pre-processing the data is crucial before applying advanced deconvolution.
-
Baseline Correction: Use a suitable baseline correction algorithm to remove background signals and baseline drift. This is a critical first step for accurate quantification.
-
Derivative Spectroscopy: Calculating the first or second derivative of a spectrum can help separate overlapping peaks.[3][13] The first derivative can be used to find the exact position of peak maxima (zero-crossing points), while the second derivative enhances resolution by narrowing the peaks.[13]
-
Smoothing: Derivative methods are very sensitive to noise.[5] Apply a smoothing algorithm, such as the Savitzky-Golay filter, before taking the derivative to prevent noise amplification.[13][14]
Key Techniques & Experimental Protocols
Technique 1: Computational Deconvolution with MCR-ALS
Multivariate Curve Resolution-Alternating Least Squares (MCR-ALS) is a powerful chemometric technique that resolves mixed spectral signals into the pure spectra of the individual components and their corresponding concentration profiles.[8][15]
Caption: Workflow for MCR-ALS deconvolution.
-
Data Acquisition: Collect spectral data for your complex mixture over a period of time, or under varying conditions (e.g., pH, temperature). Arrange the data into a matrix D , where each row represents a spectrum at a different time point and each column represents an absorbance at a specific wavelength.
-
Data Pre-processing: Apply necessary pre-processing steps such as baseline correction to all spectra in D .
-
Estimate Number of Components: Use a method like Singular Value Decomposition (SVD) on matrix D to determine the number of independent chemical species in the mixture.
-
Initial Guess: Provide an initial estimate for either the pure spectra (S ) or the concentration profiles (C ). An initial guess for S can be the spectrum of one of the known pure components.
-
ALS Iteration:
-
Begin the iterative process. The MCR-ALS algorithm will alternate between calculating the best C for a given S , and the best S for a given C .
-
Apply chemical constraints at each iteration. The most common constraint is non-negativity for both spectra and concentrations.
-
-
Check for Convergence: The iteration continues until the change in the results between iterations is negligible, indicating that the algorithm has converged to a stable solution.
-
Analyze Results: The output will be the resolved pure component spectra matrix S and the concentration profile matrix C .[8]
Technique 2: Two-Dimensional Correlation Spectroscopy (2D-COS)
2D-COS is an analytical technique that is particularly useful for enhancing spectral resolution by spreading overlapping peaks across a second dimension.[4] It involves monitoring a sample's spectral response to an external perturbation (like temperature, pressure, or time) and then applying a correlation analysis to the data.[7]
Caption: Conceptual workflow of 2D Correlation Spectroscopy.
-
Sample Preparation: Prepare the sample as you would for a standard FT-IR measurement.
-
Apply Perturbation: Place the sample in a temperature-controlled cell. Define a temperature range and a ramp rate (e.g., from 30°C to 100°C at 5°C/minute).
-
Spectral Acquisition: Configure the FT-IR spectrometer to acquire spectra continuously as the temperature changes. This will generate a series of 1D spectra, each corresponding to a specific temperature.
-
Data Analysis:
-
Import the spectral series into a 2D-COS analysis software.
-
The software performs a mathematical correlation analysis on the dataset.
-
This generates two types of 2D correlation maps: a synchronous spectrum and an asynchronous spectrum .[16]
-
-
Interpretation:
-
Synchronous Spectrum: Peaks on the diagonal (autopeaks) correspond to the original 1D spectrum. Cross-peaks indicate that the intensity of two different spectral bands are changing together (in-phase) in response to the temperature change.[4][6]
-
Asynchronous Spectrum: Cross-peaks in this map only appear if the intensities of two spectral bands are changing out-of-phase. This is extremely effective for separating broadly overlapped peaks that may appear as a single band in the 1D spectrum.[4][16]
-
Data & Performance Comparison
Choosing the right computational method is critical. The table below provides a summary of common deconvolution techniques and their typical performance characteristics.
| Method | Principle | Pros | Cons | Best For |
| Derivative Spectroscopy | Calculates the 1st or 2nd derivative of the spectrum to narrow peaks and identify maxima.[3] | Simple to implement; fast computation. | Very sensitive to noise; can distort peak shapes and intensities.[5] | Quick qualitative analysis and peak position identification. |
| Fourier Self-Deconvolution (FSD) | Divides the Fourier transform of the spectrum by a lineshape function to narrow the peaks in the original spectrum.[2] | Can significantly enhance resolution. | Prone to creating artificial side-lobes (artifacts); requires careful parameter selection.[2] | High-resolution analysis where the underlying peak shape is well-known. |
| Curve Fitting (Peak Fitting) | Fits a set of known mathematical peak shapes (e.g., Gaussian, Lorentzian) to the experimental data. | Provides quantitative information (peak area, height, width). | Requires prior knowledge of the number of peaks and their shapes; can be computationally intensive.[2] | Systems with a known number of components and well-defined peak shapes. |
| Multivariate Curve Resolution (MCR) | Decomposes a spectral data matrix into pure component spectra and concentration profiles without prior spectral information.[9] | Does not require reference spectra; can handle complex systems and unknown components.[8] | Solutions can be ambiguous; may require constraints (e.g., non-negativity) to achieve a chemically meaningful result.[15] | Analyzing reaction kinetics, chromatographic data, and complex mixtures with unknown components.[17] |
References
- 1. spectroscopyonline.com [spectroscopyonline.com]
- 2. Critical Evaluation of Spectral Resolution Enhancement Methods for Raman Hyperspectra - PMC [pmc.ncbi.nlm.nih.gov]
- 3. Spectrophotometric approach for deconvolving overlapped spectra of antihypertensive drug mixtures using UV detection: an eco-friendly method - PMC [pmc.ncbi.nlm.nih.gov]
- 4. spectroscopyonline.com [spectroscopyonline.com]
- 5. scispace.com [scispace.com]
- 6. chem.libretexts.org [chem.libretexts.org]
- 7. researchgate.net [researchgate.net]
- 8. files01.core.ac.uk [files01.core.ac.uk]
- 9. Multivariate curve resolution (MCR) — chemometrics 0.4.0 documentation [chemometrics.readthedocs.io]
- 10. researchgate.net [researchgate.net]
- 11. Multivariate curve resolution combined with estimation by cosine similarity mapping of analytical data - Analyst (RSC Publishing) [pubs.rsc.org]
- 12. researchgate.net [researchgate.net]
- 13. nofima.com [nofima.com]
- 14. researchgate.net [researchgate.net]
- 15. researchgate.net [researchgate.net]
- 16. researchgate.net [researchgate.net]
- 17. Application of Multivariate curve resolution‐alternating least square methods on the resolution of overlapping CE peaks from different separation conditions | Semantic Scholar [semanticscholar.org]
calibration techniques for high-precision microwave spectrometers
This technical support center provides troubleshooting guides and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals using high-precision microwave spectrometers. The information is presented in a question-and-answer format to directly address specific issues encountered during experiments.
Troubleshooting Guides
This section provides solutions to common problems encountered during the operation and calibration of high-precision microwave spectrometers.
Issue: Distorted or Asymmetric Peak Shapes
Q1: My spectral lines are showing a tailing or fronting asymmetry. What are the potential causes and how can I fix this?
A1: Asymmetrical peak shapes can significantly impact the accuracy of your frequency and intensity measurements. The common causes and their solutions are outlined below:
-
Cause 1: Column Overload (in systems with a chromatographic component).
-
Cause 2: Incorrect Mobile Phase Composition.
-
Solution: The composition of the mobile phase can affect peak shape. Adjusting the solvent composition, pH, or buffer concentration can improve symmetry. For instance, increasing the organic solvent content can reduce peak tailing.[2]
-
-
Cause 3: Column Degradation or Voids.
-
Solution: Over time, the chromatography column can degrade or develop voids, leading to asymmetrical peaks.[2] If you suspect this, try replacing the column with a new one.
-
-
Cause 4: High Sample Viscosity.
-
Solution: A sample that is too viscous can result in tailing peaks.[1] Diluting the sample can help to mitigate this issue.
-
Issue: Poor Signal-to-Noise Ratio (SNR)
Q2: The signal-to-noise ratio in my spectra is very low, making it difficult to identify real peaks. What steps can I take to improve it?
A2: A low signal-to-noise ratio (SNR) can obscure weak signals and lead to inaccurate data interpretation. Here are several techniques to enhance your SNR:
-
Signal Averaging: This is a powerful software-based approach. By acquiring and averaging multiple scans of your spectrum, the random noise will decrease, while the coherent signal will be reinforced. The SNR improves by the square root of the number of scans averaged.[4][5]
-
Hardware Optimization:
-
Increase Light Source Intensity: A stronger microwave source can lead to a stronger signal.
-
Use a Larger Diameter Fiber: If your setup uses fiber optics, a larger diameter fiber can deliver more microwave power to the sample.[5]
-
Increase Detector Integration Time: A longer integration time allows the detector to collect more signal. However, be aware that this can also increase certain types of noise if the detector is not cooled.[5][6]
-
-
Electronic Filtering:
-
Low-Pass Filters: These electronic circuits can be used to remove high-frequency noise while allowing the lower-frequency signal to pass.[7]
-
-
Modulation Techniques: For low-frequency signals where flicker noise is significant, modulating the signal to a higher frequency can be effective. After filtering out the low-frequency noise, the signal is demodulated back to its original frequency.[7]
A troubleshooting workflow for improving a poor signal-to-noise ratio is illustrated in the diagram below.
SNR Improvement Workflow
FAQs on Calibration Techniques
This section answers frequently asked questions about the calibration of high-precision microwave spectrometers.
Q3: What is frequency calibration and why is it crucial?
A3: Frequency calibration is the process of ensuring that the frequency axis of your spectrometer is accurate. It is crucial because microwave spectroscopy relies on the precise measurement of rotational transition frequencies to identify molecules and determine their structure.[8][9] Inaccurate frequency calibration will lead to misidentification of compounds and incorrect structural parameters.
Q4: How do I perform a frequency calibration?
A4: A common method for frequency calibration involves using a well-characterized standard gas with known rotational transition frequencies. Carbonyl Sulfide (OCS) is a widely used calibrant due to its strong, well-defined spectral lines. The general procedure is as follows:
-
Introduce a low-pressure sample of the calibrant gas (e.g., OCS) into the spectrometer.
-
Acquire the spectrum of the calibrant.
-
Compare the measured frequencies of the known transitions with their literature values.
-
Generate a calibration curve or correction factor to apply to your experimental spectra.
Q5: What is intensity calibration and why is it important?
A5: Intensity calibration ensures that the measured peak intensities accurately reflect the abundance of the species or the strength of the transition.[10] The raw data from a spectrometer is often distorted by the frequency-dependent response of its components (e.g., detector, amplifiers). Intensity calibration corrects for these instrumental artifacts, allowing for reliable quantitative analysis and comparison of spectral data.[10]
Q6: What is baseline correction and what are the common methods?
A6: Baseline correction is a crucial preprocessing step that removes unwanted background signals and instrumental drift from a spectrum. A distorted baseline can obscure real peaks and lead to inaccurate intensity measurements. Several algorithms are used for baseline correction, with some of the most common being:
-
Asymmetric Least Squares (ALS): This method iteratively fits a smooth baseline to the spectrum while penalizing points that are above the curve (i.e., the peaks).
-
Wavelet Transform: This technique decomposes the spectrum into different frequency components, allowing for the separation and removal of the broad, low-frequency baseline features from the sharp, high-frequency peaks.
The choice of method can depend on the nature of the baseline distortion and the spectral features.
Data Presentation
Table 1: Comparison of Baseline Correction Algorithms
| Algorithm | Principle | Advantages | Disadvantages |
| Asymmetric Least Squares (ALS) | Iteratively fits a smoothed baseline, penalizing peaks. | Generally robust and effective for a variety of baseline shapes. | May require careful tuning of parameters (smoothness and asymmetry). |
| Wavelet Transform | Decomposes the signal into different frequency components to separate baseline from peaks. | Can be effective for complex baselines and is less sensitive to peak widths. | May introduce artifacts if not properly optimized. |
| Polynomial Fitting | Fits a polynomial function to the baseline points of the spectrum. | Simple to implement and computationally fast. | Can be inaccurate for complex, non-polynomial baselines. |
Table 2: Techniques for Signal-to-Noise Ratio (SNR) Enhancement
| Technique | Description | Expected SNR Improvement | Key Considerations |
| Signal Averaging | Multiple spectra are acquired and averaged.[4][5] | Proportional to the square root of the number of scans. | Increases measurement time. |
| Increased Integration Time | The detector collects signal for a longer period.[5][6] | Can increase signal level. | May also increase detector noise; potential for saturation. |
| Low-Pass Filtering | Electronic or digital filtering to remove high-frequency noise.[7] | Dependent on the noise characteristics and filter parameters. | Can distort sharp spectral features if the filter is too aggressive. |
Experimental Protocols
Protocol 1: Frequency Calibration using Carbonyl Sulfide (OCS)
Objective: To accurately calibrate the frequency axis of the microwave spectrometer.
Materials:
-
High-precision microwave spectrometer
-
Cylinder of Carbonyl Sulfide (OCS) gas (high purity)
-
Vacuum system
-
Pressure gauge
Procedure:
-
Evacuate the spectrometer's sample cell to a low pressure (e.g., < 10⁻⁵ mbar).
-
Introduce a small amount of OCS gas into the sample cell. The pressure should be low enough to avoid significant pressure broadening of the spectral lines (typically in the range of a few mTorr).
-
Set the spectrometer to scan over a frequency range that includes known rotational transitions of OCS.
-
Acquire the spectrum, ensuring a good signal-to-noise ratio. Signal averaging may be necessary.
-
Identify several well-resolved rotational transitions of OCS in the acquired spectrum.
-
Compare the measured center frequencies of these transitions with the highly accurate literature values for OCS.
-
Calculate the difference between the measured and literature frequencies for each line.
-
If a systematic offset is observed, apply a correction to the spectrometer's frequency synthesizer or in the data processing software. For a frequency-dependent error, a polynomial correction may be necessary.
-
Verify the calibration by re-measuring the OCS spectrum and confirming that the measured frequencies match the literature values within the desired accuracy.
The logical workflow for this frequency calibration protocol is depicted below.
Frequency Calibration Workflow
Microwave Spectroscopy in Drug Development
Q7: How is high-precision microwave spectroscopy utilized in drug development?
A7: High-precision microwave spectroscopy is a powerful tool in drug discovery and development, primarily due to its ability to provide detailed information about molecular structure and conformation. Here are some key applications:
-
Structural Biology: Microwave spectroscopy can determine the precise three-dimensional structure of small molecules, including potential drug candidates. This information is crucial for understanding how a drug interacts with its biological target.
-
Conformational Analysis: Many drug molecules are flexible and can exist in multiple conformations. Microwave spectroscopy can identify the preferred conformations of a molecule in the gas phase, providing insights into its bioactive shape.
-
Pharmaceutical Formulation: The technique can be used to study the properties of solid-state materials, which is relevant for understanding the stability and dissolution of drug formulations.
-
Process Analytical Technology (PAT): In some cases, microwave spectroscopy can be used for real-time monitoring of chemical reactions during drug synthesis, ensuring quality and consistency.[5]
References
- 1. oceanoptics.com [oceanoptics.com]
- 2. spectroscopyasia.com [spectroscopyasia.com]
- 3. Signal-to-Noise Ratio (SNR) in Spectroscopy: Photon Shot Noise vs Detector Noise [eureka.patsnap.com]
- 4. Building diagrams using graphviz | Chad’s Blog [chadbaldwin.net]
- 5. meetings.iac.es [meetings.iac.es]
- 6. phys.ubbcluj.ro [phys.ubbcluj.ro]
- 7. electrooptics.com [electrooptics.com]
- 8. Automated Wavelength and Intensity Calibration Significantly Improves Spectral Accuracy | Teledyne Vision Solutions [teledynevisionsolutions.com]
- 9. Troubleshooting [chem.rochester.edu]
- 10. graphviz.org [graphviz.org]
addressing instrumental artifacts in rotational spectra analysis
Welcome to the Technical Support Center for Rotational Spectra Analysis. This resource is designed for researchers, scientists, and drug development professionals to troubleshoot and resolve common instrumental artifacts encountered during their experiments.
Frequently Asked Questions (FAQs)
Q1: What are the most common instrumental artifacts in rotational spectra?
A1: The most common instrumental artifacts include baseline drift, inconsistent peak intensities, electronic noise, phase errors (especially in Fourier Transform Microwave spectroscopy), and standing waves. These can arise from various sources including thermal instability, electronic malfunctions, improper calibration, and reflections within the spectrometer.[1][2][3]
Q2: How can I distinguish between a real spectral feature and an artifact?
A2: Real spectral features are reproducible under consistent experimental conditions and typically fit known theoretical models of rotational transitions. Artifacts, on the other hand, may appear as random noise, broad baseline distortions, or sharp, non-physical peaks that do not correspond to expected molecular transitions.[2] Comparing your spectrum to a blank or reference spectrum can also help identify instrument-related issues.[2]
Q3: Can environmental factors affect my rotational spectra?
A3: Yes, environmental factors can significantly impact spectral quality. Temperature fluctuations can cause baseline drift and affect the population of rotational states, influencing peak intensities.[4][5] Pressure variations can lead to line broadening.[5][6] Vibrations and electromagnetic interference from nearby equipment can also introduce noise.[2]
Troubleshooting Guides
This section provides detailed troubleshooting for specific issues you may encounter.
Issue 1: Baseline Drift or Instability
Symptom: The baseline of your spectrum is not flat but shows a continuous upward or downward trend, or wanders over time.[1][2]
Possible Causes and Solutions:
| Cause | Solution |
| Thermal Instability: The spectrometer components, especially the detector and electronics, have not reached thermal equilibrium.[2] | Allow the instrument to warm up for a sufficient period (typically 30-60 minutes) before acquiring data. Ensure a stable laboratory temperature. |
| Detector Saturation: The detector is saturated by a very strong signal. | Reduce the signal intensity by decreasing the sample concentration or the source power. |
| Contamination: Contaminants in the sample cell or on optical components can cause a drifting baseline.[7] | Clean the sample cell and any accessible optical components according to the manufacturer's instructions. |
| Electronic Drift: Aging electronic components can cause a slow drift in the baseline. | If the problem persists after addressing other causes, the instrument may require servicing by a qualified technician. |
Issue 2: Inconsistent or Inaccurate Peak Intensities
Symptom: The relative intensities of your rotational transitions are not consistent between measurements or do not match theoretical predictions.
Possible Causes and Solutions:
| Cause | Solution |
| Improper Spectrometer Calibration: The intensity response of the spectrometer has not been correctly calibrated.[8][9] | Perform an intensity calibration using a standard sample with known rotational line intensities. |
| Temperature Fluctuations: Changes in the sample temperature affect the Boltzmann distribution of rotational states, leading to variations in peak intensities. | Ensure the sample cell is at a stable and well-controlled temperature. |
| Pressure Fluctuations: Changes in sample pressure can affect line widths and, consequently, peak heights. | Maintain a stable and accurately measured pressure in the sample cell. |
| Non-linear Detector Response: The detector's response is not linear over the dynamic range of the signal. | Operate within the linear range of the detector. This may require adjusting the sample concentration or signal attenuation. |
Issue 3: Presence of Electronic Noise
Symptom: The spectrum exhibits random, high-frequency fluctuations or sharp, spurious peaks.[3]
Possible Causes and Solutions:
| Cause | Solution |
| Electromagnetic Interference (EMI): Noise from nearby electronic equipment is interfering with the spectrometer's electronics.[3] | Ensure the spectrometer is properly grounded. If possible, move interfering equipment away from the spectrometer or use EMI shielding. |
| Improper Grounding: A ground loop or improper grounding of the spectrometer or associated electronics. | Check all grounding connections and ensure a single, high-quality ground point is used. |
| Shot Noise: Random fluctuations in the electric current within the detector and electronics.[10] | Increase the signal averaging time. For very weak signals, a more sensitive detector may be required. |
| Faulty Electronic Components: A failing electronic component within the spectrometer can introduce noise. | If the noise is persistent and other causes have been ruled out, professional servicing may be necessary. |
Issue 4: Phase Errors in FTMW Spectroscopy
Symptom: In Fourier Transform Microwave (FTMW) spectra, peaks appear distorted, with negative lobes or asymmetric shapes.[11][12][13]
Possible Causes and Solutions:
| Cause | Solution |
| Incorrect Phase Correction Algorithm: The software's phase correction routine is not being applied correctly.[11][12] | Most modern spectroscopy software has automatic phase correction. If this fails, manual phase correction can be applied. This typically involves adjusting a zero-order and a first-order phase parameter to achieve a pure absorption lineshape.[14][15] |
| Dispersion in the Spectrometer: Frequency-dependent phase shifts are introduced by the electronic components and the sample cell.[12] | A proper phase correction routine should account for these dispersive effects. |
| Timing Errors in Data Acquisition: Inaccuracies in the timing of the free induction decay (FID) acquisition. | Ensure the data acquisition system is functioning correctly and that timing parameters are set appropriately. |
Issue 5: Standing Waves and Reflections
Symptom: The baseline of the spectrum shows a periodic, sinusoidal-like oscillation.
Possible Causes and Solutions:
| Cause | Solution |
| Reflections between Optical Components: Microwave radiation reflects between components in the spectrometer, creating standing waves. | Place microwave-absorbing material at strategic points in the spectrometer to dampen reflections. Ensure all connections are properly matched to minimize impedance mismatches. |
| Reflections from the Sample Cell: Reflections can occur at the windows or walls of the sample cell. | Use anti-reflection coated windows and a well-designed sample cell to minimize internal reflections. |
Experimental Protocols
Protocol 1: Baseline Correction Procedure
-
Warm-up: Allow the spectrometer to warm up for at least 60 minutes to ensure thermal stability.
-
Acquire Blank Spectrum: Record a spectrum with an empty sample cell or under high vacuum. This will capture the instrument's baseline response.
-
Acquire Sample Spectrum: Introduce the sample and acquire the rotational spectrum under the same conditions as the blank.
-
Subtract Blank: Subtract the blank spectrum from the sample spectrum. This will remove many of the baseline features that are intrinsic to the instrument.
-
Polynomial Fitting (if necessary): If a residual baseline drift remains, use a polynomial fitting algorithm to model and subtract the remaining baseline. Be cautious not to over-fit and distort the real spectral lines.[1]
Protocol 2: Spectrometer Calibration for Accurate Intensities
-
Select a Calibration Standard: Choose a well-characterized molecule with known rotational transition frequencies and intensities in the frequency range of interest (e.g., OCS, SO2).
-
Prepare a Dilute Sample: Prepare a low-pressure gaseous sample of the calibration standard to avoid pressure broadening effects.
-
Acquire the Spectrum: Record the rotational spectrum of the calibration standard.
-
Compare with Literature Values: Compare the measured relative intensities of the rotational transitions to the known literature values.
-
Generate a Correction Curve: Create a frequency-dependent intensity correction curve based on the differences between the measured and literature values.
-
Apply Correction: Apply this correction curve to subsequently measured spectra of your samples to obtain accurate relative intensities.[16][8]
Quantitative Data Summary
The following table provides typical values for common instrumental artifacts. These are illustrative and can vary significantly depending on the specific instrument and experimental conditions.
| Artifact | Typical Magnitude/Frequency | Notes |
| Baseline Drift | 1-5% of full scale over a 1 GHz scan | Highly dependent on thermal stability.[1] |
| Electronic Noise (White Noise) | 0.1-1% RMS of signal intensity | Can be reduced by signal averaging. |
| Electronic Noise (Spurious Peaks) | Can be narrow and intense | Often appears at specific frequencies related to power lines (e.g., 50/60 Hz and their harmonics). |
| Temperature-Induced Intensity Variation | 1-2% per degree Celsius | Varies with the rotational constant of the molecule. |
| Pressure Broadening | 10-100 kHz/mTorr | Highly dependent on the molecule and collision partner. |
Visual Troubleshooting Guides
Workflow for Identifying and Correcting Baseline Drift
References
- 1. Origins of Baseline Drift and Distortion in Fourier Transform Spectra - PMC [pmc.ncbi.nlm.nih.gov]
- 2. azooptics.com [azooptics.com]
- 3. News - What is noise in spectrometer? [jinsptech.com]
- 4. quora.com [quora.com]
- 5. Atmospheric Pressure Plasma for Carbon Material Modification and Synthesis: A Comprehensive Review [mdpi.com]
- 6. repository.rice.edu [repository.rice.edu]
- 7. Automated Wavelength and Intensity Calibration Significantly Improves Spectral Accuracy | Teledyne Vision Solutions [teledynevisionsolutions.com]
- 8. How to Calibrate a Spectrometer: 5 Common Questions Answered [jxaiyi.com]
- 9. astronomy.stackexchange.com [astronomy.stackexchange.com]
- 10. Shot noise - Wikipedia [en.wikipedia.org]
- 11. mdpi.com [mdpi.com]
- 12. researchgate.net [researchgate.net]
- 13. mdpi.com [mdpi.com]
- 14. Phase Correction with Mnova [mestrelabcn.com]
- 15. docs.nmrium.org [docs.nmrium.org]
- 16. researchgate.net [researchgate.net]
Validation & Comparative
A Researcher's Guide to Validating Rotational Constants with Ab Initio Calculations
For researchers, scientists, and drug development professionals, the precise determination of molecular structures is paramount. Rotational spectroscopy provides highly accurate experimental data on the rotational constants of a molecule, which are intrinsically linked to its moments of inertia and, therefore, its three-dimensional structure. The validation of theoretical models against this experimental data is a critical step in computational chemistry. This guide provides a comprehensive comparison of ab initio methods for calculating rotational constants, supported by experimental data and detailed protocols.
The Synergy Between Theory and Experiment
The validation of rotational constants derived from ab initio calculations against those determined experimentally through rotational spectroscopy serves as a powerful benchmark for the accuracy of theoretical methods.[1][2] This synergy is a cornerstone of modern structural chemistry, enabling the refinement of computational models and providing a deeper understanding of molecular properties. Experimental techniques like microwave spectroscopy and high-resolution infrared spectroscopy yield rotational constants with exceptional precision, often to within a few kilohertz.[2][3] These highly accurate experimental values then serve as the "gold standard" for assessing the performance of various ab initio approaches.
The process typically involves a feedback loop where initial ab initio calculations guide the search for and assignment of spectral lines in experimental rotational spectra.[3] Conversely, the experimentally determined rotational constants are used to benchmark and validate the computational methods, leading to improved predictive power for molecules that are difficult to study experimentally.
Comparison of Ab Initio Methods for Rotational Constant Prediction
The accuracy of ab initio calculations of rotational constants is highly dependent on the chosen level of theory and basis set. A variety of methods are available, each with its own trade-offs between computational cost and accuracy. Coupled-cluster methods, particularly CCSD(T) (Coupled Cluster with Singles, Doubles, and perturbative Triples), are often considered the "gold standard" for their high accuracy, though they are computationally expensive.[4][5] Density Functional Theory (DFT) offers a range of functionals that provide a good balance of accuracy and computational efficiency, making them suitable for larger molecules.[6][7][8] Møller-Plesset perturbation theory, especially at the second order (MP2), also provides a reliable method for calculating rotational constants.[9]
Below is a summary of the performance of various ab initio methods in predicting rotational constants, presented as the mean absolute error (MAE) in MHz and the percentage error relative to experimental values for a set of benchmark molecules.
| Level of Theory | Basis Set | Mean Absolute Error (MHz) | Mean Absolute Percentage Error (%) |
| Hartree-Fock (HF) | cc-pVTZ | 150 - 300 | 1.0 - 2.0 |
| MP2 | cc-pVTZ | 30 - 100 | 0.2 - 0.7 |
| B3LYP | cc-pVTZ | 20 - 80 | 0.15 - 0.5 |
| PBE0 | cc-pVTZ | 25 - 90 | 0.2 - 0.6 |
| M06-2X | cc-pVTZ | 15 - 60 | 0.1 - 0.4 |
| CCSD(T) | cc-pVTZ | 5 - 20 | < 0.1 |
| CCSD(T) | cc-pVQZ | 2 - 10 | < 0.05 |
Note: The accuracy can vary depending on the specific molecule and the inclusion of vibrational corrections.
The Importance of Vibrational Corrections
A direct comparison between calculated equilibrium rotational constants (Be) and experimentally determined ground-state rotational constants (B0) is not entirely accurate. This is because experimental measurements are made on molecules in their ground vibrational state, which has a zero-point vibrational energy that slightly alters the effective molecular geometry. Therefore, to achieve high accuracy, it is crucial to account for these vibrational effects.[10][11]
The relationship between the equilibrium and ground-state rotational constants is given by:
B0 = Be - ½ Σ αrB
where αrB are the vibration-rotation interaction constants. These constants can be calculated using ab initio methods, typically through second-order vibrational perturbation theory (VPT2).[4][12] The inclusion of these corrections significantly improves the agreement between theoretical and experimental rotational constants.[10][11] For semi-rigid molecules, the vibrational contribution to the rotational constants is typically between 0.1% and 0.7% of the equilibrium value.[4][10]
Experimental and Computational Protocols
Experimental Determination of Rotational Constants via Microwave Spectroscopy
Microwave spectroscopy is a high-resolution technique used to measure the absorption of microwave radiation by molecules in the gas phase, corresponding to transitions between rotational energy levels.[13]
Methodology:
-
Sample Preparation: The molecule of interest is introduced into the gas phase at low pressure (typically a few millitorr) within a sample cell. For less volatile compounds, heating or supersonic expansion techniques may be used.[13]
-
Instrumentation: A typical microwave spectrometer consists of a microwave source (e.g., a Gunn diode or backward-wave oscillator), a sample cell, a detector (e.g., a Schottky diode), and a data acquisition system.[13] Fourier-transform microwave (FTMW) spectroscopy is a powerful variant that offers high sensitivity and resolution.[13][14]
-
Data Acquisition: The frequency of the microwave radiation is swept over a range, and the absorption of radiation by the sample is recorded as a function of frequency.
-
Spectral Analysis: The resulting spectrum consists of a series of sharp absorption lines. These lines are assigned to specific rotational transitions (J' ← J'').
-
Fitting and Determination of Rotational Constants: The frequencies of the assigned transitions are fitted to a Hamiltonian model, such as the rigid rotor model with centrifugal distortion corrections. This fitting procedure yields highly precise values for the rotational constants (A, B, and C) and centrifugal distortion constants.[13][15]
Ab Initio Calculation of Rotational Constants
Computational quantum chemistry software packages, such as Gaussian, are widely used to calculate rotational constants.[16][17][18]
Methodology:
-
Geometry Optimization: The first step is to find the equilibrium geometry of the molecule. This is achieved by performing a geometry optimization calculation at a chosen level of theory and basis set (e.g., B3LYP/cc-pVTZ or CCSD(T)/aug-cc-pVTZ). The optimization should converge to a stationary point on the potential energy surface, which is confirmed by a frequency calculation showing no imaginary frequencies.
-
Frequency Calculation: A frequency calculation at the optimized geometry is then performed. This calculation provides the moments of inertia from which the equilibrium rotational constants (Be) are derived.
-
Vibrational Corrections: To obtain the ground-state rotational constants (B0) for direct comparison with experimental data, vibrational corrections must be calculated. This is typically done by requesting an anharmonic frequency calculation (e.g., Freq=VibRot in Gaussian), which computes the vibration-rotation interaction constants (αr).[16]
-
Calculation of B0: The software will then use the calculated αr values to compute the B0 values.
-
Output Analysis: The output file will contain the calculated equilibrium and ground-state rotational constants, typically in units of GHz or MHz. The Output=Pickett keyword in Gaussian can be useful for obtaining the spectroscopic parameters in a format suitable for spectral fitting programs.[16]
Visualizing the Validation Workflow
The process of validating ab initio rotational constants with experimental data can be visualized as a logical workflow.
Caption: Workflow for validating ab initio rotational constants.
Logical Relationship between Key Concepts
The determination and validation of rotational constants involve a hierarchical relationship between theoretical concepts and experimental observations.
Caption: Relationship between molecular structure and rotational spectroscopy.
By carefully selecting appropriate ab initio methods and accounting for vibrational effects, researchers can accurately predict rotational constants that are in excellent agreement with experimental data. This validation process not only confirms the accuracy of the computed molecular structure but also provides valuable insights for the interpretation of complex rotational spectra.
References
- 1. Connections between the accuracy of rotational constants and equilibrium molecular structures - Physical Chemistry Chemical Physics (RSC Publishing) [pubs.rsc.org]
- 2. undergradresearch.chem.wisc.edu [undergradresearch.chem.wisc.edu]
- 3. McGuire Research Group [mcguirelab.mit.edu]
- 4. mdpi.com [mdpi.com]
- 5. pubs.acs.org [pubs.acs.org]
- 6. pubs.aip.org [pubs.aip.org]
- 7. Benchmarking quantum chemical methods for accurate gas-phase structure predictions of carbonyl compounds: the case of ethyl butyrate - Physical Chemistry Chemical Physics (RSC Publishing) DOI:10.1039/D2CP05774C [pubs.rsc.org]
- 8. comporgchem.com [comporgchem.com]
- 9. Ab Initio Rotational and Vibrational Spectroscopy of C3H5 Radicals at the Coupled Cluster Level - PMC [pmc.ncbi.nlm.nih.gov]
- 10. Connections between the accuracy of rotational constants and equilibrium molecular structures - Physical Chemistry Chemical Physics (RSC Publishing) DOI:10.1039/D2CP04706C [pubs.rsc.org]
- 11. trygvehelgaker.no [trygvehelgaker.no]
- 12. pubs.acs.org [pubs.acs.org]
- 13. fiveable.me [fiveable.me]
- 14. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 15. pubs.aip.org [pubs.aip.org]
- 16. Gaussian Recipes for Rotational Spectroscopy [laserkelvin.github.io]
- 17. researchgate.net [researchgate.net]
- 18. gaussian.com [gaussian.com]
A Comparative Guide to Experimental and Theoretical Rotational Spectra
For Researchers, Scientists, and Drug Development Professionals
Rotational spectroscopy is a high-resolution technique that provides a wealth of information about the structure, bonding, and dynamics of molecules in the gas phase.[1][2] By probing the transitions between quantized rotational energy levels, researchers can determine molecular properties with exceptional precision. This guide offers a comprehensive comparison between experimental and theoretical approaches to rotational spectroscopy, highlighting their respective methodologies, data outputs, and the synergistic relationship that drives modern molecular science.
Experimental Methodologies: Probing Molecular Rotations
The primary goal of experimental rotational spectroscopy is to measure the frequencies of electromagnetic radiation that are absorbed or emitted by a molecule as it transitions between rotational energy levels.[1] The resulting spectrum is a unique fingerprint of the molecule's moments of inertia.
Key Experimental Techniques
-
Microwave Spectroscopy: This is the most common technique for observing pure rotational transitions.[1][2] It is applicable to molecules with a permanent electric dipole moment.[3] The interaction between this dipole moment and the oscillating electric field of the microwave radiation induces the transitions. Modern microwave spectrometers, particularly Fourier Transform Microwave (FTMW) spectrometers, offer incredibly high resolution and sensitivity, allowing for the study of weakly bound complexes and molecules with low volatility.
-
Far-Infrared Spectroscopy: This technique can also be used to measure rotational spectra, particularly for light molecules where the rotational transitions fall into the far-infrared region of the electromagnetic spectrum.[1]
-
Raman Spectroscopy: For non-polar molecules, which lack a permanent dipole moment and are therefore transparent to microwaves, rotational spectra can be obtained using Raman spectroscopy.[1] This method relies on the scattering of light by the molecule and is sensitive to the anisotropy of the molecule's polarizability.
Experimental Protocol: A Generalized Workflow
A typical rotational spectroscopy experiment involves the following steps:
-
Sample Preparation: The molecule of interest is introduced into the gas phase, often at very low pressures to minimize intermolecular interactions. This can be achieved through gentle heating for volatile compounds or by using techniques like laser ablation for less volatile solids.
-
Microwave Irradiation: A pulse of microwave radiation is directed into the sample chamber. In broadband techniques, this pulse contains a wide range of frequencies.
-
Signal Detection: After the excitation pulse, the coherently rotating molecules emit a faint microwave signal (free induction decay). This signal is detected by a sensitive receiver.
-
Data Processing: The time-domain signal is converted into a frequency-domain spectrum using a Fourier transform. This spectrum reveals the frequencies of the rotational transitions.
-
Spectral Analysis: The measured transition frequencies are then fitted to a quantum mechanical model to determine the molecule's rotational constants and other spectroscopic parameters.
Theoretical Methodologies: Predicting Molecular Rotations
Theoretical calculations are indispensable for interpreting and predicting rotational spectra. They provide the initial parameters for spectral searches and are crucial for understanding the underlying molecular structure and dynamics.
The Rigid Rotor Approximation and Beyond
The simplest theoretical model is the rigid rotor , where the bond lengths and angles of the molecule are assumed to be fixed.[4] The rotational energy levels of a diatomic molecule in this model are given by:
EJ = B * J(J+1)
where B is the rotational constant and J is the rotational quantum number.
In reality, molecules are not rigid. As a molecule rotates, centrifugal forces can cause the bonds to stretch slightly. This effect, known as centrifugal distortion , is accounted for by adding further terms to the energy level expression.[1] More sophisticated models also include corrections for fine and hyperfine structure, and Coriolis coupling.[1]
Quantum Chemical Calculations
Modern computational chemistry provides powerful tools for predicting rotational constants from first principles. The general workflow is as follows:
-
Geometry Optimization: The first step is to calculate the equilibrium geometry of the molecule using high-level quantum chemical methods, such as coupled-cluster theory or density functional theory (DFT).
-
Calculation of Rotational Constants: From the optimized geometry, the moments of inertia and subsequently the equilibrium rotational constants (Be) are calculated.
-
Vibrational Corrections: To accurately compare with experimental values, which are measured in the ground vibrational state (B0), vibrational corrections must be included in the theoretical calculations.
The accuracy of these calculations is highly dependent on the level of theory and the basis set used.
Data Presentation: A Comparative Case Study of Carbon Monoxide (CO)
Carbon monoxide is a simple diatomic molecule that has been extensively studied by both experimental and theoretical methods. The table below compares the experimental rotational constant (B0) and bond length (r0) with values obtained from theoretical calculations.
| Parameter | Experimental Value | Theoretical Value (Example Calculation) |
| Rotational Constant (B0) | 1.922529 cm-1 | Varies with method; high-level calculations can achieve <0.1% error |
| Bond Length (r0) | 1.128323 Å | Varies with method; high-level calculations can achieve high accuracy |
Note: The accuracy of theoretical values is highly dependent on the chosen computational method and basis set.
The Synergy Between Experiment and Theory
The comparison of experimental and theoretical rotational spectra is a powerful approach in modern chemistry.
As the diagram illustrates, theoretical predictions guide experimental searches for spectral lines. In turn, experimental data are used to benchmark and refine theoretical models. This iterative process leads to a more accurate and complete understanding of molecular structure and properties. For complex molecules, theoretical calculations are often essential for assigning the dense and complicated rotational spectra.
References
Cross-Validation of Spectroscopic Data: A Comparative Guide for Researchers
In the realm of scientific research and drug development, the accuracy and reliability of experimental data are paramount. Spectroscopic techniques are powerful tools for elucidating molecular structures and quantifying substances, but their findings are often strengthened through cross-validation with orthogonal experimental methods. This guide provides an objective comparison of the performance of various spectroscopic techniques with alternative methods, supported by experimental data, detailed protocols, and visual workflows to aid researchers, scientists, and drug development professionals in their analytical endeavors.
Quantitative Data Presentation: A Side-by-Side Comparison
The following tables summarize quantitative data from various studies, offering a clear comparison of spectroscopic methods with other analytical techniques.
Table 1: Comparison of UV-Visible Spectroscopy and High-Performance Liquid Chromatography (HPLC) for the Quantification of Repaglinide (B1680517) in Tablets
| Parameter | UV-Visible Spectroscopy | HPLC |
| Linearity Range (µg/mL) | 5-30 | 5-50 |
| Correlation Coefficient (r²) | > 0.999 | > 0.999 |
| Precision (% RSD) | < 1.50 | < 1.50 |
| Mean Recovery (%) | 99.63 - 100.45 | 99.71 - 100.25 |
Source: Data compiled from a comparative study on the determination of repaglinide in tablets[1]. This table demonstrates that both UV-Vis spectroscopy and HPLC exhibit excellent linearity and precision for the quantification of repaglinide, with HPLC showing a slightly better recovery range[1].
Table 2: Comparison of Near-Infrared (NIR) Spectroscopy and UV Assay for Tablet Content Uniformity
| Parameter | NIR Spectroscopy | UV Assay |
| Mean %API Difference | 2.32% | - |
| Maximum %API Difference | 4.29% | - |
| Mean Range of API Content Difference | 2.85% | - |
| Maximum Range of API Content Difference | 6.28% | - |
| Standard Error of Calibration (SEC) | 1.13 mg | - |
| Standard Error of Prediction (SEP) | 1.36 mg | - |
Source: Data from studies on the high-throughput analysis of pharmaceutical tablet content uniformity[2][3]. These results indicate a good agreement between NIR spectroscopy and the standard UV assay for determining the active pharmaceutical ingredient (API) content in tablets[2].
Table 3: Comparison of Mass Spectrometry and ELISA for Protein Quantification
| Parameter | Mass Spectrometry (Targeted Proteomics) | Enzyme-Linked Immunosorbent Assay (ELISA) |
| Correlation (R) | 0.97 (in a comparative study) | - |
| Sensitivity | High, capable of detecting low abundant proteins | High, with a larger dynamic range |
| Throughput | Can be high with automation | High, suitable for large sample numbers |
| Sample Preparation | Complex | Simpler |
Source: Data from a platform cross-validation study of immunoaffinity mass spectrometry versus ELISA and a review on protein quantitation methods[4]. This comparison highlights the strong correlation between the two methods, with mass spectrometry offering detailed molecular information and ELISA providing a simpler, high-throughput workflow for targeted protein quantification[4].
Table 4: Comparison of Quantitative NMR (qNMR) and HPLC for Purity Assessment
| Parameter | Quantitative NMR (qNMR) | HPLC |
| Principle | Quantification based on the direct proportionality between signal integral and the number of nuclei. | Separation based on differential partitioning between a stationary and mobile phase. |
| Universality | Applicable to nearly all organic molecules with NMR-active nuclei. | Requires a chromophore for UV detection; other detectors are available. |
| Selectivity | Excellent for structural confirmation and identification of impurities. | High selectivity for separating structurally similar impurities. |
| Sensitivity | Generally lower than HPLC, but can be enhanced. | Generally offers higher sensitivity for trace impurity analysis. |
Source: Information compiled from a comparative guide on purity validation[5][6][7]. This table illustrates the orthogonal nature of qNMR and HPLC, with qNMR providing absolute quantification and structural information, while HPLC excels in separation and sensitivity[7].
Experimental Protocols
Detailed methodologies are crucial for the reproducibility and validation of experimental results. Below are generalized protocols for key experiments cited in the comparative data.
Protocol 1: Cross-Validation of a Spectroscopic Method (e.g., UV-Vis) with a Chromatographic Method (e.g., HPLC) for Drug Quantification
-
Objective: To validate the accuracy and precision of a UV-Vis spectrophotometric method for the quantification of an active pharmaceutical ingredient (API) in a tablet formulation against a validated HPLC method.
-
Materials:
-
API reference standard
-
Tablet formulation containing the API
-
Solvents and reagents for both UV-Vis and HPLC analysis
-
Calibrated UV-Vis spectrophotometer and HPLC system
-
-
Method Validation Parameters (as per ICH guidelines):
-
Specificity: Analyze the drug substance, placebo, and a mixture to ensure no interference from excipients at the analytical wavelength for UV-Vis and at the retention time for HPLC.
-
Linearity: Prepare a series of standard solutions of the API at different concentrations (e.g., 5-30 µg/mL). For UV-Vis, measure the absorbance at the wavelength of maximum absorption (λmax). For HPLC, inject the standards and record the peak area. Plot a calibration curve of absorbance/peak area versus concentration and determine the correlation coefficient (r²).
-
Precision:
-
Repeatability (Intra-day precision): Analyze multiple preparations of the same sample on the same day and calculate the relative standard deviation (%RSD).
-
Intermediate Precision (Inter-day precision): Analyze the same sample on different days by different analysts to assess the method's robustness.
-
-
Accuracy (Recovery): Perform recovery studies by spiking a known amount of the API into the placebo at different concentration levels (e.g., 80%, 100%, 120%). Analyze the samples and calculate the percentage recovery.
-
-
Cross-Validation Procedure:
-
Prepare a set of tablet samples for analysis.
-
Analyze each sample using both the developed UV-Vis method and the validated HPLC method.
-
Statistically compare the quantitative results obtained from both methods (e.g., using a t-test) to determine if there is a significant difference between the two methods.
-
Protocol 2: Cross-Validation of Mass Spectrometry with ELISA for Protein Quantification
-
Objective: To cross-validate the quantification of a target protein in a biological matrix using a targeted mass spectrometry-based assay and a sandwich ELISA.
-
Materials:
-
Biological samples (e.g., plasma, cell lysate)
-
Recombinant protein standard of the target protein
-
Antibodies for ELISA (capture and detection)
-
Reagents for protein digestion and peptide purification for mass spectrometry
-
Calibrated mass spectrometer (e.g., LC-MS/MS) and ELISA plate reader
-
-
Mass Spectrometry (Targeted Proteomics) Protocol:
-
Sample Preparation: Spike a known amount of a stable isotope-labeled internal standard peptide into the samples. Perform protein digestion (e.g., with trypsin) to generate peptides.
-
LC-MS/MS Analysis: Separate the peptides using liquid chromatography and detect and quantify the target peptide and its internal standard using selected reaction monitoring (SRM) or multiple reaction monitoring (MRM) on the mass spectrometer.
-
Quantification: Calculate the concentration of the target protein based on the ratio of the peak areas of the endogenous peptide to the internal standard peptide.
-
-
ELISA Protocol:
-
Assay Procedure: Coat a 96-well plate with the capture antibody. Add the biological samples and standards to the wells. Add the detection antibody, followed by a substrate to generate a colorimetric signal.
-
Quantification: Measure the absorbance using a plate reader and determine the concentration of the target protein in the samples by interpolating from a standard curve generated using the recombinant protein standard.
-
-
Cross-Validation Analysis:
-
Analyze the same set of biological samples using both the mass spectrometry and ELISA methods.
-
Perform a correlation analysis (e.g., Pearson correlation) to assess the agreement between the quantitative results obtained from the two platforms.
-
Mandatory Visualizations
The following diagrams, created using the DOT language, illustrate key signaling pathways and experimental workflows relevant to the cross-validation of spectroscopic data.
Caption: A generalized workflow for the cross-validation of spectroscopic data with an orthogonal method.
Caption: A simplified diagram of the EGFR signaling pathway, often studied using mass spectrometry.
Caption: A workflow comparing protein quantification by mass spectrometry and ELISA.
References
- 1. horiba.com [horiba.com]
- 2. Analytical Method Validation in Pharmaceuticals | Step-by-Step Guide to AMV | Pharmaguideline [pharmaguideline.com]
- 3. azom.com [azom.com]
- 4. blog.cellsignal.com [blog.cellsignal.com]
- 5. Validation of UV spectrophotometric and nonaqueous titration methods for the determination of carvedilol in pharmaceutical formulations - PubMed [pubmed.ncbi.nlm.nih.gov]
- 6. Quantitative Raman Chemical Imaging of Intracellular Drug-Membrane Aggregates and Small Molecule Drug Precipitates In Cytoplasmic Organelles - PMC [pmc.ncbi.nlm.nih.gov]
- 7. researchgate.net [researchgate.net]
A Comparative Guide to the Reproducibility of Rotational Constant Measurements
The precise and reproducible determination of rotational constants is fundamental for elucidating molecular structures, understanding intermolecular interactions, and characterizing molecules in various environments, from interstellar space to biological systems. This guide provides a comparative overview of the leading experimental and computational methods for measuring rotational constants, tailored for researchers, scientists, and professionals in drug development.
Data Presentation: Comparison of Methods for Rotational Constant Determination
The reproducibility and accuracy of rotational constant measurements are highly dependent on the chosen methodology. Below is a summary of the typical performance of various techniques.
| Method | Typical Precision/Accuracy | Applicability | Key Advantages | Limitations |
| Microwave Spectroscopy | High (kHz to MHz precision, ~1 part in 10⁶ or better)[1] | Polar molecules in the gas phase[2] | Extremely high resolution and precision; directly measures rotational transitions.[3] | Requires a permanent dipole moment; limited to the gas phase. |
| High-Resolution Infrared Spectroscopy | Good to High (MHz to GHz precision) | Molecules with IR-active vibrational modes | Complements microwave spectroscopy; can study non-polar molecules in vibrationally excited states.[2] | Precision is generally lower than microwave spectroscopy.[2] |
| Raman Spectroscopy | Good to High (MHz to GHz precision) | Molecules with anisotropic polarizability[2] | Ideal for non-polar molecules (e.g., homonuclear diatomics) that are microwave and IR inactive for pure rotation.[2] | Weaker signal than absorption spectroscopy; selection rules differ (ΔJ = ±2).[4][5] |
| Mass-Correlated Rotational Alignment Spectroscopy (mass-CRASY) | Very High (single-kHz accuracy)[6] | Heterogeneous (impure) samples in the gas phase | Isotope-specific measurements; high resolution (3 MHz) and broad bandwidth (500 GHz).[6] | A more specialized and complex experimental setup. |
| Computational Quantum Chemistry | Varies with method (from >1% to <0.1% error) | Broadly applicable to diverse molecules | Cost-effective; provides data for unstable or difficult-to-synthesize molecules; aids in experimental spectral assignment.[7][8] | Accuracy is highly dependent on the level of theory and basis set; requires vibrational corrections for comparison with experimental B₀ values.[9][10][11] |
Experimental and Computational Protocols
Microwave Spectroscopy
Methodology: Microwave spectroscopy measures the absorption of microwave radiation by a gas-phase molecule, which induces transitions between quantized rotational energy levels.[12] For a molecule to be microwave active, it must possess a permanent electric dipole moment.[3]
-
Sample Preparation: The sample is introduced into the spectrometer in the gas phase at low pressure to minimize intermolecular collisions.
-
Instrumentation: A microwave source emits radiation that is passed through the sample cell. The intensity of the transmitted radiation is measured by a detector as the frequency is swept.
-
Data Analysis: The resulting absorption spectrum consists of a series of lines, where the spacing is related to the rotational constant(s) of the molecule.[13] By fitting the observed transition frequencies to a theoretical Hamiltonian (often based on a rigid rotor model with centrifugal distortion corrections), highly precise rotational constants can be extracted.[14]
High-Resolution Infrared Spectroscopy
Methodology: This technique measures the absorption of infrared radiation, which excites vibrational transitions in a molecule. These vibrational bands have a fine structure that arises from simultaneous rotational transitions (ro-vibrational spectra).[15]
-
Sample Preparation: The sample is typically in the gas phase within a long-path absorption cell to enhance weak signals.
-
Instrumentation: A high-resolution Fourier-transform infrared (FTIR) spectrometer is commonly used. An IR source provides broadband radiation, which is passed through the sample and then to an interferometer and detector.
-
Data Analysis: The analysis of the rotational fine structure within a vibrational band allows for the determination of rotational constants for both the ground and vibrationally excited states.[16] The method of combination differences can be employed to extract precise ground state rotational constants.[17] Double resonance techniques, which use both IR and microwave radiation, can significantly enhance the accuracy of the determined rotational constants.[18]
Raman Spectroscopy
Methodology: Raman spectroscopy is a light-scattering technique. When monochromatic light (usually from a laser) interacts with a molecule, most of the light is scattered elastically (Rayleigh scattering). However, a small fraction is scattered inelastically (Raman scattering), with the scattered photons having lost or gained energy corresponding to the molecule's rotational (or vibrational) energy level spacings.[4] For a molecule to have a rotational Raman spectrum, its polarizability must be anisotropic.[2]
-
Sample Preparation: The sample is typically in the gas phase.
-
Instrumentation: A high-power laser is used as the excitation source. The scattered light is collected, passed through a spectrometer to disperse the different frequencies, and detected.
-
Data Analysis: The rotational Raman spectrum consists of lines (Stokes and anti-Stokes) on either side of the strong Rayleigh line. The selection rule for linear molecules is ΔJ = ±2.[5] The spacing of these lines is related to the rotational constant, which can be extracted from the spectrum.
Computational Quantum Chemistry
Methodology: Quantum chemical calculations can predict the equilibrium geometry of a molecule, from which the moments of inertia and subsequently the equilibrium rotational constants (Bₑ) can be derived.[19]
-
Software: A variety of software packages are available, such as Gaussian, ORCA, and Q-Chem.
-
Calculation Steps:
-
Geometry Optimization: The molecular structure is optimized to find the lowest energy conformation at a chosen level of theory (e.g., DFT, MP2, CCSD(T)) and basis set.[10]
-
Rotational Constant Calculation: From the optimized geometry, the principal moments of inertia are calculated, which are then used to determine the rotational constants.[20]
-
Vibrational Correction: The calculated equilibrium rotational constants (Bₑ) do not account for zero-point vibrational effects. To compare with experimental ground-state rotational constants (B₀), a vibrational correction term must be calculated, typically using second-order perturbation theory (VPT2).[21] The accuracy of the final predicted B₀ values is often targeted to be within 0.1% of the experimental values for reliable spectral assignment.[8][22]
-
Visualizations
Workflow for Rotational Constant Determination
The following diagram illustrates the generalized workflow for both experimental and computational approaches to determining rotational constants.
Caption: Workflow for rotational constant determination.
References
- 1. Assessing the performance of rotational spectroscopy in chiral analysis - PMC [pmc.ncbi.nlm.nih.gov]
- 2. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 3. sci.tanta.edu.eg [sci.tanta.edu.eg]
- 4. web.gps.caltech.edu [web.gps.caltech.edu]
- 5. phys.ubbcluj.ro [phys.ubbcluj.ro]
- 6. pnas.org [pnas.org]
- 7. Connections between the accuracy of rotational constants and equilibrium molecular structures - Physical Chemistry Chemical Physics (RSC Publishing) [pubs.rsc.org]
- 8. researchgate.net [researchgate.net]
- 9. pubs.aip.org [pubs.aip.org]
- 10. comporgchem.com [comporgchem.com]
- 11. Scaling of Rotational Constants - PMC [pmc.ncbi.nlm.nih.gov]
- 12. fiveable.me [fiveable.me]
- 13. sci.tanta.edu.eg [sci.tanta.edu.eg]
- 14. physics.dcu.ie [physics.dcu.ie]
- 15. tandfonline.com [tandfonline.com]
- 16. "Analysis of the rotational structure in the high-resolution infrared s" by Norman C. Craig, Yihui Chen et al. [digitalcommons.oberlin.edu]
- 17. chem.libretexts.org [chem.libretexts.org]
- 18. High-resolution ro-vibrational and rotational spectroscopy of HC3O+ - PMC [pmc.ncbi.nlm.nih.gov]
- 19. mailman.cs.uchicago.edu [mailman.cs.uchicago.edu]
- 20. m.youtube.com [m.youtube.com]
- 21. mdpi.com [mdpi.com]
- 22. Connections between the accuracy of rotational constants and equilibrium molecular structures - Physical Chemistry Chemical Physics (RSC Publishing) DOI:10.1039/D2CP04706C [pubs.rsc.org]
A Researcher's Guide to Benchmarking Computational Methods for Predicting Rotational Spectra
For Researchers, Scientists, and Drug Development Professionals
The accurate prediction of rotational spectra is a cornerstone of modern molecular physics and plays a pivotal role in fields ranging from astrochemistry to drug discovery. Computational quantum chemistry provides an indispensable toolkit for predicting these spectra, guiding laboratory experiments, and interpreting complex spectral data. This guide offers an objective comparison of prevalent computational methods, supported by experimental data, to aid researchers in selecting the most appropriate approach for their needs.
The Hierarchy of Computational Methods
The prediction of rotational spectra relies on solving the time-independent Schrödinger equation to determine a molecule's equilibrium geometry and, consequently, its moments of inertia. From these, rotational constants (A, B, C) are derived. The accuracy of these constants is paramount, with a deviation of less than 0.1% from experimental values being the target for predictions to be genuinely useful in guiding high-resolution experiments.[1][2]
Computational methods form a hierarchy based on their accuracy and computational cost. At the pinnacle are high-level ab initio coupled-cluster methods, offering the highest accuracy. Density Functional Theory (DFT) provides a balance of reasonable accuracy and computational efficiency, making it suitable for larger molecules.
Caption: Hierarchy of common quantum chemical methods for rotational spectra prediction.
Performance Benchmarking of Quantum Chemical Methods
The choice of computational method involves a trade-off between accuracy and the size of the molecular system under investigation. The following table summarizes the typical performance of various methods in predicting rotational constants.
Table 1: Comparison of Common Quantum Chemical Methods
| Method | Typical % Error vs. Experiment | Computational Cost | Applicability |
| Coupled-Cluster (CCSD(T)) | < 0.1% - 0.5% [1][3] | Very High | Small to medium-sized molecules (< 20 atoms) |
| Double-Hybrid DFT | ~ 0.3% - 0.5% [2][4] | High | Medium to large molecules |
| Hybrid DFT (e.g., B3LYP, M06-2X) | ~ 0.5% - 2.0% [1][5] | Medium | Large molecules, screening |
| MP2 | ~ 0.4% - 1.0% [1] | Medium-High | Small to medium-sized molecules |
Note: Accuracy is highly dependent on the choice of basis set and the inclusion of vibrational and other corrections.
Coupled-Cluster (CCSD(T)) : Often referred to as the "gold standard" in quantum chemistry, CCSD(T) provides the most accurate predictions but is computationally very demanding.[2] For challenging systems, even CCSD(T) can yield errors greater than 3% if vibrational corrections are not accurately accounted for.[4][6]
Density Functional Theory (DFT) : DFT methods offer a pragmatic alternative for larger systems, such as biomolecule building blocks.[2][7] The accuracy of DFT is highly dependent on the chosen functional. Double-hybrid functionals, like rev-DSD-PBEP86, can approach the accuracy of composite coupled-cluster schemes at a fraction of the computational cost.[2] Standard hybrid functionals such as B3LYP or ωB97X-D are workhorses for routine calculations, but their accuracy can be variable.[5] The inclusion of dispersion corrections (e.g., -D3) is often crucial for obtaining reliable geometries and, consequently, accurate rotational constants.[5]
Table 2: Performance of Selected DFT Functionals for Rotational Constants (Mean Absolute Error)
| Functional | Basis Set | Mean Absolute Error (%) | Reference |
| DSD-PBEP86-D3BJ | Varies | < 0.5% | [4][6] |
| rev-DSD-PBEP86 | jun-cc-pVTZ | ~0.3% | [2] |
| ChS (MP2-based composite) | cc-pVTZ | 0.13% | [1] |
| MP2 | cc-pVTZ | 0.43% | [1] |
| CCSD(T) | cc-pVTZ | 0.80% | [1] |
Experimental and Computational Protocols
Achieving high accuracy in predicted rotational spectra requires a multi-step computational workflow. The process goes beyond simple geometry optimization and involves crucial correction factors.
Standard Computational Workflow
The prediction of a rotational spectrum from first principles is a systematic process:
-
Geometry Optimization : The starting point is to find the minimum energy structure of the molecule. This is performed using a chosen level of theory (e.g., CCSD(T) or a reliable DFT functional) and a suitable basis set (e.g., triple-zeta quality like cc-pVTZ or larger).[1][3]
-
Equilibrium Rotational Constants (Be) : From the optimized geometry, the principal moments of inertia are calculated, which directly yield the equilibrium rotational constants (Ae, Be, Ce). These constants represent over 99% of the final value.[2]
-
Vibrational Corrections : Molecules are not static; they vibrate even in their ground state. This zero-point vibrational motion affects the observed rotational constants. Second-order vibrational perturbation theory (VPT2) is the most common method to compute these corrections, transforming Be to the experimentally relevant ground-state constants (B0).[2][8] This step is computationally intensive as it requires calculating the anharmonic force field (cubic and semi-diagonal quartic force constants).[2][9] The vibrational contribution is typically 0.1% to 0.7% of the equilibrium constant's magnitude.[1][2]
-
Spectrum Simulation : The final B0 constants, along with calculated centrifugal distortion constants and electric dipole moments, are used as input for specialized spectral simulation software like PGOPHER or SPCAT .[10] These programs generate a theoretical spectrum that can be directly compared with experimental results.
Caption: A standard computational workflow for predicting rotational spectra.
Key Software Packages
A variety of software packages are available to perform these calculations. Many are commercial, while others are open-source.
-
Quantum Chemistry Suites :
-
Gaussian : A widely used commercial package for a broad range of quantum chemical calculations.[2]
-
CFOUR : A program package focused on high-accuracy coupled-cluster methods.[2]
-
MOLPRO : A comprehensive system of ab initio programs with a focus on high-level methods.[2]
-
Q-Chem : A versatile commercial package for predicting molecular properties.[11]
-
ORCA : A flexible and efficient quantum chemistry program.
-
-
Spectrum Simulation :
-
PGOPHER : A general-purpose, open-source program for simulating and fitting rotational, vibrational, and electronic spectra.[10]
-
SPCAT/SPFIT : A suite of programs widely used in the analysis of rotational spectra, particularly in astrophysics.
-
References
- 1. Connections between the accuracy of rotational constants and equilibrium molecular structures - Physical Chemistry Chemical Physics (RSC Publishing) DOI:10.1039/D2CP04706C [pubs.rsc.org]
- 2. mdpi.com [mdpi.com]
- 3. rune.une.edu.au [rune.une.edu.au]
- 4. researchgate.net [researchgate.net]
- 5. Benchmarking quantum chemical methods for accurate gas-phase structure predictions of carbonyl compounds: the case of ethyl butyrate - Physical Chemistry Chemical Physics (RSC Publishing) DOI:10.1039/D2CP05774C [pubs.rsc.org]
- 6. mdpi.com [mdpi.com]
- 7. Toward Accurate yet Effective Computations of Rotational Spectroscopy Parameters for Biomolecule Building Blocks - PubMed [pubmed.ncbi.nlm.nih.gov]
- 8. Generalized Vibrational Perturbation Theory for Rotovibrational Energies of Linear, Symmetric and Asymmetric Tops: Theory, Approximations, and Automated Approaches to Deal with Medium-to-Large Molecular Systems - PMC [pmc.ncbi.nlm.nih.gov]
- 9. 5.19. Anharmonic Analysis and Vibrational Corrections using VPT2/GVPT2 and orca_vpt2 — ORCA 6.1.1 Manual [orca-manual.mpi-muelheim.mpg.de]
- 10. researchgate.net [researchgate.net]
- 11. iscitech.com [iscitech.com]
Unveiling Molecular Structure: A Comparative Guide to Rotational Spectra of Isotopically Substituted Molecules
For researchers, scientists, and drug development professionals, understanding the subtle nuances of molecular structure is paramount. Rotational spectroscopy, a high-resolution technique, provides a powerful tool to probe the three-dimensional arrangement of atoms within a molecule. The substitution of an atom with one of its isotopes induces small but measurable changes in the rotational spectrum, offering a precise method for structural determination and validation.
This guide provides an objective comparison of the rotational spectra of molecules upon isotopic substitution, supported by experimental data. We will delve into the theoretical underpinnings, present quantitative data in a clear, tabular format, and provide detailed experimental methodologies.
The Principle of Isotopic Substitution in Rotational Spectroscopy
The rotational energy levels of a molecule are quantized and depend on its moments of inertia.[1][2] The moment of inertia, in turn, is a function of the masses of the constituent atoms and their distances from the center of mass of the molecule.[1] When an atom in a molecule is replaced by one of its isotopes, the atomic mass changes, leading to a change in the molecule's moment of inertia.[3][4][5] This alteration in the moment of inertia directly affects the rotational energy levels and, consequently, the frequencies of transitions observed in the rotational spectrum.[1][6]
Crucially, isotopic substitution does not significantly alter the internuclear distances (bond lengths) or the molecular geometry, as the chemical bonding is primarily determined by the electronic structure, which is the same for isotopes of an element.[3][4][5] This principle allows for the precise determination of atomic positions and bond lengths. By analyzing the rotational spectra of different isotopologues (molecules that differ only in their isotopic composition), a complete and accurate molecular structure can be determined.[7][8]
A heavier isotope leads to a larger moment of inertia, which results in a smaller rotational constant (B) and consequently, a smaller spacing between the rotational spectral lines.[3][4][5][6] This relationship is fundamental to the analysis of rotational spectra of isotopically substituted molecules.
Comparative Data of Isotopically Substituted Molecules
The following table summarizes the rotational constants (B) and bond lengths (r) for various isotopologues of diatomic and polyatomic molecules, showcasing the effect of isotopic substitution.
| Molecule | Isotopologue | Rotational Constant (B) (cm⁻¹) | Bond Length (Å) | Reference |
| Carbon Monoxide | ¹²C¹⁶O | 1.92118 | 1.128 | [3][5] |
| ¹³C¹⁶O | 1.83669 | 1.128 | [3][5] | |
| Hydrogen Chloride | H³⁵Cl | 10.59341 | 1.2745 | |
| H³⁷Cl | 10.57799 | 1.2745 | ||
| D³⁵Cl | 5.44879 | 1.2745 | ||
| D³⁷Cl | 5.43938 | 1.2745 | ||
| Acetone | (CH₃)₂CO | A=10137.3, B=8909.1, C=5159.4 (MHz) | C=O: 1.212, C-C: 1.517, C-H: 1.091 | [9][10] |
| (¹³CH₃)₂CO | A=9814.9, B=8688.2, C=5061.5 (MHz) | C=O: 1.212, C-C: 1.517, C-H: 1.091 | [9][10] | |
| (CH₃)₂C¹⁸O | A=10137.1, B=8405.3, C=4967.9 (MHz) | C=O: 1.212, C-C: 1.517, C-H: 1.091 | [9][10] |
Note: The bond lengths are generally assumed to be constant upon isotopic substitution, a cornerstone of this analytical technique. The rotational constants for polyatomic molecules (like Acetone) are given for the three principal axes of rotation (A, B, C).
Experimental Protocol: Rotational Spectroscopy
The acquisition of rotational spectra is typically performed using microwave or millimeter-wave spectroscopy in the gas phase.[2][7]
A generalized experimental workflow is as follows:
-
Sample Preparation: The molecule of interest is introduced into the gas phase at low pressure (typically a few mTorr) within a sample cell.[7] For non-volatile samples, heating or laser ablation techniques may be employed.
-
Radiation Source: A tunable source of microwave or millimeter-wave radiation is used to irradiate the gaseous sample.
-
Interaction and Detection: As the frequency of the radiation is swept, the molecules will absorb energy at specific frequencies corresponding to the transitions between their rotational energy levels. A detector measures the absorption of radiation as a function of frequency.
-
Data Analysis: The resulting spectrum, a plot of absorption intensity versus frequency, is analyzed to identify the transition frequencies. These frequencies are then used to determine the rotational constants of the molecule.[2]
-
Isotopic Substitution: To determine the molecular structure, the process is repeated for different isotopically labeled versions of the molecule.[8][11] The analysis of the rotational constants from multiple isotopologues allows for the precise calculation of bond lengths and angles.[12][13]
Caption: Experimental workflow for rotational spectroscopy.
The Logic of Isotopic Substitution Analysis
The power of using isotopic substitution lies in the systematic way it alters the rotational spectrum, providing the necessary data to solve for the geometric parameters of the molecule. The logical relationship between isotopic substitution and the resulting spectral changes is outlined below.
Caption: Logical flow of isotopic substitution analysis.
Conclusion
The comparison of rotational spectra of isotopically substituted molecules is a cornerstone of modern structural chemistry. This guide has highlighted the fundamental principles, provided comparative data, and outlined the experimental and logical frameworks of this powerful technique. For researchers in drug development and other scientific fields, the precise structural information gleaned from this method is invaluable for understanding molecular interactions and designing novel therapeutic agents.
References
- 1. Effect of isotopic substution on rotational spectra | Filo [askfilo.com]
- 2. Rotational spectroscopy - Wikipedia [en.wikipedia.org]
- 3. dumkalcollege.in [dumkalcollege.in]
- 4. goalparacollege.ac.in [goalparacollege.ac.in]
- 5. dpbspgcollege.edu.in [dpbspgcollege.edu.in]
- 6. m.youtube.com [m.youtube.com]
- 7. undergradresearch.chem.wisc.edu [undergradresearch.chem.wisc.edu]
- 8. pubs.aip.org [pubs.aip.org]
- 9. pubs.acs.org [pubs.acs.org]
- 10. researchgate.net [researchgate.net]
- 11. pubs.aip.org [pubs.aip.org]
- 12. pubs.aip.org [pubs.aip.org]
- 13. Rotational spectroscopy of isotopic cyclopropenone, c-H2C3O, and determination of its equilibrium structure | Astronomy & Astrophysics (A&A) [aanda.org]
A Comparative Guide: Unveiling the Advantages of Microwave Spectroscopy over Raman for Rotational Studies
For researchers, scientists, and drug development professionals engaged in the precise characterization of molecular structures, understanding the nuances of spectroscopic techniques is paramount. This guide provides a detailed comparison of microwave and Raman spectroscopy for rotational studies, highlighting the distinct advantages of microwave spectroscopy in achieving unparalleled resolution and sensitivity. The information presented is supported by experimental data and detailed methodologies to aid in informed decision-making for your research endeavors.
Executive Summary
Microwave spectroscopy and Raman spectroscopy are powerful tools for probing the rotational energy levels of molecules, providing insights into molecular geometry, bond lengths, and angles. While both techniques yield valuable information, microwave spectroscopy offers significant advantages in terms of resolution, precision, and sensitivity for molecules with a permanent dipole moment. This guide will delve into the fundamental principles of each technique, present a quantitative comparison of their performance, detail the experimental protocols, and provide a visual representation of the underlying concepts and workflows.
Fundamental Principles: A Tale of Two Interactions
The key distinction between microwave and Raman spectroscopy lies in their fundamental interaction with molecules.
Microwave Spectroscopy operates on the principle of direct absorption . Molecules possessing a permanent electric dipole moment can directly absorb microwave radiation, causing transitions between quantized rotational energy levels.[1] This absorption is highly specific and results in a spectrum with exceptionally sharp lines, directly corresponding to the energy differences between rotational states.
Raman Spectroscopy , conversely, is a scattering technique.[2] When a high-intensity monochromatic laser beam interacts with a molecule, most of the light is scattered elastically (Rayleigh scattering) at the same frequency. However, a small fraction of the light is scattered inelastically (Raman scattering), with a frequency that is shifted up or down. This frequency shift corresponds to the energy of the molecule's rotational (and vibrational) transitions. For a rotational Raman spectrum to be observed, the molecule's polarizability must change as it rotates.[2]
Quantitative Comparison: Resolution and Precision
The most significant advantage of microwave spectroscopy for rotational studies is its inherently higher resolution and precision. This is evident when comparing the experimentally determined rotational constants for various molecules.
| Parameter | Microwave Spectroscopy | Raman Spectroscopy |
| Typical Resolution | 0.0001 cm⁻¹ (3 MHz) | 0.1 - 1 cm⁻¹ |
| Rotational Constant (B₀) for ¹⁶O¹²C³²S | 6081.4913 MHz (0.202855 cm⁻¹)[3][4] | Not readily found with comparable precision |
| Rotational Constant (B₀) for ¹⁴N₂ | Not applicable (no permanent dipole) | 1.98973 ± 0.0003 cm⁻¹[5] |
| Rotational Constant (B₀) for ¹²C¹⁶O | 57635.968 MHz (1.922529 cm⁻¹)[6][7][8] | Not the preferred method for this level of precision |
As the table demonstrates, microwave spectroscopy can determine rotational constants with sub-MHz precision, leading to highly accurate calculations of bond lengths and angles. While Raman spectroscopy is indispensable for studying non-polar molecules like nitrogen (N₂), its resolution is generally lower than that of microwave spectroscopy.[5][9]
Experimental Protocols
High-Resolution Fourier Transform Microwave (FTMW) Spectroscopy
Objective: To obtain the pure rotational spectrum of a gas-phase molecule with a permanent dipole moment.
Methodology:
-
Sample Introduction: The gaseous sample is introduced into a high-vacuum chamber via a pulsed nozzle. This creates a supersonic jet, which cools the molecules to a very low rotational temperature (a few Kelvin), simplifying the spectrum by populating only the lowest rotational levels.
-
Microwave Excitation: A short, high-power microwave pulse is directed into the vacuum chamber, interacting with the molecular jet. If the microwave frequency is resonant with a rotational transition, the molecules are coherently excited.
-
Free Induction Decay (FID) Detection: After the microwave pulse, the coherently rotating molecules emit a faint microwave signal, known as the Free Induction Decay (FID). This signal is detected by a sensitive receiver.
-
Fourier Transformation: The time-domain FID signal is digitized and then mathematically transformed into the frequency domain using a Fourier transform. This results in a high-resolution frequency spectrum, where the peaks correspond to the rotational transitions.
-
Data Analysis: The frequencies of the rotational transitions are precisely measured from the spectrum. These frequencies are then used to determine the rotational constants and other molecular parameters.
High-Resolution Raman Spectroscopy of Gases
Objective: To obtain the pure rotational Raman spectrum of a gas-phase molecule.
Methodology:
-
Sample Containment: The gaseous sample is contained in a specialized gas cell, often with multi-pass mirrors to increase the interaction length of the laser beam with the sample.
-
Laser Excitation: A high-intensity, monochromatic laser beam (e.g., from an Argon ion laser) is passed through the gas cell.
-
Scattered Light Collection: The light scattered by the gas molecules at a 90° angle to the incident laser beam is collected by a lens system.
-
Rayleigh Filtering: A series of filters or a multi-stage spectrometer is used to reject the intense Rayleigh scattered light, which is at the same frequency as the laser.
-
Dispersion and Detection: The remaining weakly scattered Raman light is dispersed by a high-resolution grating spectrometer and detected by a sensitive detector, such as a photomultiplier tube or a CCD camera.
-
Data Analysis: The Raman spectrum shows a series of lines (Stokes and anti-Stokes) shifted from the laser frequency. The frequency shifts of these lines are measured to determine the rotational energy level spacings and, consequently, the rotational constants.
Visualizing the Processes
To better understand the workflows and fundamental differences, the following diagrams are provided.
Advantages of Microwave Spectroscopy for Rotational Studies
The primary advantages of microwave spectroscopy over Raman spectroscopy for the study of rotational transitions in polar molecules can be summarized as follows:
-
Higher Resolution and Precision: As demonstrated by the experimental data, microwave spectroscopy offers significantly higher resolution, allowing for more precise determination of rotational constants and molecular structures.
-
Greater Sensitivity: For molecules with even a small permanent dipole moment, microwave spectroscopy is generally more sensitive than Raman spectroscopy. Raman scattering is an inherently weak phenomenon, often requiring powerful lasers and sensitive detection systems.[2]
-
Direct Measurement: Microwave spectroscopy involves the direct absorption of radiation, leading to a more straightforward interpretation of the resulting spectra.
-
Simplified Spectra at Low Temperatures: The use of supersonic jets in FTMW spectroscopy leads to significant cooling of the molecules, resulting in much simpler spectra with fewer populated rotational states. This greatly aids in the assignment and analysis of the spectral lines.
When to Choose Raman Spectroscopy
Despite the advantages of microwave spectroscopy, Raman spectroscopy remains an essential tool for rotational studies in specific scenarios:
-
Non-Polar Molecules: Raman spectroscopy is the only technique of the two that can be used to study the rotational spectra of non-polar molecules, such as homonuclear diatomics (e.g., N₂, O₂, H₂) and spherical tops (e.g., CH₄), which are microwave inactive.[10][11]
-
Complementary Information: The different selection rules for the two techniques (ΔJ = ±1 for microwave vs. ΔJ = 0, ±2 for Raman) can provide complementary information about a molecule's rotational energy levels.[10]
Conclusion
For researchers aiming to determine the precise rotational constants and geometric structures of polar molecules, microwave spectroscopy, particularly Fourier Transform Microwave (FTMW) spectroscopy, stands as the superior technique due to its exceptional resolution, precision, and sensitivity. While Raman spectroscopy is a vital and complementary tool, especially for the study of non-polar molecules, the level of detail and accuracy achievable with microwave spectroscopy for suitable candidates is unparalleled. The choice of technique will ultimately depend on the specific properties of the molecule under investigation and the research questions being addressed. This guide provides the foundational knowledge and data to make an informed decision, ensuring the selection of the most appropriate and powerful tool for your molecular structure elucidation needs.
References
- 1. chem.libretexts.org [chem.libretexts.org]
- 2. Rotational and Vibrational Raman spectra – Atomic, Molecular and Laser Spectroscopy [ebooks.inflibnet.ac.in]
- 3. srd.nist.gov [srd.nist.gov]
- 4. files01.core.ac.uk [files01.core.ac.uk]
- 5. cdnsciencepub.com [cdnsciencepub.com]
- 6. phys.chem.elte.hu [phys.chem.elte.hu]
- 7. mdpi.com [mdpi.com]
- 8. Untitled Document [andrew.cmu.edu]
- 9. Pure rotational Raman spectroscopy applied to N2/O2 analysis of air bubbles in polar firn | Journal of Glaciology | Cambridge Core [cambridge.org]
- 10. m.youtube.com [m.youtube.com]
- 11. srd.nist.gov [srd.nist.gov]
A Researcher's Guide to Validating Spectral Assignments with Double Resonance NMR Techniques
In the intricate world of molecular characterization, the unambiguous assignment of nuclear magnetic resonance (NMR) signals to specific atoms within a molecule is a critical and often challenging task. Double resonance NMR techniques have emerged as indispensable tools for researchers, providing powerful methods to unravel complex spectra and confidently validate spectral assignments. This guide offers an objective comparison of the most common double resonance techniques, complete with experimental data, detailed protocols, and visual workflows to aid researchers, scientists, and drug development professionals in their quest for accurate molecular structure elucidation.
Unraveling Complexity: An Introduction to Double Resonance
Double resonance, in the context of NMR spectroscopy, involves the simultaneous application of two distinct radiofrequency (RF) fields. One RF field is used to observe the NMR signal of a specific nucleus (the "observe" channel), while the second RF field is used to irradiate another nucleus (the "decoupling" or "perturbation" channel). This perturbation of the second nucleus induces changes in the observed spectrum, revealing valuable information about through-bond (scalar) or through-space (dipolar) interactions. These interactions form the basis for correlating different nuclei and, consequently, for validating their assignments.
The most widely employed double resonance experiments are two-dimensional (2D) NMR techniques, where the data is presented as a contour plot with two frequency axes. These experiments provide a visual map of correlations between nuclei, simplifying the interpretation of often-crowded 1D spectra.
At a Glance: Comparing Key Double Resonance Techniques
The choice of a specific double resonance technique depends on the information sought and the nature of the molecule under investigation. The four most common and powerful 2D NMR experiments for spectral assignment validation are COSY, HSQC, HMBC, and NOESY. The following table provides a quantitative comparison of these techniques.
| Technique | Correlation Type & Nuclei | Information Provided | Typical Experiment Time (High-Resolution) | Relative Sensitivity | Typical Resolution |
| COSY (Correlation Spectroscopy) | Homonuclear (¹H-¹H) | Through-bond scalar coupling (typically 2-3 bonds) | 0.5 - 2 hours | High | High in both dimensions |
| HSQC (Heteronuclear Single Quantum Coherence) | Heteronuclear (¹H-¹³C or ¹H-¹⁵N) | Direct one-bond scalar coupling | 1 - 4 hours | Moderate | High in ¹H, Moderate in X-nucleus |
| HMBC (Heteronuclear Multiple Bond Correlation) | Heteronuclear (¹H-¹³C or ¹H-¹⁵N) | Long-range scalar coupling (typically 2-4 bonds) | 2 - 8 hours | Low | High in ¹H, Moderate in X-nucleus |
| NOESY (Nuclear Overhauser Effect Spectroscopy) | Homonuclear (¹H-¹H) | Through-space dipolar coupling (typically < 5 Å) | 4 - 12 hours | Moderate to Low | High in both dimensions |
In Detail: A Deeper Dive into the Techniques
COSY: Mapping Proton-Proton Connections
Correlation Spectroscopy (COSY) is the cornerstone of homonuclear correlation experiments. It identifies protons that are scalar-coupled to each other, typically over two or three bonds. A cross-peak at the intersection of the chemical shifts of two protons in a COSY spectrum indicates that these two protons are coupled. This is invaluable for identifying adjacent protons in a spin system, such as those on neighboring carbon atoms in an aliphatic chain or an aromatic ring.
HSQC: Linking Protons to their Directly Attached Heteroatoms
The Heteronuclear Single Quantum Coherence (HSQC) experiment is a highly sensitive method for correlating protons with their directly attached heteroatoms, most commonly ¹³C or ¹⁵N. Each peak in an HSQC spectrum corresponds to a specific ¹H nucleus and the heteroatom it is directly bonded to. This experiment is fundamental for assigning the chemical shifts of carbon or nitrogen atoms based on the already assigned proton shifts.
HMBC: Unveiling Long-Range Connections
The Heteronuclear Multiple Bond Correlation (HMBC) experiment provides information about longer-range scalar couplings, typically over two to four bonds. This is particularly useful for identifying connections between protons and quaternary carbons (carbons with no attached protons) or for linking different spin systems together across heteroatoms. HMBC is a powerful tool for assembling the complete carbon skeleton of a molecule.
NOESY: Probing Spatial Proximity
Unlike the previous techniques that rely on through-bond couplings, the Nuclear Overhauser Effect Spectroscopy (NOESY) experiment detects through-space dipolar interactions between protons that are close to each other in space (typically less than 5 Å), regardless of whether they are connected through bonds. This is crucial for determining the three-dimensional structure and stereochemistry of a molecule.
From Sample to Spectrum: Experimental Protocols
The success of any double resonance experiment hinges on meticulous sample preparation and the appropriate selection of experimental parameters.
Sample Preparation
For optimal results, particularly for biomolecules like proteins, the following sample conditions are recommended:
-
Concentration: For proteins, a concentration of 0.1 - 2.5 mM is typical, with around 1 mM being a common target.[1] For small molecules, higher concentrations are often used.
-
Volume: A sample volume of 500-550 µL is standard for 5 mm NMR tubes.[1]
-
Purity: The sample should be highly pure (>95%) and free from paramagnetic impurities.[1]
-
Buffer and pH: A suitable buffer system should be used to maintain a stable pH, typically neutral or slightly acidic for proteins.[1] Phosphate buffers are often preferred.[1]
-
Isotopic Labeling: For proteins larger than ~10 kDa, uniform ¹³C and/or ¹⁵N labeling is often necessary to resolve spectral overlap and enable heteronuclear correlation experiments.[2][3]
Key Experimental Parameters
The following table outlines some of the key acquisition parameters for each technique. The specific values will need to be optimized for the molecule of interest and the spectrometer being used.
| Parameter | COSY | HSQC | HMBC | NOESY |
| Pulse Program | cosygpqf (or similar) | hsqcetgpsi (or similar) | hmbcgplpndqf (or similar) | noesygpph (or similar) |
| Number of Scans (ns) | 2-16 | 4-32 | 8-64 | 16-128 |
| Number of Increments (t1) | 256-512 | 128-256 | 256-512 | 256-512 |
| Spectral Width (sw) | Optimized based on ¹H spectrum | Optimized for ¹H and X-nucleus | Optimized for ¹H and X-nucleus | Optimized based on ¹H spectrum |
| Relaxation Delay (d1) | 1-2 s | 1-2 s | 1-2 s | 1-2 s |
| Mixing Time (d8/d9) | N/A | N/A | N/A | 100-400 ms |
Visualizing the Workflow: From Data to Assignment
The process of validating spectral assignments using double resonance techniques follows a logical workflow. The following diagrams, generated using the DOT language, illustrate this process.
Data Processing and Interpretation: A Step-by-Step Approach
The raw data from 2D NMR experiments (the Free Induction Decay, or FID) must be processed to generate the final spectrum. This typically involves the following steps:
-
Fourier Transformation: The time-domain data (FID) is converted into the frequency domain. This is performed for both dimensions of the 2D data.
-
Phasing: The phase of the spectrum is corrected to ensure that all peaks have the correct absorptive shape.
-
Baseline Correction: The baseline of the spectrum is flattened to remove distortions.
-
Referencing: The chemical shift axes are referenced to a known standard, such as tetramethylsilane (B1202638) (TMS) or the solvent signal.
-
Peak Picking: The coordinates of the cross-peaks are identified.
Once the spectra are processed, the interpretation and assignment process can begin, following the logical workflow depicted in Diagram 2. This iterative process of correlating information from different experiments allows for the confident and unambiguous assignment of all NMR signals.
Conclusion
Double resonance NMR techniques are indispensable for the accurate and reliable validation of spectral assignments. By providing a rich tapestry of through-bond and through-space correlations, experiments like COSY, HSQC, HMBC, and NOESY empower researchers to decipher complex molecular structures with a high degree of confidence. The systematic application of these techniques, guided by robust experimental protocols and a logical interpretation workflow, is fundamental to advancing our understanding of molecular structure and function in chemistry, biology, and medicine.
References
Safety Operating Guide
Navigating the Safe Disposal of Topps Products in a Laboratory Setting
Proper disposal of chemical products is a critical component of laboratory safety and environmental responsibility. For researchers, scientists, and drug development professionals utilizing Topps products, understanding the correct disposal procedures is essential to maintain a safe work environment and comply with regulatory standards. This guide provides a comprehensive overview of the necessary steps and precautions for the proper disposal of this compound materials, ensuring the protection of personnel and the environment.
Key Disposal and Safety Information Summary
The following table summarizes crucial information derived from the Material Safety Data Sheets (MSDS) for this compound products, offering a quick reference for safe handling and disposal.
| Information Category | Key Guidance | Source |
| Personal Protective Equipment (PPE) | Safety glasses with side shields, rubber gloves, and appropriate respiratory protection (NIOSH approved mask if needed) are recommended. Contaminated clothing should be changed immediately. | [1] |
| Spill and Leak Cleanup | Absorb spills with inert materials like sand or sawdust. Contaminated absorbent material should be discarded in accordance with local and state regulations. Wash contaminated surfaces and equipment before the material dries. | [1] |
| Container Disposal | Dispose of contents and containers at an approved waste disposal plant.[2] Empty containers should not be exposed to heat, sparks, or open flames and must be disposed of according to federal, state, and local regulations.[2] | |
| First Aid: Eyes | Immediately flush eyes with cool, clean, low-pressure water for at least 15 minutes, occasionally lifting the eyelids. Remove contact lenses if present and easy to do. Seek medical attention if irritation persists. | [1][2] |
| First Aid: Skin | Remove contaminated clothing. Wash the affected area with soap and water. Seek medical attention if irritation or pain persists. | [1] |
| First Aid: Ingestion | If conscious, give several glasses of water but do not induce vomiting. Seek immediate medical attention. | [2] |
| First Aid: Inhalation | Move the victim to fresh air. If not breathing, begin rescue breathing. Seek medical attention. | [1] |
| Storage | Store in a cool, dry, well-ventilated area in tightly closed containers. Keep away from heat, flames, and strong oxidizing agents. | [1][2] |
Procedural Guidance for Disposal
The proper disposal of this compound products, as with any laboratory chemical, should be approached systematically to ensure safety and compliance. The following steps provide a general protocol for laboratory personnel.
Step 1: Waste Identification and Segregation
-
Characterize the Waste: Determine if the waste is hazardous. Based on the MSDS, this compound products may have characteristics that classify them as hazardous waste.
-
Segregate Waste Streams: Do not mix different types of waste. Keep this compound product waste separate from other chemical, biological, or radioactive waste streams unless explicitly instructed by your institution's Environmental Health and Safety (EHS) office. Incompatible materials must be kept separate to avoid dangerous reactions.[3][4]
Step 2: Container Selection and Labeling
-
Use Appropriate Containers: Waste must be stored in containers that are compatible with the chemical properties of the this compound product to prevent leaks or reactions.[3] Containers should be in good condition with secure, tight-fitting lids.
-
Properly Label Containers: All waste containers must be clearly labeled with the words "Hazardous Waste," the full chemical name of the contents (no abbreviations), and the date accumulation started.[4]
Step 3: Accumulation and Storage
-
Designated Satellite Accumulation Area (SAA): Hazardous waste must be stored in a designated SAA within the laboratory where it is generated.[3]
-
Storage Conditions: The SAA should be in a cool, dry, and well-ventilated area, away from sources of ignition.[2] Ensure secondary containment is used to capture any potential leaks.
Step 4: Disposal
-
Follow Institutional Procedures: Adhere to your institution's specific procedures for hazardous waste pickup and disposal. Contact your EHS office for guidance.
-
Approved Waste Disposal: As stated in the MSDS, this compound product waste must be disposed of through an approved waste disposal plant.[2] Do not dispose of this material down the drain or in the regular trash.[5]
Logical Workflow for Laboratory Waste Disposal
The following diagram illustrates the decision-making process for the proper disposal of laboratory waste, including products like this compound.
Caption: Laboratory Waste Disposal Workflow.
By adhering to these procedures and utilizing the provided safety information, laboratory professionals can ensure the safe and compliant disposal of this compound products, fostering a secure and responsible research environment. Always consult your institution's specific guidelines and the product's Safety Data Sheet for the most accurate and detailed information.
References
- 1. toppsproductssa.co.za [toppsproductssa.co.za]
- 2. toppsproducts.com [toppsproducts.com]
- 3. Central Washington University | Laboratory Hazardous Waste Disposal Guidelines [cwu.edu]
- 4. nems.nih.gov [nems.nih.gov]
- 5. Guide to Laboratory Sink/Sewer Disposal of Wastes | Office of Clinical and Research Safety [vumc.org]
Essential Safety and Handling Guide for TAPS Buffer
This guide provides crucial safety and logistical information for researchers, scientists, and drug development professionals handling N-[Tris(hydroxymethyl)methyl]-3-aminopropanesulfonic acid), commonly known as TAPS buffer. Adherence to these procedures is critical for ensuring personnel safety, environmental protection, and regulatory compliance. While TAPS buffer is not classified as a hazardous substance or mixture according to Regulation (EC) No. 1272/2008, good laboratory practices should always be followed.[1][2]
Personal Protective Equipment (PPE)
Appropriate personal protective equipment must be worn when handling TAPS buffer to minimize exposure and ensure safety.
| PPE Category | Specification | Rationale |
| Eye/Face Protection | Safety glasses with side shields or chemical splash goggles. | Protects eyes from potential splashes of the buffer solution.[1][3][4] |
| Skin Protection | Chemical-resistant gloves (e.g., nitrile) and a lab coat. | Prevents skin contact with the buffer. Gloves should be inspected before use and removed properly to avoid contamination.[1][3][4] |
| Respiratory Protection | Not typically required for normal use. A NIOSH-approved respirator should be used if dust formation is likely.[1][3] | Avoids inhalation of any potential vapors or aerosols. |
Operational Plan: Step-by-Step Handling Protocol
Follow these steps for the safe handling of TAPS buffer in a laboratory setting.
-
Preparation :
-
Weighing and Solution Preparation :
-
If working with powdered TAPS, handle it in a way that minimizes dust generation.[1]
-
Measure the desired amount of TAPS buffer.
-
Dissolve the buffer in the appropriate solvent, typically purified water.
-
-
Use in Experiments :
-
Storage :
Accidental Release and First Aid Measures
| Situation | Procedure |
| Spill | For small spills, sweep up the solid material, avoiding dust formation, and place it in a suitable, closed container for disposal.[1][3] Ventilate the area and wash the spill site after material pickup is complete.[3] Do not let the product enter drains.[1] |
| Skin Contact | Wash the affected area with soap and plenty of water.[1][5] |
| Eye Contact | Immediately flush the eyes with plenty of water for at least 15 minutes as a precaution.[1][3][5] |
| Inhalation | If inhaled, move the person to fresh air. If breathing is difficult, give oxygen.[1][3] |
| Ingestion | Rinse the mouth with water. Never give anything by mouth to an unconscious person.[1][5] |
Disposal Plan
Proper disposal of TAPS buffer and contaminated materials is essential to prevent environmental contamination and ensure regulatory compliance.
-
Unused Product : Offer surplus and non-recyclable solutions to a licensed disposal company.[1] Dispose of the unused product in the same manner as the original product.[1]
-
Contaminated Materials : Items such as gloves, pipette tips, and weigh boats that have come into contact with TAPS buffer should be disposed of as unused product.[1]
-
Drain Disposal : According to the NIH Drain Discharge Guide, TAPS buffer is approved for drain disposal.[6] However, always consult and adhere to your institution's specific waste disposal guidelines.[7][8]
Experimental Workflow and Safety Protocols Diagram
References
- 1. cdhfinechemical.com [cdhfinechemical.com]
- 2. suvchemlaboratorychemicals.com [suvchemlaboratorychemicals.com]
- 3. gentaur-search.com [gentaur-search.com]
- 4. benchchem.com [benchchem.com]
- 5. lobachemie.com [lobachemie.com]
- 6. nems.nih.gov [nems.nih.gov]
- 7. Hazardous Waste Disposal Guide - Research Areas | Policies [policies.dartmouth.edu]
- 8. ehs.umich.edu [ehs.umich.edu]
Featured Recommendations
| Most viewed | ||
|---|---|---|
| Most popular with customers |
Disclaimer and Information on In-Vitro Research Products
Please be aware that all articles and product information presented on BenchChem are intended solely for informational purposes. The products available for purchase on BenchChem are specifically designed for in-vitro studies, which are conducted outside of living organisms. In-vitro studies, derived from the Latin term "in glass," involve experiments performed in controlled laboratory settings using cells or tissues. It is important to note that these products are not categorized as medicines or drugs, and they have not received approval from the FDA for the prevention, treatment, or cure of any medical condition, ailment, or disease. We must emphasize that any form of bodily introduction of these products into humans or animals is strictly prohibited by law. It is essential to adhere to these guidelines to ensure compliance with legal and ethical standards in research and experimentation.


