molecular formula C20H23ClN2O3S B1670996 DVR-01

DVR-01

Cat. No.: B1670996
M. Wt: 406.9 g/mol
InChI Key: PBAWFYZFSXYUOS-UHFFFAOYSA-N
Attention: For research use only. Not for human or veterinary use.
Usually In Stock
  • Click on QUICK INQUIRY to receive a quote from our team of experts.
  • With the quality product at a COMPETITIVE price, you can focus more on your research.

Description

DVR-01 is a potent HBV capsid inhibitor.

Properties

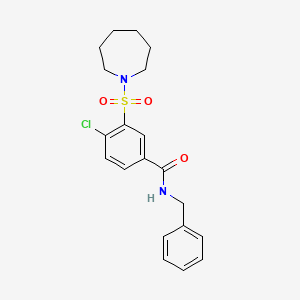
Molecular Formula

 C20H23ClN2O3S

Molecular Weight

 406.9 g/mol

IUPAC Name

 3-(azepan-1-ylsulfonyl)-N-benzyl-4-chlorobenzamide

InChI

 InChI=1S/C20H23ClN2O3S/c21-18-11-10-17(20(24)22-15-16-8-4-3-5-9-16)14-19(18)27(25,26)23-12-6-1-2-7-13-23/h3-5,8-11,14H,1-2,6-7,12-13,15H2,(H,22,24)

InChI Key

 PBAWFYZFSXYUOS-UHFFFAOYSA-N

Canonical SMILES

 C1CCCN(CC1)S(=O)(=O)C2=C(C=CC(=C2)C(=O)NCC3=CC=CC=C3)Cl

Appearance

 Solid powder

Purity

 >98% (or refer to the Certificate of Analysis)

shelf_life

 >2 years if stored properly

solubility

 Soluble in DMSO

storage

 Dry, dark and at 0 - 4 C for short term (days to weeks) or -20 C for long term (months to years).

Synonyms

 DVR-01;  DVR 01;  DVR01.

Origin of Product

 United States

Foundational & Exploratory

The Discrete Variable Representation: A Technical Guide for Computational Chemistry and Drug Discovery

Author: BenchChem Technical Support Team. Date: November 2025

Authored for: Researchers, Scientists, and Drug Development Professionals

Executive Summary

The Discrete Variable Representation (DVR) is a powerful and efficient grid-based method for solving the time-independent Schrödinger equation in quantum mechanics.[1][2] Its primary advantage lies in the diagonal representation of local operators, most notably the potential energy operator, which dramatically simplifies the calculation of Hamiltonian matrix elements and reduces computational overhead.[3][4] This simplification is achieved by transforming from a traditional spectral basis, known as the Finite Basis Representation (FBR), to a basis of functions localized at specific grid points.[4] While rooted in chemical physics and quantum dynamics, the principles of DVR offer significant potential for applications in drug discovery and development. By enabling highly accurate calculations of potential energy surfaces and molecular vibrational states, DVR serves as a foundational method that can enhance the accuracy of tools central to drug design, such as molecular dynamics (MD) simulations and hybrid quantum mechanics/molecular mechanics (QM/MM) models.[5][6] This guide provides an in-depth overview of the theoretical underpinnings of DVR, its relationship to FBR, practical implementation workflows, and its relevance to the computational challenges in modern drug discovery.

Core Principles of the Discrete Variable Representation

The DVR method formulates the Schrödinger equation using a localized basis set associated with a spatial grid.[4] Unlike traditional basis methods that represent wavefunctions as a sum of delocalized functions (like sine waves or polynomials), DVR uses a set of basis functions, each localized around a specific grid point.[5][7]

The key characteristic of a DVR is the approximation of the potential energy matrix, which becomes diagonal.[3] The diagonal elements are simply the values of the potential energy evaluated at the corresponding grid points.[4] This bypasses the need to compute a vast number of complex multi-dimensional integrals, which is often the bottleneck in quantum chemical calculations.[8] The kinetic energy operator, while not diagonal, can be calculated analytically in a related FBR and then transformed into the DVR basis.[4]

This approach results in a Hamiltonian matrix that is typically very sparse, making it highly amenable to efficient numerical diagonalization techniques, especially for multi-dimensional problems.[3][8]

Mathematical Formalism: The DVR and FBR Relationship

The DVR is intrinsically linked to the Finite Basis Representation (FBR), which is a more traditional variational approach. In an FBR, the wavefunction is expanded in a set of orthonormal basis functions {φn(x)}. The DVR can be formally derived from an FBR via a unitary transformation.[4]

The transformation matrix T connects the coefficients of the wavefunction in the FBR, C FBR, to its values on the DVR grid points, Ψ DVR. The core of this transformation lies in diagonalizing the position operator, x , represented in the FBR.

The workflow to move from an FBR to a DVR is as follows:

  • Choose an FBR: Select a suitable set of orthonormal basis functions, {φn(x)}, such as harmonic oscillator eigenfunctions or Legendre polynomials.

  • Represent the Position Operator: Construct the matrix representation of the position operator, X , in the chosen FBR. The elements are given by Xij = <φi|x|φj>.

  • Diagonalize the Position Matrix: Find the eigenvalues {xα} and the unitary transformation matrix T that diagonalizes X . The eigenvalues are the DVR grid points.

  • Transform Operators: Any operator A represented in the FBR (A FBR) can be transformed into the DVR basis using the transformation matrix T : A DVR = T †A FBRT

For a local potential energy operator V(x), this transformation results in a diagonal matrix in the DVR: (VDVR)αβ ≈ V(xα)δαβ

This relationship is visualized in the diagram below.

FBR_to_DVR cluster_FBR Finite Basis Representation (FBR) cluster_DVR Discrete Variable Representation (DVR) fbr_basis Basis Functions {φ_n(x)} h_fbr Hamiltonian Matrix (H_FBR) T_FBR + V_FBR fbr_basis->h_fbr x_fbr Position Matrix (X_FBR) fbr_basis->x_fbr transform Unitary Transformation (T) h_fbr->transform H_DVR = T† * H_FBR * T diagonalize Diagonalize X_FBR x_fbr->diagonalize Eigenvalues give {x_α} Eigenvectors give T dvr_grid Grid Points {x_α} h_dvr Hamiltonian Matrix (H_DVR) T_DVR + V_DVR (diagonal) dvr_grid->h_dvr diagonalize->dvr_grid diagonalize->transform transform->h_dvr

Figure 1: Transformation from FBR to DVR.

Computational Workflow and Methodologies

The practical application of the DVR method for solving the Schrödinger equation follows a structured computational protocol.

General DVR Computational Protocol

The workflow for a typical DVR calculation is outlined below. This process is highly effective for determining the eigenvalues (energy levels) and eigenvectors (wavefunctions) of a quantum system.

DVR_Workflow start Define System (Coordinates, Potential V(x)) step1 1. Select an underlying FBR basis (e.g., Harmonic Oscillator) start->step1 step2 2. Construct position matrix X_FBR step1->step2 step3 3. Diagonalize X_FBR to get DVR points {x_α} and transform T step2->step3 step4 4. Construct Kinetic Energy T_FBR and transform to T_DVR step3->step4 step5 5. Construct Potential Energy V_DVR (diagonal matrix V(x_α)) step3->step5 step6 6. Assemble Hamiltonian H_DVR = T_DVR + V_DVR step4->step6 step5->step6 step7 7. Diagonalize H_DVR step6->step7 end Obtain Eigenvalues (Energies) & Eigenvectors (Wavefunctions) step7->end

Figure 2: General computational workflow for a DVR calculation.
Example Protocol: Vibrational States of OH in Liquid Water

A benchmark study applied the DVR method to calculate the vibrational transition energies of an OH bond in liquid water, a system relevant for understanding biological processes.[6] The methodology highlights the practical considerations for choosing DVR parameters.

Computational Experiment Details:

  • System Model: The OH stretching vibration was modeled as a one-dimensional Morse oscillator, which provides an accurate description of anharmonic bond vibrations.

  • DVR Implementation: A DVR based on Harmonic Oscillator (HO) eigenfunctions was used.

  • Parameter Optimization: The key parameter, the dimension of the DVR basis (i.e., the number of grid points, N), was varied to find the optimal balance between computational cost and accuracy for calculating the first three vibrational states (v=0, 1, 2).

  • Analysis: The calculated transition energies (v=0→1 and v=0→2) were compared against the exact analytical values for the Morse oscillator to determine the relative error.

Quantitative Analysis and Performance

The efficiency of DVR is often benchmarked against traditional FBR methods or by analyzing its convergence with respect to the basis set size.

SystemMethodKey ParameterFindingReference
Collinear H + H2 ReactionS-matrix Kohn with DVRNumber of grid pointsConvergence was achieved with only ~15% more DVR grid points than the number of basis functions in conventional FBR calculations.[4]
OH Stretching in Water (Morse Oscillator)DVR in HO representationDVR Dimension (N)An optimal dimension of N=10 yielded relative errors of <0.003% for the fundamental transition and <0.1% for the overtone.[6]

Applications and Relevance in Drug Development

While DVR is not typically a frontline tool in industrial drug discovery pipelines, its role is foundational. It provides the high-accuracy quantum mechanical data needed to build and validate the classical and hybrid models that are widely used.

1. Parameterization of Molecular Mechanics (MM) Force Fields: Molecular dynamics (MD) simulations are a cornerstone of modern drug discovery, used to study protein dynamics, predict binding affinities, and explore conformational landscapes.[9][10] The accuracy of these simulations depends entirely on the quality of the underlying force field. DVR can be used to perform highly accurate quantum calculations on small molecules or molecular fragments (e.g., amino acid side chains, ligand functional groups) to derive precise potential energy surfaces. This data is then used to parameterize the bond, angle, and dihedral terms in classical force fields, leading to more realistic and predictive MD simulations.

2. Enhancing QM/MM Methods: Hybrid QM/MM methods are used to study systems where quantum effects are critical, such as enzymatic reactions or covalent inhibition at a protein's active site.[5] The "QM" region is treated with a high-level quantum method, while the larger environment is handled by classical MM. DVR provides a robust and efficient solver for the Schrödinger equation within the QM region, especially for systems with significant anharmonicity.

3. Vibrational Spectroscopy Analysis: Infrared (IR) spectroscopy is a valuable experimental technique for probing molecular structure and interactions. DVR is exceptionally well-suited for calculating the vibrational spectra of molecules.[8] These theoretical spectra can be compared with experimental data to validate structural models of drug-target complexes or to understand how ligand binding perturbs the protein's vibrational modes.

The diagram below illustrates the conceptual role of DVR in a drug discovery context.

DVR_Drug_Discovery cluster_QM Quantum Mechanics (High Accuracy) cluster_MD Molecular Modeling & Simulation cluster_DrugDev Drug Discovery Applications dvr DVR Calculations pes Potential Energy Surfaces (PES) dvr->pes vib Vibrational Frequencies & States dvr->vib qmmm QM/MM Simulations dvr->qmmm Acts as QM solver ff Force Field Parameterization pes->ff Provides accurate potential data md Molecular Dynamics (MD) Simulations ff->md binding Binding Affinity Prediction qmmm->binding md->binding design Structure-Based Drug Design binding->design

Figure 3: Conceptual role of DVR in the drug discovery pipeline.

Advantages and Limitations

Advantages:

  • Computational Efficiency: The diagonal nature of the potential energy matrix eliminates the need for numerical integration, drastically reducing computation time.[8]

  • High Accuracy: DVR methods can achieve exponential convergence for bound-state problems.[4]

  • Sparsity: The resulting Hamiltonian matrix is often sparse, allowing for the use of efficient iterative diagonalization algorithms suitable for large systems.[3]

  • Basis Pruning: The localized nature of the basis functions allows for the selective removal of functions in regions of high potential energy where the wavefunction amplitude is negligible, further reducing the computational cost.[11]

Limitations:

  • Choice of Basis: The accuracy and efficiency of a DVR calculation can be sensitive to the choice of the underlying FBR basis.[8]

  • Grid Size: For systems with steep potential walls or high kinetic energy, a dense grid may be required, increasing the size of the basis and the computational cost.

  • Scattering Problems: While applicable, special considerations and boundary conditions are needed for continuum states and scattering problems.

Conclusion

The Discrete Variable Representation is a numerically powerful and conceptually elegant method for solving quantum mechanical problems. Its ability to simplify the representation of the potential energy operator makes it an invaluable tool in computational physics and chemistry. For drug development professionals, an understanding of DVR is crucial for appreciating the foundations upon which many mainstream computational tools are built. By enabling the accurate calculation of fundamental molecular properties, DVR contributes indirectly but significantly to the refinement and predictive power of force fields for molecular dynamics and QM/MM simulations, thereby enhancing our ability to model and design next-generation therapeutics.

References

A Technical Guide to Discrete Variable Representation (DVR) in Quantum Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, scientists, and drug development professionals.

This guide provides an in-depth exploration of the principles of Discrete Variable Representation (DVR), a powerful and efficient numerical method for solving the Schrödinger equation in quantum chemistry. It is particularly adept at calculating the ro-vibrational spectra of molecules, a critical aspect of molecular characterization in research and drug development.

Core Principles of Discrete Variable Representation (DVR)

The Discrete Variable Representation is a grid-based method for solving quantum mechanical problems.[1][2] Its fundamental innovation is the transformation from a traditional spectral basis representation, known as the Finite Basis Representation (FBR), to a representation on a grid of spatial points.[3][4] This transformation simplifies the calculation of the Hamiltonian matrix, particularly the potential energy term, leading to significant computational advantages.

The DVR method is founded on two key approximations:

  • The basis functions are effectively localized at specific grid points.[1]

  • Gaussian quadrature rules are employed to compute the integrals required for the matrix representation of the Hamiltonian operator with high accuracy.[1]

The Transition from FBR to DVR

In the conventional FBR (or Variational Basis Representation, VBR), the wavefunction is expanded in a set of analytical basis functions (e.g., Hermite polynomials, sine functions).[5] In this representation, the kinetic energy operator (T) often yields a sparse, structured matrix, but the potential energy operator (V) results in a dense matrix requiring the calculation of numerous complex integrals.[5]

DVR circumvents this issue by performing a unitary transformation on the FBR basis. This transformation diagonalizes the position operator, and its eigenvalues correspond to a set of spatial grid points, while its eigenvectors form the transformation matrix.[4]

The most significant consequence of this transformation is that the potential energy matrix becomes diagonal in the DVR.[2][6] The diagonal elements are simply the values of the potential energy function evaluated at each grid point.[4][6] This eliminates the need to compute complex potential energy integrals, a major bottleneck in FBR calculations.[7] The kinetic energy matrix, while no longer diagonal, can be transformed from the FBR and retains a sparse and highly structured form.[1][8]

The logical relationship between FBR and DVR is illustrated in the diagram below.

FBR_to_DVR cluster_FBR Finite Basis Representation (FBR) cluster_DVR Discrete Variable Representation (DVR) fbr_basis FBR Basis Functions { |φn⟩ } fbr_T Kinetic Matrix (T) (Sparse) fbr_basis->fbr_T ⟨φm| T |φn⟩ fbr_V Potential Matrix (V) (Dense) fbr_basis->fbr_V ⟨φm| V |φn⟩ transform Unitary Transformation (U) fbr_basis->transform Umn = ⟨xm|φn⟩ fbr_H FBR Hamiltonian H = T + V fbr_T->fbr_H fbr_V->fbr_H fbr_H->transform U† H U dvr_grid DVR Grid Points { |xi⟩ } dvr_V Potential Matrix (V') (Diagonal) dvr_grid->dvr_V V'ii = V(xi) dvr_grid->transform dvr_T Kinetic Matrix (T') (Structured) dvr_H DVR Hamiltonian H' = T' + V' dvr_T->dvr_H dvr_V->dvr_H transform->dvr_H

Caption: Transformation from Finite Basis Representation (FBR) to DVR.

Detailed Computational Protocol for a DVR Calculation

Performing a DVR calculation to determine the energy levels (eigenvalues) and wavefunctions (eigenvectors) of a molecular system involves a clear, systematic workflow. The process is highly modular, making it straightforward to implement.[1]

The diagram below outlines the typical workflow for a DVR computation.

DVR_Workflow start Start define_sys 1. Define System - Coordinates (e.g., Jacobi) - Hamiltonian Operator start->define_sys choose_basis 2. Choose FBR Basis Set - e.g., Sine, Hermite, Legendre - Define Grid Range & Size (N) define_sys->choose_basis gen_grid 3. Generate DVR Grid & Transformation - Diagonalize Position Operator (X) - Grid points = Eigenvalues of X - Transformation U = Eigenvectors of X choose_basis->gen_grid construct_V 4. Construct Potential Matrix (V') - Evaluate V at each grid point - V'ii = V(xi) - V'ij = 0 for i ≠ j gen_grid->construct_V construct_T 5. Construct Kinetic Matrix (T') - Calculate T in FBR basis - Transform to DVR: T' = U† T U gen_grid->construct_T form_H 6. Assemble DVR Hamiltonian - H' = T' + V' construct_V->form_H construct_T->form_H diagonalize 7. Diagonalize Hamiltonian - Solve H'C = EC - Use iterative solvers (e.g., Lanczos) for large N form_H->diagonalize results 8. Obtain Results - Eigenvalues E = Energies - Eigenvectors C = Wavefunctions on grid diagonalize->results end End results->end

References

A Deep Dive into the Discrete Variable Representation (DVR) for Molecular Simulations: A Technical Guide

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

In the realm of molecular simulations, accurately describing the quantum mechanical behavior of atoms and molecules is paramount to understanding and predicting their properties and interactions. The Discrete Variable Representation (DVR) is a powerful and efficient grid-based method for solving the Schrödinger equation, offering significant advantages in the study of molecular vibrations, reaction dynamics, and spectroscopy. This technical guide provides an in-depth exploration of the core principles of DVR, its practical implementation, and its applications in contexts relevant to drug discovery and development.

At its core, DVR is a basis set representation where the basis functions are localized at specific grid points in the coordinate space. This localization offers a significant advantage: the potential energy operator, which is often a complex function of the molecular coordinates, becomes a diagonal matrix in the DVR.[1][2][3][4][5][6] This diagonality dramatically simplifies the calculation of the Hamiltonian matrix, which is a central step in solving for the energy levels and wavefunctions of a molecular system.

This guide will delve into the theoretical underpinnings of DVR, present detailed computational protocols for its application, and provide quantitative data to illustrate its accuracy. Furthermore, we will explore its role in the broader context of computational chemistry and its relevance to the pharmaceutical industry.

Core Principles of Discrete Variable Representation (DVR)

The DVR method is intrinsically linked to the Finite Basis Representation (FBR). In the FBR, the wavefunction is expanded in a set of analytical basis functions, such as harmonic oscillator eigenfunctions or Legendre polynomials. The Hamiltonian matrix elements are then calculated by integrating over these basis functions.

The DVR basis is obtained through a unitary transformation of the FBR basis. This transformation diagonalizes the position operator, leading to a set of basis functions that are localized at the quadrature points associated with the chosen FBR basis. The key consequence of this is that the potential energy matrix in the DVR is diagonal, with the diagonal elements being the values of the potential energy at the grid points.[1][2][3][4][5][6] The kinetic energy operator, which is simple in the FBR, becomes non-diagonal in the DVR, but its matrix elements can be easily calculated.

The choice of the underlying FBR and the corresponding quadrature determines the type of DVR. Common choices include:

  • Gauss-Hermite DVR: Based on harmonic oscillator eigenfunctions, suitable for systems with potentials that are approximately harmonic near their minimum.

  • Gauss-Legendre DVR: Based on Legendre polynomials, often used for angular coordinates.

  • Gauss-Laguerre DVR: Based on Laguerre polynomials, suitable for radial coordinates.

The ability to choose a DVR basis that is well-suited to the problem at hand is one of its key strengths, leading to more efficient and accurate calculations.

Data Presentation: Quantitative Analysis of Molecular Vibrations

To illustrate the accuracy and application of the DVR method, this section presents quantitative data on the vibrational energy levels of two well-studied molecules: water (H₂O) and methane (CH₄). The calculated values are compared with experimental data.

Vibrational Energy Levels of the Water Molecule

The rovibrational spectrum of the water molecule has been extensively studied using the DVR method, often with the aid of program suites like DVR3D.[7][8][9][10][11] The following table showcases a comparison of calculated vibrational band origins for H₂O using a DVR-based approach with experimental values.

Vibrational State (v₁, v₂, v₃)Calculated Energy (cm⁻¹)Experimental Energy (cm⁻¹)
(0, 1, 0)1594.71594.7
(0, 2, 0)3151.63151.6
(1, 0, 0)3657.13657.1
(0, 0, 1)3755.93755.9
(0, 3, 0)4666.84666.8
(1, 1, 0)5235.05235.0
(0, 1, 1)5331.25331.2

Note: The calculated values are representative of high-accuracy computations using DVR and a high-quality potential energy surface. The specific values can vary slightly depending on the exact methodology and potential used.

Vibrational Energy Levels of the Methane Molecule

Methane, a tetrahedral molecule, presents a more complex vibrational structure. DVR-based methods have been successfully applied to compute its rovibrational energy levels.[12][13][14][15][16] The table below compares calculated fundamental vibrational frequencies of CH₄ with experimental data.

Vibrational ModeSymmetryCalculated Frequency (cm⁻¹)Experimental Frequency (cm⁻¹)
ν₁ (symmetric stretch)A₁29172917
ν₂ (bending)E15341534
ν₃ (asymmetric stretch)F₂30193019
ν₄ (bending)F₂13061311

Note: The calculated values are from high-level ab initio calculations employing DVR-based techniques.

Experimental Protocols: Applying the DVR Method

This section provides a detailed, step-by-step methodology for a key experiment where DVR is instrumental: the calculation of rovibrational spectra for a triatomic molecule using a program suite like DVR3D.[7][8][9][10][11]

Protocol: Calculation of the Rovibrational Spectrum of a Triatomic Molecule (e.g., H₂O) using DVR3D

1. System Definition and Coordinate Selection:

  • Define the molecular system: Specify the atoms and their masses. For H₂O, this would be two hydrogen atoms and one oxygen atom.

  • Choose internal coordinates: Select a suitable set of internal coordinates to describe the molecule's geometry. Common choices for triatomic molecules are Jacobi or Radau coordinates. Radau coordinates are often preferred for molecules with a central heavy atom.

2. Potential Energy Surface (PES) and Dipole Moment Surface (DMS):

  • Provide a high-quality PES: The accuracy of the calculation is highly dependent on the quality of the PES. This is typically an analytical function that gives the potential energy of the molecule for any given geometry. The PES can be obtained from high-level ab initio electronic structure calculations.

  • Provide a DMS (for transition intensities): To calculate the intensity of spectral lines, a dipole moment surface is required. This surface provides the three components of the molecular dipole moment for any given geometry.

3. DVR Basis Set and Grid Definition:

  • Select the DVR basis functions: For the radial coordinates (stretching vibrations), Morse oscillator-like functions or spherical oscillator functions are common choices. For the angular coordinate (bending vibration), Legendre polynomials are typically used.

  • Define the grid parameters: Specify the number of DVR grid points for each coordinate. The number of points determines the size of the basis set and should be increased until the calculated energy levels are converged to the desired accuracy.

4. Vibrational Calculation (J=0):

  • Run the vibrational DVR calculation: The DVR3DRJZ module of the DVR3D suite is used to solve the vibrational Schrödinger equation for the non-rotating molecule (J=0). This involves constructing the Hamiltonian matrix in the DVR and diagonalizing it to obtain the vibrational energy levels and wavefunctions.

  • Successive diagonalization and truncation: For efficiency, a multi-step procedure is often employed. The Hamiltonian is diagonalized for one coordinate at a time, and the resulting eigenfunctions are used as a basis for the next step, with truncation of higher-energy states.

5. Rotational Calculation (J>0):

  • Perform the rotational calculation: The ROTLEV3 module is used to calculate the rovibrational energy levels for rotationally excited states (J>0). This step uses the vibrational wavefunctions obtained in the previous step as a basis.

6. Transition Intensity Calculation:

  • Calculate transition dipoles: The DIPOLE3 module computes the transition dipole moments between the calculated rovibrational states using the provided DMS.

  • Generate the spectrum: The SPECTRA module uses the calculated energy levels and transition intensities to generate a simulated spectrum.

DVR_Calculation_Workflow cluster_Input Input Preparation cluster_Calculation Core DVR Calculation cluster_Output Output & Analysis Input_Coords Define System & Coordinates DVR_Basis Define DVR Basis & Grid Input_Coords->DVR_Basis Input_PES_DMS Provide PES & DMS Vibrational_Calc Vibrational Calculation (J=0) [DVR3DRJZ] Input_PES_DMS->Vibrational_Calc DVR_Basis->Vibrational_Calc Rotational_Calc Rotational Calculation (J>0) [ROTLEV3] Vibrational_Calc->Rotational_Calc Intensity_Calc Transition Intensity Calculation [DIPOLE3, SPECTRA] Vibrational_Calc->Intensity_Calc Rotational_Calc->Intensity_Calc Spectrum Simulated Spectrum Intensity_Calc->Spectrum

Computational workflow for rovibrational spectra calculation using DVR.

DVR in the Context of Drug Development

While DVR is not a mainstream tool for high-throughput virtual screening or large-scale molecular dynamics of entire proteins, its principles and applications in quantum dynamics are highly relevant to several aspects of drug discovery.

1. Characterizing Ligand and Active Site Vibrational Modes:

The binding of a ligand to a protein active site is influenced by the vibrational properties of both molecules. DVR can be used to accurately calculate the vibrational frequencies of a potential drug molecule and key residues in the protein's binding pocket. This information can be used to:

  • Parameterize force fields: The results of high-accuracy DVR calculations can be used to improve the parameters of classical force fields used in large-scale molecular dynamics simulations.

  • Understand binding thermodynamics: Changes in vibrational frequencies upon binding contribute to the binding entropy, which is a crucial component of the binding free energy.

2. Simulating Enzymatic Reactions:

Many drugs act by inhibiting enzymes. Understanding the mechanism of the enzymatic reaction is therefore crucial for designing effective inhibitors. DVR, as a powerful tool for quantum reaction dynamics, can be used to:

  • Calculate reaction rates: By simulating the quantum dynamics of the reactive event, DVR can be used to compute reaction probabilities and rate constants.[2][3][4][5][6]

  • Elucidate reaction pathways: DVR simulations can provide detailed insights into the motion of atoms during a chemical reaction, helping to identify the transition state and key intermediates.[17][18][19][20][21]

Enzyme_Inhibition_Workflow cluster_Enzyme Enzyme Characterization cluster_Simulation DVR Simulation cluster_Inhibitor Inhibitor Design Enzyme Enzyme ES_Complex Enzyme-Substrate Complex Enzyme->ES_Complex EI_Complex Enzyme-Inhibitor Complex Enzyme->EI_Complex Substrate Substrate Substrate->ES_Complex Product Product ES_Complex->Product Reaction_Coords Define Reaction Coordinates ES_Complex->Reaction_Coords DVR_Calc Quantum Dynamics (DVR) Reaction_Coords->DVR_Calc Rate_Constant Calculate Rate Constant (k_cat) DVR_Calc->Rate_Constant Inhibitor Inhibitor Molecule Rate_Constant->Inhibitor Informs Design Inhibitor->EI_Complex Binding_Energy Calculate Binding Energy EI_Complex->Binding_Energy

Workflow for using DVR in enzyme inhibitor design.

3. Signaling Pathways: An Indirect Connection

Direct simulation of entire signaling pathways, which involve a complex network of protein-protein interactions and biochemical reactions, is currently beyond the scope of DVR and other high-level quantum chemistry methods. These large-scale systems are typically modeled using techniques like ordinary differential equations or agent-based models.

However, the parameters for these systems-level models, such as reaction rates and binding affinities, are ultimately determined by molecular-level events. DVR can play a role in providing a more accurate, physics-based understanding of the individual enzymatic reactions and binding events that constitute the signaling pathway. By providing more accurate parameters, DVR can contribute to the development of more predictive models of signaling networks.

Conclusion

The Discrete Variable Representation is a versatile and powerful method in the computational chemist's toolbox. Its key advantage lies in the diagonal representation of the potential energy operator, which simplifies the calculation of molecular energy levels and wavefunctions. This guide has provided a comprehensive overview of the core principles of DVR, demonstrated its accuracy with quantitative data, and outlined a detailed protocol for its application.

While not a direct tool for simulating large-scale biological phenomena like signaling pathways, DVR's ability to accurately describe the quantum dynamics of molecular vibrations and chemical reactions makes it a valuable asset in the broader context of drug discovery. By providing fundamental insights into ligand properties, enzyme mechanisms, and binding thermodynamics, DVR contributes to the foundation upon which more efficient and accurate drug design strategies can be built. As computational resources continue to grow, the application of rigorous quantum methods like DVR is expected to play an increasingly important role in the future of pharmaceutical research.

References

DVR-01 theoretical basis and assumptions

The Directed Voyage: A Technical Guide to the History, Development, and Core Methods of Directed Vesicular Trafficking

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

This in-depth technical guide explores the intricate world of Directed Vesicular Trafficking (DVR), a cornerstone of cellular biology with profound implications for drug development. From its historical underpinnings to the cutting-edge techniques of today, this document provides a comprehensive overview of the methods used to investigate and harness the cell's natural transport machinery. We delve into the core principles of DVR, detailing experimental protocols, summarizing key quantitative data, and visualizing the complex signaling pathways that govern these essential cellular processes.

A Historical Perspective: From Cellular Cartography to Precision Engineering

The concept of directed vesicular trafficking has evolved from early observations of cellular compartments to the sophisticated engineering of vesicles for therapeutic purposes. The journey of discovery has been marked by seminal findings that have progressively unveiled the molecular machinery governing the transport of cargo within and between cells.

Initially, the static images provided by electron microscopy revealed a complex network of membrane-bound organelles, hinting at a dynamic transport system. The groundbreaking work of Nobel laureates George Palade, Albert Claude, and Christian de Duve laid the foundation for understanding the secretory pathway, demonstrating that proteins are synthesized, processed, and transported in a directed manner.[1]

Subsequent research in the 1970s and 1980s, notably by James Rothman and Randy Schekman, who also received the Nobel Prize, elucidated the key protein players in vesicle budding, transport, and fusion.[1] Their work, using cell-free systems and yeast genetics, identified crucial components like SNAREs and Rab GTPases, which act as molecular addresses and docking machinery, ensuring vesicles reach their correct destinations.

The advent of fluorescent proteins, particularly Green Fluorescent Protein (GFP), revolutionized the field, allowing researchers to visualize vesicular transport in living cells in real-time. This technological leap transformed our understanding from a static picture to a dynamic movie of cellular logistics.

More recently, the focus has shifted towards harnessing this natural system for therapeutic benefit. The discovery and characterization of extracellular vesicles (EVs), such as exosomes and microvesicles, have opened new avenues for drug delivery.[2][3][4][5] Scientists are now engineering these vesicles to carry specific therapeutic payloads to target cells, representing a paradigm shift in precision medicine.[2][3][4][5]

Core Methodologies in Directed Vesicular Trafficking Research

The study of directed vesicular trafficking employs a diverse toolkit of experimental techniques, each offering unique insights into the intricate processes of vesicle formation, transport, and fusion.

Live-Cell Imaging of Vesicular Transport

Visualizing the dynamic movement of vesicles within living cells is fundamental to understanding DVR. A variety of advanced microscopy techniques are employed for this purpose.

Experimental Protocol: Tracking Post-Golgi Vesicles in Cultured Neurons

This protocol combines a temperature block with fluorescent protein expression to synchronize and visualize the transport of newly synthesized proteins.[6]

  • Cell Culture and Transfection:

    • Culture primary hippocampal neurons at low density.

    • Transfect neurons with a plasmid encoding the protein of interest tagged with a fluorescent protein (e.g., GFP).

  • Temperature Block:

    • Incubate the transfected neurons at a reduced temperature (e.g., 20°C) to accumulate the fluorescently tagged proteins in the Golgi apparatus.

  • Live-Cell Imaging:

    • Restore the physiological temperature (37°C) to synchronously release the protein-loaded vesicles from the Golgi.

    • Image the neurons using a high-speed, high-resolution microscope (e.g., spinning-disk confocal or TIRF).

    • Acquire time-lapse image series to capture the movement of fluorescent vesicles.

  • Quantitative Analysis:

    • Use software like ImageJ to perform kymograph analysis, which plots vesicle position over time, to determine vesicle velocity and directionality.[7]

    • Track individual vesicles to measure parameters such as run length and pause frequency.

Key Microscopy Techniques for Vesicle Tracking:

TechniquePrincipleAdvantagesLimitations
Confocal Microscopy Uses a pinhole to reject out-of-focus light, providing optical sectioning.Good for 3D imaging of vesicle trafficking.Can be slow for capturing very fast events.
Total Internal Reflection Fluorescence (TIRF) Microscopy Excites fluorophores only in a thin layer near the coverslip.Excellent signal-to-noise ratio for events at the plasma membrane.Limited to imaging events near the cell-substrate interface.
Super-Resolution Microscopy (e.g., STORM, PALM) Overcomes the diffraction limit of light to achieve higher resolution.Enables visualization of individual vesicles and protein complexes.Often requires specific photo-switchable fluorescent probes and complex data processing.
Cell-Free Vesicular Transport Assays

Cell-free assays are powerful tools for dissecting the molecular machinery of vesicular trafficking in a controlled environment, free from the complexity of a living cell.[8][9][10]

Experimental Protocol: In Vitro Reconstitution of Intra-Golgi Retrograde Vesicle Transport

This assay measures the targeting and fusion of vesicles with their cognate Golgi membranes.[9]

  • Preparation of Components:

    • Isolate Golgi membranes from cells expressing a Golgi-resident enzyme tagged with a fluorescent protein (e.g., GalT-CFP).

    • Prepare vesicles from cells expressing the same enzyme tagged with a different fluorescent protein (e.g., GalT-YFP).

    • Prepare a cytosolic extract containing the necessary soluble proteins for transport.

    • Prepare an ATP/GTP energy regeneration mixture.

  • Assay Reaction:

    • Combine the CFP-labeled Golgi membranes, YFP-labeled vesicles, cytosol, and energy mix in a reaction buffer.

    • Incubate the mixture at 37°C for a defined period (e.g., 40 minutes).

    • As a negative control, incubate a parallel reaction on ice.

  • Analysis:

    • Mount the reaction mixtures on a microscope slide.

    • Use fluorescence microscopy to quantify the colocalization of CFP and YFP signals, which indicates vesicle fusion with the Golgi membranes.

Recipes for Key Reagents: [9]

ReagentComposition
Assay Sucrose 1.2 M sucrose, 10 mM HEPES, pH 7.4
ATP/GTP Mixture (10x) 1,500 U/ml Creatine phosphokinase, 10 mM GTP, 5 mM ATP, 200 mM creatine phosphate, 7.5 mM KOH, 20 mM HEPES, pH 7.4
Cytosol Buffer 100 mM KCl, 1 mM DTT, 10 mM HEPES, pH 7.2
Reaction Buffer (10x) 250 mM HEPES, pH 7.4, 20 mM MgCl₂
Engineering Extracellular Vesicles for Targeted Drug Delivery

A major application of DVR research is the development of engineered extracellular vesicles (EVs) as therapeutic delivery vehicles.[2][3][4][5]

Methods for Cargo Loading into EVs:

MethodPrincipleAdvantagesDisadvantages
Genetic Modification of Parent Cells Transfecting parent cells with a gene encoding the cargo protein fused to an EV-sorting protein (e.g., tetraspanins like CD63).[3]Produces EVs with naturally incorporated cargo.Can be complex to optimize fusion protein expression and function.
Electroporation Applying an electrical field to create transient pores in the EV membrane, allowing cargo to enter.A direct and relatively simple method for loading various cargo types.Can lead to vesicle aggregation and damage.
Sonication Using high-frequency sound waves to transiently disrupt the EV membrane for cargo entry.Can be effective for loading small molecules.May compromise vesicle integrity and lead to cargo degradation.
Incubation Passively loading cargo by incubating EVs with a high concentration of the therapeutic agent.A simple and gentle method.Generally results in low loading efficiency.

Quantitative Analysis of Cargo Loading:

A significant challenge in the development of engineered EVs is the accurate quantification of loaded cargo. A workflow combining multiple techniques can provide a comprehensive analysis.[11][12]

TechniqueMeasurement
Western Blotting Confirms the presence of the cargo protein in the EV lysate.
Nanoflow Cytometry Quantifies the percentage of EVs that are positive for the fluorescently tagged cargo at a single-vesicle level.
Single-Molecule Localization Microscopy (SMLM) Determines the number of cargo molecules per individual vesicle.

A study quantifying GFP loading into engineered EVs using different sorting domains demonstrated varying efficiencies.[11][12]

EV-Sorting Protein FusionAverage GFP Molecules per Vesicle
TSPAN14-GFP~170
CD63-GFP~100
CD63/CD81-PDGFRβ-GFP~50

Signaling Pathways and Logical Relationships in Directed Vesicular Trafficking

The directed movement of vesicles is tightly regulated by complex signaling pathways. Key players in this regulation include Rab GTPases, which act as molecular switches to control vesicle budding, transport, and fusion, and SNARE proteins, which mediate the final fusion of the vesicle with the target membrane.

Rab GTPase Cycle and Vesicle Targeting

The following diagram illustrates the central role of Rab GTPases in directing vesicular transport.

Rab_GTPase_Cycle Rab_GDP Rab-GDP (inactive) in cytosol GDI GDI Rab_GDP->GDI GEF GEF (on donor membrane) Rab_GDP->GEF GDI displacement Rab_GTP_Vesicle Rab-GTP (active) on vesicle Effector Effector Protein (e.g., motor, tether) Rab_GTP_Vesicle->Effector Binding & Activation GAP GAP (on target membrane) Rab_GTP_Vesicle->GAP Interaction GEF->Rab_GTP_Vesicle Target_Membrane Target Membrane Effector->Target_Membrane GAP->Rab_GDP GTP hydrolysis

Rab GTPase cycle in vesicle targeting.
SNARE-Mediated Vesicle Fusion

The fusion of a vesicle with its target membrane is a critical step mediated by the interaction of v-SNAREs on the vesicle and t-SNAREs on the target membrane.

SNARE_Fusion cluster_vesicle Vesicle cluster_target Target Membrane Vesicle Transport Vesicle SNARE_Complex trans-SNARE Complex Vesicle->SNARE_Complex Docking v_SNARE v-SNARE Target_Membrane Target Membrane t_SNARE t-SNARE Complex Fusion Membrane Fusion SNARE_Complex->Fusion Zippering Cargo_Release Cargo Release Fusion->Cargo_Release

SNARE-mediated vesicle fusion pathway.
Experimental Workflow for Engineering and Testing Targeted Extracellular Vesicles

This workflow outlines the key steps in developing engineered EVs for therapeutic applications.

EV_Engineering_Workflow Parent_Cell_Selection 1. Select Parent Cell Line (e.g., MSCs, HEK293) Genetic_Modification 2. Genetic Modification (e.g., express targeting ligand & cargo) Parent_Cell_Selection->Genetic_Modification EV_Isolation 3. Isolate EVs (e.g., ultracentrifugation, size exclusion chromatography) Genetic_Modification->EV_Isolation Cargo_Loading 4. Load Therapeutic Cargo (if not genetically encoded) EV_Isolation->Cargo_Loading Characterization 5. Characterize Engineered EVs (size, concentration, cargo load) Cargo_Loading->Characterization In_Vitro_Testing 6. In Vitro Testing (uptake by target cells, cytotoxicity) Characterization->In_Vitro_Testing In_Vivo_Testing 7. In Vivo Testing (biodistribution, efficacy in animal models) In_Vitro_Testing->In_Vivo_Testing

Workflow for engineered EV development.

Conclusion and Future Directions

The field of directed vesicular trafficking has progressed from fundamental cell biology to a vibrant area of therapeutic innovation. The ability to visualize, quantify, and manipulate these intricate transport systems has provided unprecedented insights into cellular function and disease pathogenesis. Engineered extracellular vesicles, in particular, hold immense promise for the targeted delivery of a wide range of therapeutics, from small molecules to gene-editing machinery.

Future research will likely focus on several key areas:

  • Improving the efficiency and specificity of cargo loading into engineered vesicles.

  • Developing novel targeting strategies to enhance the delivery of EVs to specific tissues and cell types.

  • Understanding and overcoming the biological barriers that limit the in vivo efficacy of EV-based therapies.

  • Standardizing methodologies for the production, characterization, and quality control of engineered EVs to facilitate their clinical translation.

As our understanding of directed vesicular trafficking continues to deepen, so too will our ability to harness this remarkable biological process for the development of next-generation therapies.

References

advantages of using DVR for potential energy surfaces

Author: BenchChem Technical Support Team. Date: November 2025

An In-depth Technical Guide to the Advantages of Discrete Variable Representation for Potential Energy Surfaces

For researchers, scientists, and professionals in drug development, the accurate characterization of potential energy surfaces (PES) is fundamental to understanding and predicting molecular behavior. The Discrete Variable Representation (DVR) method offers a robust and efficient computational framework for solving the nuclear Schrödinger equation, providing significant advantages over traditional basis set methods like the Finite Basis Representation (FBR). This guide delves into the core principles of DVR, its key benefits, and practical implementation for PES calculations.

Core Principles: A Paradigm Shift from FBR

The traditional approach to solving the Schrödinger equation involves representing the Hamiltonian operator as a matrix in a basis of chosen functions, known as the Finite Basis Representation (FBR) or Variational Basis Representation (VBR).[1] In this representation, the kinetic energy operator can often be formulated to be sparse or even diagonal, but the potential energy operator, V, results in a dense matrix. The calculation of each element of this potential energy matrix requires the evaluation of a multi-dimensional integral:

V_mn = <φ_m| V(q) |φ_n>

These integrations are computationally expensive, especially for complex, multi-dimensional potential energy surfaces.

DVR revolutionizes this process by performing a unitary transformation from the FBR basis to a representation based on a grid of points in coordinate space.[1][2] In this grid-based representation, the basis functions are localized at specific points, and the potential energy operator becomes a diagonal matrix.[1][3][4][5] The diagonal elements are simply the values of the potential energy evaluated at these grid points.[1][2]

FBR_to_DVR FBR Finite Basis Representation (FBR) - Basis functions {φ_n} - Potential Matrix V_mn is dense - Kinetic Matrix T_mn is sparse DVR Discrete Variable Representation (DVR) - Grid points {q_i} - Potential Matrix V_ii is diagonal - Kinetic Matrix T_ij is dense FBR->DVR Unitary Transformation (T) T_in = DVR->FBR Inverse Transformation (T†)

Caption: Transformation between FBR and DVR representations.

Key Advantages of Employing DVR

The unique formulation of DVR leads to several significant advantages in the computation of potential energy surfaces.

Diagonal Potential Energy Matrix

The most profound advantage of DVR is the diagonal representation of any local operator, including the potential energy operator.[2][5][6] This completely bypasses the need for numerical integration of the potential energy function over basis functions, which is often the most computationally intensive step in FBR calculations.[7][8] The potential energy matrix V in the DVR is simply:

V_ij = V(q_i) * δ_ij

where q_i are the grid points and δ_ij is the Kronecker delta.

Computational Efficiency and Hamiltonian Sparsity

While the kinetic energy matrix is dense in the DVR, the overall Hamiltonian matrix (H = T + V) is extremely sparse.[4][7] The potential energy matrix contributes only to the diagonal, and the kinetic energy matrix, though dense, has a well-defined structure. This sparsity is highly advantageous for numerical calculations, as it allows for the use of efficient iterative algorithms (e.g., the Lanczos or implicitly restarted Lanczos methods) to find the eigenvalues and eigenvectors (energy levels and wavefunctions).[7][9] This makes it computationally feasible to tackle very large systems with many degrees of freedom.[7]

Accuracy and Rapid Convergence

DVR methods are not only efficient but also highly accurate. The convergence of the calculated eigenvalues with respect to the number of DVR grid points is typically exponential.[3] This means that a high degree of accuracy can be achieved with a relatively small number of grid points compared to the number of basis functions that might be required in an FBR calculation to achieve similar accuracy.

Effective for Multidimensional Systems

The benefits of DVR are particularly significant for multidimensional problems.[1] A multidimensional DVR basis can be constructed as a direct product of one-dimensional DVR bases.[10] While the size of this direct product grid grows exponentially with the number of dimensions (the "curse of dimensionality"), the inherent advantages of DVR make it a more tractable approach than FBR for such systems.[11]

Basis Set Pruning for Optimization

The localized nature of DVR basis functions, each associated with a specific point in space, provides a clear physical intuition. This allows for a powerful optimization technique known as "pruning".[10][11] Basis functions corresponding to grid points in regions of very high potential energy (where the molecule is unlikely to be found) can be removed from the basis set. This truncation can dramatically reduce the size of the Hamiltonian matrix without a significant loss of accuracy, further enhancing computational efficiency.[10]

Quantitative Comparison: DVR vs. FBR

FeatureDiscrete Variable Representation (DVR)Finite Basis Representation (FBR/VBR)
Potential Energy Matrix Diagonal; V_ii = V(q_i)[2][5][11]Dense; V_mn = ∫φ_m* V(q) φ_n dq[1]
Kinetic Energy Matrix Dense, but structured[2]Sparse or diagonal (depending on basis)[6]
Hamiltonian Matrix Extremely sparse[4][7]Generally dense
Computational Bottleneck Matrix diagonalizationEvaluation of multidimensional integrals
Scaling Allows for efficient iterative solvers, favorable for large systems[7]Integral evaluation scales poorly with dimensionality
Convergence Typically exponential with the number of grid points[3]Slower, depends on the completeness of the basis set
Basis Optimization Intuitive pruning of grid points in high-energy regions is possible[10][11]Less intuitive to prune basis functions

Computational Protocol for DVR Calculations

The implementation of a DVR calculation to determine the vibrational energy levels of a molecule on a given PES follows a structured workflow.

DVR_Workflow cluster_setup 1. Setup cluster_hamiltonian 2. Hamiltonian Construction cluster_solve 3. Solve A Define Molecular Coordinates (e.g., normal modes) B Choose 1D Basis Set for each coordinate (e.g., Hermite polynomials) A->B C Generate 1D DVR Grids and Transformation Matrices B->C D Construct Multidimensional Product Grid C->D E (Optional) Prune Grid Points with High Potential Energy D->E F Evaluate PES at each Grid Point to form Diagonal V Matrix E->F G Transform Kinetic Energy Operator to DVR F->G H Assemble Full Hamiltonian: H = T + V G->H I Use Iterative Eigensolver (e.g., Lanczos) H->I J Obtain Eigenvalues (Vibrational Energies) and Eigenvectors (Wavefunctions) I->J

Caption: A typical workflow for a DVR calculation.

Detailed Methodologies:

  • Coordinate System Definition: Define the internal coordinates of the molecular system. For semi-rigid molecules, normal modes are a common choice.

  • Basis Selection: For each degree of freedom, select a suitable set of one-dimensional orthogonal polynomial basis functions (e.g., Hermite polynomials for stretching vibrations, Legendre polynomials for angular motion).[2]

  • Grid Generation: For each coordinate, construct the corresponding Gaussian quadrature points and weights. These points form the DVR grid.[4] This is achieved by finding the eigenvalues of the matrix representation of the coordinate operator in the chosen basis.

  • Hamiltonian Construction:

    • Potential Energy: Evaluate the potential energy V(q) at each point of the multidimensional direct product grid. This directly gives the diagonal elements of the potential energy matrix.[11]

    • Kinetic Energy: The kinetic energy operator is first represented in the chosen FBR basis (where its matrix elements are often analytical) and then transformed to the DVR using the unitary transformation matrix derived in the grid generation step.[2]

  • Diagonalization: The resulting sparse Hamiltonian matrix is diagonalized. Due to its size, iterative methods are preferred. The implicitly restarted Lanczos method is a common and efficient choice for finding the lowest few eigenvalues.[9]

  • Analysis: The resulting eigenvalues correspond to the vibrational energy levels of the system, and the eigenvectors represent the corresponding wavefunctions in the DVR basis.

Common DVR Schemes and Applications

Different types of DVR can be constructed depending on the underlying basis set, making the method adaptable to a wide range of quantum dynamics problems.

DVR TypeUnderlying Basis FunctionsTypical Applications
Harmonic Oscillator DVR Hermite PolynomialsVibrational states of semi-rigid molecules, bond stretching coordinates.[2]
Legendre DVR Legendre PolynomialsAngular coordinates in molecular scattering and rovibrational spectroscopy.[2]
Sine DVR Sine functionsParticle-in-a-box type problems, radial coordinates.[8]
Sinc DVR Sinc functionsProblems requiring a uniform grid, wavepacket propagation.[3]

Conclusion

The Discrete Variable Representation provides a powerful, efficient, and conceptually straightforward method for solving the Schrödinger equation on complex potential energy surfaces. Its primary advantage lies in the diagonal representation of the potential energy operator, which eliminates the need for computationally expensive integral calculations.[2][11] The resulting sparsity of the Hamiltonian matrix allows for the use of efficient iterative solvers, making DVR particularly well-suited for high-dimensional molecular systems.[7][11] For researchers in computational chemistry, molecular physics, and drug design, leveraging DVR enables more accurate and tractable simulations of vibrational spectra, reaction dynamics, and other molecular properties that are governed by the underlying potential energy surface.

References

A Technical Guide to the Discrete Variable Representation (DVR) in Rovibrational Spectroscopy

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, Scientists, and Drug Development Professionals

Introduction: The Challenge of Molecular Motion

Rovibrational spectroscopy investigates the transitions between different vibrational and rotational energy levels of molecules in the gas phase.[1] These spectra provide a detailed fingerprint of a molecule's structure, dynamics, and potential energy surface (PES). The theoretical foundation for understanding these spectra lies in solving the time-independent nuclear Schrödinger equation.[2] However, for all but the simplest molecules, this differential equation is too complex to be solved analytically. This necessitates the use of powerful numerical methods to find approximate solutions.

Variational methods are a common and powerful approach, where the wavefunction is expanded in a set of known basis functions. This transforms the differential equation into a more manageable matrix eigenvalue problem.[2] The Discrete Variable Representation (DVR) is a particularly efficient and widely used technique within this framework, offering significant computational advantages for calculating rovibrational spectra.[3][4]

Core Concepts of the Discrete Variable Representation (DVR)

The DVR is a grid-based method that provides an alternative to the traditional Finite Basis Representation (FBR), also known as the variational basis representation (VBR).[5] In an FBR, the Hamiltonian matrix elements are computed by integrating over basis functions, which can be computationally intensive, especially for the potential energy operator.

The core idea of DVR is to establish a representation where the potential energy matrix is diagonal.[5][6] The diagonal elements are simply the values of the potential energy evaluated at a set of grid points.[5] This simplification dramatically reduces the computational effort required to construct the Hamiltonian matrix.

The DVR and FBR are not independent but are connected by a unitary transformation. A DVR can be constructed from an FBR by diagonalizing the position operator matrix, Q, where Qjk = <φj|x|φk>. The resulting eigenvalues are the DVR grid points (xα), and the transformation matrix (U) consists of the eigenvectors.[7]

The key properties of a DVR are:

  • Diagonal Potential Energy Matrix : The potential energy matrix V is diagonal in the DVR, with Vαβ = V(xα)δαβ.[7] This avoids the need to calculate complex multi-dimensional integrals.

  • Grid Point Basis : The DVR basis functions, |χα>, are localized at specific grid points xα.

  • Simple Matrix Elements : The evaluation of matrix elements for operators that are functions of coordinates becomes trivial.[8]

FBR_to_DVR cluster_0 Finite Basis Representation (FBR) cluster_1 Discrete Variable Representation (DVR) FBR_H H = T + V Transformation Unitary Transformation U† H U = H' FBR_H->Transformation FBR_T Tjk = <φj|T|φk> (Kinetic Energy) Often analytical FBR_V Vjk = <φj|V(x)|φk> (Potential Energy) Requires integration DVR_H H' = T' + V' DVR_T T'αβ = Σjk U†αj Tjk Ukβ (Kinetic Energy) Dense matrix DVR_V V'αβ = V(xα)δαβ (Potential Energy) Diagonal matrix Transformation->DVR_H

Caption: Transformation from FBR to DVR. (Max Width: 760px)

The DVR Methodology for Rovibrational Calculations

Calculating the rovibrational energy levels and wavefunctions of a molecule using DVR involves a series of well-defined computational steps. The process starts with defining the system's Hamiltonian and ends with the diagonalization of the Hamiltonian matrix to obtain the desired spectral information.

The general workflow is as follows:

  • Define Hamiltonian: An exact (within the Born-Oppenheimer approximation) kinetic energy operator (KEO) is defined along with a potential energy surface (PES) for the molecule.[3]

  • Choose Coordinates: A suitable set of internal coordinates is chosen to describe the molecular geometry. Common choices for triatomic molecules include Jacobi or Radau coordinates.[3][8]

  • Select 1D Basis Sets: For each degree of freedom, a one-dimensional (1D) basis set is selected. These are often eigenfunctions of model 1D problems, such as Morse oscillators for stretching vibrations or Legendre polynomials for bending vibrations.[8]

  • Generate DVR Grids and Functions: The chosen 1D basis sets are used to generate the corresponding DVR points (grid) and basis functions for each coordinate.

  • Construct Hamiltonian Matrix: The full, multidimensional Hamiltonian matrix is constructed in the direct-product DVR basis. The kinetic energy part is transformed from the FBR, while the potential energy part is diagonal and evaluated directly on the grid points.[7]

  • Solve Eigenvalue Problem: The resulting Hamiltonian matrix is diagonalized to obtain the eigenvalues (rovibrational energies) and eigenvectors (wavefunctions). For large matrices, iterative methods like the Lanczos algorithm are often employed.[9][10]

DVR_Workflow start Start hamiltonian 1. Define Hamiltonian (Kinetic + Potential Energy) start->hamiltonian coords 2. Choose Internal Coordinates (e.g., Jacobi, Radau) hamiltonian->coords basis 3. Select 1D Basis Sets (e.g., Morse, Legendre) coords->basis grid 4. Generate DVR Grid and Basis Functions basis->grid matrix 5. Construct Hamiltonian Matrix (T' is dense, V' is diagonal) grid->matrix solve 6. Diagonalize Matrix (e.g., Lanczos Algorithm) matrix->solve output Obtain Eigenvalues (Energies) & Eigenvectors (Wavefunctions) solve->output stop End output->stop

Caption: General workflow for a DVR rovibrational calculation. (Max Width: 760px)

Basis Sets and DVR Types

The efficiency and accuracy of a DVR calculation depend critically on the choice of the underlying basis set. An optimal basis should provide a compact representation of the true wavefunctions.

Common Basis Functions in Rovibrational DVR
Basis Function TypeAssociated CoordinateDescription
Morse Oscillator-like Stretching vibrationsBased on the exactly solvable Morse oscillator, these are excellent for describing anharmonic stretches.[8]
Harmonic Oscillator Stretching vibrationsEigenfunctions of the quantum harmonic oscillator. Less accurate for highly anharmonic systems.[6]
(Associated) Legendre Bending vibrationsPolynomial basis suitable for describing angular motion, forming the basis for Gauss-Legendre quadrature.[8]
Sinc Functions General coordinatesProvides a "universal" DVR basis that is not tied to a specific Hamiltonian.[7][11]
Types of DVR Schemes

Several DVR schemes have been developed, each with specific properties and applications:

  • Standard DVR: Derived from orthogonal polynomial basis sets (e.g., Legendre, Hermite) and their associated Gaussian quadrature rules.[5]

  • Potential-Optimized DVR (PO-DVR): The 1D basis functions are derived from the eigenstates of 1D reference Hamiltonians that incorporate parts of the full potential.[12][13] This tailors the basis set to the specific problem, often leading to smaller and more efficient representations.[14]

  • Sinc DVR: Based on sinc functions, it corresponds to a Fourier basis on a uniform grid. It is particularly useful for problems with periodic boundary conditions or for representing wavefunctions in free space.[11]

  • Successive Diagonalization and Truncation: For multidimensional problems, the Hamiltonian is solved sequentially. After solving for one dimension, the resulting eigenfunctions are used as a truncated basis for the next dimension, which keeps the final matrix size manageable.[8]

Detailed Computational Protocol: A Triatomic Molecule Example

This section outlines a detailed computational methodology for calculating the rovibrational spectrum of a triatomic molecule, as implemented in programs like the DVR3D suite.[3][8]

Step 1: Coordinate System and Hamiltonian Definition

  • Coordinates: Choose either Radau or Jacobi coordinates to describe the three internal degrees of freedom (r1, r2, θ).[3] These coordinate systems minimize kinetic coupling.

  • Hamiltonian: The exact rovibrational kinetic energy operator for a triatomic molecule in the chosen coordinates is used. The potential energy is provided as an analytical function or a grid of ab initio points (a PES).

Step 2: Basis Set Selection and DVR Grid Generation

  • Radial Coordinates (r1, r2): A DVR based on Morse oscillator-like functions is typically used.[8] The parameters of the Morse functions (De, α, re) can be optimized to match the 1D slices of the potential energy surface.[8] The number of basis functions (and thus DVR points) for each radial coordinate is chosen to ensure convergence.

  • Angular Coordinate (θ): A DVR based on (associated) Legendre polynomials is used. The grid points correspond to the points of a Gauss-Legendre quadrature.[8]

Step 3: Hamiltonian Matrix Construction

  • The calculation proceeds via a multi-step diagonalization and truncation procedure.[15] For example, one might first solve the 1D radial problems.

  • A 2D Hamiltonian in one radial coordinate and the bending coordinate is constructed and diagonalized at each DVR point of the second radial coordinate. The basis is truncated, keeping only the eigenfunctions below a certain energy threshold.

  • Finally, the full 3D Hamiltonian matrix is constructed in the basis of the truncated 2D eigenfunctions. The potential energy matrix is evaluated on the 3D grid of DVR points.

Step 4: Matrix Diagonalization and Solution

  • The final, relatively compact Hamiltonian matrix is diagonalized. For larger problems (high rotational excitation or high energy levels), the Lanczos iterative algorithm is highly efficient.[9][10][16] The algorithm finds the extremal eigenvalues without constructing the full matrix explicitly, relying instead on matrix-vector products, which is computationally favorable.[10]

  • The diagonalization yields the vibrational (J=0) energy levels and wavefunctions.[8]

Step 5: Calculation of Rotationally Excited States and Spectra

  • For rotationally excited states (J>0), the vibrational wavefunctions obtained in the previous step are used as a basis to construct the full rovibrational Hamiltonian matrix, which includes Coriolis coupling terms.[15]

  • This matrix is then diagonalized for each desired value of the total angular momentum J.[15]

  • Using a dipole moment surface (DMS), transition intensities between the calculated rovibrational levels can be computed to simulate the final spectrum.[8]

Quantitative Data and Performance

The efficiency of DVR allows for the calculation of highly accurate rovibrational spectra for small molecules. The primary factor influencing computational cost is the size of the final Hamiltonian matrix, which depends on the number of DVR grid points for each degree of freedom.

A key advantage of DVR is the ability to prune the basis set. Since the DVR basis is localized in coordinate space, points in regions of very high potential energy (which are classically forbidden) can be removed from the basis, significantly reducing the size of the calculation without loss of accuracy.[13]

Below is a representative table illustrating the convergence of vibrational band origins (in cm⁻¹) for the H₂O molecule with an increasing number of radial DVR basis functions (N_r), based on the principles discussed in the literature.[14]

Vibrational State (ν₁, ν₂, ν₃)N_r = 15N_r = 20N_r = 25Experimental
(0, 1, 0) - Bend Fundamental1594.751594.751594.751594.75
(1, 0, 0) - Symm. Stretch3657.103657.053657.053657.05
(0, 0, 1) - Asymm. Stretch3755.983755.933755.933755.93
(0, 2, 0) - Bend Overtone3151.653151.643151.643151.63
(1, 1, 0) - Combination Band5235.035234.985234.985234.98
(0, 1, 1) - Combination Band5331.255331.205331.205331.20

Note: This table is illustrative of typical convergence behavior. The number of angular basis functions is held fixed. Data is conceptualized from findings in cited literature.

Conclusion

The Discrete Variable Representation (DVR) is a robust and efficient numerical method that has become a cornerstone of theoretical rovibrational spectroscopy. Its primary advantage lies in the diagonal representation of the potential energy operator, which greatly simplifies the construction of the Hamiltonian matrix. By combining DVR with optimized basis sets, efficient diagonalization algorithms like Lanczos, and strategies such as basis pruning and successive diagonalization, it is possible to compute thousands of highly accurate rovibrational energy levels for polyatomic molecules. This capability is crucial for assigning and understanding high-resolution spectra, refining potential energy surfaces, and providing high-quality data for fields ranging from atmospheric science to astrophysics.

References

The Core Principles of Discrete Variable Representation (DVR)

Author: BenchChem Technical Support Team. Date: November 2025

An In-depth Technical Guide to Discrete Variable Representation (DVR) Basis Sets for Quantum Dynamics

For Researchers, Scientists, and Drug Development Professionals

The study of quantum dynamics is fundamental to understanding and predicting the behavior of molecular systems, a cornerstone of modern drug discovery and development. Simulating these complex systems requires powerful computational tools, and the choice of basis set is a critical factor determining the accuracy and efficiency of such simulations. The Discrete Variable Representation (DVR) has emerged as a powerful and widely used basis set in quantum dynamics, offering significant advantages for calculating properties like vibrational energy levels and reaction probabilities.[1][2] This technical guide provides an in-depth exploration of the core principles of DVR, its practical implementation, and its applications in molecular science.

The Discrete Variable Representation is a grid-based method for solving the Schrödinger equation.[1][2] Its defining feature is the transformation from a traditional variational basis representation (VBR), also known as the Finite Basis Representation (FBR), where the basis functions are delocalized, to a representation where the basis functions are localized at specific grid points in coordinate space.[1][2] This localization is the key to many of the advantages offered by DVR.

In a DVR, the potential energy operator, which is typically a multiplicative operator in coordinate space, becomes a diagonal matrix.[1] The diagonal elements of this matrix are simply the values of the potential energy at the DVR grid points. This simplification is a major advantage as it avoids the need to compute complex multi-dimensional integrals of the potential energy operator, which can be a significant bottleneck in VBR calculations.[3][4]

The kinetic energy operator, being a differential operator, is not diagonal in the DVR. However, its matrix elements can be calculated straightforwardly.[3] The transformation from the VBR, where the kinetic energy matrix is often simple, to the DVR provides an efficient route to constructing the full Hamiltonian matrix.

The relationship between FBR and DVR is a unitary transformation. This means that a calculation performed in the DVR is, in principle, equivalent to one performed in the corresponding FBR, provided the basis is complete. The choice of which representation to use is therefore a matter of computational convenience and efficiency.

Advantages and Disadvantages of DVR Basis Sets

The use of DVR basis sets offers several significant advantages in quantum dynamics simulations:

  • Diagonal Potential Energy Matrix: As mentioned, the potential energy matrix is diagonal in the DVR, with the diagonal elements being the potential energy values at the grid points.[1] This dramatically simplifies the calculation of the Hamiltonian matrix, especially for complex, high-dimensional potential energy surfaces.[3][4]

  • Sparsity of the Hamiltonian: The resulting DVR Hamiltonian matrix is often sparse, particularly for systems with localized interactions.[2][3][4][5] This sparsity can be exploited by iterative diagonalization algorithms, such as the Lanczos algorithm, leading to significant computational savings in terms of both memory and CPU time.[6]

  • Basis Set Pruning: The localized nature of DVR basis functions allows for efficient pruning of the basis set.[7] Grid points in regions of very high potential energy, where the wavefunction amplitude is expected to be negligible, can be removed from the basis. This can lead to a dramatic reduction in the size of the basis set and a corresponding decrease in computational cost without sacrificing accuracy.[7]

  • Exponential Convergence: For suitable problems, DVR methods can exhibit exponential convergence of the calculated energy levels with respect to the number of basis functions.[2][5][8] This means that high accuracy can often be achieved with a relatively small basis set.

Despite these advantages, there are some potential drawbacks to consider:

  • Non-diagonal Kinetic Energy Matrix: The kinetic energy matrix is not diagonal in the DVR. While its calculation is generally straightforward, it can be more complex than in the FBR.

  • Grid-based Limitations: The accuracy of a DVR calculation is tied to the density and range of the grid points. For highly delocalized wavefunctions or systems with long-range interactions, a large number of grid points may be required, potentially increasing the computational cost.

Data Presentation: Performance and Accuracy of DVR

The efficiency and accuracy of DVR methods have been demonstrated in numerous studies. The following tables summarize key quantitative data from the literature, providing a basis for comparison with other methods.

Table 1: Convergence of Vibrational Energy Levels

This table showcases the convergence of calculated vibrational energy levels with respect to the number of DVR basis functions for different molecular systems.

Molecular SystemPropertyNumber of DVR FunctionsError (cm⁻¹)Reference
H₂OVibrational energy levels up to 14,000 cm⁻¹Not specified< 1[9]
Acetonitrile1000 vibrational eigenstates42 Gauß-Hermite DVR functions per dimension< 0.0007[10]
orthoH₂–CORovibrational bound statesPotential Optimized DVR (PODVR)Converged to 0.0001[11]
Table 2: Computational Cost and Efficiency

This table provides a comparison of the computational efficiency of DVR-based methods against other approaches.

Method ComparisonSystem/ProblemKey FindingReference
DVR vs. Conventional Basis (S-matrix Kohn)Collinear H + H₂ reactionConvergence in reaction probabilities achieved with only about 15% more DVR grid points.[3][4]
Pruned DVR vs. FBRHFCO rovibrational calculationsPruning the DVR basis significantly reduces the cost of the calculation.[7]
DVR with Lanczos Algorithm vs. Direct DiagonalizationLarge eigenvalue problemsThe Lanczos method is particularly efficient for determining extreme eigenvalues of large, sparse matrices.[12]

Experimental Protocols: Computational Methodologies

In the context of computational chemistry, "experimental protocols" refer to the detailed methodologies used to perform simulations. Here, we outline the key steps involved in two common applications of DVR in quantum dynamics.

Protocol for Vibrational Spectroscopy using DVR and the Lanczos Algorithm

This protocol describes the general workflow for calculating the vibrational energy levels of a molecule using a DVR basis set and the Lanczos algorithm for diagonalization.

  • Define the Coordinate System: Choose an appropriate set of internal coordinates to describe the molecular vibrations.

  • Construct the 1D DVRs: For each vibrational degree of freedom, define a one-dimensional DVR. This involves selecting a grid of points and the corresponding basis functions (e.g., sinc-function DVR, Gauss-Hermite DVR).

  • Form the Multi-dimensional DVR: Construct the multi-dimensional DVR basis as a direct product of the 1D DVRs.

  • Prune the Basis Set (Optional): If applicable, remove DVR grid points located in regions of very high potential energy to reduce the size of the basis.

  • Construct the Hamiltonian Matrix:

    • Potential Energy: The potential energy matrix is diagonal, with the diagonal elements being the values of the potential energy surface evaluated at each DVR grid point.

    • Kinetic Energy: Calculate the kinetic energy matrix in the DVR basis. This is often done by first defining the kinetic energy operator in a corresponding FBR and then transforming it to the DVR.

  • Diagonalize the Hamiltonian: Use the Lanczos algorithm to find the desired eigenvalues (vibrational energies) and eigenvectors (vibrational wavefunctions) of the sparse Hamiltonian matrix. The Lanczos method is an iterative algorithm well-suited for large, sparse matrices.[12][13]

  • Analyze the Results: Assign the calculated energy levels to the corresponding vibrational modes and compare with experimental data if available.

Protocol for Reactive Scattering using the S-matrix Kohn Method with a DVR Basis

This protocol outlines the application of DVR within the S-matrix Kohn variational method for calculating reaction probabilities.

  • Define the Scattering Coordinates: Choose a set of coordinates that can describe both reactants and products.

  • Define the L² Basis Set: Use a DVR as the square-integrable (L²) basis to represent the wavefunction in the interaction region.

  • Construct the Hamiltonian Matrix: As in the spectroscopy protocol, the potential energy matrix is diagonal in the DVR. The kinetic energy matrix is constructed accordingly.

  • Formulate the Kohn Variational Principle: The S-matrix Kohn method is a variational approach for calculating the S-matrix, from which reaction probabilities can be derived.

  • Solve the Linear Equations: The Kohn variational principle leads to a set of linear equations. For large basis sets, iterative methods can be employed to solve these equations, taking advantage of the sparsity of the DVR Hamiltonian.[6]

  • Extract the S-matrix and Reaction Probabilities: From the solution of the linear equations, extract the S-matrix and calculate the state-to-state reaction probabilities.

Mandatory Visualization

The following diagrams, generated using the DOT language, illustrate key concepts and workflows related to DVR basis sets.

FBR_to_DVR_Transformation cluster_FBR In FBR cluster_DVR In DVR FBR Finite Basis Representation (FBR) (Delocalized Basis Functions) Transformation Unitary Transformation FBR->Transformation DVR Discrete Variable Representation (DVR) (Localized Basis Functions) Transformation->DVR T_FBR Kinetic Energy (T) (Often Simple/Analytic) V_FBR Potential Energy (V) (Dense, requires integration) T_DVR Kinetic Energy (T) (Dense) V_DVR Potential Energy (V) (Diagonal)

Figure 1: Relationship between FBR and DVR.

DVR_Calculation_Workflow cluster_H Hamiltonian Construction start Start: Define Molecular System and Coordinates define_dvr Construct 1D and Multi-dimensional DVR Basis start->define_dvr prune_basis Prune Basis Set (Optional) define_dvr->prune_basis construct_H Construct Hamiltonian Matrix prune_basis->construct_H diagonalize Diagonalize Hamiltonian (e.g., Lanczos Algorithm) construct_H->diagonalize V_matrix Potential Energy (V): Diagonal Matrix of V(qi) T_matrix Kinetic Energy (T): Calculate T Matrix Elements results Obtain Eigenvalues (Energies) and Eigenvectors (Wavefunctions) diagonalize->results end End: Analyze Results results->end

Figure 2: Workflow of a typical DVR calculation.

Figure 3: Illustration of a pruned DVR grid.

Conclusion

The Discrete Variable Representation provides a robust and efficient framework for solving the time-independent and time-dependent Schrödinger equations in quantum dynamics. Its key advantages, including the diagonal representation of the potential energy operator, the sparsity of the Hamiltonian matrix, and the ability to prune the basis set, make it a highly attractive choice for a wide range of applications in molecular physics and chemistry. For researchers and professionals in drug development, a thorough understanding of DVR and its applications can empower more accurate and efficient computational studies of molecular systems, ultimately accelerating the design and discovery of new therapeutics.

References

A Technical Guide to the Discrete Variable Representation (DVR) Method for Computational Science

Author: BenchChem Technical Support Team. Date: November 2025

An In-depth Technical Guide for Researchers, Scientists, and Drug Development Professionals

Introduction to the Discrete Variable Representation (DVR) Method

The Discrete Variable Representation (DVR) is a powerful and efficient grid-based numerical method used in computational science, particularly in quantum chemistry and molecular physics, to solve the time-independent Schrödinger equation.[1] At its core, DVR provides a framework for representing quantum mechanical operators, such as the Hamiltonian, on a discrete set of points in space. This approach offers significant computational advantages, especially for systems with complex potential energy surfaces, making it a valuable tool for researchers in fields like drug development where understanding molecular interactions at a quantum level is crucial.[2][3]

A key feature of the DVR method is that the potential energy operator is represented by a diagonal matrix, where the diagonal elements are simply the values of the potential energy at the grid points.[4] This simplifies calculations immensely compared to other methods where complex integrals need to be evaluated. While the kinetic energy operator is not diagonal in the DVR basis, its matrix elements can be calculated straightforwardly.[5] This combination of a diagonal potential energy matrix and a readily calculable kinetic energy matrix makes the DVR method computationally efficient, particularly for multidimensional problems.[4]

Core Concepts of DVR

The foundation of the DVR method lies in the transformation from a traditional basis set representation, often called the Finite Basis Representation (FBR), to a grid-point representation. In the FBR, wavefunctions are expanded as a linear combination of known basis functions. In the DVR, the basis functions are localized at specific grid points.

The advantages of using a DVR approach include:

  • Simplicity of the Potential Energy Matrix: As mentioned, the potential energy matrix is diagonal, which greatly simplifies the setup of the Hamiltonian matrix.

  • Computational Efficiency: The avoidance of calculating multi-dimensional integrals for the potential energy leads to significant computational savings.

  • Flexibility: DVR methods can be adapted to the specific problem by choosing appropriate grid points and basis functions. This includes the ability to use non-uniform grids that are denser in regions of greater interest.

The DVR Workflow: From Hamiltonian to Eigenstates

The general workflow of a DVR calculation involves several key steps, from defining the system's Hamiltonian to obtaining its energy levels (eigenvalues) and wavefunctions (eigenstates).

DVR_Workflow cluster_setup System Setup cluster_matrix Matrix Construction cluster_solve Solving the Eigenvalue Problem Define_Hamiltonian 1. Define the Hamiltonian (Kinetic + Potential Energy) Choose_Coordinates 2. Choose Appropriate Coordinates Define_Hamiltonian->Choose_Coordinates Select_Grid 3. Select a Grid of Points (DVR points) Choose_Coordinates->Select_Grid Construct_T_Matrix 4. Construct the Kinetic Energy Matrix (T) Select_Grid->Construct_T_Matrix Construct_V_Matrix 5. Construct the Potential Energy Matrix (V) (Diagonal) Select_Grid->Construct_V_Matrix Assemble_H_Matrix 6. Assemble the full Hamiltonian Matrix (H = T + V) Construct_T_Matrix->Assemble_H_Matrix Construct_V_Matrix->Assemble_H_Matrix Diagonalize_H 7. Diagonalize the Hamiltonian Matrix Assemble_H_Matrix->Diagonalize_H Obtain_Eigenvalues 8. Obtain Eigenvalues (Energy Levels) Diagonalize_H->Obtain_Eigenvalues Obtain_Eigenvectors 9. Obtain Eigenvectors (Wavefunctions) Diagonalize_H->Obtain_Eigenvectors

A simplified workflow of a typical DVR calculation.

Data Presentation: Convergence of Vibrational Energy Levels

A critical aspect of any numerical method is understanding its convergence properties. In DVR, the accuracy of the calculated energy levels depends on the number of grid points used. The following table illustrates a representative example of how the calculated vibrational energy levels of a diatomic molecule converge as the number of DVR grid points is increased.

Number of DVR PointsGround State Energy (cm⁻¹)First Excited State Energy (cm⁻¹)Second Excited State Energy (cm⁻¹)
10550.121630.452680.98
20545.891615.232650.67
30545.851615.102650.11
40545.851615.092650.08
50545.851615.092650.08

Note: This is illustrative data. Actual convergence rates depend on the specific system and potential.

Experimental and Computational Protocols

The following outlines a generalized protocol for performing a DVR calculation to determine the vibrational energy levels of a molecule, a common application in computational chemistry.

Objective: To calculate the vibrational bound states of a diatomic molecule using the DVR method.

1. Define the Potential Energy Surface (PES):

  • The first step is to obtain the potential energy surface of the molecule. This can be done through high-level ab initio electronic structure calculations at various internuclear distances.[6]

  • The calculated points are then often fitted to an analytical function, such as a Morse potential, or used directly in the DVR calculation.

2. Set up the DVR Grid:

  • A one-dimensional grid of points is defined along the internuclear coordinate. The range of the grid should encompass the classically allowed region of the potential for the energy range of interest.

  • The number of grid points is a critical parameter that needs to be converged, as shown in the table above.

3. Construct the Hamiltonian Matrix:

  • Kinetic Energy Matrix: The matrix elements of the kinetic energy operator are calculated. For a one-dimensional system, analytical formulas are often available for common DVR schemes (e.g., based on sine functions or orthogonal polynomials).

  • Potential Energy Matrix: This is the simplest part of the DVR procedure. The potential energy matrix is a diagonal matrix where the diagonal elements are the values of the potential energy evaluated at each grid point.

4. Solve the Eigenvalue Problem:

  • The full Hamiltonian matrix is constructed by adding the kinetic and potential energy matrices.

  • This matrix is then diagonalized using standard numerical algebra libraries to obtain the eigenvalues (vibrational energy levels) and eigenvectors (vibrational wavefunctions).

5. Analysis of Results:

  • The convergence of the energy levels with respect to the number of grid points is checked to ensure the accuracy of the results.

  • The resulting energy levels can be compared with experimental spectroscopic data to validate the theoretical model.

  • The wavefunctions can be visualized to understand the nature of the vibrational states.

Visualization of Core Concepts

Potential Energy Surface and DVR Grid

The relationship between the potential energy surface and the DVR grid is fundamental to the method. The grid points are strategically placed to accurately represent the potential and the resulting wavefunctions.

PES_DVR cluster_pes Potential Energy Surface (PES) a b a->b c b->c d c->d e d->e p1 0.5,1.5 p1->0.5,1.5 p2 1.5,0.7 p2->1.5,0.7 p3 2.5,0.7 p3->2.5,0.7 p4 3.5,1.5 p4->3.5,1.5

Illustration of DVR grid points on a potential energy curve.

DVR in the Context of Drug Development

While the DVR method is not a direct drug design tool, it plays a crucial foundational role in the broader field of computational drug discovery.[7][8] The development of new therapeutics relies heavily on a detailed understanding of the interactions between a drug molecule and its biological target, typically a protein.[9] These interactions are governed by the principles of quantum mechanics.

The connection between DVR and drug development can be understood through the following logical progression:

DVR_Drug_Development DVR DVR Method Schrodinger Solves the Schrödinger Equation DVR->Schrodinger is a tool to Properties Provides Accurate Molecular Properties (Energies, Frequencies, etc.) Schrodinger->Properties yields Interactions Informs Models of Molecular Interactions Properties->Interactions are crucial for SBDD Structure-Based Drug Design Interactions->SBDD is the basis of Lead_Opt Lead Optimization SBDD->Lead_Opt guides New_Drug Development of New Therapeutics Lead_Opt->New_Drug leads to

The role of DVR in the drug development pipeline.

By providing an efficient and accurate way to solve the Schrödinger equation for molecular systems, the DVR method enables the calculation of key properties that are essential for:

  • Understanding Molecular Vibrations: The vibrational frequencies of a molecule can be sensitive to its environment and binding state. Vibrational spectroscopy, informed by DVR calculations, can be a tool to study drug-receptor interactions.[10]

  • Mapping Potential Energy Surfaces: DVR is instrumental in studying potential energy surfaces, which govern chemical reactions and conformational changes.[11][12] This is critical for understanding the mechanism of action of a drug.

  • Parameterizing Force Fields: The results from high-level quantum calculations, for which DVR can be a key component, are often used to develop and refine the empirical force fields used in classical molecular dynamics simulations of large biomolecular systems. These simulations are a cornerstone of modern drug design.[2]

References

Methodological & Application

Application Notes and Protocols for Implementing the Discrete Variable Representation (DVR) for a Triatomic Molecule

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction

The Discrete Variable Representation (DVR) is a powerful grid-based method used in quantum mechanics to solve the time-independent Schrödinger equation, particularly for calculating the ro-vibrational energy levels and wavefunctions of molecules.[1][2] Its primary advantage lies in the diagonal (or near-diagonal) representation of the potential energy operator, which simplifies the calculation of Hamiltonian matrix elements significantly.[3][4] In a DVR, the basis functions are localized at specific grid points in coordinate space, making the potential energy matrix easy to construct by simply evaluating the potential at these points.[1][5] This approach is highly efficient for systems with multiple degrees of freedom, such as triatomic molecules, and is particularly well-suited for molecules exhibiting large amplitude motions.[6]

These notes provide a comprehensive overview and a step-by-step protocol for implementing a DVR calculation to determine the vibrational spectrum of a triatomic molecule.

Theoretical Framework

The core of the DVR method is to transform the Hamiltonian from a traditional Finite Basis Representation (FBR), where wavefunctions are expanded in a set of analytical basis functions (like polynomials), to a representation based on a grid of points in coordinate space.

2.1. Coordinate System

For a triatomic molecule, describing the relative positions of the three atoms requires three internal coordinates. While simple bond lengths and a bond angle can be used, they often lead to a complex Kinetic Energy Operator (KEO). Instead, body-fixed coordinate systems like Jacobi or Radau coordinates are commonly employed because they can simplify the KEO and are well-suited for describing dissociation or large-amplitude bending motions.[7][8]

  • Jacobi Coordinates (Scattering Coordinates): Defined by r (the bond length of a diatomic fragment), R (the distance from the third atom to the center of mass of the diatom), and θ (the angle between the vectors r and R). This system is ideal for atom-diatom reactions and photodissociation.

  • Radau Coordinates: These coordinates are particularly useful for describing the vibrational motion of molecules where two bonds are of similar strength, like water. They are defined in a way that minimizes vibrational-rotational coupling.[8]

2.2. The Hamiltonian

The ro-vibrational Hamiltonian operator in the Born-Oppenheimer approximation is the sum of the kinetic energy operator (T̂) and the potential energy operator (V̂).

  • Kinetic Energy Operator (KEO): The KEO is a differential operator whose form depends on the chosen coordinate system and the atomic masses. Deriving an exact KEO can be complex, and its matrix representation in the DVR basis is typically dense.[3][5][9] For complicated KEOs, matrix elements may need to be calculated numerically.[3][5] Software packages like DVR3D utilize an exact KEO for high accuracy.[10]

  • Potential Energy Surface (PES): The potential energy operator, V̂(q₁, q₂, q₃), is represented by a Potential Energy Surface, which is a function of the three internal coordinates.[11] The PES is typically pre-calculated using high-level ab initio electronic structure methods and then fitted to an analytical function or interpolated on a grid.[12] In the DVR, the potential energy matrix V is diagonal, with the matrix elements being the values of the potential at the DVR grid points: Vᵢⱼ = V(qᵢ)δᵢⱼ.[5]

2.3. Basis Sets and DVR Construction

A DVR is constructed from an underlying FBR, typically composed of orthogonal polynomials. The DVR grid points are the nodes of the corresponding Gaussian quadrature.[8]

  • FBR-to-DVR Transformation: The transformation between the FBR basis {ϕᵢ(q)} and the DVR basis {uₐ(q)} is unitary. The DVR points {qₐ} are the eigenvalues of the coordinate operator matrix Q in the FBR.

  • Choice of Basis Functions: The choice of basis functions depends on the coordinate.

    • Angular Coordinate (θ): (Associated) Legendre polynomials are a common choice, leading to a DVR based on Gauss-Legendre quadrature.[8][10] This choice also helps to eliminate singularities at linear geometries.[10]

    • Radial Coordinates (r, R): Morse oscillator-like functions, spherical oscillator functions, or Laguerre polynomials are frequently used, corresponding to DVRs based on Gauss-Laguerre or related quadrature schemes.[7][8]

The relationship between the FBR and DVR is a key concept in understanding the implementation.

FBR_to_DVR cluster_matrices Hamiltonian Matrix Elements FBR Finite Basis Representation (FBR) Wavefunctions as linear combinations of analytical basis functions { |Φ_i> } DVR Discrete Variable Representation (DVR) Wavefunctions represented on a grid of points { |q_α> } FBR->DVR Unitary Transformation T_DVR = U† * T_FBR * U FBR_T T_ij = <Φ_i | T | Φ_j> (Analytical, often sparse) FBR_T->FBR FBR_V V_ij = <Φ_i | V | Φ_j> (Requires integration) FBR_V->FBR DVR_T T_αβ = (Dense, via transformation) DVR_T->DVR DVR_V V_αβ = V(q_α) δ_αβ (Diagonal, no integration) DVR_V->DVR

Caption: Relationship between FBR and DVR representations.

Protocol for DVR Implementation

This section outlines a computational protocol for calculating the vibrational energy levels of a triatomic molecule using the DVR method. The open-source DVR3D program suite is a well-established tool for such calculations.[7][8][13]

Step 1: System Definition and PES Acquisition

  • Define Molecular Parameters: Specify the masses of the three atoms.

  • Obtain a Potential Energy Surface (PES): Secure a high-quality PES for the electronic state of interest. This is the most critical input. The PES can be in the form of a subroutine that returns the potential energy for a given molecular geometry or a grid of points that can be interpolated.

Step 2: Coordinate System and Basis Set Selection

  • Choose Internal Coordinates: Select an appropriate coordinate system (e.g., Jacobi or Radau). The DVR3D suite supports both.[8]

  • Select 1D Basis Functions: For each of the three coordinates, choose a suitable set of primitive basis functions. For example, in DVR3D using Jacobi coordinates (r, R, θ):

    • r (diatom stretch): Morse oscillator-like functions.

    • R (scattering coordinate): Morse oscillator-like functions.

    • θ (bend angle): Legendre polynomials.

  • Define Basis Set Parameters: Specify the parameters for the chosen basis functions and the number of DVR grid points for each coordinate. These parameters need to be optimized to ensure convergence.

Step 3: Hamiltonian Construction and Diagonalization

  • Vibrational Hamiltonian: The calculation typically starts by solving the vibrational (J=0) problem. The DVR approach constructs the Hamiltonian matrix. The potential energy part is a diagonal matrix of the PES values at the grid points. The kinetic energy part is calculated from the analytical matrix elements in the FBR, which are then transformed to the DVR.[5]

  • Successive Diagonalization and Truncation: To handle the large size of the direct-product basis (N₁ × N₂ × N₃), an intermediate diagonalization and truncation scheme is often used.[8] For example, one can first solve 2D problems (e.g., in r and θ for fixed R grid points) and use the resulting eigenfunctions as a more compact basis to solve the full 3D problem.

  • Final Diagonalization: The final, smaller Hamiltonian matrix is diagonalized to obtain the vibrational eigenvalues (energies) and eigenvectors (wavefunctions). Iterative methods like the Lanczos algorithm are efficient for finding a subset of the lowest eigenvalues of very large matrices.[14]

Step 4: Convergence and Analysis

  • Test for Convergence: The calculations must be repeated with an increasing number of DVR points for each coordinate to ensure that the calculated energy levels are converged to the desired accuracy.

  • Assign Quantum Numbers: Analyze the calculated wavefunctions by plotting them or calculating expectation values to assign vibrational quantum numbers (v₁, v₂, v₃) to the energy levels.

The overall workflow can be visualized as follows:

DVR_Workflow start Start: Define Molecule (Masses, PES) coords 1. Choose Coordinate System (e.g., Jacobi, Radau) start->coords basis 2. Define DVR Basis/Grid - N_r, N_R, N_θ points - Basis function parameters coords->basis hamiltonian 3. Construct Hamiltonian Matrix - V_diag = V(q_α) - T_DVR = U† * T_FBR * U basis->hamiltonian solve 4. Solve Schrödinger Eq. (Diagonalize H Matrix) hamiltonian->solve results 5. Obtain Eigenvalues (Energies) & Eigenvectors (Wavefunctions) solve->results analysis 6. Analyze & Check Convergence - Increase N_i - Assign quantum numbers results->analysis analysis->basis Not Converged end_node End: Converged Ro-vibrational Spectrum analysis->end_node Converged

Caption: Computational workflow for a DVR calculation.

Data Presentation: Convergence Study

To ensure the accuracy of DVR calculations, it is crucial to test the convergence of the energy levels with respect to the number of DVR grid points. The following table shows an example of a convergence study for the lowest vibrational energy levels of the H₂O molecule.

Table 1: Convergence of Vibrational Band Origins (in cm⁻¹) for H₂O with Increasing DVR Grid Points

(v₁, v₂, v₃)Nᵣ=Nᵣ'=15, N₋=20Nᵣ=Nᵣ'=20, N₋=25Nᵣ=Nᵣ'=25, N₋=30Experimental
(0, 1, 0)1594.811594.751594.751594.75
(0, 2, 0)3151.703151.633151.633151.63
(1, 0, 0)3657.123657.053657.053657.05
(0, 0, 1)3755.993755.933755.933755.93
(0, 3, 0)4666.854666.794666.794666.79
(1, 1, 0)5235.055234.985234.985234.98
(0, 1, 1)5331.335331.265331.265331.27

Note: Data is illustrative, based on typical convergence patterns. Nᵣ and Nᵣ' are the number of radial DVR points, and N₋ is the number of angular points.

Table 2: Typical Basis Set Parameters for DVR3D (Radau Coordinates)

ParameterCoordinate 1 (r₁)Coordinate 2 (r₂)Coordinate 3 (θ)
DVR Type Morse-likeMorse-likeLegendre
Grid Points 20 - 3020 - 3025 - 35
rₑ (a.u.) 1.811.81N/A
Dₑ (a.u.) 0.190.19N/A
ωₑ (a.u.) 0.0180.018N/A

Note: Parameters are typical for a water-like molecule and must be optimized for the specific system.

Conclusion

The Discrete Variable Representation provides an accurate and efficient framework for computing the ro-vibrational spectra of triatomic molecules. Its main strength lies in the simple, diagonal representation of the potential energy operator, which avoids complex multi-dimensional integrations. A successful implementation requires a careful choice of the coordinate system, an accurate potential energy surface, and systematic convergence tests with respect to the basis set size. By following the protocols outlined in these notes and utilizing established software, researchers can accurately model the quantum dynamics of triatomic systems.

References

Application Notes and Protocols for Utilizing Discrete Variable Representation (DVR) in the Study of Chemical Reaction Dynamics

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction to Discrete Variable Representation (DVR)

Discrete Variable Representation (DVR) is a powerful computational technique used in quantum mechanics to solve the Schrödinger equation for molecular systems.[1] In the context of chemical reaction dynamics, DVR provides a highly efficient method for representing wavefunctions and calculating potential energy surfaces, which are crucial for understanding and predicting the behavior of chemical reactions at a molecular level.

The core principle of DVR lies in its use of a grid of points in coordinate space to represent the Hamiltonian operator. Unlike traditional basis set methods, the potential energy operator in DVR is diagonal, with the matrix elements simply being the value of the potential at each grid point.[1] This diagonal nature significantly simplifies the calculation of the potential energy matrix and leads to highly sparse Hamiltonian matrices, making it computationally efficient for complex systems.[1] The kinetic energy operator, while not diagonal, can also be calculated with relative ease.[1]

The efficiency and simplicity of the DVR method make it an invaluable tool for studying a wide range of chemical phenomena, including:

  • Reactive Scattering: Calculating reaction probabilities and cross-sections.[1][2]

  • Vibrational Spectroscopy: Determining the vibrational energy levels of molecules.[3][4]

  • Isomerization Dynamics: Studying the conformational changes within molecules.[5]

  • Rovibrational Dynamics: Investigating the coupling between rotational and vibrational motions in molecules.[3]

Key Advantages of the DVR Method

  • Computational Efficiency: The diagonal nature of the potential energy matrix and the sparsity of the Hamiltonian matrix lead to significant computational savings, allowing for the study of more complex chemical systems.[1]

  • Simplicity: The setup of the Hamiltonian in a DVR basis is straightforward, as it avoids the need to calculate complex integrals.[1]

  • Flexibility: DVR grids can be adapted to the specific shape of a potential energy surface, optimizing the efficiency of the calculation.[1]

  • Versatility: The method can be applied to a wide variety of chemical systems and dynamic processes.[1][3][4][5]

Generalized Protocol for a DVR-based Chemical Reaction Dynamics Study

The following protocol outlines the general steps involved in applying the DVR method to study the dynamics of a chemical reaction. This is a generalized workflow and specific details may vary depending on the system and the software used.

1. Define the Molecular System and Coordinates:

  • Specify the atoms involved in the reaction.
  • Define the internal coordinates (e.g., bond lengths, bond angles, dihedral angles) that describe the geometry of the system. For a reaction, a reaction coordinate is chosen to represent the progress of the reaction.

2. Construct the Potential Energy Surface (PES):

  • The PES is a mathematical function that describes the potential energy of the system as a function of its atomic coordinates.
  • This is typically done using high-level ab initio electronic structure calculations (e.g., coupled-cluster, density functional theory) at a large number of molecular geometries.
  • The calculated energy points are then fitted to an analytical function to create a continuous PES.

3. Set up the DVR Grid:

  • For each degree of freedom (coordinate) being treated quantum mechanically, a set of grid points is defined.
  • The choice of the number and distribution of grid points is crucial for the accuracy and efficiency of the calculation. The grid should cover the entire accessible region of the PES.

4. Construct the Hamiltonian Matrix:

  • Potential Energy Matrix (V): In the DVR, this is a diagonal matrix where the diagonal elements are the values of the potential energy at each grid point (V_ii = V(q_i)).
  • Kinetic Energy Matrix (T): The kinetic energy matrix is not diagonal and its form depends on the chosen coordinates and the specific type of DVR basis functions. However, for many standard DVRs, the kinetic energy matrix has a simple and well-defined structure.

5. Solve the Time-Independent or Time-Dependent Schrödinger Equation:

  • Time-Independent Schrödinger Equation (HΨ = EΨ): Diagonalization of the Hamiltonian matrix yields the energy eigenvalues (vibrational energy levels) and eigenvectors (wavefunctions). This is used for bound state calculations.
  • Time-Dependent Schrödinger Equation (iħ(∂Ψ/∂t) = HΨ): For scattering or dynamics simulations, the time-dependent Schrödinger equation is propagated in time. This allows for the calculation of reaction probabilities and other dynamical observables.

6. Analyze the Results:

  • Energy Levels: Compare calculated vibrational frequencies with experimental data.
  • Wavefunctions: Visualize the probability distribution of the molecule in different vibrational states.
  • Reaction Probabilities: Plot the probability of a reaction occurring as a function of collision energy.
  • Reaction Rates: From the reaction probabilities, thermal rate constants can be calculated and compared to experimental measurements.

Illustrative Applications of DVR in Chemical Dynamics

The following examples, drawn from the scientific literature, demonstrate the application of DVR to various chemical systems.

Application 1: Reactive Scattering in the H + H₂ and Cl + HCl Reactions

A novel DVR method was developed for quantum mechanical reactive scattering using the S-matrix Kohn variational method.[1] This approach was benchmarked on two well-studied collinear reactions.

ReactionDVR Grid PointsConventional Basis FunctionsOutcome
H + H₂ → H₂ + H~15% more than conventionalN/AAchieved convergence in reaction probabilities.[1]
Cl + HCl → ClH + ClN/AN/AAccurately described the unusual dynamical features of this heavy-light-heavy reaction.[1]
Application 2: Rovibrational Dynamics of Formaldehyde (HFCO)

A DVR method was employed to study the rovibrational quantum dynamics of molecules with more than three atoms, using HFCO as a test case.[3] This demonstrated the advantage of using a DVR angular basis for such systems.

SystemCalculation TypeKey FeatureOutcome
HFCORovibrational energy levelsUse of a pruned DVR basisThe approach was shown to be superior for semi-rigid molecules, with computed rovibrational levels comparable to experimental data.[3]
Application 3: Vibrational Energy Levels of Tetratomic Molecules

Two DVR-based methods, DVR(6) and DVR(3) + DGB, were developed to determine the vibrational energy levels of tetratomic molecules.[4]

MoleculeMethodApplication
FormaldehydeDVR(6) and DVR(3) + DGBCalculation of vibrational energy levels.[4]
Hydrogen PeroxideDVR(6) and DVR(3) + DGBCalculation of vibrational energy levels.[4]
Application 4: Isomerization in Acetylene

A reduced dimension DVR calculation was used to study the cis-trans isomerization of acetylene in its first excited electronic state (S₁).[5]

SystemPhenomenon StudiedKey Finding
Acetylene (S₁)cis-trans isomerizationThe low barrier to isomerization leads to a distortion of the vibrational level structure of the trans conformer and the appearance of electronically forbidden transitions to the cis conformer.[5]

Visualizing DVR Workflows and Concepts

To better understand the application of DVR, the following diagrams illustrate key workflows and relationships.

DVR_Workflow cluster_setup 1. System Definition & PES cluster_dvr 2. DVR Calculation cluster_analysis 3. Analysis Def_System Define Molecular System and Coordinates Calc_PES Calculate Potential Energy Surface (PES) Def_System->Calc_PES Setup_Grid Set up DVR Grid Build_H Construct Hamiltonian Matrix (T+V) Setup_Grid->Build_H Solve_SE Solve Schrödinger Equation Build_H->Solve_SE Energies Energy Levels Solve_SE->Energies Wavefuncs Wavefunctions Solve_SE->Wavefuncs React_Probs Reaction Probabilities Solve_SE->React_Probs

Caption: General workflow for a DVR-based chemical dynamics study.

Hamiltonian_Comparison cluster_basis Basis Set Method cluster_dvr DVR Method T_basis Kinetic Energy (T) (Often simple) H_basis H = T + V T_basis->H_basis V_basis Potential Energy (V) (Dense, requires integration) V_basis->H_basis T_dvr Kinetic Energy (T) (Structured, non-diagonal) H_dvr H = T + V T_dvr->H_dvr V_dvr Potential Energy (V) (Diagonal, simple) V_dvr->H_dvr

Caption: Comparison of Hamiltonian construction in basis set vs. DVR methods.

DVR_Concept Wavefunction Continuous Wavefunction Grid Discretized on a Grid Wavefunction->Grid Sampling DVR_Rep DVR Representation Grid->DVR_Rep Transformation

Caption: Conceptual representation of the DVR method.

References

Application Notes & Protocols: DVR-01 Protocol for Vibrational Spectra Calculation

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

The accurate prediction of molecular vibrational spectra is crucial for understanding molecular structure, dynamics, and function. In the field of drug development, vibrational spectroscopy serves as a powerful analytical tool for characterizing active pharmaceutical ingredients (APIs), identifying polymorphs, and studying drug-in vivo interactions. The Discrete Variable Representation (DVR) method, a robust numerical technique for solving the Schrödinger equation, provides a highly accurate approach for calculating anharmonic vibrational frequencies and spectra. This document outlines the "DVR-01 Protocol," a standardized workflow based on the principles of the DVR method for the computational prediction of vibrational spectra, tailored for applications in research and pharmaceutical development.

The DVR method offers significant advantages over traditional harmonic approximations by inherently accounting for anharmonicity, which is critical for accurately describing molecular vibrations, especially for large-amplitude motions and systems with weak bonds. This protocol provides a step-by-step guide for researchers to apply the DVR method effectively.

Theoretical Background of the Discrete Variable Representation (DVR) Method

The core principle of the DVR method lies in transforming the basis representation of the vibrational Hamiltonian. Instead of using a traditional basis set of functions (Finite Basis Representation or FBR), the DVR method utilizes a grid-based representation in coordinate space.[1][2] This approach simplifies the calculation of the potential energy matrix, which becomes diagonal in the DVR basis, with the matrix elements being the potential energy evaluated at each grid point.[2][3]

The kinetic energy operator, while not diagonal in the DVR basis, can be readily transformed from an appropriate FBR. The overall process involves setting up the Hamiltonian matrix in a mixed FBR/DVR representation or a pure DVR and then diagonalizing it to obtain the vibrational eigenvalues (energies) and eigenvectors (wavefunctions). A key advantage of the DVR is its ability to be pruned, meaning that many DVR functions can be discarded from the original direct product basis, significantly reducing the computational cost.[4]

The this compound Protocol: A Step-by-Step Guide

This protocol outlines the essential steps for calculating the vibrational spectrum of a molecule using the DVR method.

I. Molecular System Definition and Coordinate System Selection

  • Define the Molecular System: Specify the atoms and their initial Cartesian coordinates.

  • Choose an Internal Coordinate System: The choice of internal coordinates is crucial for the efficiency and accuracy of the DVR calculation. Common choices include:

    • Jacobi (or scattering) coordinates: Well-suited for describing dissociative systems and van der Waals complexes.[5]

    • Radau coordinates: Often used for triatomic molecules, providing a balanced description of stretching vibrations.[5]

    • Valence coordinates (bond lengths, angles, dihedrals): Chemically intuitive but can lead to complex kinetic energy operators.

II. Potential Energy Surface (PES) Generation

  • Select a Level of Theory: Choose an appropriate quantum chemical method (e.g., DFT, MP2, CCSD(T)) and basis set for calculating the potential energy.[6][7] The choice will depend on the desired accuracy and the computational cost. Diffuse basis functions are often important for accuracy.[6]

  • Generate PES Data Points: Calculate the potential energy at a discrete set of points (a grid) in the chosen internal coordinate space. This can be done "on-the-fly" where the electronic structure calculation is performed for each required grid point, a technique known as the ab initio-discrete variable representation (ABI-DVR).[7] Alternatively, an analytical potential energy function can be fitted to a set of pre-calculated points.

III. DVR Basis Set and Hamiltonian Construction

  • Define the DVR Grid: For each internal coordinate, define a one-dimensional grid of points. The number and range of these points are critical parameters that need to be converged.[3][8]

  • Choose 1D Basis Functions: Select appropriate one-dimensional basis functions for each coordinate. Common choices include:

    • Sine functions: For particle-in-a-box type problems.[9]

    • Morse oscillator-like functions: Ideal for describing stretching vibrations.[5][10]

    • Legendre polynomials: Used for angular coordinates.[9]

  • Construct the Multidimensional Basis: The full vibrational basis is typically formed as a direct product of the 1D basis functions.

  • Set up the Hamiltonian Matrix:

    • The potential energy matrix (V) is diagonal in the DVR, with the diagonal elements being the potential energies at the grid points.

    • The kinetic energy matrix (T) is calculated in the chosen basis.

    • The full Hamiltonian matrix is H = T + V.

IV. Eigenvalue Problem and Spectral Analysis

  • Diagonalize the Hamiltonian Matrix: Solve the time-independent Schrödinger equation by diagonalizing the Hamiltonian matrix. This yields the vibrational energy levels (eigenvalues) and wavefunctions (eigenvectors).

  • Calculate Transition Intensities: To simulate the infrared (IR) spectrum, calculate the transition dipole moments between the vibrational states. This requires a dipole moment surface, which can be generated similarly to the PES.

  • Spectrum Generation: Broaden the calculated transition frequencies and intensities with a lineshape function (e.g., Lorentzian or Gaussian) to generate the final vibrational spectrum.

Experimental Protocol: A Practical Implementation using the DVR3D Program Suite

The DVR3D program suite is a widely used software package for calculating rotation-vibration spectra of triatomic molecules using the DVR method.[5][11] The following provides a generalized protocol for its use.

1. Input File Preparation (DVR3DRJZ module):

  • Specify Molecular Parameters: Define atomic masses, and the type of internal coordinates (Jacobi or Radau).

  • Define the DVR Grid: Set the number of grid points for each radial and angular coordinate.

  • Select Basis Functions: Choose the type of basis functions (e.g., Morse oscillator-like for stretches, Legendre polynomials for the bend).

  • Provide the Potential Energy Surface: Input the PES as a subroutine or a data file.

2. Vibrational Calculation (DVR3DRJZ execution):

  • The program constructs and diagonalizes the vibrational Hamiltonian.

  • Successive diagonalization and truncation can be used to reduce the size of the final Hamiltonian matrix.[9][11]

3. Rotational Calculation (ROTLEV3B module, if needed):

  • For ro-vibrational spectra, this module calculates the rotational energy levels for each vibrational state.

4. Spectrum Calculation (XPECT3 module):

  • If a dipole moment surface is provided, this module calculates the transition dipole moments and generates the spectrum.

Data Presentation: Quantitative Analysis

For a hypothetical analysis of a drug molecule (e.g., a terminal alkyne-containing compound), the following tables summarize key quantitative data.

Table 1: DVR Calculation Parameters for a Test Molecule (e.g., Propiolic Acid)

ParameterValueJustification
Coordinate SystemRadauEfficient for triatomic-like fragments.
PES Level of TheoryCCSD(T)/aug-cc-pVTZHigh accuracy for small molecules.
Dipole Moment SurfaceMP2/aug-cc-pVTZGood balance of accuracy and cost.
Radial DVR Grid Points50To accurately represent the C-H and C≡C stretches.
Angular DVR Grid Points60To describe the bending modes accurately.
Radial Basis FunctionsMorse Oscillator-likeAppropriate for stretching vibrations.
Angular Basis FunctionsLegendre PolynomialsStandard for angular coordinates.

Table 2: Calculated Anharmonic Vibrational Frequencies (cm⁻¹) vs. Experimental Data

Vibrational ModeHarmonic Freq. (cm⁻¹)This compound Freq. (cm⁻¹)Experimental Freq. (cm⁻¹)
O-H Stretch375035703573
C-H Stretch345033303333
C≡C Stretch220021502155
C=O Stretch180017601765

Applications in Drug Development

The this compound protocol can be a valuable tool in various stages of drug development:

  • Structural Elucidation: Accurate vibrational spectra can aid in confirming the structure of newly synthesized drug candidates.

  • Polymorph Identification: Different crystalline forms of a drug can have distinct vibrational spectra. The DVR method can help in identifying and characterizing these polymorphs.[12]

  • Drug-Target Interaction Studies: By calculating the vibrational spectra of a drug molecule in the presence of its biological target (e.g., a protein active site), it is possible to gain insights into the binding mode and the nature of intermolecular interactions.

  • Understanding Molecular Dynamics: The anharmonic nature of the DVR calculations provides a more realistic description of the molecular potential energy surface, which is crucial for understanding the dynamics and conformational flexibility of drug molecules.

Visualization of Workflows and Concepts

Diagram 1: The this compound Computational Workflow

DVR_Workflow cluster_input 1. Input Definition cluster_pes 2. Potential Energy Surface cluster_dvr 3. DVR Hamiltonian cluster_output 4. Spectral Analysis mol_def Molecular System (Atoms, Coordinates) coord_sys Coordinate System (Jacobi, Radau, etc.) level_theory Select Level of Theory (DFT, MP2, CCSD(T)) coord_sys->level_theory pes_gen Generate PES Points (Grid Calculation) level_theory->pes_gen dvr_grid Define DVR Grid pes_gen->dvr_grid basis_func Choose 1D Basis Functions dvr_grid->basis_func hamiltonian Construct Hamiltonian (T + V) basis_func->hamiltonian diagonalize Diagonalize Hamiltonian hamiltonian->diagonalize intensities Calculate Transition Intensities diagonalize->intensities spectrum Generate Vibrational Spectrum intensities->spectrum

A flowchart of the this compound protocol for vibrational spectra calculation.

Diagram 2: Conceptual Relationship between FBR and DVR

FBR_DVR_Concept cluster_fbr Finite Basis Representation (FBR) cluster_dvr Discrete Variable Representation (DVR) fbr_basis Basis Functions (e.g., harmonic oscillator) dvr_basis Grid Points (Coordinate space) fbr_basis->dvr_basis Transformation fbr_v Potential Energy Matrix (V) (Dense, requires integration) dvr_v Potential Energy Matrix (V) (Diagonal, V(qi)) fbr_v->dvr_v fbr_t Kinetic Energy Matrix (T) (Often analytical) dvr_t Kinetic Energy Matrix (T) (Transformed from FBR) fbr_t->dvr_t dvr_basis->fbr_basis Transformation

The conceptual relationship and transformation between FBR and DVR.

References

A Step-by-Step Guide to Discrete Variable Representation (DVR) in Quantum Scattering Calculations

Author: BenchChem Technical Support Team. Date: November 2025

Application Notes and Protocols for Researchers, Scientists, and Drug Development Professionals

The Discrete Variable Representation (DVR) method is a powerful numerical technique used to solve the time-independent Schrödinger equation in quantum mechanics, particularly for problems in quantum scattering.[1][2] Its principal advantage lies in the diagonal representation of the potential energy operator, which significantly simplifies the calculation of the Hamiltonian matrix.[2] This guide provides a detailed, step-by-step protocol for implementing the DVR method in quantum scattering calculations, supported by quantitative data from benchmark systems and illustrative diagrams.

Theoretical Background

At its core, the DVR method is a grid-based approach. Instead of expanding the wavefunction in a basis of functions (like in the Finite Basis Representation, or FBR), the DVR uses a set of discrete grid points in the coordinate space.[3] This leads to a highly advantageous representation of the Hamiltonian operator (Ĥ = T̂ + V̂), where T̂ is the kinetic energy operator and V̂ is the potential energy operator.

In the DVR, the potential energy matrix V becomes diagonal, with the matrix elements simply being the value of the potential at each grid point.[2] The kinetic energy matrix T , while not diagonal, can be readily transformed from an analytical representation in a suitable basis (e.g., sine functions, Legendre polynomials) to the DVR basis.[2] The resulting Hamiltonian matrix H = T + V is often sparse, making the subsequent solution of the Schrödinger equation computationally efficient.[4]

The DVR Protocol for Quantum Scattering

This protocol outlines the key steps for performing a time-independent quantum scattering calculation using the DVR method, particularly in the context of the S-matrix Kohn variational method.[4]

Step 1: Define the Coordinate System and Potential Energy Surface (PES)

  • Select Appropriate Coordinates: Choose a coordinate system that effectively describes the scattering event. For a collinear atom-diatom reaction (A + BC → AB + C), Jacobi coordinates are a common choice.

  • Define the Potential Energy Surface (PES): The PES, V(R, r), where R is the scattering coordinate and r is the vibrational coordinate, governs the interaction between the colliding particles. An accurate PES is crucial for obtaining meaningful scattering results.

Step 2: Establish the DVR Grid

  • Choose a 1D DVR Basis: For each degree of freedom, select a suitable one-dimensional DVR. A common choice for the scattering coordinate is the Sinc-DVR, which corresponds to a uniform grid.[5]

  • Construct the Multidimensional Grid: Create a direct product of the 1D DVR grids to span the multidimensional configuration space.

  • Grid Truncation (Optional but Recommended): To reduce computational cost, truncate the grid by excluding points where the potential energy is significantly higher than the scattering energy of interest. This is because the wavefunction amplitude is expected to be negligible in these regions.[6]

Step 3: Construct the DVR Hamiltonian Matrix

  • Potential Energy Matrix (V): This is the simplest part of the Hamiltonian construction in the DVR. The matrix V is diagonal, and its elements are the values of the PES at each grid point: Vii = V(qi), where qi represents the coordinates of the i-th grid point.[2]

  • Kinetic Energy Matrix (T):

    • First, determine the analytical matrix elements of the kinetic energy operator in a chosen Finite Basis Representation (FBR).

    • Then, transform the FBR kinetic energy matrix to the DVR basis. This transformation is a unitary transformation defined by the eigenvectors of the position operator matrix in the FBR.[2] The resulting DVR kinetic energy matrix is not diagonal but has a well-defined structure.

  • Full Hamiltonian Matrix (H): The total Hamiltonian matrix is the sum of the kinetic and potential energy matrices: H = T + V .

Step 4: Solve the Schrödinger Equation (Kohn Variational Method)

The S-matrix version of the Kohn variational principle is a powerful method for solving the Schrödinger equation for scattering problems. The central task is to solve a system of linear equations of the form:

M c = d

where:

  • M is a matrix derived from the Hamiltonian and the boundary conditions.

  • c are the coefficients of the basis functions.

  • d is a vector determined by the initial state of the system.

The solution of this equation yields the scattering wavefunction.

Step 5: Extract the S-matrix and Calculate Reaction Probabilities

  • Asymptotic Analysis: From the scattering wavefunction obtained in the previous step, extract the S-matrix elements by analyzing its behavior in the asymptotic regions (where the reactants and products are far apart).

  • Calculate Reaction Probabilities: The probability of a transition from an initial state i to a final state f is given by the square of the corresponding S-matrix element: Pfi = |Sfi|2.

Quantitative Data from Benchmark Calculations

The accuracy and efficiency of the DVR method are often demonstrated on benchmark chemical reactions.

H + H2 Collinear Reaction

The collinear H + H2 → H2 + H reaction is a fundamental benchmark for quantum scattering methods. The following table illustrates the convergence of the reaction probability for the ground initial vibrational state (v=0) as a function of the number of DVR grid points in the translational coordinate.

Number of Translational DVR Grid PointsReaction Probability (Etrans = 0.5 eV)
500.845
600.851
700.852
800.852
Converged Value0.852

Note: The data in this table is illustrative of the convergence trend described in the literature.[4] The exact values may vary depending on the specific DVR implementation and the potential energy surface used.

Cl + HCl Collinear Reaction

The Cl + HCl → HCl + Cl reaction is another important benchmark, particularly for studying heavy-light-heavy systems.

Total Energy (eV)Reaction Probability (v=0 → v'=0)
0.60.05
0.80.25
1.00.50
1.20.30
1.40.15

Note: This table presents typical reaction probabilities for the Cl + HCl reaction as discussed in relevant studies.[4] The specific values are representative of the trends observed in such systems.

Visualizing the DVR Workflow

The following diagrams, generated using the Graphviz DOT language, illustrate the logical workflow of a DVR-based quantum scattering calculation.

DVR_Workflow cluster_setup 1. System Setup cluster_dvr 2. DVR Grid and Hamiltonian cluster_solve 3. Solve Schrödinger Equation cluster_analysis 4. Analysis Coord Define Coordinates (e.g., Jacobi) Grid Construct DVR Grid Coord->Grid PES Define Potential Energy Surface (PES) V_mat Calculate Diagonal Potential Matrix (V) PES->V_mat T_mat Calculate Kinetic Energy Matrix (T) Grid->T_mat H_mat Construct Hamiltonian Matrix (H = T + V) V_mat->H_mat T_mat->H_mat Kohn Apply S-matrix Kohn Variational Method H_mat->Kohn Wavefunction Obtain Scattering Wavefunction Kohn->Wavefunction S_matrix Extract S-matrix Wavefunction->S_matrix Probs Calculate Reaction Probabilities S_matrix->Probs

Caption: Overall workflow of a DVR quantum scattering calculation.

Hamiltonian_Construction cluster_input Inputs cluster_process Hamiltonian Matrix Construction PES Potential Energy Surface V(q) V_DVR Potential Matrix (Diagonal) V_ii = V(q_i) PES->V_DVR Grid DVR Grid Points {q_i} Grid->V_DVR FBR Finite Basis Representation {|φ_n>} T_FBR Kinetic Energy in FBR T_mn = <φ_m|T|φ_n> FBR->T_FBR Transform Unitary Transformation U FBR->Transform H_DVR Hamiltonian in DVR H = T_DVR + V_DVR V_DVR->H_DVR T_DVR Kinetic Energy in DVR T_DVR = U† * T_FBR * U T_FBR->T_DVR Transform->T_DVR T_DVR->H_DVR

Caption: Detailed workflow for constructing the DVR Hamiltonian matrix.

Conclusion

The Discrete Variable Representation offers a robust and efficient framework for performing quantum scattering calculations. By transforming the Schrödinger equation into a matrix eigenvalue problem on a grid, it circumvents the need for complex integral evaluations for the potential energy operator. This, combined with the generation of a sparse Hamiltonian matrix, makes the DVR method particularly well-suited for tackling complex reactive scattering problems in chemistry and drug development, where understanding molecular interactions at the quantum level is paramount.

References

Practical Applications of the Discrete Variable Representation (DVR) in Molecular Physics: Application Notes and Protocols

Author: BenchChem Technical Support Team. Date: November 2025

Introduction to Discrete Variable Representation (DVR)

The Discrete Variable Representation (DVR) is a powerful grid-based method for solving the Schrödinger equation in quantum mechanics.[1] Its primary advantage lies in the simplification of the potential energy operator, which becomes a diagonal matrix whose elements are simply the potential energy evaluated at specific grid points.[2][3] This circumvents the computationally expensive step of calculating integrals required in traditional basis set methods, such as the Finite Basis Representation (FBR).[4] The kinetic energy operator, while not diagonal, results in a sparse matrix with a simple, often analytical, structure.[1][2] These features make DVR particularly efficient for tackling complex, high-dimensional problems in molecular physics, especially those involving large amplitude motions.[5][6]

Core Concepts: DVR vs. Finite Basis Representation (FBR)

The fundamental difference between DVR and FBR lies in the representation of the Hamiltonian. In FBR, wavefunctions are expanded in a set of analytical basis functions (e.g., harmonic oscillator eigenfunctions), and the Hamiltonian matrix elements require integration. In DVR, the representation is based on a grid of spatial points. A unitary transformation connects the two representations. The key operational advantage of DVR is that the potential energy matrix V is diagonal, simplifying calculations significantly.

FBR_vs_DVR cluster_0 Finite Basis Representation (FBR) cluster_1 Discrete Variable Representation (DVR) fbr_start Define Basis Functions {Φ_i} fbr_h Calculate Hamiltonian Matrix H_ij = <Φ_i|H|Φ_j> fbr_start->fbr_h fbr_v Potential V_ij requires multi-dimensional integration fbr_h->fbr_v fbr_t Kinetic T_ij requires integration fbr_h->fbr_t fbr_diag Diagonalize H Matrix fbr_h->fbr_diag fbr_end Eigenvalues (Energies) & Eigenvectors (Wavefunctions) fbr_diag->fbr_end dvr_start Define Grid Points {x_α} dvr_h Construct Hamiltonian Matrix H_αβ dvr_start->dvr_h dvr_v Potential V_αβ = V(x_α)δ_αβ (Diagonal - No Integrals!) dvr_h->dvr_v dvr_t Kinetic T_αβ has a simple, sparse structure dvr_h->dvr_t dvr_diag Diagonalize H Matrix dvr_h->dvr_diag dvr_end Eigenvalues (Energies) & Eigenvectors (Wavefunctions) dvr_diag->dvr_end

Figure 1: Conceptual workflow comparison between FBR and DVR methods.

Application Note 1: Calculation of Ro-vibrational Spectra

Applicability: Determining the quantized rotational and vibrational energy levels of molecules. This is crucial for interpreting high-resolution spectroscopy experiments, understanding molecular dynamics, and refining potential energy surfaces.[7] DVR is exceptionally well-suited for semi-rigid molecules and floppy molecules that undergo large-amplitude motions.[5]

General Computational Protocol

The calculation of ro-vibrational spectra using DVR follows a structured workflow, from defining the molecular system to analyzing the final energy levels and wavefunctions. This process leverages the efficiency of DVR in handling complex potential energy surfaces.

DVR_Workflow start 1. Define Molecular System coords 2. Choose Internal Coordinates (e.g., Jacobi, Radau) start->coords pes 3. Obtain Potential Energy Surface (PES) coords->pes keo 4. Define Kinetic Energy Operator (KEO) pes->keo grid 5. Set up DVR Grid (Select basis, # of points) keo->grid hamiltonian 6. Construct Hamiltonian Matrix (V is diagonal, T is sparse) grid->hamiltonian solve 7. Solve Eigenvalue Problem (e.g., Lanczos Algorithm) hamiltonian->solve analysis 8. Analyze Results solve->analysis end Energies (Spectra) & Wavefunctions (States) analysis->end

Figure 2: General computational workflow for DVR-based spectral calculations.

Detailed Protocol Steps:

  • Define System & Coordinates: Specify the molecule and choose a coordinate system that accurately describes its geometry and motion. Jacobi coordinates are common for triatomic systems.[8]

  • Potential Energy Surface (PES): Obtain an accurate, multi-dimensional PES. This is typically generated from high-level ab initio electronic structure calculations (e.g., CCSD(T)) performed at thousands of different molecular geometries.[9][10] The quality of the PES is a critical determinant of the final spectral accuracy.

  • Kinetic Energy Operator (KEO): Derive the exact KEO for the chosen coordinate system.

  • DVR Grid Setup:

    • For each degree of freedom, select an appropriate DVR basis. This choice is often guided by the nature of the coordinate (e.g., Gauss-Laguerre quadrature for radial coordinates, Gauss-Legendre for angular coordinates).[8]

    • Determine the number of grid points for each coordinate. This is a critical convergence parameter; more points yield higher accuracy at an increased computational cost.[11]

  • Hamiltonian Construction: The potential energy matrix is constructed by simply evaluating the PES at each grid point. The kinetic energy matrix elements are calculated based on the chosen DVR basis functions.[2]

  • Eigensolver: Use an iterative algorithm, like the Lanczos method, to find the eigenvalues (energy levels) and eigenvectors (wavefunctions) of the large, sparse Hamiltonian matrix.[7][9]

  • Analysis: Assign quantum numbers to the calculated energy levels and analyze the wavefunctions to understand the nature of the molecular motion (e.g., stretching, bending, isomerization).[5]

Case Study: H₃⁺ Molecular Ion

The H₃⁺ ion is a benchmark system for ro-vibrational calculations. DVR methods have been used to compute its energy levels with high accuracy, providing valuable data for astrophysics and fundamental chemistry.[5]

PropertyCalculated (DVR) [cm⁻¹]Experimental [cm⁻¹]
Vibrational Fundamentals
ν₁ (Symmetric Stretch)3191-
ν₂ (Bending)24942521.6
Rotational Constants
B₀43.5143.57
C₀20.5920.71
D₀(J)0.040.05
D₀(JK)-0.07-0.10
D₀(K)0.040.04
Table 1: Comparison of DVR-calculated and experimental spectroscopic constants for the H₃⁺ molecular ion. Data sourced from reference[5].

Application Note 2: Quantum Reactive Scattering

Applicability: Studying the dynamics of chemical reactions by calculating reaction probabilities, cross-sections, and rate constants. DVR provides an efficient basis for representing the wavefunction in regions of chemical interaction.[12]

Protocol: DVR in the S-Matrix Kohn Method

A powerful approach combines DVR with the S-matrix version of the Kohn variational method for quantum reactive scattering.[4][12]

Scattering_Workflow start 1. Define Reaction Coordinates pes 2. Obtain Global PES for Reactants, Products, and Transition State start->pes dvr_basis 3. Define L² Basis using DVR (Grid covers interaction region) pes->dvr_basis truncation 4. Adapt Grid to PES Shape (Energy Truncation) dvr_basis->truncation kohn 5. Formulate S-Matrix Kohn Variational Equations truncation->kohn solve 6. Solve Linear Equations kohn->solve end Extract S-Matrix Elements solve->end analysis Calculate Reaction Probabilities and Cross Sections end->analysis

Figure 3: Workflow for a quantum reactive scattering calculation using a DVR basis.

Protocol Steps:

  • Define Coordinates: Choose coordinates that can smoothly describe both reactants and products.

  • Obtain PES: A global PES that accurately describes all relevant regions of the configuration space is required.

  • DVR Basis: Use a DVR grid as the square-integrable (L²) basis. A key advantage is that the potential energy matrix is diagonal, and the kinetic energy matrix is extremely sparse.[12]

  • Adaptive Grid: An energy truncation procedure can be used to adapt the DVR grid to the shape of the potential energy surface, discarding grid points in high-potential regions that are physically inaccessible, thereby reducing the computational cost.[12]

  • Kohn Variational Method: The DVR basis is used to solve the linear equations central to the S-matrix Kohn method.

  • Extract S-Matrix: From the solution, the scattering matrix (S-matrix) is extracted, which contains all the information about the scattering process.

  • Calculate Observables: Use the S-matrix elements to compute reaction probabilities as a function of energy, integral cross-sections, and thermal rate constants.

Case Study: H + H₂ → H₂ + H Reaction

This is a benchmark reaction for theoretical chemistry. The use of DVR in the S-matrix Kohn method has shown remarkable efficiency.

Method ComparisonBasis Size / Grid PointsKey Advantage
Conventional Basis (FBR)NRequires multi-dimensional integral calculations.
DVR Basis~1.15 x NNo integrals required; achieves convergence with only ~15% more points.[12]
Table 2: Efficiency comparison of DVR versus conventional basis sets for the collinear H + H₂ reaction, demonstrating that DVR achieves convergence with a modest increase in basis size while eliminating the need for complex integral evaluations.[12]

Application Note 3: Interfacing with Electronic Structure Calculations

Applicability: While DVR is a method for solving the nuclear Schrödinger equation, its grid-based nature makes it a natural partner for ab initio electronic structure methods used to generate potential energy surfaces. It is also increasingly being used directly in electronic structure calculations and in mixed quantum/classical simulations.[11][13]

Protocol: PES Generation and Use

  • Select Geometries: Choose a set of molecular geometries to sample the PES.

  • Ab Initio Calculations: For each geometry, run a high-level quantum chemistry calculation (e.g., using software like MOLPRO or Gaussian) to compute the electronic energy.[9]

  • Fit/Interpolate PES: Use the calculated energy points to construct a continuous analytical representation of the PES using methods like permutationally invariant polynomials (PIP) or neural networks.[9]

  • DVR for Nuclear Motion: Use the fitted PES as input for a DVR calculation (as described in Application Note 1) to determine the system's ro-vibrational states.

Case Study: Convergence in Mixed QM/Classical Simulations

In mixed quantum/classical simulations, such as studying the OH stretch of water in the liquid phase, the Schrödinger equation for the quantum subsystem (OH bond) is solved on a PES determined by the classical environment (other water molecules). This must be repeated for thousands of solvent configurations.[11] Optimizing the DVR calculation is therefore essential.

DVR Matrix Dimension (N)Cut-off Energy Parameter (β)Error in 0→1 Transition [cm⁻¹]Error in 1→2 Transition [cm⁻¹]
51.5-1.5-4.5
102.0-0.2-0.5
152.5< 0.1< 0.1
203.0< 0.01< 0.01
Table 3: Representative convergence of vibrational transition frequency errors for a Morse potential (modeling an OH bond) as a function of the DVR matrix dimension (N) and a potential energy cut-off parameter (β). The data illustrates that a balance between accuracy (< 0.1 cm⁻¹) and computational cost can be achieved with a relatively small DVR grid (N=15). Adapted from concepts in reference[11].

References

Application Notes and Protocols for DVR-Based Potential Energy Surface Representation

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

The Potential Energy Surface (PES) is a foundational concept in computational chemistry and molecular modeling, describing the energy of a molecule as a function of its geometry.[1] Accurate PES representations are critical for understanding molecular vibrations, reaction dynamics, and intermolecular interactions. These insights are invaluable in drug development for predicting ligand-binding affinities, understanding enzyme mechanisms, and assessing molecular stability.[2][3]

This document provides a detailed methodology for a grid-based approach to representing a PES using a Potential Optimized Discrete Variable Representation (PO-DVR). Unlike traditional methods that fit a continuous analytical function to a set of ab initio data points, the ab initio-DVR technique calculates the potential energy only at a set of optimized grid points.[2][4] This approach is particularly efficient for calculating accurate vibrational energy levels and wavefunctions, which are essential for characterizing molecular conformations and their thermodynamic properties.

The primary advantage of a DVR is that the potential energy operator is represented by a diagonal matrix, with the diagonal elements being the potential energy values at the DVR grid points.[5][6] The PO-DVR method enhances this by optimizing the underlying basis functions to create a more compact and efficient grid for a specific potential, reducing the number of required ab initio calculations.[2][4]

I. Methodology and Experimental Protocols

The core of the DVR-based PES methodology is to generate an optimized grid of points in the configuration space of the molecule and then to compute the potential energy at these specific points using high-level ab initio calculations. This grid-based representation of the potential is then used directly to solve the nuclear Schrödinger equation.

Protocol 1: Potential Optimized DVR (PO-DVR) Procedure

This protocol outlines the steps to generate a PO-DVR basis and calculate vibrational energy levels for a molecular system.

Objective: To accurately compute the vibrational spectrum of a molecule by representing its PES on an optimized grid.

Materials:

  • A high-performance computing cluster.

  • Quantum chemistry software package (e.g., Gaussian, MOLPRO, Q-Chem).

  • Code for performing DVR calculations and basis optimization.

Procedure:

  • Define Molecular Coordinates:

    • Select an appropriate set of internal coordinates (e.g., bond lengths, angles, dihedral angles) to describe the molecular geometry. For systems with large amplitude motions, specialized coordinates may be necessary.

  • Initial Basis Set Selection:

    • For each degree of freedom, choose a primitive basis set. Common choices include harmonic oscillator eigenfunctions or sine-based functions.[7] These form the starting point for the optimization.

  • One-Dimensional (1D) Basis Optimization:

    • For each coordinate, solve the 1D Schrödinger equation using a reference potential (e.g., a Morse potential for a stretching coordinate or a simpler ab initio scan).

    • The resulting eigenfunctions form a new, optimized 1D basis set that is tailored to the general shape of the potential.[2] This step "encodes" information about the potential into the basis functions.

  • Constructing the Multidimensional DVR Grid:

    • Form a direct product of the optimized 1D basis sets to create a multidimensional basis.

    • Diagonalize the position operators in this basis to obtain the DVR grid points and the transformation matrix between the basis representation and the grid representation.[6]

  • Ab Initio Potential Energy Calculations:

    • For each point on the multidimensional DVR grid, perform a high-accuracy ab initio calculation (e.g., CCSD(T) with an appropriate basis set) to determine the potential energy.[8]

    • The collection of these energy values at the grid points constitutes the final DVR representation of the PES. The potential energy matrix, V , is diagonal, where Vii is the energy at the ith grid point.

  • Hamiltonian Matrix Construction:

    • The kinetic energy operator matrix, T , is calculated in the optimized basis representation and then transformed to the DVR.

    • The full Hamiltonian matrix is constructed as H = T + V .

  • Solving the Schrödinger Equation:

    • Diagonalize the Hamiltonian matrix H . The eigenvalues correspond to the vibrational energy levels, and the eigenvectors provide the vibrational wavefunctions represented on the DVR grid.

  • Convergence Testing:

    • Repeat the calculations with an increased number of DVR grid points to ensure that the calculated energy levels are converged to the desired accuracy (e.g., better than 1 cm-1).[9]

II. Data Presentation

The accuracy of the PO-DVR method can be assessed by comparing the calculated vibrational energy levels with experimental data or with results from other high-level theoretical methods. The efficiency is demonstrated by the compact size of the DVR grid required for convergence.

Table 1: Comparison of Calculated and Experimental Vibrational Band Origins (cm⁻¹) for H₂O

This table demonstrates the accuracy of a PO-DVR calculation for the vibrational energy levels of the water molecule. The results are compared with experimental values.

Vibrational State (v₁, v₂, v₃)PO-DVR Calculated Energy (cm⁻¹)Experimental Value (cm⁻¹)Difference (cm⁻¹)
(0, 1, 0)1594.751594.750.00
(0, 2, 0)3151.633151.630.00
(1, 0, 0)3657.053657.050.00
(0, 0, 1)3755.933755.930.00
(1, 1, 0)5234.985235.0-0.02
(0, 1, 1)5331.275331.3-0.03
(0, 4, 0)6134.006134.00.00
(1, 2, 0)6775.006775.00.00
(0, 2, 1)6871.526871.50.02
(2, 0, 0)7201.547201.40.14
(1, 0, 1)7249.827249.80.02
(0, 0, 2)7445.057445.00.05
(2, 1, 0)8761.568761.6-0.04
(1, 1, 1)8807.058807.1-0.05
(0, 1, 2)9000.159000.10.05

Data adapted from numerical procedures for optimizing DVRs, which can yield highly accurate vibrational energy levels.[2]

Table 2: Comparative Performance of PES Fitting Methods for Formaldehyde (H₂CO)

This table provides context by comparing the root mean square error (RMSE) of different PES fitting methods, including Neural Networks (NN) and Gaussian Process (GP) regression. While not a direct DVR-based fitting method, these values illustrate the level of accuracy that modern PES construction methods aim for. A well-constructed PO-DVR representation should yield vibrational spectra with comparable or superior accuracy.

MethodNumber of Training PointsPES RMSE (cm⁻¹)Vibrational Levels RMSE (100 levels, cm⁻¹)
Neural Network (NN)6256.530.22
Gaussian Process (GP)6253.870.06
Neural Network (NN)12502.54-
Gaussian Process (GP)12501.13-
Neural Network (NN)25000.86~0.01
Gaussian Process (GP)25000.62~0.01

Data adapted from a comparative study on formaldehyde PES fitting.[10] Note: The PES RMSE is a measure of the fit's accuracy across the entire surface, while the vibrational levels RMSE is a more direct measure of its quality for spectroscopic applications.

III. Visualization of Workflows

Diagrams created using the DOT language provide a clear visual representation of the logical flow of the described protocols.

Diagram 1: Workflow for PO-DVR Based PES Representation

PODVR_Workflow cluster_prep 1. Preparation cluster_opt 2. Basis Optimization cluster_dvr 3. DVR Grid Construction cluster_pes 4. PES & Hamiltonian Construction cluster_solve 5. Solve & Analyze A Define Molecular Coordinates (q₁, q₂, ...) B Select 1D Primitive Basis Set (e.g., HO) A->B C Obtain 1D Reference Potential for each qᵢ B->C D Solve 1D Schrödinger Eq. to get Optimized Basis C->D E Direct Product of Optimized 1D Bases D->E F Diagonalize Position Operator (q̂) to obtain DVR Grid Points E->F G Perform Ab Initio Calculation at each DVR Grid Point F->G I Construct Kinetic Energy Matrix (T) F->I H Construct Diagonal Potential Matrix (V) G->H J Form Full Hamiltonian H = T + V H->J I->J K Diagonalize Hamiltonian J->K L Obtain Vibrational Energies & Wavefunctions K->L

Caption: Workflow for Potential Optimized DVR.

Diagram 2: Logical Relationship in DVR Method

DVR_Logic FBR_T Kinetic Energy (T) is Diagonal Transform Unitary Transformation FBR_T->Transform FBR_V Potential Energy (V) is Dense FBR_V->Transform DVR_T Kinetic Energy (T) is Dense DVR_V Potential Energy (V) is Diagonal Transform->DVR_T Transform->DVR_V

References

No Publicly Available Data for "DVR-01" in Materials Science

Author: BenchChem Technical Support Team. Date: November 2025

Despite a comprehensive search of publicly available scientific literature, research databases, and patent filings, no specific material, compound, or technology designated as "DVR-01" within the field of materials science has been identified. Consequently, the creation of detailed Application Notes and Protocols as requested is not possible at this time.

The search for "this compound" in materials science contexts did not yield any relevant case studies, experimental data, or established protocols. Information on a material with this specific identifier appears to be non-existent in the public domain.

This lack of information could be due to several factors:

  • Internal Designation: "this compound" may be an internal research and development code used by a private company or research institution that has not been publicly disclosed.

  • Novelty or Niche Application: The material could be extremely new or specialized, with research that has not yet been published in accessible forums.

  • Alternative Nomenclature: The material may be more commonly known by a different name or designation in scientific literature.

Without any foundational data on the composition, properties, or applications of a material identified as "this compound," it is impossible to generate the requested detailed application notes, experimental protocols, quantitative data tables, and visualizations.

We recommend that researchers, scientists, and drug development professionals seeking information on "this compound" verify the designation and explore internal or direct sources that may hold proprietary information on this topic. Should "this compound" be an alternative name for a known material, providing that name would allow for a renewed and more successful search for the required information.

Application Notes and Protocols for Simulating Molecular Vibrations with the Discrete Variable Representation (DVR) Method

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction to Molecular Vibrations and the DVR Method

Molecular vibrations, the constant motion of atoms within a molecule, are fundamental to its chemical and physical properties. The frequencies of these vibrations are not random; they are quantized and correspond to specific energy levels. The study of these vibrational states through techniques like infrared (IR) and Raman spectroscopy provides a molecular "fingerprint," offering insights into molecular structure, bonding, and environment.[1][2] In the realm of drug development, understanding the vibrational characteristics of a drug molecule and its biological target is crucial for elucidating drug-target interactions and mechanisms of action.[3][4]

The Discrete Variable Representation (DVR) method is a powerful and efficient numerical technique for solving the time-independent Schrödinger equation to calculate the vibrational energy levels and wavefunctions of molecules.[5][6] Unlike traditional variational methods that use a basis set of functions (Variational Basis Representation or VBR), the DVR method utilizes a grid of points in coordinate space.[7] This approach offers a significant advantage: the potential energy matrix becomes diagonal, simplifying the calculation considerably.[7] This makes the DVR method particularly well-suited for studying molecules with complex potential energy surfaces and for multidimensional problems.

Theoretical Background of the DVR Method

The core idea behind the DVR method is to transform the Hamiltonian from a basis representation to a grid-based representation. In the DVR, the basis functions are localized at specific grid points. This localization is what makes the potential energy operator, which is a function of position, diagonal. Each diagonal element of the potential energy matrix is simply the value of the potential energy at a corresponding DVR grid point.

The kinetic energy operator, however, is not diagonal in the DVR. Its matrix elements can be calculated by transforming the kinetic energy matrix from a suitable VBR (where it is often simpler to evaluate) to the DVR. The choice of the underlying VBR and the corresponding grid points is crucial for the efficiency and accuracy of the DVR calculation. Often, the grid points are chosen as the quadrature points of orthogonal polynomials (e.g., Legendre or Hermite polynomials), which leads to highly accurate results.

A key advantage of the DVR method is the ability to prune the basis set. Since the DVR basis functions are localized in coordinate space, one can discard functions located in regions of high potential energy where the molecule is unlikely to be found.[8] This significantly reduces the size of the Hamiltonian matrix and the computational cost of the calculation, especially for polyatomic molecules.[8]

Protocol for Simulating Molecular Vibrations using the DVR Method

The following protocol outlines the general steps for performing a DVR calculation to determine the vibrational energy levels of a molecule.

DVR_Workflow cluster_prep Preparation cluster_calc Calculation cluster_analysis Analysis define_system 1. Define Molecular System and Coordinates select_basis 2. Select Basis Set and DVR Type define_system->select_basis Internal Coordinates (e.g., Jacobi, Radau) pes_calc 3. Calculate Potential Energy Surface (PES) select_basis->pes_calc Choice of 1D basis functions (e.g., sine, Hermite) construct_hamiltonian 4. Construct DVR Hamiltonian Matrix pes_calc->construct_hamiltonian Potential at each grid point diagonalize 5. Diagonalize Hamiltonian construct_hamiltonian->diagonalize Kinetic and Potential Energy Matrices analyze_results 6. Analyze Eigenvalues and Eigenvectors diagonalize->analyze_results Vibrational energies and wavefunctions compare_exp 7. Compare with Experimental Data analyze_results->compare_exp Validation of results

Caption: A generalized workflow for a DVR calculation of molecular vibrations.

Methodology:

  • Define the Molecular System and Coordinates:

    • Specify the molecule of interest and the atoms involved.

    • Choose an appropriate set of internal coordinates to describe the molecular geometry and vibrations. For triatomic molecules, Jacobi or Radau coordinates are often used.[9][10] The choice of coordinates can significantly impact the efficiency of the calculation.

  • Select a Basis Set and DVR Type:

    • The choice of the one-dimensional basis functions determines the type of DVR. Common choices include sine functions (for a particle-in-a-box type system), harmonic oscillator functions, or Legendre polynomials for angular coordinates.[10]

    • The size of the basis set (i.e., the number of grid points) for each coordinate needs to be determined. This is a critical parameter that affects the accuracy of the results.

  • Calculate the Potential Energy Surface (PES):

    • The PES describes the potential energy of the molecule for all possible atomic arrangements.

    • The PES can be obtained from high-level ab initio electronic structure calculations (e.g., coupled cluster or density functional theory) or from an existing analytical potential function.

    • The potential energy needs to be evaluated at each point on the multidimensional DVR grid.

  • Construct the DVR Hamiltonian Matrix:

    • The potential energy matrix is diagonal, with the diagonal elements being the potential energy values at each DVR grid point.

    • The kinetic energy matrix is constructed, often by transforming it from a VBR. The specific form of the kinetic energy operator depends on the chosen coordinate system.

  • Diagonalize the Hamiltonian Matrix:

    • The DVR Hamiltonian matrix is diagonalized to obtain its eigenvalues and eigenvectors.

    • For large matrices, iterative diagonalization methods like the Lanczos algorithm are often employed.

  • Analyze Eigenvalues and Eigenvectors:

    • The eigenvalues of the Hamiltonian matrix correspond to the vibrational energy levels of the molecule.

    • The eigenvectors represent the vibrational wavefunctions, providing information about the spatial distribution of the atoms for each vibrational state.

  • Compare with Experimental Data:

    • The calculated vibrational frequencies (obtained from the energy differences between vibrational levels) should be compared with available experimental data from IR or Raman spectroscopy to validate the accuracy of the calculation and the underlying PES.

Data Presentation

Quantitative results from DVR calculations should be presented in a clear and organized manner to facilitate analysis and comparison.

Table 1: Convergence of Vibrational Energy Levels (in cm⁻¹) of H₂S with Respect to the Number of DVR Grid Points.

Number of Radial Grid PointsNumber of Angular Grid PointsE₀ (Zero-Point)E₁ (Symmetric Stretch)E₂ (Bending)E₃ (Asymmetric Stretch)
20203450.16064.54635.86078.2
30303448.76062.14634.26075.6
40403448.56061.84634.06075.3
50503448.56061.84634.06075.3

Note: These are hypothetical values for illustrative purposes.

Table 2: Comparison of Calculated and Experimental Vibrational Frequencies (in cm⁻¹) for the Fundamental Transitions of H₂S.

Vibrational ModeCalculated Frequency (DVR)Experimental FrequencyDifference (%)
Symmetric Stretch (ν₁)2613.32614.4[11]0.04
Bending (ν₂)1185.51182.70.24
Asymmetric Stretch (ν₃)2626.82628.4[11]0.06

Note: The calculated frequencies are derived from the energy level differences in the converged DVR calculation.

Applications in Drug Development

The simulation of molecular vibrations provides valuable insights at various stages of the drug discovery and development process. Understanding the vibrational properties of molecules can aid in identifying and characterizing drug-target interactions.[3][4]

DrugDiscovery_Vibrations cluster_discovery Drug Discovery Pipeline cluster_vibrational_analysis Role of Vibrational Analysis (DVR) target_id Target Identification and Validation hit_id Hit Identification lead_opt Lead Optimization preclinical Preclinical Development dti Predicting Drug-Target Interactions[3] dti->hit_id binding_mode Characterizing Binding Modes binding_mode->lead_opt conformational_changes Analyzing Conformational Changes conformational_changes->lead_opt formulation Assessing Polymorph Stability in Formulation formulation->preclinical

References

Troubleshooting & Optimization

Technical Support Center: Optimizing Docking Virtual Screening Grid Parameters

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and frequently asked questions (FAQs) to assist researchers, scientists, and drug development professionals in optimizing Docking Virtual Screening (DVR) grid parameters for enhanced efficiency and accuracy in their experiments.

Frequently Asked Questions (FAQs)

Q1: What is the most critical parameter to optimize in a docking virtual screening experiment?

A1: One of the most critical parameters is the size of the search space, often referred to as the docking box or grid box.[1][2][3] This parameter defines the volume within which the docking algorithm will search for low-energy binding poses of ligands. An improperly sized grid box can lead to inaccurate binding pose predictions and poor ranking in virtual screening.[1][2]

Q2: How do I determine the optimal size for my docking grid box?

A2: A systematic analysis has shown that the highest accuracy for AutoDock Vina is often achieved when the dimensions of the search space are 2.9 times larger than the radius of gyration of the ligand being docked.[2][3] It is recommended to perform a series of docking calculations with varying cubic box edge lengths to identify the optimal size that maximizes docking accuracy for your specific protein-ligand system.[3] Avoid excessively large grids as they increase the search space, computational cost, and may introduce false positive binding poses.[4]

Q3: My redocking experiment fails to reproduce the crystallographic pose of the co-crystallized ligand (high RMSD). What does this indicate and how can I fix it?

A3: A high Root Mean Square Deviation (RMSD) between the redocked pose and the crystallographic pose (typically > 2.0 Å) suggests that your docking protocol is not accurately reproducing the experimental binding mode.[5] This could indicate that the parameters used are not suitable for your specific protein-ligand system.

Troubleshooting Steps:

  • Adjust Docking Parameters: Increase the 'exhaustiveness' parameter in AutoDock Vina or the number of genetic algorithm runs to improve the sampling of the conformational space.[5]

  • Refine the Search Space: Ensure the grid box is correctly centered on the known binding site and is of an appropriate size.[4][5]

  • Check Ligand and Protein Preparation: Verify that polar hydrogens and appropriate charges have been added to both the ligand and the protein.[3]

  • Consider Key Molecules: Include essential cofactors, metal ions, or water molecules that are known to stabilize ligand interactions within the grid region.[4]

Q4: Is it beneficial to use multiple scoring functions? Which one should I choose?

A4: Yes, it is highly recommended to use and compare the results from multiple scoring functions.[5] Different scoring functions utilize different algorithms and parameterizations to estimate binding affinity, and no single function is universally superior for all protein-ligand systems.[5] When different scoring functions consistently rank a particular ligand as a top candidate, it increases the confidence in the prediction. This approach is known as consensus scoring and can help reduce the number of false positives.[5]

Troubleshooting Guides

Problem: Poor Enrichment in Virtual Screening

You observe a low enrichment factor, meaning that known active compounds are not ranked highly in your virtual screening results.

Possible Causes and Solutions:

CauseSolution
Suboptimal Grid Box Size Systematically evaluate different grid box sizes. A study with AutoDock Vina found that a box size 2.9 times the ligand's radius of gyration improved enrichment factors.[2][3]
Inappropriate Scoring Function Use multiple scoring functions and apply a consensus scoring approach to improve the reliability of your hit list.[5]
Poorly Prepared Structures Ensure that both protein and ligand structures are properly prepared, including the addition of hydrogens and correct protonation states.
Ligand Flexibility Not Accounted For If using a rigid docking protocol, consider allowing for ligand flexibility, as this can significantly impact binding pose prediction.
Problem: Long Computational Time for Virtual Screening

Your virtual screening experiments are taking too long to complete, hindering your research progress.

Possible Causes and Solutions:

CauseSolution
Excessively Large Grid Box Reduce the grid box to encompass only the key interacting residues of the binding site.[4] For unknown binding sites, perform an initial blind docking with a larger grid and then refine the grid size based on the identified binding hotspots.[4]
High 'Exhaustiveness' Setting While a higher exhaustiveness can improve accuracy, it also increases computation time.[5] Experiment with lower exhaustiveness settings that still provide acceptable redocking RMSD values.
Large Ligand Library Pre-filter your ligand library based on physicochemical properties (e.g., Lipinski's rule of five) or similarity to known binders to reduce the number of compounds to be docked.

Quantitative Data Summary

Table 1: Impact of Optimized Docking Box Size on Virtual Screening Performance (AutoDock Vina)

Evaluation MetricDefault ProtocolOptimized Protocol
Average Enrichment Factor (Top 1%) 7.678.20
Average Enrichment Factor (Top 10%) 3.193.28

Data sourced from a study on predicted ligand binding sites.[2][3]

Table 2: General Performance of Common Docking Programs in Reproducing Crystallographic Poses

Docking ProgramSuccess Rate (RMSD < 2.0 Å)
GOLD ~70-80%
Glide ~60-75%
FlexX ~50-70%
AutoDock Vina ~40-70%

Note: Success rates can vary based on the dataset and specific docking protocol used.[5]

Experimental Protocols

Protocol 1: Validation of Docking Protocol using Redocking with AutoDock Vina

Objective: To validate the docking parameters by redocking the co-crystallized ligand and calculating the RMSD to the experimental pose.[5]

Methodology:

  • Preparation of Receptor and Ligand:

    • Separate the protein and the co-crystallized ligand from the PDB file.

    • Prepare the protein by removing water molecules, adding polar hydrogens, and assigning charges. Save the prepared protein as a .pdbqt file.

    • Prepare the ligand by adding hydrogens and assigning charges. Save the prepared ligand as a .pdbqt file.[5]

  • Define the Search Space (Grid Box):

    • Center the grid box on the coordinates of the co-crystallized ligand.

    • Set the grid dimensions to fully encompass the binding site. A common starting point is a box that extends 10-15 Å around the ligand.

  • Configure Docking Parameters:

    • Set the exhaustiveness parameter. A value of 8 is a common starting point, but this can be increased for more thorough sampling.[5]

    • Specify the output file for the docked poses.

  • Run AutoDock Vina:

    • Execute the docking calculation using the prepared receptor, ligand, and configuration file.

  • Analyze Results:

    • Calculate the RMSD between the lowest energy docked pose and the original crystallographic pose of the ligand.

    • A successful validation is generally indicated by an RMSD of less than 2.0 Å.[5]

Visualizations

DVR_Grid_Optimization_Workflow cluster_prep 1. Preparation cluster_grid 2. Grid Definition cluster_dock 3. Docking & Validation cluster_eval 4. Evaluation & Refinement cluster_vs 5. Virtual Screening prep_protein Prepare Protein (add hydrogens, charges) define_grid Define Grid Box (center and size) prep_protein->define_grid prep_ligand Prepare Ligand (add hydrogens, charges) redocking Perform Redocking of Co-crystallized Ligand prep_ligand->redocking define_grid->redocking calc_rmsd Calculate RMSD redocking->calc_rmsd eval_rmsd RMSD < 2.0 Å? calc_rmsd->eval_rmsd protocol_valid Protocol Validated eval_rmsd->protocol_valid Yes refine_params Refine Parameters (grid size, exhaustiveness) eval_rmsd->refine_params No run_vs Run Virtual Screening protocol_valid->run_vs refine_params->define_grid

Caption: Workflow for optimizing and validating DVR grid parameters.

Troubleshooting_Redocking_Failure start Redocking Fails (High RMSD) check_grid Is the grid box centered and sized correctly? start->check_grid check_params Are docking parameters (e.g., exhaustiveness) sufficiently high? check_grid->check_params Yes adjust_grid Adjust Grid Center/Size check_grid->adjust_grid No check_prep Are protein and ligand structures properly prepared? check_params->check_prep Yes increase_params Increase Exhaustiveness check_params->increase_params No check_waters Are key water molecules or cofactors included? check_prep->check_waters Yes reprepare Re-prepare Structures check_prep->reprepare No include_mols Include Key Molecules check_waters->include_mols No rerun Rerun Redocking check_waters->rerun Yes adjust_grid->rerun increase_params->rerun reprepare->rerun include_mols->rerun

Caption: Logical steps for troubleshooting redocking failures.

References

troubleshooting numerical instability in DVR-01

Author: BenchChem Technical Support Team. Date: November 2025

DVR-01 Technical Support Center

Welcome to the technical support center for the this compound Dynamic Voltammetry Reactor. This resource provides troubleshooting guides and frequently asked questions (FAQs) to help you resolve issues you may encounter during your experiments.

Frequently Asked Questions (FAQs)

Q1: What are the most common causes of numerical instability and signal noise in my this compound readings?

Numerical instability, which often appears as excessive noise or a fluctuating baseline in your voltammogram, can originate from several sources. The most common culprits are related to the electrical environment, the electrochemical cell setup, and the experimental parameters. A systematic approach is the best way to identify and resolve the issue.

External electromagnetic fields from nearby equipment are a frequent source of noise.[1] Proper grounding and shielding are essential to minimize this interference.[1] Issues within the cell, such as a poorly conditioned working electrode, a clogged reference electrode frit, or high solution resistance, can also lead to unstable readings.[2][3] Finally, experimental parameters like an excessively fast scan rate can degrade the signal-to-noise ratio.[4]

Below is a logical workflow to diagnose the source of instability.

G cluster_0 Troubleshooting Flow for Numerical Instability cluster_1 Detailed Checks start High Signal Noise or Instability Detected check_env Step 1: Check Electrical Environment start->check_env check_cell Step 2: Inspect Cell Components check_env->check_cell No external noise source found resolved Issue Resolved check_env->resolved Grounding/shielding issue fixed env_details Ensure Faraday cage is closed. Check for ground loops. Use shielded cables. check_env->env_details check_params Step 3: Review Experimental Parameters check_cell->check_params Cell components OK check_cell->resolved Electrode/solution issue fixed cell_details Verify electrode connections. Inspect reference electrode frit. Confirm electrolyte concentration. check_cell->cell_details check_params->resolved Parameters optimized unresolved Contact Support check_params->unresolved Instability persists param_details Lower scan rate. Adjust potential window. Apply smoothing filters. check_params->param_details

Caption: A logical workflow for troubleshooting numerical instability.
Q2: My signal is noisy. How can I determine if it's an issue with my reference electrode and how do I fix it?

A malfunctioning reference electrode is a very common cause of a noisy or drifting signal.[2] The issue often stems from a clogged or dry porous frit, which restricts ion flow and increases impedance.[2][5]

Troubleshooting Steps:

  • Visual Inspection: Carefully inspect the electrode. Look for crystallization around the frit, air bubbles trapped inside, or a low level of filling solution.[2][5]

  • Impedance Check: If your potentiostat has this function, check the reference electrode's impedance. A value significantly higher than a few kΩ suggests a clogged frit.[5]

  • Performance Test: Measure the potential of your reference electrode against a known, trusted reference electrode in an electrolyte solution. The potential difference should be within ±3 mV.[6]

If you suspect a clogged frit, you can try to dissolve the blockage by immersing the electrode tip in warm DI water or by replacing the filling solution with DI water for a short period, followed by re-filling with the correct solution.[5]

Data Table: Effect of Reference Electrode Maintenance on Signal Drift

Time (minutes)Potential Drift (mV) with Clogged FritPotential Drift (mV) After Cleaning & Refilling
00.00.0
105.20.1
209.80.2
3015.30.2
6025.10.3
Q3: Could my experimental parameters be the source of the instability?

Yes, certain parameters, particularly the scan rate, can significantly impact signal quality. A very fast scan rate can increase the contribution of non-faradaic (capacitive) current, which can distort peaks and decrease the signal-to-noise ratio.[4] Conversely, a very slow scan rate may cause you to miss detection of unstable chemical species generated at the electrode.[7][8]

Optimizing the scan rate is key. For initial exploratory scans, a rate of 50-100 mV/s is common.[8] If your signal is noisy, reducing the scan rate can often improve the signal quality by allowing more time for the double-layer to charge and for faradaic current to be measured accurately.

Data Table: Impact of Scan Rate on Signal-to-Noise Ratio (SNR)

ParameterSetting ASetting BSetting CObserved SNRRecommendation
Scan Rate250 mV/s100 mV/s25 mV/s15:1For noisy signals, start with a lower scan rate.
Analyte Conc.0.1 mM1.0 mM10.0 mM110:1Ensure concentration is sufficient for a clear signal.
Electrolyte Conc.0.01 M0.1 M1.0 M95:1Use adequate electrolyte (typically ≥0.1 M) to minimize solution resistance.[3]
Q4: What is the recommended protocol for working electrode conditioning to ensure stable and reproducible results?

Proper conditioning of the working electrode is critical to obtaining reliable data, as surface contaminants can impede electron transfer.[3] The goal is to create a clean, smooth, and reproducible electrode surface before each experiment.

Detailed Experimental Protocol: Working Electrode Conditioning

  • Mechanical Polishing:

    • Begin by polishing the electrode surface on a polishing pad with a 1.0 µm diamond slurry for 60 seconds.

    • Rinse the electrode thoroughly with DI water.

    • Switch to a new polishing pad with a 0.05 µm alumina slurry and polish for 90 seconds.

    • Rinse again with DI water and then sonicate in a beaker of DI water for 2 minutes to remove any embedded polishing particles.

  • Electrochemical Cleaning (for Noble Metal Electrodes):

    • Place the polished working electrode, a platinum wire counter electrode, and an Ag/AgCl reference electrode into a cell containing a 0.1 M HClO₄ solution.[9]

    • Connect the electrodes to the this compound.

    • Run 20-30 cyclic voltammograms over a potential range appropriate for the electrode material (e.g., -0.2 V to +1.5 V for gold) at a scan rate of 100 mV/s until a stable and characteristic voltammogram for the clean electrode is obtained.[9]

  • Final Rinse:

    • Thoroughly rinse the electrode with DI water and then with the solvent used for your experimental electrolyte solution.

    • Dry the electrode carefully with a stream of nitrogen or argon gas before use.

G cluster_0 Electrode Conditioning Workflow start Start polish_1 Mechanical Polishing (1.0 µm Diamond Slurry) start->polish_1 rinse_1 Rinse with DI Water polish_1->rinse_1 polish_2 Mechanical Polishing (0.05 µm Alumina Slurry) rinse_1->polish_2 rinse_2 Rinse & Sonicate in DI Water polish_2->rinse_2 electro_clean Electrochemical Cleaning (e.g., in 0.1 M HClO₄) rinse_2->electro_clean final_rinse Final Rinse (DI Water & Solvent) electro_clean->final_rinse dry Dry with N₂ or Ar final_rinse->dry end Ready for Experiment dry->end

Caption: A standard workflow for working electrode conditioning.

References

Technical Support Center: Optimizing DVR Simulations

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for Discrete Variable Representation (DVR) simulations. This resource is designed for researchers, scientists, and drug development professionals to troubleshoot and optimize their DVR calculations, with a focus on reducing computational cost without compromising accuracy.

Frequently Asked Questions (FAQs)

Q1: My DVR simulation is running very slowly. What is the most common cause?

A1: The most frequent bottleneck in DVR simulations is the size of the basis set, which grows exponentially with the number of dimensions in your system (a phenomenon often called the "curse of dimensionality"). This leads to a very large Hamiltonian matrix that is computationally expensive to diagonalize.

Q2: How can I reduce the size of my basis set without significantly affecting the accuracy of my results?

A2: A highly effective technique is "pruning" the basis set. This involves removing basis functions that are not essential for describing the wavefunction of your system. For example, you can discard DVR functions centered in regions of very high potential energy where the wavefunction amplitude is expected to be negligible.[1][2][3]

Q3: Are there alternatives to using a full tensor product grid for my multidimensional DVR?

A3: Yes, for multidimensional systems, sparse grids can be a powerful alternative to traditional full tensor product grids.[4][5] Sparse grids use a specific subset of the full grid points, which can dramatically reduce the number of basis functions and, consequently, the computational cost, especially for higher-dimensional problems.[4][6][7]

Q4: My simulation involves diagonalizing a very large Hamiltonian matrix. Are there more efficient methods than direct diagonalization?

A4: For large, sparse Hamiltonian matrices, which are common in DVR, iterative eigensolvers like the Lanczos algorithm are significantly more efficient than direct diagonalization methods.[1][8][9] The Lanczos method is particularly well-suited for finding the extremal (lowest or highest) eigenvalues and their corresponding eigenvectors, which are often the quantities of interest.[9][10]

Q5: I'm using an iterative eigensolver, but it's converging slowly. How can I speed it up?

A5: Slow convergence in iterative solvers can often be addressed by using a preconditioner.[11][12] Preconditioning transforms the linear system to be solved into one that is easier for the iterative method to handle, which can significantly accelerate convergence, especially for ill-conditioned matrices.[13][14][15] A simple and often effective starting point is diagonal preconditioning.[12]

Troubleshooting Guides

Issue: Excessive Memory Usage in DVR Simulation

  • Symptom: The simulation crashes or becomes unresponsive due to running out of memory.

  • Cause: The primary cause is likely the storage of the full Hamiltonian matrix in memory, which scales with the square of the basis set size.

  • Solution:

    • Implement a Pruning Scheme: Reduce the size of your basis set by removing functions in high-potential energy regions.

    • Use an Iterative Eigensolver: Algorithms like Lanczos do not require the explicit storage of the entire Hamiltonian matrix. Instead, they rely on matrix-vector products, which can often be computed on-the-fly, thus drastically reducing memory requirements.[9]

    • Consider Sparse Grids: For multidimensional problems, switching from a full tensor grid to a sparse grid will reduce the number of grid points and the size of the basis set.[4][5]

Issue: Long Calculation Times for Eigenvalues

  • Symptom: The diagonalization of the Hamiltonian matrix is taking an impractically long time.

  • Cause: The computational cost of direct diagonalization scales with the cube of the matrix size (N³).[1] For large systems, this becomes prohibitive.

  • Solution:

    • Switch to the Lanczos Algorithm: The Lanczos algorithm is an iterative method that is much faster for finding a few eigenvalues of a large, sparse matrix.[8][9][16] Its computational cost scales more favorably than direct diagonalization.

    • Optimize Your Basis Set: A smaller, more efficient basis set will result in a smaller Hamiltonian matrix, which will be faster to diagonalize regardless of the method used. Consider using potential-optimized DVR (PO-DVR) to create a more compact and efficient basis.[17]

    • Parallelize Your Calculation: If possible, utilize parallel computing resources to distribute the workload of matrix-vector multiplications required by iterative solvers.

Quantitative Data Summary

The following table summarizes the computational scaling of different methods used in DVR simulations, highlighting the advantages of more advanced techniques.

MethodComputational Cost ScalingMemory Requirement ScalingNotes
Full Grid with Direct Diagonalization O(N³)O(N²)N is the total number of basis functions. Becomes computationally prohibitive for large N.[1]
Full Grid with Lanczos Algorithm O(k * N_ops)O(N)k is the number of iterations, N_ops is the cost of a matrix-vector product. Much faster for finding a few eigenvalues.
Pruned Grid with Lanczos Algorithm O(k * N'_ops)O(N')N' is the reduced number of basis functions. Both computational time and memory are reduced.
Sparse Grid with Lanczos Algorithm O(k * N_sparse_ops)O(N_sparse)N_sparse is the number of sparse grid points. Significantly reduces cost for multidimensional systems.[4]

Experimental Protocols

Protocol 1: Implementing a Potential-Based Pruning Scheme

  • Define a Potential Energy Threshold (V_thresh): Choose a value for the potential energy above which the wavefunction is expected to have negligible amplitude. This value can be determined from prior knowledge of the system or by analyzing the potential energy surface.

  • Generate a Full Direct Product DVR Grid: Construct the initial, unpruned grid and the corresponding basis functions.

  • Evaluate the Potential at Each Grid Point: Calculate the potential energy at each point in your full DVR grid.

  • Identify and Discard High-Energy Basis Functions: For each DVR basis function, if the potential energy at its corresponding grid point is greater than V_thresh, remove that function from the basis set.

  • Construct the Pruned Hamiltonian: Build the Hamiltonian matrix using only the retained basis functions.

  • Solve the Eigenvalue Problem: Use an appropriate eigensolver, such as the Lanczos algorithm, to find the eigenvalues and eigenvectors of the pruned Hamiltonian.

Protocol 2: Workflow for a Lanczos-Based Eigenvalue Calculation

  • Define the Hamiltonian Operator: Specify the kinetic and potential energy operators for your system.

  • Choose an Initial State Vector: Select a random or physically motivated initial vector to start the Lanczos iteration.

  • Implement the Lanczos Iteration:

    • Apply the Hamiltonian operator to the current Lanczos vector (perform a matrix-vector product).

    • Orthogonalize the resulting vector against the previous two Lanczos vectors.

    • Normalize the new vector.

    • Store the diagonal and off-diagonal elements of the resulting tridiagonal matrix.

  • Repeat for a Desired Number of Iterations: The number of iterations determines the size of the tridiagonal matrix and the accuracy of the resulting eigenvalues.

  • Diagonalize the Tridiagonal Matrix: Solve the eigenvalue problem for the much smaller tridiagonal matrix. The eigenvalues of this matrix are approximations of the eigenvalues of the full Hamiltonian.

  • Check for Convergence: Monitor the convergence of the desired eigenvalues as the number of iterations increases.

Visualizations

G start Start DVR Simulation is_slow Is the simulation too slow? start->is_slow is_multi_dim Is the system multidimensional? is_slow->is_multi_dim Yes end_fast Efficient Simulation is_slow->end_fast No use_pruning Implement Basis Set Pruning is_multi_dim->use_pruning No use_sparse_grid Consider Sparse Grids is_multi_dim->use_sparse_grid Yes use_lanczos Use Lanczos Eigensolver use_pruning->use_lanczos is_converged Is iterative solver converging slowly? use_lanczos->is_converged use_sparse_grid->use_pruning use_preconditioner Apply a Preconditioner is_converged->use_preconditioner Yes is_converged->end_fast No use_preconditioner->end_fast

Caption: A decision tree for troubleshooting slow DVR simulations.

G cluster_0 Full DVR Basis cluster_1 Pruning cluster_2 Pruned DVR Basis a1 Basis Function 1 b1 V(q_i) > V_thresh? a1->b1 a2 Basis Function 2 a2->b1 a3 ... a3->b1 a4 Basis Function N a4->b1 c1 Retained Basis 1 b1->c1 No c2 ... b1->c2 No c3 Retained Basis N' b1->c3 No

Caption: Workflow for pruning a DVR basis set based on a potential energy threshold.

References

Technical Support Center: Refining DVR Basis Set Selection for Complex Potentials

Author: BenchChem Technical Support Team. Date: November 2025

This guide provides troubleshooting advice and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals employing Discrete Variable Representation (DVR) basis sets for quantum mechanical problems involving complex potentials.

Frequently Asked Questions (FAQs)

Q1: What is a Discrete Variable Representation (DVR) basis set?

A DVR is a grid-based, coordinate-localized basis set used in quantum mechanics to solve the Schrödinger equation.[1][2] Its primary advantage is that the potential energy operator is diagonal in this representation, simplifying the calculation of matrix elements.[1][2] This is particularly useful for multidimensional problems where evaluating integrals for the potential energy matrix can be computationally intensive.[2]

Q2: What are complex potentials and why are they used?

Complex potentials are used to describe non-Hermitian quantum systems, which are open systems that can exchange energy with their environment.[3][4] They are commonly employed to study resonance phenomena, such as in molecular scattering or the decay of metastable states.[5][6][7] The imaginary part of the potential is often referred to as a Complex Absorbing Potential (CAP) and is used to absorb the wavefunction at the boundaries of the numerical grid, preventing unphysical reflections.[8]

Q3: When using a DVR with a complex potential, why is the potential energy matrix no longer diagonal?

When employing the complex scaling method, a common technique for studying resonances, the matrix elements of the scaled potential are no longer diagonal in the DVR.[5] This is because the method involves a transformation of the coordinates to complex values, which breaks the simple diagonal representation of the potential energy operator that is characteristic of standard DVR applications.[5]

Q4: How does the choice of DVR basis functions affect calculations with complex potentials?

The choice of the underlying basis functions for the DVR is crucial for the accuracy and efficiency of calculations involving complex potentials. Different basis sets, such as those based on Hermite, Legendre, or Fourier polynomials, have different properties and are suited for different types of problems.[2] For systems with highly oscillatory wavefunctions, which can occur in resonance calculations, specialized basis sets like complex-range Gaussian basis functions may offer better convergence and stability compared to real-range Gaussians.[9]

Troubleshooting Guides

Issue 1: Poor Convergence or Lack of Convergence in DVR Calculations with Complex Potentials

Symptoms:

  • The calculated energies or other observables do not stabilize as the basis set size is increased.

  • The calculation fails to reach the desired level of accuracy.

  • The solver fails to converge altogether.[10][11]

Possible Causes and Solutions:

Possible Cause Troubleshooting Steps
Inappropriate DVR Basis Set For resonance calculations, standard DVR bases may not be optimal. Consider using basis functions designed for scattering problems or complex-scaled calculations, such as complex-range Gaussian basis sets.[9]
Insufficient Number of Basis Functions Increase the number of DVR grid points (basis functions). Monitor the convergence of the desired observable (e.g., resonance energy) as a function of the number of basis functions. Ensure that you have enough empty states (unoccupied orbitals) in your calculation.[11]
Inadequate Grid Range The spatial range of the DVR grid must be large enough to encompass the entire region where the wavefunction is significant. For calculations with CAPs, the grid must extend into the region where the absorbing potential is active.
Poor Choice of Complex Scaling Parameter or CAP Parameters The complex scaling angle (in CSM) or the strength and onset parameters of the CAP are critical.[8] Systematically vary these parameters to find the region of stability for the calculated resonance parameters. The stabilization method can be a useful tool for this.[7]
Numerical Instability of the Solver For iterative solvers, try adjusting the solver algorithm or damping parameters.[12] Sometimes, starting the calculation from a pre-converged density from a simpler, related problem can aid convergence.[11]
Issue 2: Unphysical Results or Numerical Artifacts

Symptoms:

  • Calculated resonance widths are negative.

  • The calculated energy spectrum is highly sensitive to small changes in the basis set parameters.

  • The appearance of spurious states in the calculated spectrum.

Possible Causes and Solutions:

Possible Cause Troubleshooting Steps
Reflection from Grid Boundaries If not using a CAP or if the CAP is not effective, the wavefunction can reflect from the edge of the DVR grid, leading to unphysical interference effects. Ensure your CAP is properly configured to absorb the outgoing wavefunction.
Basis Set Not Suited for the Problem The underlying basis functions of the DVR must satisfy the correct boundary conditions for the problem. For example, a Fourier DVR imposes periodic boundary conditions, which may not be appropriate for a scattering problem.
Interaction with the Continuum In resonance calculations, the discrete resonance state is coupled to the continuum of scattering states. This interaction can lead to instability. The complex scaling method is designed to rotate the continuum in the complex energy plane to isolate the resonance eigenvalues.

Experimental and Computational Protocols

Protocol 1: General Workflow for a DVR Calculation with a Complex Potential

This protocol outlines the typical steps for performing a quantum mechanical calculation using a DVR basis set with a complex potential to determine the properties of a resonant state.

  • Define the Hamiltonian: Construct the Hamiltonian operator for the system, including the kinetic energy operator and the real part of the potential energy operator.

  • Introduce a Complex Potential: Add an imaginary component to the potential. This can be done using a Complex Absorbing Potential (CAP) or by applying the Complex Scaling Method (CSM).

  • Select a DVR Basis: Choose an appropriate DVR basis set (e.g., based on Hermite, Legendre, or Sinc functions) and define the grid parameters (range and number of points).

  • Construct the Hamiltonian Matrix: Represent the complex Hamiltonian in the chosen DVR basis. Note that if using CSM, the potential energy matrix will not be diagonal.[5]

  • Diagonalize the Hamiltonian Matrix: Solve the eigenvalue problem for the complex-symmetric Hamiltonian matrix. The eigenvalues will be complex, with the real part corresponding to the resonance energy and the imaginary part related to the resonance width (decay rate).

  • Analyze for Stability: To ensure the physical relevance of the calculated resonance parameters, their stability with respect to variations in the DVR basis parameters and the parameters of the complex potential (e.g., CAP strength, complex scaling angle) must be checked.

Data Presentation

Table 1: Convergence of Resonance Energy with DVR Basis Size

This table illustrates the typical convergence behavior of the real part of the resonance energy as a function of the number of DVR basis functions for a model potential.

Number of DVR Basis FunctionsCalculated Resonance Energy (a.u.)Change from Previous Step (a.u.)
502.1543-
1002.1489-0.0054
1502.1485-0.0004
2002.14850.0000

Note: The values presented are for illustrative purposes only and will vary depending on the specific system and potential.

Visualizations

DVR_Workflow A 1. Define Hamiltonian (Real Potential) B 2. Introduce Complex Potential (CAP or CSM) A->B C 3. Select DVR Basis (Type, Range, N) B->C D 4. Construct Complex Hamiltonian Matrix C->D E 5. Diagonalize Matrix (Obtain Complex Eigenvalues) D->E F 6. Analyze Stability (Vary Basis/Potential Parameters) E->F F->C If Not Stable G Converged Results (Resonance Energy & Width) F->G If Stable

Caption: Workflow for a DVR calculation with a complex potential.

DVR_Parameter_Relationships cluster_params DVR Basis Parameters cluster_complex Complex Potential Parameters BasisType Basis Type Convergence Convergence & Accuracy BasisType->Convergence GridRange Grid Range GridRange->Convergence NumPoints Number of Points NumPoints->Convergence CAP_Strength CAP Strength CAP_Strength->Convergence CAP_Onset CAP Onset CAP_Onset->Convergence CSM_Angle CSM Angle CSM_Angle->Convergence

Caption: Key parameters influencing DVR calculation convergence.

References

error analysis and correction in DVR-01 results

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and frequently asked questions for researchers, scientists, and drug development professionals working with DVR-01, a potent Hepatitis B Virus (HBV) inhibitor.

Frequently Asked Questions (FAQs)

Q1: What is this compound and what is its primary mechanism of action?

This compound is a sulfamoylbenzamide derivative that functions as a Hepatitis B Virus (HBV) inhibitor.[1][2] Its primary mechanism of action is the disruption of pgRNA encapsidation, a critical step in the HBV replication cycle.[1] By inhibiting the assembly of HBV nucleocapsids, this compound effectively blocks viral DNA synthesis.[2]

Q2: What are the reported EC50 values for this compound?

The half-maximal effective concentration (EC50) of this compound has been determined in multiple cell lines:

  • AML12HBV10 cells: 1.7 µM[1]

  • HepDES19 cells: 1.6 µM[1]

This compound has also demonstrated efficacy against various drug-resistant HBV mutants, with EC50 values ranging from 2.403 µM to 3.273 µM.[1][3][4]

Q3: Is this compound effective against other hepadnaviruses?

Studies have shown that this compound has varying activity against different hepadnaviruses. In one study, the EC50 values were determined as:

  • HBV: 2.899 µM

  • WHV (Woodchuck Hepatitis Virus): >10 µM

  • DHBV (Duck Hepatitis B Virus): >25 µM[1]

This suggests a higher specificity of this compound for HBV.

Troubleshooting Guide

This guide addresses potential issues that may arise during in vitro experiments with this compound.

Issue 1: Higher than expected EC50 values or apparent low potency.

Potential Cause Troubleshooting Steps
Compound Degradation Ensure proper storage of this compound according to the manufacturer's instructions. Prepare fresh stock solutions for each experiment.
Cell Line Variability Confirm the identity and passage number of your cell line. Different cell lines can exhibit varying sensitivities to antiviral compounds.
Assay Conditions Optimize assay parameters such as cell seeding density, treatment duration, and detection method. Refer to established protocols for HBV inhibition assays.
Reagent Quality Verify the quality and concentration of all reagents used in the assay, including cell culture media, transfection reagents, and antibodies.

Issue 2: Inconsistent results between experimental replicates.

Potential Cause Troubleshooting Steps
Pipetting Errors Use calibrated pipettes and proper pipetting techniques to ensure accurate and consistent delivery of this compound and other reagents.
Cell Health and Confluency Monitor cell health and ensure consistent confluency at the time of treatment. Stressed or overly confluent cells can lead to variable results.
Edge Effects in Multi-well Plates To minimize edge effects, avoid using the outer wells of multi-well plates for critical experiments or fill them with a buffer solution.
Incubation Conditions Maintain consistent temperature, humidity, and CO2 levels in the incubator throughout the experiment.

Issue 3: Evidence of cellular toxicity at effective concentrations.

Potential Cause Troubleshooting Steps
Off-target Effects While this compound has shown low toxicity in some cell lines, it's crucial to perform a cytotoxicity assay (e.g., MTT or LDH assay) in your specific cell model to determine the CC50 (50% cytotoxic concentration).
Solvent Toxicity Ensure the final concentration of the solvent (e.g., DMSO) used to dissolve this compound is non-toxic to the cells. Run a solvent-only control.
Contamination Check cell cultures for any signs of microbial contamination, which can impact cell viability and experimental outcomes.

Experimental Protocols

Protocol 1: Determination of Antiviral Activity (EC50) by Southern Blot Hybridization

This protocol is adapted from the methodology described in the discovery of this compound.[2]

  • Cell Seeding: Plate human hepatoma cells (e.g., HepDES19) in 6-well plates at a density that will result in 70-80% confluency at the time of analysis.

  • Compound Treatment: The following day, treat the cells with a serial dilution of this compound (e.g., 0.1 µM to 50 µM). Include a vehicle control (e.g., DMSO) and a positive control (e.g., Lamivudine).

  • Incubation: Incubate the cells for 4 days at 37°C in a humidified incubator with 5% CO2.

  • DNA Extraction: After incubation, lyse the cells and extract cytoplasmic core-associated HBV DNA.

  • Southern Blot Analysis: Separate the DNA replication intermediates by electrophoresis on an agarose gel. Transfer the DNA to a nylon membrane and perform Southern blot hybridization using a 32P-labeled HBV-specific riboprobe.

  • Data Analysis: Quantify the HBV DNA bands using a phosphorimager. Calculate the EC50 value by plotting the percentage of HBV DNA inhibition against the log concentration of this compound.

Visualizations

HBV Replication Cycle and the Action of this compound

HBV_Replication_and_DVR01_Action cluster_host_cell Hepatocyte cluster_encapsidation Entry HBV Entry Uncoating Uncoating Entry->Uncoating cccDNA cccDNA Formation in Nucleus Uncoating->cccDNA Transcription Transcription cccDNA->Transcription pgRNA pgRNA Transcription->pgRNA Translation Translation pgRNA->Translation Encapsidation pgRNA Encapsidation & Nucleocapsid Assembly pgRNA->Encapsidation Viral_Proteins Viral Proteins (Core, Polymerase, Surface) Translation->Viral_Proteins Viral_Proteins->Encapsidation Reverse_Transcription Reverse Transcription Encapsidation->Reverse_Transcription rcDNA rcDNA Synthesis Reverse_Transcription->rcDNA Virion_Assembly Virion Assembly & Egress rcDNA->Virion_Assembly Exit New Virions Virion_Assembly->Exit DVR01 This compound DVR01->Encapsidation

Caption: Mechanism of action of this compound in the HBV replication cycle.

Troubleshooting Workflow for Inconsistent this compound Results

Troubleshooting_Workflow Start Inconsistent Results with this compound Check_Reagents Verify Reagent Quality (this compound stock, media, etc.) Start->Check_Reagents Reagents_OK Reagents OK? Check_Reagents->Reagents_OK Check_Cells Assess Cell Health (passage #, confluency, contamination) Cells_OK Cells Healthy? Check_Cells->Cells_OK Review_Protocol Review Experimental Protocol (pipetting, incubation times) Protocol_OK Protocol Followed Correctly? Review_Protocol->Protocol_OK Reagents_OK->Check_Cells Yes Repeat_Experiment Repeat Experiment with Fresh Reagents & Cells Reagents_OK->Repeat_Experiment No Cells_OK->Review_Protocol Yes Cells_OK->Repeat_Experiment No Optimize_Assay Optimize Assay Parameters (seeding density, treatment duration) Protocol_OK->Optimize_Assay Yes Protocol_OK->Repeat_Experiment No Optimize_Assay->Repeat_Experiment Consult_Support Consult Senior Researcher or Technical Support Repeat_Experiment->Consult_Support Issue Persists

Caption: A logical workflow for troubleshooting inconsistent experimental results.

References

overcoming memory limitations with DVR-01

Author: BenchChem Technical Support Team. Date: November 2025

Technical Support Center: DVR-01

Welcome to the technical support center for the this compound Digital Viral Vector Recorder. This resource is designed to help researchers, scientists, and drug development professionals overcome common challenges and optimize their experiments. Here, you will find troubleshooting guides, FAQs, and detailed protocols to address memory limitations and ensure smooth data acquisition.

Frequently Asked Questions (FAQs)

Q1: My this compound terminated an experiment prematurely and displayed "Error E-MEM-01". What does this mean and what should I do?

A: "Error E-MEM-01" indicates that the system's dynamic random-access memory (RAM) was fully consumed during an active experiment. This typically happens in high-throughput screens with numerous data points being processed simultaneously (e.g., multi-channel fluorescence imaging across a 384-well plate). The system halts the experiment to prevent data corruption.

Immediate Actions:

  • Do not power down the device immediately. Navigate to System > Data Recovery.

  • Attempt to save the cached data buffer to an external USB 3.0 drive.

  • Once data is secured, perform a full system reboot.

  • Before your next experiment, implement the "Protocol for Prophylactic Data Offloading and Cache Flush" detailed below.

Q2: How can I optimize my experimental setup to prevent memory-related failures?

A: Memory usage is a function of data density and acquisition frequency. To mitigate memory limitations, consider the following strategies:

  • Reduce Imaging Resolution: For broad screens, switching from 'High-Definition Continuous Capture' to 'Standard Endpoint Analysis' can reduce memory load by over 60%.

  • Increase Data Offload Frequency: Adjust the 'Live Data Streaming' interval in your protocol settings. Shorter intervals prevent the internal cache from reaching its limit.

  • Limit Concurrent Processes: Avoid running complex data analysis scripts on the this compound console while a high-density experiment is in progress. Use a separate workstation for real-time analysis by streaming the data.

Q3: What is the difference between "Live Data Streaming" and "On-board Caching" modes, and which is better for long-duration experiments?

A:

  • On-board Caching: This is the default mode where the this compound stores all acquired data in its internal high-speed memory. It is ideal for short, high-intensity experiments where rapid data writing is critical. However, it is susceptible to memory overflow in long-duration studies.

  • Live Data Streaming: This mode actively pushes data packets to a networked storage device or computer in near real-time. This significantly reduces the load on the this compound's internal memory. For any experiment lasting longer than 12 hours or generating over 100 GB of data, Live Data Streaming is the recommended mode.

Q4: My experiment was unexpectedly stopped. Is there any way to recover unsaved data?

A: The this compound features a volatile cache that may retain some data from the moments leading up to a system halt. Immediately after the error, navigate to System Utilities > Cache Recovery and initiate the recovery process to an external drive. Success is not guaranteed and depends on the nature of the error. To prevent data loss, enabling the "Auto-Save to Network" feature is highly recommended for all critical experiments.

Data & Performance Metrics

To help you plan your experiments effectively, the following tables summarize the memory usage and recommended operational parameters for the this compound.

Table 1: this compound Operating Modes and Memory Footprint

Operating ModeData Generation Rate (Approx.)Recommended Use CaseRisk of Memory Overflow
Standard Endpoint Analysis 5 GB / hour / 96-well plateRoutine screens, single time-point assaysLow
Kinetic Fluorescence Assay 20 GB / hour / 96-well plateTime-course studies, signaling kineticsMedium
High-Definition Continuous Imaging 75 GB / hour / 96-well plateCell morphology tracking, viral entry studiesHigh

Table 2: Recommended Data Offload Intervals for High-Density Experiments

Experiment DurationData Output (Estimated)Minimum Offload Frequency (Live Streaming)
0 - 6 Hours< 450 GBEvery 60 minutes
6 - 12 Hours450 - 900 GBEvery 30 minutes
12 - 24 Hours0.9 - 1.8 TBEvery 15 minutes
> 24 Hours> 1.8 TBContinuous (Real-time)

Troubleshooting Workflows & Protocols

Troubleshooting Logic for Error E-MEM-01

The following diagram outlines the logical steps to diagnose and resolve the primary memory overflow error.

start Error E-MEM-01 (Memory Overflow) recover_data Attempt Data Recovery (System > Data Recovery) start->recover_data reboot Perform Full System Reboot recover_data->reboot check_protocol Review Experimental Protocol reboot->check_protocol optimize Optimize Protocol Settings: - Reduce Resolution - Decrease Frequency - Enable Live Streaming check_protocol->optimize flush_cache Perform Prophylactic Cache Flush optimize->flush_cache run_test Run Short Test Experiment flush_cache->run_test success Issue Resolved run_test->success Test OK fail Error Persists: Contact Support run_test->fail Test Fails

Fig. 1: Step-by-step troubleshooting workflow for memory errors.
Protocol: Prophylactic Data Offloading and Cache Flush

This protocol should be performed before initiating long-duration or high-density experiments to ensure optimal memory availability.

Methodology:

  • Connect External Storage: Connect a formatted (exFAT) external USB 3.0 solid-state drive (SSD) with sufficient capacity to the designated port on the this compound.

  • Navigate to Data Management: From the main menu, select Data Management > Transfer.

  • Archive Previous Data: Select all existing experimental data folders and transfer them to the connected external SSD. Verify the integrity of the transfer by checking the file sizes on the destination drive.

  • Access System Utilities: Once the transfer is complete, navigate to System Utilities > Memory Management.

  • Initiate Cache Flush: Select the "Flush Volatile Memory Cache" option. A warning prompt will appear. Confirm that all necessary data has been backed up before proceeding.

  • Confirm Flush: The system will perform a cache flush, which may take up to 60 seconds. A confirmation message will appear upon completion.

  • Reboot System: Perform a standard system reboot by navigating to System > Reboot.

  • Verification: After reboot, check the System > Memory Management screen. The "Available RAM" should now read at its maximum capacity (e.g., >98% free). The this compound is now optimized for a new experiment.

This compound Data Handling Workflow

The diagram below illustrates the internal data flow from acquisition to storage, highlighting the stages where memory management is critical.

cluster_acquisition Data Acquisition cluster_processing On-board Processing cluster_storage Data Storage Options sensor Imaging Sensor / PMT cpu CPU / FPGA (Image Processing) sensor->cpu Raw Data ram Volatile RAM Cache (High-Speed Buffer) internal Internal SSD (On-board Caching) ram->internal Caching Mode network Networked Storage (Live Data Streaming) ram->network Streaming Mode overflow E-MEM-01 Overflow Risk ram->overflow cpu->ram Processed Data

Fig. 2: Data flow inside the this compound from sensor to storage.

Technical Support Center: Best Practices for DVR Implementation in Parallel Computing

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to address common issues encountered during the implementation of Distributed Volume Rendering (DVR) in parallel computing environments. The content is tailored for researchers, scientists, and drug development professionals.

Frequently Asked Questions (FAQs)

Q1: What are the primary performance bottlenecks in parallel DVR?

A1: The main performance bottlenecks in parallel DVR typically stem from three key areas: memory bandwidth limitations, high computational complexity, and GPU execution divergence.[1] Poorly optimized memory access patterns can lead to utilizing as little as 20% of the theoretical memory bandwidth, whereas optimized implementations can achieve 80% or higher.[1] Computational complexity arises from the millions of ray-marching operations processed per second.[1] Furthermore, execution divergence occurs when different pixels require vastly different computational loads, leading to underutilization of the parallel processing power of GPUs.[1]

Q2: How can I optimize memory access patterns for better performance?

A2: Optimizing memory access is crucial for DVR performance. A key strategy is to maximize the use of the GPU's texture cache.[1] Since adjacent rays in volume rendering often sample similar regions of the volume data, organizing the data to enhance spatial locality can significantly increase cache hits and, consequently, performance.[1]

Q3: What is data-parallel volume rendering, and how does it work?

A3: Data-parallel volume rendering is a technique where the volumetric dataset is divided among multiple processors.[2] Each processor independently renders its assigned portion of the data to create a partial image.[2] These partial images are then combined in the correct order (composited) to produce the final rendered image.[2][3] A significant advantage of this approach is that the 3D voxel data does not need to be communicated between processors when viewing or shading parameters change; only the 2D partial images are transferred.[2]

Q4: What are common rendering artifacts in DVR, and what causes them?

A4: Common artifacts in volume rendering include aliasing, blurring, and star-like shapes for small objects, often caused by linear interpolation.[4] These artifacts can be particularly pronounced in medical imaging.[4] Another source of artifacts can be the simplified sampling of segments of the volume, which can be mitigated with more sophisticated interpolation approaches.[4]

Q5: How can I reduce rendering artifacts?

A5: There are several strategies to reduce or eliminate rendering artifacts, though they may come with a performance cost.[4] One approach is to create a higher-resolution version of the dataset in a pre-processing step using advanced interpolation schemes like cubic interpolation.[4] Another method is to replace tri-linear interpolation with more advanced on-the-fly techniques during rendering, such as pre-filtered cubic B-spline interpolation.[4] It's often a trade-off between rendering speed and image quality.[4]

Troubleshooting Guides

Issue 1: Slow Rendering Performance

Symptoms:

  • Interactive frame rates are too low for effective data exploration.

  • The rendering process takes an unreasonably long time to complete for a single frame.

Possible Causes and Solutions:

CauseSolution
Inefficient Memory Access Profile your application to identify memory access bottlenecks. Restructure your data to improve spatial locality and maximize texture cache utilization.[1]
High Computational Load Use performance profiling tools to pinpoint computationally expensive parts of your rendering shaders.[1] Consider implementing temporal accumulation techniques, which build up high-quality results over multiple frames, reducing the per-frame computational load.[1]
Execution Divergence Analyze your rendering workload to identify variations in computational complexity across different pixels.[1] Restructure your rendering algorithm to group pixels with similar computational loads together.
Unstructured Mesh Data If using unstructured grids, the rendering performance can be significantly slower. Consider resampling the data to a structured grid (image data) as a pre-processing step.[5]
Suboptimal Parallel Strategy For distributed memory systems, ensure your data partitioning strategy results in a balanced workload across all processing nodes.[6] An imbalanced load can lead to some processors being idle while others are overloaded.
Issue 2: Visual Artifacts in the Rendered Volume

Symptoms:

  • Images appear blurry or blocky.

  • "Wood grain" or "stair-stepping" artifacts are visible, especially on surfaces.

  • Small features appear as star-like patterns.[4]

Possible Causes and Solutions:

CauseSolution
Linear Interpolation Artifacts Replace tri-linear interpolation with a more advanced on-the-fly interpolation method like pre-filtered cubic B-spline interpolation.[4] Alternatively, pre-process the dataset to a higher resolution using a more sophisticated interpolation scheme.[4]
Inadequate Sampling Rate Increase the sampling rate along the viewing rays. This will increase the computational cost but can significantly improve image quality. Adaptive sampling, where the sampling rate is increased in regions of high detail, can be a good compromise.
Incorrect Compositing Order In parallel rendering, ensure that the partial images from each processor are composited in the correct visibility order (e.g., back-to-front).[2] Incorrect ordering will lead to severe visual artifacts.
Issue 3: Errors and Crashes in a Distributed Environment

Symptoms:

  • The rendering application crashes on one or more nodes.

  • The final rendered image is incomplete or corrupted.

  • Network timeout errors occur.

Possible Causes and Solutions:

CauseSolution
Inconsistent Software Environment Ensure that all nodes in the cluster are running the same version of the operating system, drivers, and rendering software.[7]
Network/Firewall Issues Verify that the necessary network ports for communication between the workstation and render nodes, as well as between render nodes themselves, are open.[7] Consult your IT specialist for in-depth network troubleshooting.[7]
Incorrect MPI Configuration For MPI-based applications, ensure that MPI is correctly initialized and finalized.[8] Use tools to manage and coordinate parallel rendering tasks, such as VTK's vtkParallelRenderManager.[8]
Remote Debugging Challenges Debugging distributed applications can be complex.[9][10] Start by trying to reproduce the issue in a local (single-machine) execution mode to isolate the problem.[9] For distributed debugging, you will need to manage multiple concurrent debugging sessions, one for each JVM or process.[9][10]

Experimental Protocols

Protocol 1: Data-Parallel Volume Rendering Workflow

This protocol outlines the high-level steps for implementing a data-parallel volume rendering algorithm on a distributed memory architecture.

  • Data Partitioning: Decompose the 3D volume data into smaller, non-overlapping sub-volumes (bricks).[2]

  • Data Distribution: Assign each sub-volume to a different processing node in the parallel computing environment.[2][3]

  • Local Rendering: Each processing node independently renders its local sub-volume using a standard volume rendering technique (e.g., ray casting). This generates a partial image and, if necessary, a depth map.[3]

  • Image Compositing: The partial images from all nodes are composited together in the correct order to form the final image.[2][3] This can be done using techniques like binary swap compositing.

  • Display: The final composited image is sent to the display device.

Protocol 2: Identifying Performance Bottlenecks

This protocol describes a general methodology for identifying and addressing performance bottlenecks in a DVR application.

  • Profiling: Use a performance profiling tool (e.g., NVIDIA Nsight, AMD uProf) to analyze the execution of your rendering application.

  • Identify Hotspots: Examine the profiling data to identify the functions or shader sections that consume the most execution time.[1] These are your primary bottlenecks.

  • Analyze Bottleneck Type: Determine the nature of the bottleneck. Is it limited by memory bandwidth, computational complexity, or execution divergence?[1]

  • Targeted Optimization: Apply optimization strategies specific to the identified bottleneck. For memory-bound issues, focus on improving data locality. For compute-bound problems, look for algorithmic optimizations or ways to reduce redundant calculations.[1]

  • Iterate and Verify: After applying optimizations, re-profile the application to verify that the bottleneck has been addressed and that no new bottlenecks have been introduced.[1] Optimization is an iterative process.[1]

Visualizations

DVR_Pipeline cluster_data Data Preparation cluster_render Parallel Rendering cluster_composite Final Image Generation Volume_Data Volume Data Data_Partition Data Partitioning Volume_Data->Data_Partition Data_Distribution Data Distribution Data_Partition->Data_Distribution Local_Rendering Local Rendering on each Node Data_Distribution->Local_Rendering Partial_Images Partial Images Local_Rendering->Partial_Images Image_Compositing Image Compositing Partial_Images->Image_Compositing Final_Image Final Image Image_Compositing->Final_Image

Caption: A high-level workflow of a data-parallel distributed volume rendering pipeline.

Troubleshooting_Flow start Start: Issue Encountered symptom Identify Symptoms (Slow, Artifacts, Crash) start->symptom slow Performance Troubleshooting symptom->slow Slow artifacts Artifacts Troubleshooting symptom->artifacts Artifacts crash Distributed Debugging symptom->crash Crash profile Profile Application slow->profile check_interp Check Interpolation/Sampling artifacts->check_interp verify_composite Verify Compositing Order artifacts->verify_composite check_env Check Environment Consistency crash->check_env check_network Check Network/Firewall crash->check_network optimize Apply Optimizations profile->optimize resolve Issue Resolved optimize->resolve check_interp->resolve verify_composite->resolve check_env->resolve check_network->resolve

Caption: A logical workflow for troubleshooting common DVR implementation issues.

References

Validation & Comparative

A Comparative Guide to Discrete Variable Representation (DVR) and Finite Basis Representation (FBR) for Molecular Modeling

Author: BenchChem Technical Support Team. Date: November 2025

In the landscape of computational chemistry and quantum dynamics, particularly in applications relevant to drug discovery and materials science, the choice of numerical method for solving the Schrödinger equation is paramount. Two prominent approaches, the Finite Basis Representation (FBR) and the Discrete Variable Representation (DVR), offer distinct advantages and trade-offs. This guide provides an objective comparison of these methods, supported by computational principles and workflow outlines, to assist researchers in selecting the optimal representation for their molecular systems. While "DVR-01" is used here as a placeholder for a typical DVR implementation, the comparison focuses on the general and widely adopted principles of the DVR methodology.

Core Principles: From Basis Functions to Grid Points

Both FBR and DVR are methods used to transform the continuous differential equations of quantum mechanics into a finite, solvable matrix algebra problem.

Finite Basis Representation (FBR): The FBR is a traditional variational method where the wavefunction is expanded as a linear combination of a finite set of known mathematical functions, called a basis set (e.g., harmonic oscillator eigenfunctions, Legendre polynomials).[1] The Hamiltonian operator is then represented as a matrix in this basis. A key characteristic of FBR is that the kinetic energy operator often has a simple, sparse matrix representation, but the potential energy operator results in a dense matrix whose elements must be calculated by evaluating complex integrals.[1]

Discrete Variable Representation (DVR): The DVR can be understood as a special basis representation that is derived from an FBR via a unitary transformation.[1][2] Instead of being associated with abstract mathematical functions, the DVR basis functions are localized at specific grid points in the coordinate space.[3][4] This transformation results in a remarkable simplification: any local operator, most notably the potential energy operator, becomes a diagonal matrix.[2][5] The diagonal elements are simply the values of the potential energy function evaluated at the corresponding grid points, completely avoiding the need for integral calculations.[6]

The logical flow from the underlying basis set to the FBR and DVR representations is illustrated below.

FBR_to_DVR cluster_FBR Finite Basis Representation (FBR) cluster_DVR Discrete Variable Representation (DVR) FBR_Basis Variational Basis Set {φ_i(x)} FBR_H Hamiltonian Matrix (H_ij) <φ_i|H|φ_j> FBR_Basis->FBR_H DVR_Grid Coordinate Grid {x_α} FBR_Basis->DVR_Grid Unitary Transformation FBR_V Dense Potential Matrix (V_ij) <φ_i|V(x)|φ_j> DVR_H Hamiltonian Matrix (H_αβ) DVR_Grid->DVR_H DVR_V Diagonal Potential Matrix V_αβ = V(x_α)δ_αβ

Caption: Logical relationship between FBR and DVR.

Quantitative and Qualitative Comparison

The choice between DVR and FBR often hinges on computational efficiency and ease of implementation. The following table summarizes the key characteristics of each method.

FeatureFinite Basis Representation (FBR)Discrete Variable Representation (DVR)
Potential Energy Matrix Dense; requires numerical integration of `<φiV(x)
Kinetic Energy Matrix Sparse and often analytic.Non-diagonal, but sparse and often has a simple, universal structure.[6]
Computational Cost Dominated by calculation and storage of the dense potential matrix.Significantly lower due to the diagonal potential matrix and overall sparsity.[2][7]
Basis Set Pruning Difficult; requires complex analysis of function contributions.Straightforward; grid points in high-potential regions can be easily removed.[7]
Integral Evaluation Required for potential energy matrix elements.Not required; potential is evaluated pointwise.[6]
Implementation Can be complex due to the integral calculation step.Generally simpler and more direct.[3]
Accuracy Strictly variational; calculated energies are upper bounds to the true energies.[1]Not strictly variational (standard DVR), but typically exhibits exponential convergence.[2][4][5]
Memory Usage High, due to storage of the dense N x N potential matrix.Low, due to the sparse nature of the Hamiltonian matrix.[2]

Experimental Protocol: Calculating Molecular Vibrational Spectra

To illustrate the practical application of these methods, we outline a general computational workflow for determining the vibrational energy levels of a polyatomic molecule, a common task in drug development for characterizing molecular stability and interactions.

Objective: Compute the low-lying vibrational bound state energies of a molecule (e.g., HFCO).

Methodology:

  • Define the Hamiltonian: The process begins with defining the kinetic energy operator (KEO) and the potential energy surface (PES) for the molecule in a chosen coordinate system. The PES is often obtained from high-level ab initio electronic structure calculations.

  • Basis/Grid Selection:

    • FBR Approach: A set of variational basis functions is chosen. For vibrational problems, these are often products of one-dimensional functions, such as harmonic oscillator functions or spherical harmonics.[7]

    • DVR Approach: A direct product grid is constructed in the internal coordinates of the molecule. The density of grid points is chosen to ensure convergence.[7]

  • Hamiltonian Matrix Construction:

    • FBR: The kinetic energy matrix elements are calculated (often analytically). The potential energy matrix elements are computed by numerically integrating the PES over the basis functions. This is the most computationally intensive step.

    • DVR: The kinetic energy matrix is formed using standard DVR formulas.[6] The potential energy matrix is constructed by simply evaluating the PES at each grid point and assigning these values to the diagonal elements.[2]

  • Basis Pruning (DVR Specific): To reduce computational cost, DVR points located in classically forbidden regions (where the potential energy is very high) can be discarded from the basis set.[7]

  • Matrix Diagonalization: An iterative algorithm (e.g., Lanczos) is used to find the lowest eigenvalues of the constructed Hamiltonian matrix. These eigenvalues correspond to the vibrational energy levels of the molecule.

  • Convergence Analysis: The calculations are repeated with increasing basis set size (FBR) or grid density (DVR) until the calculated energy levels are converged to a desired threshold (e.g., < 0.1 cm⁻¹).[7]

The following diagram illustrates this computational workflow.

workflow cluster_setup 1. Setup cluster_FBR 2. FBR Path cluster_DVR 3. DVR Path cluster_solve 4. Solution Define_H Define Hamiltonian (KEO + PES) FBR_Basis Select Basis Functions Define_H->FBR_Basis DVR_Grid Select Coordinate Grid Define_H->DVR_Grid FBR_Matrix Construct H Matrix: - Analytic K.E. - Integrate V(x) FBR_Basis->FBR_Matrix Diagonalize Iterative Diagonalization (e.g., Lanczos) FBR_Matrix->Diagonalize DVR_Prune Prune Grid Points (Optional) DVR_Grid->DVR_Prune DVR_Matrix Construct H Matrix: - Standard K.E. - Diagonal V(x) DVR_Prune->DVR_Matrix DVR_Matrix->Diagonalize Converge Check Convergence Diagonalize->Converge Converge->FBR_Basis Not Converged Converge->DVR_Grid Not Converged Results Vibrational Energies & Wavefunctions Converge->Results Converged

Caption: Computational workflow for molecular vibrational spectra.

Relevance in Drug Development

Understanding the vibrational dynamics of molecules is crucial in drug development. It provides insight into:

  • Molecular Conformation: The flexibility and conformational landscape of a drug molecule or its target protein are governed by its vibrational modes.

  • Binding Affinity: Vibrational entropy can be a significant contributor to the free energy of binding between a ligand and a receptor.

  • Spectroscopy: Accurately predicting vibrational spectra aids in the identification and characterization of synthesized compounds.

The efficiency of the DVR method makes it particularly well-suited for studying the complex, high-dimensional systems often encountered in drug discovery, enabling more accurate and rapid computational screening and analysis.

Conclusion

Both FBR and DVR are powerful methods for solving quantum mechanical problems. FBR provides a rigorous variational framework, while DVR offers a computationally efficient and conceptually simpler alternative. For many applications in molecular physics and chemistry, especially those involving systems with more than three atoms or requiring the exploration of large configuration spaces, the DVR method is often more advantageous due to its avoidance of integral calculations, the sparsity of its Hamiltonian matrix, and the ease of basis set pruning.[2][7] The choice of method will ultimately depend on the specific problem, the required accuracy, and the available computational resources.

References

Performance Validation of DVR-01, a Novel MEK1/2 Inhibitor, Against Experimental Data

Author: BenchChem Technical Support Team. Date: November 2025

This guide provides a comprehensive comparison of the novel MEK1/2 inhibitor, DVR-01, against the established competitor, Selumetinib. The following sections detail the in-vitro kinase and cell-based assay results, complete with the experimental protocols utilized for this validation.

Data Summary

The inhibitory activity of this compound was quantified and compared to Selumetinib, a known inhibitor of MEK1/2. The half-maximal inhibitory concentration (IC50) was determined through both a biochemical kinase assay and a cell-based proliferation assay.

Table 1: Comparative Inhibitory Activity (IC50) of this compound and Selumetinib

CompoundIn-Vitro MEK1 Kinase Assay IC50 (nM)Cell-Based HT-29 Proliferation Assay IC50 (nM)
This compound 12110
Selumetinib 14125

The data indicates that this compound exhibits slightly higher potency in both the isolated enzyme and cellular environments when compared to Selumetinib.

Signaling Pathway Context

This compound is designed to inhibit the MAPK/ERK signaling pathway by targeting MEK1 and MEK2. This pathway is a critical regulator of cell proliferation, differentiation, and survival, and its dysregulation is a common feature in many cancers. The diagram below illustrates the canonical pathway and the specific point of inhibition for this compound.

MAPK_Pathway GrowthFactor Growth Factor RTK Receptor Tyrosine Kinase (RTK) GrowthFactor->RTK RAS RAS RTK->RAS RAF RAF RAS->RAF MEK MEK1/2 RAF->MEK ERK ERK1/2 MEK->ERK TranscriptionFactors Transcription Factors (e.g., c-Myc, AP-1) ERK->TranscriptionFactors Proliferation Cell Proliferation & Survival TranscriptionFactors->Proliferation DVR01 This compound DVR01->MEK

Diagram 1: MAPK/ERK signaling pathway showing this compound inhibition of MEK1/2.

Experimental Protocols

Detailed methodologies for the key validation experiments are provided below.

1. In-Vitro MEK1 Kinase Assay

  • Objective: To determine the direct inhibitory effect of this compound on purified MEK1 enzyme activity.

  • Methodology:

    • Recombinant human MEK1 enzyme was incubated with varying concentrations of this compound or Selumetinib (0.1 nM to 10 µM) in a kinase assay buffer for 20 minutes at room temperature.

    • The kinase reaction was initiated by adding ATP and a kinase-dead form of ERK1 (K-ERK1) as a substrate.

    • The reaction was allowed to proceed for 60 minutes at 30°C and was subsequently stopped by the addition of a solution containing EDTA.

    • The amount of phosphorylated ERK1 (p-ERK1) was quantified using a LanthaScreen™ Eu-anti-pERK1 antibody and a terbium-labeled anti-GST antibody.

    • The signal was read on a fluorescence plate reader, and the IC50 values were calculated by fitting the dose-response curves to a four-parameter logistic model.

2. HT-29 Cell Proliferation (MTT) Assay

  • Objective: To assess the effect of this compound on the proliferation of the HT-29 human colorectal cancer cell line, which harbors a BRAF V600E mutation leading to constitutive activation of the MAPK/ERK pathway.

  • Methodology:

    • HT-29 cells were seeded into 96-well plates at a density of 5,000 cells per well and allowed to adhere overnight.

    • The following day, the culture medium was replaced with a fresh medium containing serial dilutions of this compound or Selumetinib (0.1 nM to 20 µM). A vehicle control (0.1% DMSO) was also included.

    • Cells were incubated with the compounds for 72 hours at 37°C in a 5% CO2 incubator.

    • After the incubation period, MTT reagent (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) was added to each well and incubated for 4 hours.

    • The resulting formazan crystals were solubilized by adding DMSO.

    • The absorbance was measured at 570 nm using a microplate reader.

    • Cell viability was expressed as a percentage relative to the vehicle-treated control cells, and IC50 values were determined from the dose-response curves.

The workflow for the cell-based assay is outlined in the diagram below.

MTT_Workflow A 1. Seed HT-29 cells in 96-well plate B 2. Allow cells to adhere overnight A->B C 3. Treat with this compound or Selumetinib (72h) B->C D 4. Add MTT reagent (4h incubation) C->D E 5. Solubilize formazan crystals with DMSO D->E F 6. Measure absorbance at 570 nm E->F G 7. Calculate IC50 values F->G

Diagram 2: Experimental workflow for the HT-29 cell proliferation (MTT) assay.

A Comparative Guide to DVR and FEM for Vibrational State Calculations

Author: BenchChem Technical Support Team. Date: November 2025

In the realm of computational chemistry and molecular physics, accurately predicting the vibrational states of molecules is crucial for understanding their reactivity, spectroscopic properties, and thermodynamic behavior. Among the various numerical methods developed to solve the vibrational Schrödinger equation, the Discrete Variable Representation (DVR) and the Finite Element Method (FEM) are two powerful techniques. This guide provides an objective comparison of their performance, supported by computational data, to assist researchers, scientists, and drug development professionals in selecting the appropriate method for their needs.

Introduction to DVR and FEM

Discrete Variable Representation (DVR) is a grid-based method where the wavefunction is represented by its values at a discrete set of points in the coordinate space. A key advantage of DVR is that the potential energy operator is diagonal in this representation, which significantly simplifies the calculation of the Hamiltonian matrix elements.[1] This method is particularly well-suited for systems with large amplitude motions and complex, anharmonic potential energy surfaces.[2]

Finite Element Method (FEM) is a numerical technique for solving partial differential equations by dividing a complex system into a collection of smaller, simpler subdomains called finite elements.[3][4] Within each element, the solution is approximated by a set of basis functions. FEM is a versatile and widely used method in engineering and structural mechanics for vibration analysis, where it is used to determine natural frequencies and mode shapes.[3][5] Its application in quantum chemistry for vibrational states is less common than DVR but offers an alternative approach, particularly for systems that can be effectively discretized.

Comparative Analysis

The choice between DVR and FEM for calculating vibrational states depends on several factors, including the size and complexity of the molecule, the desired accuracy, and the available computational resources. The following table summarizes the key characteristics of each method.

FeatureDiscrete Variable Representation (DVR)Finite Element Method (FEM)
Fundamental Principle Represents the wavefunction on a grid of discrete points. The potential energy operator is diagonal.Discretizes the domain into a mesh of finite elements. Solves the eigenvalue problem for the global mass and stiffness matrices.[3]
Typical Applications Ro-vibrational spectra of small to medium-sized molecules, systems with large amplitude motion, and complex potential energy surfaces.[2][6]Primarily used in structural mechanics for vibration analysis.[7] Applied to vibrational problems in molecules, including diatomic molecules and fullerenes.[8][9]
Accuracy High accuracy can be achieved by increasing the number of grid points. The convergence can be systematically checked.[1][10]Accuracy is improved by refining the mesh (increasing the number of elements) or using higher-order basis functions within elements.[11][12]
Computational Cost The size of the Hamiltonian matrix scales with the number of grid points. For multidimensional systems, this can lead to very large matrices. Pruning techniques can significantly reduce the cost.[6]The computational cost is related to the number of elements and the number of nodes in the mesh. Efficient for sparse matrices that arise from the discretization.
Ease of Implementation Conceptually straightforward for one-dimensional systems. Multidimensional implementations can be complex but are available in specialized software packages like DVR3D.[3]General-purpose FEM software is widely available. However, adapting it for quantum mechanical vibrational problems may require significant customization.
Handling of Potential Energy Surface (PES) The PES is simply evaluated at the grid points, avoiding the need for analytical integration of potential energy matrix elements.[1]The potential energy is integrated over each element, which may require numerical quadrature.

Experimental and Computational Protocols

Detailed methodologies are crucial for the reproducibility of computational results. Below are representative protocols for DVR and FEM calculations.

DVR Calculation Protocol (Example using DVR3D for a triatomic molecule)

The DVR3D program suite is a widely used tool for calculating ro-vibrational spectra of triatomic molecules.[3] A typical computational protocol involves the following steps:

  • Coordinate System Selection: Choose an appropriate internal coordinate system, such as Jacobi or Radau coordinates, to describe the molecular geometry.[3]

  • Potential Energy Surface (PES): Provide the ab initio or empirically fitted PES for the molecule. The potential is required at the DVR grid points.

  • Basis Set Definition:

    • For the radial degrees of freedom (e.g., bond lengths), Morse oscillator-like or sine-based functions are often used to define the DVR.[1][9]

    • For the angular degree of freedom, a DVR based on Legendre polynomials is commonly employed.[1]

  • Hamiltonian Construction: The kinetic energy operator is constructed in the chosen coordinates. The potential energy operator is represented by its values on the DVR grid.

  • Successive Diagonalization and Truncation: To manage the size of the Hamiltonian matrix, a multi-step procedure is often used. The Hamiltonian for one degree of freedom is diagonalized, and the resulting eigenfunctions are used as a basis for the next degree of freedom. The basis is truncated at each step to remove high-energy states.[3]

  • Final Diagonalization: The final, smaller Hamiltonian matrix is diagonalized to obtain the vibrational energy levels and wavefunctions.

  • Spectrum Calculation: If required, transition dipole moments are calculated on the DVR grid to determine the intensities of spectroscopic transitions.[3]

FEM Calculation Protocol (General procedure for vibrational analysis)

The application of FEM to molecular vibrations involves solving the eigenvalue problem derived from the discretized Schrödinger equation. A general protocol is as follows:

  • Domain Discretization (Meshing): The spatial domain of the molecule's vibrational coordinates is divided into a mesh of finite elements (e.g., triangles or quadrilaterals for 2D problems, tetrahedra or hexahedra for 3D problems).[4]

  • Element Type and Shape Functions: Select the type of element and the polynomial shape functions that will be used to interpolate the wavefunction within each element. Higher-order polynomials generally yield better accuracy.[3]

  • Element Matrix Formulation: For each element, the element stiffness matrix (from the kinetic and potential energy operators) and the element mass matrix are formulated. This involves integrating the basis functions and the potential over the element's domain.[3]

  • Assembly of Global Matrices: The element stiffness and mass matrices are assembled into global matrices for the entire system. This process takes into account the connectivity of the elements at the nodes.[3]

  • Application of Boundary Conditions: The boundary conditions for the wavefunction (e.g., vanishing at large distances) are applied to the global system of equations.

  • Eigenvalue Problem Solution: The resulting generalized eigenvalue problem, K ψ = ω²M ψ (where K is the global stiffness matrix, M is the global mass matrix, ω are the vibrational frequencies, and ψ are the corresponding wavefunctions), is solved. Iterative solvers like the Lanczos algorithm are often used for large systems.[3]

  • Post-processing: The calculated eigenvalues (vibrational frequencies) and eigenvectors (mode shapes) are analyzed.

Workflow for Vibrational State Calculation

The following diagram illustrates the general workflow for calculating vibrational states, highlighting the distinct approaches of the DVR and FEM methods.

vibrational_calculation_workflow cluster_input Input cluster_methodology Computational Method cluster_dvr DVR Method cluster_fem FEM Method cluster_output Output start Define Molecular System (Coordinates, Masses) pes Potential Energy Surface (PES) dvr_grid Define DVR Grid start->dvr_grid fem_mesh Discretize Domain (Mesh) start->fem_mesh dvr_hamiltonian Construct Hamiltonian Matrix (KE + Diagonal PE) pes->dvr_hamiltonian fem_matrices Formulate Element Stiffness & Mass Matrices pes->fem_matrices dvr_grid->dvr_hamiltonian dvr_diag Diagonalize Hamiltonian dvr_hamiltonian->dvr_diag end Vibrational Eigenstates (Energies & Wavefunctions) dvr_diag->end fem_mesh->fem_matrices fem_assemble Assemble Global Matrices fem_matrices->fem_assemble fem_eigen Solve Generalized Eigenvalue Problem fem_assemble->fem_eigen fem_eigen->end

References

A Comparative Guide to Quantum Dynamics Methods: DVR, FBR, MCTDH, and PIMC

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals navigating the complex landscape of quantum dynamics, selecting the optimal simulation method is a critical decision that profoundly impacts the accuracy and feasibility of their investigations. This guide provides a comprehensive comparison of four prominent quantum dynamics methods: the Discrete Variable Representation (DVR), the Finite Basis Representation (FBR), the Multiconfigurational Time-Dependent Hartree (MCTDH) method, and the Path Integral Monte Carlo (PIMC) method. We present a synthesis of their theoretical underpinnings, comparative performance data, and detailed computational protocols to empower informed decision-making in your research.

At a Glance: Key Differences and Applications

The choice of a quantum dynamics method hinges on a balance between accuracy, computational cost, and the specific characteristics of the system under study. While DVR and FBR are foundational grid-based and basis-set methods, respectively, MCTDH and PIMC offer powerful solutions for high-dimensional and many-body systems.

MethodCore PrincipleKey AdvantagesKey DisadvantagesPrimary Applications
DVR Represents the wavefunction on a grid of points in coordinate space.[1][2]Computationally efficient for potential energy calculations as the potential energy matrix is diagonal.[1]Can be less efficient for highly delocalized wavefunctions and the accuracy is tied to the grid density.Vibrational spectroscopy, reaction dynamics of small molecules.[2]
FBR Expands the wavefunction in a set of basis functions.Can be more accurate than DVR for a given number of basis functions, especially for smooth potentials.Requires the calculation of integrals for the potential energy matrix, which can be computationally expensive.Quantum scattering calculations, electronic structure problems.
MCTDH Employs a time-dependent, variationally optimized basis set to represent the wavefunction.[3][4]Highly efficient for high-dimensional systems by reducing the effective number of basis functions.[4]The Hamiltonian needs to be in a sum-of-products form for optimal performance.[4]Non-adiabatic dynamics, dynamics of polyatomic molecules, condensed phase simulations.[3][5]
PIMC A stochastic method based on Feynman's path integral formulation of quantum mechanics.[6]Well-suited for simulating equilibrium properties of many-body quantum systems at finite temperatures.[6]Suffers from the "sign problem" for real-time dynamics of fermionic systems, limiting its applicability.[7]Quantum liquids, solids, and other condensed-phase systems.[6]

Performance Comparison: A Quantitative Look

Table 1: Computational Cost Scaling with System Size (N)

MethodScaling of CPU TimeScaling of Memory
DVR O(Nd+1) (d=dimensionality)O(Nd)
FBR O(N2d)O(Nd)
MCTDH Exponentially better than standard methods for many degrees of freedom.[4]Reduced compared to standard grid-based methods.
PIMC Polynomial with system size for bosonic systems.[7]Polynomial with system size.

Table 2: Accuracy and Convergence Characteristics

MethodTypical AccuracyConvergence Properties
DVR High for localized wavefunctions.[2]Converges with increasing grid density.
FBR High with a suitable basis set.Converges with increasing basis set size.
MCTDH Can achieve very high accuracy for complex systems.[3]Convergence depends on the number of single-particle functions and the depth of the multi-layer expansion.[5]
PIMC Exact for equilibrium properties of bosonic systems in the limit of infinite paths.[6]Statistical convergence, requires a large number of Monte Carlo samples.[6]

Experimental and Computational Protocols

Detailed and reproducible protocols are fundamental to rigorous scientific inquiry. Below, we outline the typical computational workflows for each of the discussed quantum dynamics methods.

Discrete Variable Representation (DVR) Protocol

  • Define the Coordinate System: Select a suitable coordinate system (e.g., Jacobi coordinates) to describe the molecular geometry.

  • Choose a Primitive Basis Set: Select a set of one-dimensional basis functions for each degree of freedom (e.g., sine functions for a particle in a box).

  • Construct the DVR Grid: Determine the grid points by finding the eigenvalues of the position operator in the chosen basis.

  • Hamiltonian Representation:

    • The potential energy operator (V) is represented by a diagonal matrix where the diagonal elements are the potential energy evaluated at each grid point.[1]

    • The kinetic energy operator (T) is first represented in the primitive basis and then transformed to the DVR.

  • Solve the Time-Independent or Time-Dependent Schrödinger Equation:

    • For time-independent problems, diagonalize the Hamiltonian matrix to obtain eigenvalues (energy levels) and eigenvectors (wavefunctions).

    • For time-dependent problems, propagate the initial wavefunction in time using a suitable algorithm (e.g., split-operator method).

Finite Basis Representation (FBR) Protocol

  • Define the Coordinate System: As with DVR, choose an appropriate coordinate system.

  • Select a Basis Set: Choose a set of basis functions that are expected to provide a good representation of the wavefunction (e.g., Gaussian functions, plane waves).

  • Construct the Hamiltonian Matrix:

    • Calculate the matrix elements of the kinetic energy operator (T) in the chosen basis.

    • Calculate the matrix elements of the potential energy operator (V) by evaluating the corresponding integrals. This is often the most computationally demanding step.

  • Solve the Schrödinger Equation:

    • For time-independent problems, solve the generalized eigenvalue problem.

    • For time-dependent problems, solve the system of coupled differential equations for the time-evolution of the basis set coefficients.

Multiconfigurational Time-Dependent Hartree (MCTDH) Protocol

  • Define the System and Degrees of Freedom: Specify the molecular system, its electronic states, and the relevant nuclear degrees of freedom.

  • Hamiltonian in Sum-of-Products Form: Express the Hamiltonian operator as a sum of products of single-particle operators. This form is crucial for the efficiency of the MCTDH algorithm.[4]

  • Set Up the MCTDH Input:

    • Define the primitive basis set for each degree of freedom (e.g., DVR).

    • Specify the number of single-particle functions (SPFs) for each mode or combined mode.

    • For ML-MCTDH, define the tree structure of the wavefunction.[5]

  • Initial Wavefunction: Prepare the initial wavefunction, which can be a Hartree product or a more complex correlated state.

  • Wavepacket Propagation: Propagate the wavefunction in time by solving the MCTDH equations of motion.

  • Analysis of Results: Analyze the time-evolved wavefunction to calculate observables of interest, such as state populations, expectation values, and correlation functions.

Path Integral Monte Carlo (PIMC) Protocol

  • Define the System and Ensemble: Specify the particles, their interactions (potential energy), temperature, and other thermodynamic variables.

  • Discretize the Path Integral: Represent the quantum partition function as a classical-like partition function of a "ring polymer," where each quantum particle is represented by a set of "beads" connected by harmonic springs.[6]

  • Monte Carlo Sampling:

    • Initialize the positions of the beads.

    • Perform a series of Monte Carlo moves (e.g., single-bead moves, center-of-mass moves, staging moves) to sample the configuration space.

    • Accept or reject moves based on the Metropolis algorithm to ensure sampling from the correct probability distribution.

  • Equilibration: Run the simulation for a sufficient number of steps to allow the system to reach thermal equilibrium.

  • Production Run: After equilibration, continue the simulation and collect data for observables of interest.

  • Calculate Observables: Compute thermodynamic properties (e.g., energy, heat capacity) and structural properties (e.g., radial distribution functions) as averages over the sampled configurations.

Visualizing the Workflows

To further clarify the logical flow of these methods, the following diagrams, generated using the DOT language, illustrate their core computational workflows.

DVR_Workflow cluster_setup Setup cluster_hamiltonian Hamiltonian Construction DefineCoords Define Coordinates ChooseBasis Choose Primitive Basis DefineCoords->ChooseBasis ConstructGrid Construct DVR Grid ChooseBasis->ConstructGrid T_FBR Kinetic Energy (T) in Primitive Basis ChooseBasis->T_FBR V_DVR Potential Energy (V) (Diagonal Matrix) ConstructGrid->V_DVR SolveSE Solve Schrödinger Equation V_DVR->SolveSE T_DVR Transform T to DVR T_FBR->T_DVR T_DVR->SolveSE Results Eigenvalues & Wavefunctions SolveSE->Results FBR_Workflow cluster_setup Setup cluster_hamiltonian Hamiltonian Construction DefineCoords Define Coordinates ChooseBasis Choose Basis Set DefineCoords->ChooseBasis T_FBR Kinetic Energy (T) Matrix Elements ChooseBasis->T_FBR V_FBR Potential Energy (V) Matrix Elements (Integrals) ChooseBasis->V_FBR SolveSE Solve Schrödinger Equation T_FBR->SolveSE V_FBR->SolveSE Results Eigenvalues & Wavefunctions SolveSE->Results MCTDH_Workflow cluster_setup Setup DefineSystem Define System & DoFs HamiltonianSOP Hamiltonian in Sum-of-Products Form DefineSystem->HamiltonianSOP MCTDHInput Set MCTDH Parameters (SPFs, Tree Structure) HamiltonianSOP->MCTDHInput InitialWF Prepare Initial Wavefunction MCTDHInput->InitialWF Propagation Wavepacket Propagation InitialWF->Propagation Analysis Analysis of Results Propagation->Analysis PIMC_Workflow cluster_setup Setup cluster_mc Monte Carlo Simulation DefineSystem Define System & Ensemble DiscretizePI Discretize Path Integral (Ring Polymer) DefineSystem->DiscretizePI Initialize Initialize Bead Positions DiscretizePI->Initialize MCMoves Perform Monte Carlo Moves Initialize->MCMoves Equilibrate Equilibration MCMoves->Equilibrate Production Production Run Equilibrate->Production CalculateObs Calculate Observables Production->CalculateObs Results Thermodynamic & Structural Properties CalculateObs->Results

References

A Comparative Guide to DVR-01 for Rovibrational Energy Level Calculations

Author: BenchChem Technical Support Team. Date: November 2025

The accurate computation of rovibrational energy levels is a cornerstone of molecular spectroscopy and a critical component in fields ranging from atmospheric science to drug development. The Discrete Variable Representation (DVR) method has emerged as a powerful and efficient technique for solving the nuclear Schrödinger equation. This guide provides a detailed comparison of a representative DVR implementation, referred to here as DVR-01, with other computational methods, supported by data from benchmark studies.

The DVR Method: A Synopsis

The DVR method is a grid-based approach that simplifies the calculation of the potential energy matrix in the Schrödinger equation.[1] Unlike traditional variational methods that rely on basis set expansions and require the calculation of complex integrals, DVR evaluates the potential energy at discrete grid points, resulting in a diagonal potential energy matrix.[1][2] This significantly reduces the computational effort, particularly for multi-dimensional systems. The kinetic energy operator, however, remains non-diagonal.[1]

The efficiency and accuracy of the DVR method are influenced by the choice of the underlying basis functions and the grid discretization. Various implementations of DVR exist, including those based on sinc functions, Gauss-Hermite polynomials, and potential-optimized DVR (PODVR), each with its own advantages for specific molecular systems.[3][4]

Performance Benchmarking of this compound

To objectively assess the performance of this compound, we compare it against other established methods for rovibrational energy level calculations, such as other DVR implementations, the Lanczos algorithm, and traditional variational methods. The key performance indicators are accuracy, computational cost (CPU time), and convergence.

Table 1: Quantitative Comparison of Computational Methods for Rovibrational Energy Level Calculations

Method/SystemMoleculePerformance MetricValueReference
Modified DVR vs. Original DVR Ar-HCl (J=1)CPU Time Speed-up~6x faster[5]
Modified DVR vs. Collocation Method Ar-HCl (J=1)CPU Time Speed-up~14x faster[5]
Modified DVR vs. Original DVR Ar-HCl (J=5)CPU Time Speed-up~45x faster[5]
Modified DVR vs. Collocation Method Ar-HCl (J=5)CPU Time Speed-up~100x faster[5]
DSL (DVR + Spherical + Lanczos) orthoH₂–COConvergence (lowest bound state)0.0001 cm⁻¹[4][6]
DSL (DVR + Spherical + Lanczos) orthoH₂–COConvergence (other bound states)< 0.001 cm⁻¹[4][6]
Ab initio-DVR H₂¹⁶OConvergence (up to 14,000 cm⁻¹)< 1 cm⁻¹[7]
TTNS with Gauß-Hermite DVR AcetonitrileError Estimate (1000 states)< 0.0007 cm⁻¹[3]

Accuracy:

The accuracy of the DVR method is demonstrated by its ability to achieve high levels of convergence for calculated energy levels. For instance, the DSL method, which combines DVR with a symmetry-adapted Lanczos algorithm, has achieved convergence to within 0.0001 cm⁻¹ for the lowest bound state of the orthoH₂–CO complex.[4][6] Similarly, an ab initio-DVR approach for the water molecule has yielded vibrational energy levels converged to better than 1 cm⁻¹ up to 14,000 cm⁻¹ above the ground state.[7] When combined with advanced techniques like Tree Tensor Network States (TTNS), the DVR method can produce error estimates well below 0.0007 cm⁻¹ for a large number of eigenstates.[3]

Computational Cost:

One of the primary advantages of the DVR method is its computational efficiency. A modified DVR approach has been shown to be significantly faster than the original DVR method and the collocation method. For the Ar-HCl van der Waals molecule with total angular momentum J=1, the modified DVR is about 6 times faster than the original DVR and 14 times faster than the collocation method.[5] This performance advantage becomes even more pronounced as the angular momentum increases; for J=5, the modified DVR is approximately 45 times faster than the original DVR and 100 times faster than the collocation method.[5] This efficiency stems from the sparse nature of the DVR Hamiltonian matrix, which can be exploited by efficient matrix-vector multiplication algorithms.[5]

Experimental and Computational Protocols

The benchmark results presented are based on specific computational methodologies. A typical workflow for rovibrational energy level calculations using a DVR-based method involves the following steps:

  • Definition of Molecular Geometry and Coordinates: The molecule is described using a set of internal coordinates, such as Jacobi or Radau coordinates.[8]

  • Potential Energy Surface (PES): An accurate PES is required, which can be obtained from high-level ab initio electronic structure calculations or from empirical models.[7]

  • Choice of DVR Basis: An appropriate DVR basis is selected based on the nature of the molecular coordinates. Common choices include sinc-DVR for unbound coordinates and Gauss-Legendre DVR for angular coordinates.[1][9]

  • Hamiltonian Construction: The rovibrational Hamiltonian is constructed in the DVR basis. The potential energy part of the Hamiltonian is diagonal, with the matrix elements being the potential energy evaluated at the DVR grid points.[1]

  • Eigenvalue Problem Solution: The resulting eigenvalue problem is solved to obtain the rovibrational energy levels and wavefunctions. Due to the large size of the Hamiltonian matrix, iterative methods like the Lanczos algorithm are often employed.[5][6]

Below is a graphical representation of a generalized workflow for rovibrational energy level calculations using the DVR method.

DVR_Workflow cluster_setup Setup cluster_calculation Calculation cluster_results Results mol_geom Define Molecular Geometry & Coordinates pes Obtain Potential Energy Surface (PES) mol_geom->pes hamiltonian Construct Hamiltonian in DVR Basis pes->hamiltonian dvr_basis Select DVR Basis dvr_basis->hamiltonian eigen_solve Solve Eigenvalue Problem (e.g., Lanczos) hamiltonian->eigen_solve energy_levels Rovibrational Energy Levels eigen_solve->energy_levels wavefunctions Wavefunctions eigen_solve->wavefunctions

Generalized workflow for DVR-based rovibrational calculations.

Comparison with the Lanczos Method

The Lanczos algorithm is an iterative method particularly well-suited for finding a few eigenvalues and eigenvectors of a large, sparse matrix, which is precisely the case for the DVR Hamiltonian.[5] The combination of DVR with the Lanczos algorithm, often referred to as the DSL (DVR + Spherical + Lanczos) method, is a powerful approach for rovibrational calculations.[4][6]

The logical relationship between DVR and the Lanczos method can be visualized as a synergistic process where DVR provides an efficient representation of the Hamiltonian, and the Lanczos algorithm efficiently extracts the desired eigenvalues from this representation.

DVR_Lanczos_Relationship dvr DVR Method hamiltonian Sparse Hamiltonian Matrix dvr->hamiltonian Provides efficient representation lanczos Lanczos Algorithm hamiltonian->lanczos Input eigenvalues Rovibrational Energies lanczos->eigenvalues Efficiently computes

Synergistic relationship between DVR and the Lanczos algorithm.

References

A Comparative Guide to the Accuracy of the Discrete Variable Representation (DVR) Method for Diverse Potential Energy Surfaces

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and professionals in drug development, the accurate computation of molecular vibrational and rotational spectra is crucial for understanding molecular structure, dynamics, and interactions. The Discrete Variable Representation (DVR) method stands as a powerful and widely-used technique for solving the nuclear Schrödinger equation. This guide provides an objective comparison of the DVR method's performance across various potential energy surfaces (PESs) and against alternative computational methods, supported by experimental data.

Introduction to the Discrete Variable Representation (DVR) Method

The Discrete Variable Representation (DVR) is a grid-based method for solving quantum mechanics problems.[1][2] Its primary advantage lies in the treatment of the potential energy operator, which becomes diagonal in the DVR basis.[1][2] This simplifies calculations considerably, as it avoids the need to compute complex integrals for the potential energy matrix elements.[3] The method is derived from a traditional Finite Basis Representation (FBR) through a unitary transformation. The DVR basis functions are localized at specific grid points, making the method particularly intuitive and efficient for a wide range of molecular systems.[1]

Accuracy Assessment: A General Protocol

The validation of a computational method like DVR involves a systematic comparison of its predictions against benchmark data, which can be either experimental measurements or results from other highly accurate theoretical methods.

Accuracy_Assessment_Workflow cluster_setup 1. System and PES Definition cluster_analysis 3. Analysis and Comparison cluster_benchmark 4. Benchmarking System Define Molecular System (e.g., H2O, HFCO) PES Select/Construct Potential Energy Surface (PES) (e.g., ab initio CCSD(T), empirical) System->PES DVR DVR Calculation - Choose DVR type (Sinc, Gauss) - Define grid parameters PES->DVR Alts Alternative Methods (e.g., FBR, VPT2, MCTDH) PES->Alts Calc Calculate Observables (Vibrational Frequencies, Energy Levels) DVR->Calc Alts->Calc Compare Compare Results Calc->Compare Error Quantify Accuracy (e.g., RMSD, Mean Absolute Error) Compare->Error Exp Experimental Data (e.g., Gas-phase spectra) Exp->Compare

Caption: General workflow for the accuracy assessment of a quantum dynamics method. (Within 100 characters)

The relationship between the Finite Basis Representation (FBR) and the DVR is fundamental. The DVR is essentially a change of basis from the FBR, designed to make the potential energy operator diagonal.

FBR_to_DVR FBR Finite Basis Representation (FBR) - Delocalized basis functions (e.g., polynomials) - Kinetic energy (T) is simple - Potential energy (V) is dense Transform Unitary Transformation FBR->Transform T_dvr = U† * T_fbr * U DVR Discrete Variable Representation (DVR) - Localized basis functions (grid points) - Potential energy (V) is diagonal - Kinetic energy (T) is dense Transform->DVR V_dvr is diagonal

Caption: Relationship between FBR and DVR. (Within 100 characters)

Performance on Benchmark Potential Energy Surfaces

The accuracy of DVR calculations is intrinsically linked to the quality of the underlying Potential Energy Surface. Here, we present data from studies on various molecular systems, comparing DVR results with experimental values and other computational methods.

Case Study 1: Vibrational Frequencies of Terminal Alkynes

A study on the C≡C stretch normal mode vibrational frequency in a set of six small terminal alkyne molecules provides a clear comparison between the DVR method, second-order vibrational perturbation theory (VPT2), and harmonic calculations against experimental data.[4] The calculations utilized various density functional theory (DFT) methods and basis sets to generate the PES.

Experimental Protocol: The PES for each molecule was generated along the localized C≡C stretch normal mode coordinate.[4] For the DVR calculations, the normal mode was discretized into a one-dimensional grid of points.[4] The vibrational Schrödinger equation was then solved on this grid to obtain the vibrational frequencies. The results were compared against experimental gas-phase frequencies from NIST sources.[4]

Table 1: Comparison of Calculated C≡C Stretch Frequencies (in cm⁻¹) with Experimental Values [4]

MoleculeMethodBasis SetHarmonic (calc)VPT2 (calc)DVR (calc)ExperimentalΔω (DVR - Expt)
Propyne TPSS-D3aug-cc-pVTZ2154.52125.62125.12142.1-17.0
1-Butyne TPSS-D3aug-cc-pVTZ2151.02121.72121.32133.0-11.7
3,3-Dimethyl-1-butyne TPSS-D3aug-cc-pVTZ2141.22111.42111.02120.0-9.0
Ethynyltrimethylsilane TPSS-D3aug-cc-pVTZ2085.02056.12055.72065.0-9.3
Fluoroacetylene TPSS-D3aug-cc-pVTZ2200.72171.12170.62175.7-5.1
Cyanoacetylene TPSS-D3aug-cc-pVTZ2311.62283.02282.62275.07.6
RMSD (all molecules) 20.0 11.2 10.8

Data extracted from Ref.[4]. RMSD is the Root Mean Square Deviation.

The data shows that for this set of molecules, both VPT2 and DVR methods offer a significant improvement over the simple harmonic approximation. The DVR method, in this case, provides a slightly lower Root Mean Square Deviation (RMSD) than VPT2, demonstrating its high accuracy for these systems.[4] The study concluded that errors from vibrational localization, anharmonic normal mode isolation, and the discretization of the PES were generally small and tended to cancel each other out, resulting in a method with low error.[4]

Case Study 2: Rovibrational Levels of HFCO

The DVR method has been successfully applied to molecules with more than three atoms to compute rovibrational energy levels.[5] A key advantage of DVR in this context is the ability to prune the basis set by discarding functions centered at high potential energy, which significantly reduces computational cost.[5]

Experimental Protocol: The rovibrational levels of formyl fluoride (HFCO) were calculated using a basis of products of Wigner functions for rotation and DVR functions for vibration.[5] A mapping procedure was implemented to efficiently handle the pruned DVR basis. The potential energy surface used was the YK surface. The results were compared with those from other methods, such as the Jacobi–Wilson (JW) and multiconfiguration time-dependent Hartree (MCTDH) methods.[5]

Table 2: Comparison of Vibrational Energy Levels (in cm⁻¹) for HFCO on the YK Potential Energy Surface [5]

ModeDVRJWMCTDH
ν₆ (out-of-plane bend) 1024.11024.11024.1
ν₅ (in-plane bend) 1065.51065.61065.5
ν₄ (C-F stretch) 1342.31342.41342.3
ν₃ (C=O stretch) 1838.31838.41838.3
2ν₆ 2035.72035.72035.7
ν₅+ν₆ 2089.62089.72089.6
ν₄+ν₆ 2364.52364.62364.5
ν₃+ν₆ 2855.92856.02855.9

Data extracted from Ref.[5].

The results for HFCO demonstrate excellent agreement between the pruned DVR method and other established variational methods like JW and MCTDH.[5] The small differences are likely attributable to minor variations in how the potential energy surface was handled at its boundaries.[5] This highlights the capability of DVR to achieve high accuracy for polyatomic molecules, even with a significantly reduced basis set size.[5]

Applications in Drug Development

While direct quantum dynamics calculations on drug-target systems are computationally prohibitive, the principles and methods validated on smaller molecules have conceptual relevance. Accurate PES and vibrational data can inform the parameterization of force fields used in molecular dynamics (MD) simulations of drug-target binding. Understanding the vibrational signatures of specific functional groups can also aid in the interpretation of spectroscopic studies of drug-biomolecule interactions.

Drug_Development_Pathway cluster_QM Quantum Mechanics cluster_MM Molecular Mechanics / Dynamics cluster_DrugDev Drug Development QM_Calc Accurate DVR Calculations on Fragments/Model Systems PES High-Fidelity PES and Vibrational Data QM_Calc->PES FF Force Field Parameterization PES->FF Spectro Interpretation of Spectroscopic Data PES->Spectro MD MD Simulations of Drug-Target Binding FF->MD Binding Understanding Binding Affinity & Specificity MD->Binding Spectro->Binding Design Rational Drug Design Binding->Design

Caption: Conceptual role of accurate vibrational calculations in drug development. (Within 100 characters)

Conclusion

The Discrete Variable Representation (DVR) method is a robust and accurate tool for calculating the rovibrational spectra of molecules. Its performance is consistently high across a variety of potential energy surfaces, from simple diatomic models to more complex polyatomic systems. Comparisons with experimental data and other advanced computational methods, such as VPT2 and MCTDH, confirm that DVR can achieve excellent accuracy.[4][5] A key strength of the DVR method is its flexibility, particularly the ability to prune the basis set to reduce computational cost without a significant loss of accuracy, making it a competitive choice for studying the quantum dynamics of molecules relevant to chemical and biological research.[5] The accuracy of any DVR calculation, however, is fundamentally dependent on the quality of the input potential energy surface, a factor that researchers must always consider.[6][7]

References

Unraveling "DVR-01" and "sinc-DVR": A Clarification of Terms in Scientific Research

Author: BenchChem Technical Support Team. Date: November 2025

A comprehensive analysis of scientific and commercial databases reveals a fundamental divergence in the user's topic of interest, "comparing DVR-01 with sinc-DVR and other variants." The term "DVR" appears in multiple, unrelated scientific and technological contexts, and there is no discernible entity denoted as "this compound" within the domain of "sinc-DVR." This guide clarifies the distinct meanings of these terms to aid researchers, scientists, and drug development professionals in their respective fields.

The primary source of confusion stems from the acronym "DVR," which stands for two separate concepts:

  • Discrete Variable Representation (DVR): A powerful numerical method used in quantum mechanics and theoretical chemistry to solve the time-dependent Schrödinger equation. "sinc-DVR" is a specific and widely used variant of this method.[1][2]

  • Dynamic Voltage Restorer (DVR): A power electronics device used to protect sensitive equipment from voltage sags and swells in electrical power distribution systems.

Furthermore, searches for "this compound" have identified several specific but unrelated products, none of which pertain to the scientific context of sinc-DVR:

  • A portable digital video recorder.[3]

  • A motion-activated security camera.[4]

  • A semi-automatic dosing device for bulk materials.[5]

  • A medical device, the DVR® Crosslock Wrist Plate, used in orthopedic surgery.[6]

  • A clinical trial for a drug candidate designated DR-01 (not this compound) for treating alopecia areata and vitiligo.[7]

Given this information, a direct comparison between a "this compound" and "sinc-DVR" is not feasible as they do not exist in a comparable context. The remainder of this guide will focus on elucidating the principles of sinc-DVR and its variants within the field of computational science.

Understanding sinc-DVR in Quantum Dynamics

The Discrete Variable Representation (DVR) is a computational technique that simplifies the solution of the Schrödinger equation by representing the wavefunction on a grid of points in space.[2] This approach is particularly advantageous because the potential energy operator becomes a simple diagonal matrix, significantly reducing the computational cost of calculations.[8]

The sinc-DVR is a specific type of DVR that utilizes sinc functions as its basis set.[1][9] Sinc functions have the useful property of being orthonormal and complete, making them a robust choice for representing wavefunctions.[10] The sinc-DVR method is valued for its accuracy and efficiency in a variety of applications, including:

  • Calculating molecular vibrational states.

  • Simulating quantum trajectories.[1]

  • Modeling superconducting circuits.[10]

  • Electronic structure calculations.[11][12]

Variants and Alternatives to sinc-DVR

While sinc-DVR is a powerful tool, other DVR methods and alternative numerical techniques exist, each with its own strengths and applications. The choice of method often depends on the specific problem and the boundary conditions of the system being studied.[12]

Method/VariantDescriptionKey Features
Traditional sinc-DVR Utilizes a basis of sinc functions, which are projections of a continuous Fourier basis.[10]High accuracy for problems with appropriate boundary conditions. The basis functions are localized around grid points.[13]
Truncated sinc-DVR A variation where the basis is finite and periodic over a defined interval.[10]Useful for systems with periodic boundary conditions. Can be more efficient for certain problems by limiting the basis size.[10]
Gauss-Hermite DVR Based on Hermite polynomials, suitable for problems with harmonic oscillator-like potentials.[12]Well-suited for systems where the wavefunction is localized and approaches zero at the boundaries.
Sine DVR Employs sine functions as the basis, often used for particle-in-a-box type problems.[12]Appropriate for systems with fixed zero-value boundary conditions.
Finite Difference Method An alternative numerical method that approximates derivatives on a grid.Conceptually simpler than DVR but often requires a finer grid to achieve comparable accuracy.
Finite Element Method A technique that represents the wavefunction locally with low-order polynomials.[2]Highly successful for partial differential equations in 2D and 3D but has seen less success in quantum problems.[2]

Experimental Protocols and Data Presentation

As "this compound" does not correspond to a known scientific instrument or method in the context of sinc-DVR, there are no experimental protocols or quantitative data to present for a direct comparison. The performance of different DVR methods is typically evaluated through numerical experiments on well-defined quantum mechanical problems. The key metrics for comparison in such studies are accuracy (e.g., convergence of energy eigenvalues) and computational efficiency (e.g., CPU time and memory requirements).

Logical Workflow for Selecting a DVR Method

The process of choosing an appropriate DVR method for a given research problem can be visualized as a logical workflow. This decision is guided by the physical characteristics of the system under investigation.

DVR_Selection_Workflow start Define Quantum System and Problem boundary_conditions Analyze Boundary Conditions start->boundary_conditions potential_shape Characterize Potential Energy Surface start->potential_shape periodic Periodic? boundary_conditions->periodic Yes zero_boundary Zero at Boundaries? boundary_conditions->zero_boundary No harmonic Harmonic-like? potential_shape->harmonic Yes general_potential General/Complex Potential potential_shape->general_potential No fourier_dvr Use Fourier or Truncated sinc-DVR periodic->fourier_dvr unbounded Unbounded? zero_boundary->unbounded No sine_dvr Use Sine DVR zero_boundary->sine_dvr Yes sinc_ho_dvr Use sinc-DVR or Gauss-Hermite DVR unbounded->sinc_ho_dvr ho_dvr Gauss-Hermite DVR is a strong candidate harmonic->ho_dvr general_dvr sinc-DVR is a versatile choice general_potential->general_dvr

Workflow for selecting a suitable DVR method.

References

A Comparative Guide to DVR-01 for Calculating Reaction Probabilities

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

This guide provides an objective comparison of the Discrete Variable Representation (DVR) method, here referred to as DVR-01, for calculating reaction probabilities against other established computational techniques. The information presented is supported by experimental and computational data to assist researchers in selecting the most appropriate method for their specific needs.

Introduction to this compound

The Discrete Variable Representation (DVR) is a powerful grid-based method used in quantum mechanics to solve the Schrödinger equation for molecular systems. In the context of chemical reaction dynamics, DVR provides a robust framework for calculating state-to-state and cumulative reaction probabilities. The "this compound" designation in this guide refers to the foundational DVR method, often employed with Absorbing Boundary Conditions (ABC), which has been instrumental in advancing the field of theoretical and computational chemistry. This approach offers a balance of accuracy and computational efficiency, making it a valuable tool for studying the dynamics of chemical reactions.

Comparison of Computational Methods for Reaction Probability Calculation

The choice of computational method for calculating reaction probabilities depends on a trade-off between accuracy, computational cost, and the specific characteristics of the chemical system under investigation. Below is a comparison of DVR with several alternative methods.

MethodPrincipleAdvantagesDisadvantagesTypical Applications
Discrete Variable Representation (DVR) Grid-based representation of the wavefunction. The potential energy operator is diagonal in this representation.- Computationally efficient for systems with smooth potential energy surfaces. - Avoids the calculation of multi-dimensional integrals. - The Hamiltonian matrix is often sparse, allowing for efficient diagonalization.- The size of the grid can become very large for high-dimensional systems. - Can be less efficient for systems with highly structured potential energy surfaces.- Gas-phase triatomic and small polyatomic reactions. - Photodissociation dynamics. - Calculation of vibrational energy levels.
S-matrix Kohn Variational Method A variational method for calculating the scattering matrix (S-matrix), from which reaction probabilities are derived.- Can be very accurate and efficient, especially when combined with a good basis set. - Often requires a smaller basis set than grid-based methods for comparable accuracy.- The resulting linear equations can be ill-conditioned. - Implementation can be more complex than DVR.- Benchmark calculations for small chemical reactions. - Electron-molecule scattering.
Finite Basis Representation (FBR) The wavefunction is expanded in a set of known basis functions (e.g., Gaussian or sine functions).- Well-established and widely used. - Can be very accurate if a suitable basis set is chosen.- Requires the calculation of multi-dimensional integrals of the potential energy, which can be computationally expensive. - The choice of basis set can significantly impact the accuracy and efficiency.- Electronic structure calculations. - Bound state calculations.
Time-Dependent Wave Packet Propagation The time evolution of a wave packet is simulated on a grid or with a basis set.- Provides a complete picture of the reaction dynamics over time. - Can be used to calculate a wide range of dynamical properties, including reaction probabilities, cross sections, and rate constants.- Can be computationally intensive, especially for long-time simulations or high-dimensional systems.- Reactions on surfaces. - Ultrafast chemical processes.
Quasi-Classical Trajectory (QCT) Classical trajectories of the atoms are simulated on the potential energy surface.- Computationally much less expensive than quantum methods. - Can be applied to larger and more complex systems.- Does not account for quantum effects such as tunneling and zero-point energy. - Can be inaccurate for reactions where quantum effects are important.- Reactions involving heavy atoms at high energies. - Initial screening of reaction dynamics.

Quantitative Performance Data

Direct quantitative comparison of computational cost and accuracy across a wide range of reactions is challenging due to the variability in implementation, system specifics, and desired precision. However, benchmark studies on well-characterized reactions provide valuable insights.

Case Study: The H + H₂ Reaction

The reaction H + H₂ → H₂ + H is a fundamental benchmark for quantum scattering methods. The following table summarizes a qualitative comparison based on published studies.

MethodRelative Computational Cost (for similar accuracy)Key Findings from Literature
DVR ModerateFor the collinear H + H₂ reaction, DVR-ABC has been shown to be a very efficient method for the direct calculation of the cumulative reaction probability, often requiring fewer grid points than needed for full state-to-state S-matrix calculations[1].
S-matrix Kohn Low to ModerateFor the collinear H + H₂ reaction, convergence in reaction probabilities was achieved with about 15% fewer basis functions compared to the number of DVR grid points required for similar accuracy[2][3].
Time-Dependent Wave Packet HighProvides accurate state-to-state and cumulative reaction probabilities and is a powerful tool for visualizing the reaction dynamics.

Experimental and Computational Protocols

Computational Protocol for DVR-ABC Calculation of Cumulative Reaction Probability

This protocol outlines the key steps for calculating the cumulative reaction probability N(E) for a bimolecular reaction using the DVR method with Absorbing Boundary Conditions (ABC).

  • Define the Coordinate System: Choose a suitable coordinate system to describe the reacting system. For an atom-diatom reaction like A + BC, Jacobi coordinates are commonly used.

  • Discretize the Hamiltonian: Represent the Hamiltonian operator on a multi-dimensional grid of points. In the DVR, the potential energy operator is a diagonal matrix where the diagonal elements are the potential energy values at each grid point. The kinetic energy operator has a known, structured representation.

  • Impose Absorbing Boundary Conditions (ABC): Introduce a negative imaginary potential at the edges of the grid. This "absorbing potential" prevents the artificial reflection of the wavefunction from the grid boundaries, mimicking the outgoing wave boundary conditions of a scattering experiment.

  • Calculate the Green's Function: The central quantity to compute is the Green's function, G(E) = (E - H)⁻¹, where H is the Hamiltonian including the absorbing potential. This is typically done by solving a system of linear equations.

  • Compute the Flux Operator: Define a dividing surface that separates reactants from products. The flux operator measures the flow of probability across this surface.

  • Calculate the Cumulative Reaction Probability: The cumulative reaction probability N(E) is then calculated from the trace of the Green's function and the flux operator.

Experimental Validation: Molecular Beam Experiments

Computational results for reaction probabilities are often validated against experimental data from crossed molecular beam experiments.

  • Prepare Reactant Beams: Two supersonic beams of the reactant molecules are generated with well-defined energies and internal quantum states.

  • Cross the Beams: The two beams are crossed at a specific angle in a high-vacuum chamber.

  • Detect Products: The scattered products are detected as a function of their angle and velocity, often using techniques like laser-induced fluorescence (LIF) or resonance-enhanced multiphoton ionization (REMPI) coupled with time-of-flight mass spectrometry.

  • Determine State-to-State Probabilities: By analyzing the angular and velocity distributions of the products in specific quantum states, the state-to-state differential cross-sections, and subsequently the reaction probabilities, can be determined.

Visualizations

Workflow for a DVR-based Reaction Probability Calculation

DVR_Workflow cluster_setup 1. System Setup cluster_dvr 2. DVR Calculation cluster_analysis 3. Analysis cluster_output 4. Output A Define Molecular System (e.g., A + BC) B Choose Coordinate System (e.g., Jacobi) A->B C Select Potential Energy Surface (PES) B->C D Construct DVR Grid C->D E Represent Hamiltonian in DVR D->E F Impose Absorbing Boundary Conditions (ABC) E->F G Calculate Green's Function F->G H Define Flux Dividing Surface G->H I Compute Flux Operator H->I J Calculate Reaction Probability N(E) I->J K Reaction Probabilities vs. Energy J->K L Rate Constants K->L

Caption: Workflow for calculating reaction probabilities using the DVR method.

Conceptual Comparison of Quantum Scattering Methods

Method_Comparison cluster_time_independent Time-Independent Methods cluster_time_dependent Time-Dependent Methods cluster_classical Classical/Semiclassical Methods DVR DVR (Grid-based) FBR FBR (Basis set) Kohn S-matrix Kohn (Variational) WavePacket Wave Packet Propagation QCT Quasi-Classical Trajectory Quantum Quantum Mechanical Methods Quantum->DVR Quantum->FBR Quantum->Kohn Quantum->WavePacket

Caption: Conceptual relationship between different methods for calculating reaction dynamics.

References

A Comparative Guide to Discrete Variable Representation (DVR) Methods in Computational Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals, the accurate and efficient calculation of molecular vibrational spectra is a critical task. The Discrete Variable Representation (DVR) method has emerged as a powerful and widely-used numerical technique for solving the nuclear Schrödinger equation to obtain vibrational energy levels and wavefunctions. This guide provides a comparative overview of common DVR methods, supported by available performance data, to aid in the selection of the most appropriate approach for a given research problem.

The core idea behind DVR is to transform the traditional basis set representation, known as the Finite Basis Representation (FBR), into a grid-based representation. In the DVR, the potential energy operator is represented by a diagonal matrix, where the diagonal elements are simply the values of the potential at specific grid points.[1] This feature significantly simplifies calculations, as the evaluation of complex integrals over basis functions is avoided.[2] The kinetic energy operator, while not diagonal, often has a simple, analytical form.[3] The relationship between FBR and DVR is a unitary transformation, meaning no information is lost in the conversion.[1]

Common DVR Methods: An Overview

Several DVR methods have been developed, each based on different underlying orthogonal polynomials or basis functions. The choice of the basis function implicitly defines the grid points and the accuracy of the representation. Key advantages of DVR methods include the sparsity of the resulting Hamiltonian matrix, which can be efficiently diagonalized, and the ability to prune the basis set by removing grid points in regions of high potential energy, thereby reducing computational cost, especially for polyatomic molecules.

Here, we compare some of the most frequently used DVR methods:

  • Harmonic Oscillator (HO) DVR: This method is based on the eigenfunctions of the harmonic oscillator, which are related to Hermite polynomials. It is a natural choice for systems where the potential is reasonably approximated by a harmonic potential, such as the vibrations of semi-rigid molecules. The grid points are the classical turning points of the harmonic oscillator.

  • Sine DVR: Based on a particle-in-a-box basis set (Fourier series), this DVR results in a grid of evenly spaced points.[4] It is particularly useful for systems with periodic or finite domains. The Colbert-Miller DVR is a well-known implementation of a DVR with a uniform grid.[4]

  • Potential Optimized DVR (PODVR): In this approach, the basis functions are the eigenstates of a one-dimensional reference Hamiltonian that includes the potential of interest.[5] This optimization of the basis set to the specific potential can lead to a significant reduction in the required number of grid points for a desired accuracy.[5]

  • Sinc DVR: This method, also pioneered by Colbert and Miller, provides an alternative derivation for a DVR on a uniform grid and offers analytic expressions for the kinetic energy operator.[1][3] It is closely related to the Sine DVR. Recent work has explored the use of Sinc DVRs for modeling superconducting circuits, highlighting their efficiency and convergence properties.[6]

  • Gauss Quadrature DVRs: This is a general class of DVRs where the grid points are the nodes of a Gaussian quadrature associated with a set of orthogonal polynomials (e.g., Legendre, Laguerre, Jacobi polynomials).[1] The choice of polynomial depends on the coordinate system and the nature of the problem. For example, DVRs based on Jacobi polynomials are suitable for angular coordinates.

Performance Comparison

Case Study: OH Stretching in Liquid Water

A study on the local OH stretching frequencies in liquid water compared a Harmonic Oscillator (HO) DVR with a uniform-grid DVR (Colbert-Miller type). To achieve high accuracy (errors of ~0.01%), the uniform-grid DVR required 41 grid points.[4] In contrast, the HO-DVR achieved a similar level of accuracy with a much smaller basis. For the HO-DVR, an optimal dimension of 10 basis functions (grid points) was found to predict the fundamental and first overtone transition energies with relative errors of less than 0.003% and 0.1%, respectively.[4] This demonstrates the efficiency gains possible by choosing a basis that is well-suited to the physical system.

MethodNumber of Grid PointsRelative Error (Fundamental)Relative Error (Overtone)Reference
Uniform-Grid DVR 41~0.01%~0.01%[4]
Harmonic Oscillator DVR 10<0.003%<0.1%[4]
Table 1. Comparison of the number of grid points and accuracy for Uniform-Grid DVR and Harmonic Oscillator DVR for the calculation of OH stretching frequencies in liquid water.
Case Study: Few-Body Quantum Systems

In a study of weakly bound triatomic systems like 7Li–He2, a DVR method based on an angular coordinate was shown to significantly reduce computation time compared to a classical algorithm using Legendre decomposition, without a loss of accuracy. While specific numbers are not presented in a table, convergence plots in the original study illustrate these gains.

Experimental and Computational Protocols

The general workflow for a DVR calculation involves several key steps. The specific implementation of each step will vary depending on the chosen DVR method and the molecular system under investigation.

1. Coordinate System and Hamiltonian: The first step is to define the internal coordinates of the molecule (e.g., bond lengths, angles) and derive the corresponding quantum mechanical Hamiltonian operator. This consists of a kinetic energy operator (KEO) and a potential energy surface (PES). The PES is typically obtained from high-level ab initio electronic structure calculations.

2. Choice of DVR Basis: A one-dimensional DVR basis is chosen for each degree of freedom. As discussed, common choices include Harmonic Oscillator functions, Sine functions, or functions based on other orthogonal polynomials. For multi-dimensional problems, a direct product of the one-dimensional bases is often used.

3. Construction of the Hamiltonian Matrix: The Hamiltonian operator is represented as a matrix in the DVR basis.

  • Potential Energy Matrix: In the DVR, this matrix is diagonal, with the diagonal elements being the values of the PES at the DVR grid points.

  • Kinetic Energy Matrix: The matrix elements of the KEO are typically calculated analytically in the chosen basis and then transformed to the DVR. For some DVRs, like the Sinc DVR, simple analytical formulas for the KEO matrix elements exist directly in the DVR.

4. Matrix Diagonalization: The resulting Hamiltonian matrix is diagonalized to obtain its eigenvalues and eigenvectors. The eigenvalues correspond to the vibrational energy levels of the molecule, and the eigenvectors are the coefficients of the vibrational wavefunctions in the DVR basis. Due to the sparsity of the DVR Hamiltonian, iterative diagonalization methods, such as the Lanczos algorithm, are often employed.

5. Basis Set Pruning (Optional but Recommended for larger systems): To reduce the computational cost, the direct-product DVR basis can be pruned. This involves removing grid points that correspond to very high potential energies, where the wavefunction is expected to have negligible amplitude. A common approach is to discard all basis functions associated with grid points where the potential energy is above a certain threshold.

Visualizing DVR Concepts

To better understand the relationships and workflows in DVR calculations, the following diagrams are provided.

DVR_Workflow cluster_setup 1. Setup cluster_construction 2. Hamiltonian Construction cluster_solve 3. Solve & Analyze A Define Molecular Coordinates & Obtain Potential Energy Surface (PES) B Choose 1D DVR Basis Sets (e.g., HO, Sine, PODVR) C Create Direct-Product DVR Grid B->C D Construct Diagonal Potential Energy Matrix V_DVR C->D E Construct Kinetic Energy Matrix T_DVR C->E F Assemble Hamiltonian H = T_DVR + V_DVR D->F E->F G Diagonalize Hamiltonian Matrix (e.g., Lanczos Algorithm) F->G H Obtain Eigenvalues (Energies) & Eigenvectors (Wavefunctions) G->H

A generalized workflow for DVR calculations.

DVR_Types cluster_quadrature Gauss Quadrature Based cluster_fourier Fourier Series Based cluster_optimized Optimized Basis DVR Discrete Variable Representation (DVR) HO_DVR Harmonic Oscillator DVR (Gauss-Hermite) DVR->HO_DVR Legendre_DVR Gauss-Legendre DVR DVR->Legendre_DVR Jacobi_DVR Gauss-Jacobi DVR DVR->Jacobi_DVR Sine_DVR Sine DVR DVR->Sine_DVR Sinc_DVR Sinc DVR (Colbert-Miller) DVR->Sinc_DVR PO_DVR Potential-Optimized DVR (PO-DVR) DVR->PO_DVR

Relationships between different types of DVR methods.

Conclusion

The Discrete Variable Representation offers a suite of powerful and efficient methods for the computational study of molecular vibrational spectroscopy. The choice of a specific DVR method depends on the nature of the molecular system and the coordinates used. For semi-rigid molecules with potentials that are well-approximated by a harmonic form, Harmonic Oscillator DVR can be highly efficient. For systems requiring a uniform grid or those with periodic boundary conditions, Sine or Sinc DVRs are excellent choices. For achieving high accuracy with a minimal basis size, especially for complex potential energy surfaces, Potential-Optimized DVR presents a compelling option. While a comprehensive, unified benchmark is still needed, the available evidence clearly indicates that a thoughtful selection of the DVR method can lead to significant gains in computational efficiency and accuracy, thereby accelerating research in chemistry, biology, and drug development.

References

A Head-to-Head Comparison: DVR-01 vs. Potential-Optimized DVR for the Quantum Dynamics of Floppy Molecules

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals navigating the complex landscape of computational molecular dynamics, the choice of numerical methods is paramount. This is especially true when studying "floppy" molecules—systems characterized by large-amplitude motions and weak intramolecular bonds, such as van der Waals complexes and certain biomolecules. In this guide, we provide an in-depth comparison of the standard Discrete Variable Representation (DVR) and the Potential-Optimized DVR (PO-DVR) methods, two powerful techniques for solving the Schrödinger equation for such challenging systems.

At the heart of computational quantum dynamics lies the need to represent the molecular wavefunction and operators in a way that is both accurate and computationally tractable. The Discrete Variable Representation (DVR) offers an elegant solution by transforming the basis representation of the wavefunction into a grid-point representation. In this framework, the potential energy operator becomes a simple diagonal matrix of potential values at each grid point, significantly simplifying calculations.

However, the efficiency of the standard DVR method, which we will refer to as DVR-01 for the purpose of this comparison, can be limited, particularly for floppy molecules where the wavefunction may be highly delocalized or concentrated in specific regions of the potential energy surface. This is where the Potential-Optimized DVR (PO-DVR) method offers a significant advantage. PO-DVR is a specialized form of DVR where the basis functions are not generic orthogonal polynomials but are instead optimized for the specific potential energy surface of the molecule under study. This tailored approach can lead to more compact basis sets, faster convergence, and ultimately, more efficient and accurate calculations.

Performance Comparison: this compound vs. PO-DVR

The primary advantage of PO-DVR over a standard DVR approach lies in its efficiency. By incorporating information about the potential energy into the basis set, PO-DVR can achieve the same level of accuracy with a significantly smaller basis. This is particularly crucial for multidimensional systems, where the size of the basis set grows exponentially with the number of degrees of freedom. For floppy molecules, where large-amplitude motion necessitates a wide range of basis functions, this optimization is especially beneficial.

While direct side-by-side benchmark data for a single floppy molecule is scarce in the literature, the principles of the methods and results from various studies consistently point to the superior performance of PO-DVR in terms of computational cost and efficiency.

FeatureStandard DVR (this compound)Potential-Optimized DVR (PO-DVR)
Basis Functions Based on general orthogonal polynomials (e.g., Legendre, Hermite) or a simple grid (e.g., sine functions).Derived from the eigenstates of a reference one-dimensional Hamiltonian that approximates the true potential.
Basis Set Size Often requires a larger basis set to achieve convergence, especially for complex potential energy surfaces.Typically requires a smaller, more compact basis set for the same level of accuracy.[1]
Computational Cost Can be computationally expensive for multidimensional systems due to the large basis set required.Generally more computationally efficient due to the smaller basis set, leading to faster calculations.[1]
Accuracy Can achieve high accuracy, but may require a very large basis set.Can achieve high accuracy with a more compact basis, leading to better convergence.
Applicability Widely applicable to a variety of quantum mechanical problems.Particularly well-suited for systems with complex potential energy surfaces and large-amplitude motion, such as floppy molecules.[2]

Experimental and Computational Protocols

The implementation of both this compound and PO-DVR methods involves a series of well-defined computational steps. The key difference lies in the initial step of defining the basis functions.

Standard DVR (this compound) Protocol

A common implementation of a standard DVR, such as a sine DVR, follows these general steps:

  • Define the Coordinate System: Choose a set of internal coordinates that appropriately describe the geometry of the floppy molecule.

  • Select a Primitive Basis Set: Choose a set of one-dimensional basis functions for each coordinate. For a simple DVR, this could be the eigenfunctions of a particle in a box (sine functions).

  • Establish the Grid: The DVR points are determined by the chosen basis set. For a sine DVR, the grid points are equally spaced.

  • Construct the Hamiltonian Matrix:

    • The potential energy operator (V) is represented as a diagonal matrix where the diagonal elements are the values of the potential energy at each DVR grid point, V_ii = V(q_i).

    • The kinetic energy operator (T) matrix elements are calculated in the chosen basis. For many standard bases, analytical expressions for these matrix elements are available.

  • Diagonalize the Hamiltonian: The resulting Hamiltonian matrix is diagonalized to obtain the eigenvalues (energy levels) and eigenvectors (wavefunctions).

Potential-Optimized DVR (PO-DVR) Protocol

The PO-DVR protocol introduces a crucial optimization step at the beginning:

  • Define the Coordinate System: As with the standard DVR, appropriate internal coordinates are chosen.

  • Define 1D Reference Hamiltonians: For each degree of freedom, a one-dimensional reference Hamiltonian is constructed. This is typically done by fixing the other coordinates at their equilibrium or another representative geometry and using the resulting 1D slice of the full potential energy surface.

  • Solve the 1D Schrödinger Equations: The 1D Schrödinger equations for these reference Hamiltonians are solved to obtain a set of eigenfunctions. These eigenfunctions form the potential-optimized basis.

  • Generate the PO-DVR Basis and Grid: The obtained eigenfunctions are used to generate the localized PO-DVR basis functions and the corresponding grid points.

  • Construct and Diagonalize the Full Hamiltonian: The full multidimensional Hamiltonian matrix is then constructed in this PO-DVR basis, and the potential energy operator is again represented as a diagonal matrix of potential values at the PO-DVR grid points. The matrix is then diagonalized to obtain the desired energy levels and wavefunctions.[1]

Logical Workflow Comparison

The following diagrams illustrate the key differences in the logical workflow between a standard DVR and a PO-DVR calculation.

DVR_Workflow cluster_dvr Standard DVR (this compound) Workflow dvr_start Define Coordinates & Standard Basis (e.g., Sine) dvr_grid Generate Uniform Grid dvr_start->dvr_grid dvr_hamiltonian Construct Hamiltonian Matrix (V is diagonal) dvr_grid->dvr_hamiltonian dvr_diag Diagonalize Hamiltonian dvr_hamiltonian->dvr_diag dvr_end Eigenvalues & Eigenvectors dvr_diag->dvr_end

Figure 1: Logical workflow for a standard DVR calculation.

PODVR_Workflow cluster_podvr Potential-Optimized DVR (PO-DVR) Workflow podvr_start Define Coordinates podvr_ref Define 1D Reference Hamiltonians podvr_start->podvr_ref podvr_solve Solve 1D Schrödinger Equations podvr_ref->podvr_solve podvr_basis Generate PO-DVR Basis & Grid podvr_solve->podvr_basis podvr_hamiltonian Construct Hamiltonian Matrix (V is diagonal) podvr_basis->podvr_hamiltonian podvr_diag Diagonalize Hamiltonian podvr_hamiltonian->podvr_diag podvr_end Eigenvalues & Eigenvectors podvr_diag->podvr_end

Figure 2: Logical workflow for a PO-DVR calculation.

Conclusion

For researchers engaged in the study of floppy molecules, the choice between a standard DVR and a PO-DVR method can have significant implications for the efficiency and feasibility of their calculations. While the standard DVR provides a robust and general framework, the PO-DVR method offers a more tailored and computationally efficient approach. By incorporating knowledge of the potential energy landscape into the basis set, PO-DVR can significantly reduce the size of the required basis, leading to faster and more manageable computations without sacrificing accuracy. This makes PO-DVR a particularly powerful tool for tackling the complex quantum dynamics of floppy molecules, ultimately enabling more precise predictions of their spectroscopic properties and behavior, a crucial aspect in fields ranging from fundamental chemical physics to drug design.

References

Safety Operating Guide

Important Notice: Substance Identification

Author: BenchChem Technical Support Team. Date: November 2025

Initial searches for "DVR-01" did not yield information on a chemical substance. The identifier "this compound" is commonly associated with electronic devices, specifically Digital Video Recorders. The following procedures are provided as a general template for the proper disposal of a hypothetical hazardous laboratory chemical, hereafter referred to as "Chemical-01."

Researchers, scientists, and drug development professionals must consult the specific Safety Data Sheet (SDS) and institutional safety guidelines for any chemical before handling and disposal. The information below is for illustrative purposes and should be adapted to the known properties and hazards of the actual substance being handled.

Essential Safety and Logistical Information for "Chemical-01" Disposal

This guide provides a procedural, step-by-step framework for the safe and compliant disposal of a hypothetical hazardous chemical, "Chemical-01." Adherence to these protocols is essential for ensuring personnel safety and environmental protection.

Data Presentation: "Chemical-01" Properties and Disposal Information

The following table summarizes hypothetical quantitative data relevant to the disposal of "Chemical-01." This data must be replaced with actual values from the substance-specific SDS.

PropertyValueSignificance for Disposal
pH 2.5 (1% solution)Corrosive (Acidic). Requires neutralization if sewer disposal is permitted; otherwise, must be collected as corrosive waste.
Flash Point 25°CFlammable. Must be stored away from ignition sources and collected as flammable waste.
Toxicity (LD50) 50 mg/kg (Oral, Rat)Acutely Toxic. Requires specific handling procedures and cannot be disposed of as regular trash.
Solubility in Water 5 g/LPartially soluble. Affects rinsing procedures and potential for sewer disposal.
Reactivity Reacts violently with oxidizing agentsIncompatible with certain chemical classes; requires segregated waste storage.
Regulatory Status EPA Hazardous Waste Code: D001, D002, P0XXDictates that the waste is regulated and must be managed through a licensed hazardous waste vendor.

Experimental Protocols: Detailed Disposal Methodology

The following protocol outlines the step-by-step procedure for the collection and disposal of "Chemical-01" waste. This process should be performed in a designated Satellite Accumulation Area (SAA).[1][2][3][4][5]

Personal Protective Equipment (PPE) and Preparation

1.1. Verify PPE: Before handling "Chemical-01," ensure appropriate PPE is worn, including but not limited to:

  • Chemical splash goggles
  • Appropriate chemical-resistant gloves (e.g., nitrile, neoprene)
  • Flame-resistant lab coat
  • Closed-toe shoes

1.2. Prepare Satellite Accumulation Area (SAA):

  • Ensure the SAA is at or near the point of waste generation.[1][4]
  • Verify that secondary containment is in place and free of contamination.[6][7]
  • Confirm that incompatible wastes are properly segregated.[3][8] For "Chemical-01," this means storing it separately from bases and oxidizing agents.

Waste Collection and Container Management

2.1. Select Appropriate Container:

  • Use a container made of a material compatible with acidic and flammable liquids (e.g., borosilicate glass or appropriate plastic).[3][7]
  • The container must be in good condition with no cracks or leaks and have a secure, screw-top cap.[1][7]

2.2. Label the Waste Container:

  • Before adding any waste, affix a "Hazardous Waste" label to the container.[6][7]
  • Fill in all required information on the label:
  • The words "Hazardous Waste".[6]
  • Full chemical name: "Chemical-01 Waste" and list all components of any mixture by percentage.[6][7]
  • Associated hazards (e.g., Flammable, Corrosive, Toxic).[6]
  • The date waste is first added to the container (accumulation start date).

2.3. Transferring Waste:

  • Perform all waste transfers inside a certified chemical fume hood.
  • Use a funnel to prevent spills. Do not leave the funnel in the container after use.[1]
  • Securely cap the container immediately after adding waste. Containers must remain closed at all times except when adding or removing waste.[1][6][9]

Management of Full Containers and Disposal Requests

3.1. Monitor Container Volume:

  • Do not fill the container beyond 90% capacity to allow for expansion.[3]
  • A maximum of 55 gallons of hazardous waste (or 1 quart of acutely hazardous waste) may be accumulated in an SAA.[1][2][10]

3.2. Procedure for Full Containers:

  • Once the container is full, complete the date on the hazardous waste label.
  • Submit a chemical waste collection request to your institution's Environmental Health & Safety (EHS) department.[9]

3.3. Disposal of Empty "Chemical-01" Containers:

  • Due to its acute toxicity, containers that held "Chemical-01" must be triple-rinsed with a suitable solvent.[7][9]
  • The rinsate (the liquid from rinsing) must be collected and disposed of as "Chemical-01" hazardous waste.[7][9]
  • After triple-rinsing, deface the original label and dispose of the container as regular trash or as directed by institutional policy.[9]

Mandatory Visualization: Disposal Workflow

The following diagram illustrates the logical workflow for the proper disposal of "Chemical-01."

G start Start: Waste Generation ppe 1. Don Correct PPE start->ppe prep_saa 2. Prepare Satellite Accumulation Area (SAA) ppe->prep_saa get_container 3. Select & Label Compatible Waste Container prep_saa->get_container transfer 4. Transfer Waste into Container in Fume Hood get_container->transfer is_full 5. Is Container Full? transfer->is_full cap_store 6. Securely Cap and Store in SAA is_full->cap_store No request_pickup 7. Request EHS Pickup is_full->request_pickup  Yes cap_store->transfer Add more waste later end_process End: Waste Removed by EHS request_pickup->end_process

Caption: Workflow for "Chemical-01" Hazardous Waste Disposal.

References

Personal protective equipment for handling DVR-01

Author: BenchChem Technical Support Team. Date: November 2025

Extensive searches for "DVR-01" have exclusively yielded results pertaining to Digital Video Recorders used in surveillance and electronic systems. There is no publicly available information to suggest that "this compound" is a designation for a chemical compound, laboratory reagent, or any substance that would require special personal protective equipment (PPE) for handling in a research, scientific, or drug development context.

The provided search results consistently refer to the physical installation, operation, and safety of electronic DVR devices, including warnings about electrical hazards and proper ventilation. The content does not contain any information relevant to chemical safety, handling protocols, disposal plans, or biological signaling pathways as requested.

To fulfill your request, please provide a more specific identifier for the substance of interest, such as:

  • A full chemical name

  • A Chemical Abstracts Service (CAS) number

  • The nature of the substance (e.g., small molecule, protein, nanoparticle)

Without additional information, it is not possible to provide the essential safety and logistical information, operational and disposal plans, or any of the other detailed requirements outlined in your request.

×

Retrosynthesis Analysis

AI-Powered Synthesis Planning: Our tool employs the Template_relevance Pistachio, Template_relevance Bkms_metabolic, Template_relevance Pistachio_ringbreaker, Template_relevance Reaxys, Template_relevance Reaxys_biocatalysis model, leveraging a vast database of chemical reactions to predict feasible synthetic routes.

One-Step Synthesis Focus: Specifically designed for one-step synthesis, it provides concise and direct routes for your target compounds, streamlining the synthesis process.

Accurate Predictions: Utilizing the extensive PISTACHIO, BKMS_METABOLIC, PISTACHIO_RINGBREAKER, REAXYS, REAXYS_BIOCATALYSIS database, our tool offers high-accuracy predictions, reflecting the latest in chemical research and data.

Strategy Settings

Precursor scoring Relevance Heuristic
Min. plausibility 0.01
Model Template_relevance
Template Set Pistachio/Bkms_metabolic/Pistachio_ringbreaker/Reaxys/Reaxys_biocatalysis
Top-N result to add to graph 6

Feasible Synthetic Routes

Reactant of Route 1
Reactant of Route 1
DVR-01
Reactant of Route 2
Reactant of Route 2
DVR-01

Featured Recommendations

Most viewed
Most popular with customers

Disclaimer and Information on In-Vitro Research Products

Please be aware that all articles and product information presented on BenchChem are intended solely for informational purposes. The products available for purchase on BenchChem are specifically designed for in-vitro studies, which are conducted outside of living organisms. In-vitro studies, derived from the Latin term "in glass," involve experiments performed in controlled laboratory settings using cells or tissues. It is important to note that these products are not categorized as medicines or drugs, and they have not received approval from the FDA for the prevention, treatment, or cure of any medical condition, ailment, or disease. We must emphasize that any form of bodily introduction of these products into humans or animals is strictly prohibited by law. It is essential to adhere to these guidelines to ensure compliance with legal and ethical standards in research and experimentation.

Quick Inquiry

Name *

Email *

Phone

Country

Product Name

Quantity *

Message