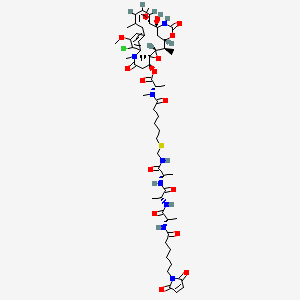
molecular formula C58H83ClN8O16S B13910615 DM21

DM21

Cat. No.: B13910615
M. Wt: 1215.8 g/mol
InChI Key: SJIJPSFCGJDQNG-ZPKZLEQESA-N
Attention: For research use only. Not for human or veterinary use.
Usually In Stock
  • Click on QUICK INQUIRY to receive a quote from our team of experts.
  • With the quality product at a COMPETITIVE price, you can focus more on your research.

Description

DM21 is a useful research compound. Its molecular formula is C58H83ClN8O16S and its molecular weight is 1215.8 g/mol. The purity is usually 95%.
BenchChem offers high-quality this compound suitable for many research applications. Different packaging options are available to accommodate customers' requirements. Please inquire for more information about this compound including the price, delivery time, and more detailed information at info@benchchem.com.

Properties

Molecular Formula

 C58H83ClN8O16S

Molecular Weight

 1215.8 g/mol

IUPAC Name

 [(1S,2R,3S,5S,6S,16Z,18Z,20R,21S)-11-chloro-21-hydroxy-12,20-dimethoxy-2,5,9,16-tetramethyl-8,23-dioxo-4,24-dioxa-9,22-diazatetracyclo[19.3.1.110,14.03,5]hexacosa-10,12,14(26),16,18-pentaen-6-yl] (2S)-2-[6-[[[(2S)-2-[[(2R)-2-[[(2S)-2-[6-(2,5-dioxopyrrol-1-yl)hexanoylamino]propanoyl]amino]propanoyl]amino]propanoyl]amino]methylsulfanyl]hexanoyl-methylamino]propanoate

InChI

 InChI=1S/C58H83ClN8O16S/c1-33-19-18-20-43(80-11)58(78)31-42(81-56(77)64-58)34(2)51-57(7,83-51)44(30-49(72)66(9)40-28-39(27-33)29-41(79-10)50(40)59)82-55(76)38(6)65(8)46(69)22-15-13-17-26-84-32-60-52(73)35(3)62-54(75)37(5)63-53(74)36(4)61-45(68)21-14-12-16-25-67-47(70)23-24-48(67)71/h18-20,23-24,28-29,34-38,42-44,51,78H,12-17,21-22,25-27,30-32H2,1-11H3,(H,60,73)(H,61,68)(H,62,75)(H,63,74)(H,64,77)/b20-18-,33-19-/t34-,35+,36+,37-,38+,42+,43-,44+,51+,57+,58+/m1/s1

InChI Key

 SJIJPSFCGJDQNG-ZPKZLEQESA-N

Isomeric SMILES

 C[C@@H]1[C@@H]2C[C@]([C@@H](/C=C\C=C(/CC3=CC(=C(C(=C3)OC)Cl)N(C(=O)C[C@@H]([C@]4([C@H]1O4)C)OC(=O)[C@H](C)N(C)C(=O)CCCCCSCNC(=O)[C@H](C)NC(=O)[C@@H](C)NC(=O)[C@H](C)NC(=O)CCCCCN5C(=O)C=CC5=O)C)\C)OC)(NC(=O)O2)O

Canonical SMILES

 CC1C2CC(C(C=CC=C(CC3=CC(=C(C(=C3)OC)Cl)N(C(=O)CC(C4(C1O4)C)OC(=O)C(C)N(C)C(=O)CCCCCSCNC(=O)C(C)NC(=O)C(C)NC(=O)C(C)NC(=O)CCCCCN5C(=O)C=CC5=O)C)C)OC)(NC(=O)O2)O

Origin of Product

 United States

Foundational & Exploratory

What is the DeepMind DM21 functional?

Author: BenchChem Technical Support Team. Date: November 2025

An In-Depth Technical Guide to the DeepMind DM21 Functional

For Researchers, Scientists, and Drug Development Professionals

Introduction

In the realm of computational chemistry and materials science, Density Functional Theory (DFT) stands as a cornerstone for predicting the electronic structure and properties of molecules and materials. The accuracy of DFT calculations hinges on the exchange-correlation (XC) functional, an approximation of the complex many-body electron interactions. For decades, the development of increasingly accurate XC functionals has been a central challenge. Traditional functionals, while successful in many areas, suffer from systematic errors, notably the delocalization error and the spin symmetry breaking error, which can lead to qualitatively incorrect predictions for systems with fractional charges or spins.

In 2021, researchers at DeepMind introduced this compound, a machine-learned density functional designed to overcome these fundamental limitations.[1][2][3] By training a neural network on both accurate chemical data and fractional electron constraints, this compound represents a significant step towards a more universally accurate and reliable DFT.[1][2][3] This technical guide provides a comprehensive overview of the this compound functional, its underlying methodology, performance, and practical applications.

Core Concepts of the this compound Functional

The this compound functional is a machine-learned, local hybrid functional that addresses key shortcomings of traditional DFT approximations.[4] Unlike conventional functionals that are based on analytical mathematical forms, this compound employs a neural network to learn the mapping from electron density to the exchange-correlation energy.[4][5][6]

Overcoming Delocalization and Spin Symmetry Errors

A key innovation of this compound is its explicit training on systems with fractional charges and fractional spins.[3][7] This training strategy directly tackles two persistent problems in DFT:

  • Delocalization Error: Many standard functionals tend to artificially spread out the electron density over multiple atoms or molecules, leading to incorrect descriptions of charge transfer and reaction barriers.[7][8] this compound, by being trained to recognize the correct piecewise linear behavior of the energy as a function of electron number, significantly reduces this error.[7][9] For example, in a system of two well-separated molecules, traditional functionals might incorrectly predict a partial charge on both, whereas this compound correctly localizes the charge on one of the molecules.[8]

  • Spin Symmetry Breaking: In the description of bond breaking and diradicals, many functionals incorrectly favor solutions with broken spin symmetry, leading to inaccurate potential energy surfaces. This compound is trained to preserve spin symmetry where appropriate, resulting in a more physical description of these challenging systems.[1][7]

Architecture and Inputs

The core of the this compound functional is a multilayer perceptron (MLP) neural network.[4][5] This network takes as input a set of local descriptors of the electron density at each point in space. These descriptors, or features, are sampled on a spatial grid and include:

  • The electron density itself.

  • The gradient of the electron density.

  • The kinetic energy density.

  • Local Hartree-Fock exchange energy features.[10]

The neural network then outputs the exchange-correlation energy density, which is integrated to give the total exchange-correlation energy.

Performance and Benchmarking

This compound has been rigorously tested on a variety of standard quantum chemistry benchmarks, demonstrating significant improvements over many widely used functionals.

Quantitative Performance Data

The following tables summarize the performance of this compound in comparison to other well-established density functionals on several key benchmarks. Errors are reported as Mean Absolute Error (MAE) in kcal/mol.

Table 1: Performance on the GMTKN55 Benchmark [4][10]

The General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions 55 (GMTKN55) benchmark is a comprehensive test suite for chemical accuracy.

FunctionalOverall MAE (kcal/mol)
This compound 1.5
SCAN3.6
B3LYP4.4
PBE8.7

Table 2: Performance on the Bond-Breaking Benchmark (BBB) [4][7]

The BBB benchmark assesses the ability of functionals to correctly describe the dissociation of molecules.

FunctionalMAE for Cation Dimers (kcal/mol)MAE for Neutral Dimers (kcal/mol)
This compound 1.2 1.8
SCAN7.34.5
B3LYP6.25.1
PBE9.87.2

Table 3: Performance on the QM9 Benchmark [4]

The QM9 dataset contains geometric, energetic, electronic, and thermodynamic properties for 134,000 small organic molecules.

FunctionalMAE for Atomization Energies (kcal/mol)
This compound 2.4
B97-D34.1
PBE7.8
Limitations in Transition Metal Chemistry

While this compound shows excellent performance for main-group chemistry, its application to transition metal chemistry (TMC) has revealed some limitations. Studies have shown that this compound can struggle with self-consistent field (SCF) convergence for many transition metal complexes. Although the accuracy, when converged, is often comparable or even superior to functionals like B3LYP, the convergence difficulties can make it impractical for routine use in this domain. However, using this compound to evaluate the energy non-self-consistently on top of a converged density from a different functional (e.g., B3LYP) has shown promise for improving accuracy in TMC.

Methodologies and Experimental Protocols

The evaluation and application of the this compound functional rely on standard computational chemistry workflows.

Software and Implementation

The this compound functional is publicly available as an extension to the open-source quantum chemistry software package, PySCF.[4][5] This allows researchers to readily incorporate this compound into their existing computational workflows.

Computational Details for Benchmarking

The performance data presented in Section 3 was generated using the following typical computational protocol:

  • Software: PySCF

  • Basis Set: A high-quality basis set, such as def2-QZVP, is typically used to ensure that the results are not limited by the basis set size.

  • Self-Consistent Field (SCF) Procedure: The SCF procedure is iterated until a tight convergence criterion is met. For this compound calculations, a convergence threshold of 10⁻⁶ Ha for the energy and 10⁻³ Ha/Bohr for the gradient is often used. Due to potential convergence issues, especially with transition metals, a robust SCF protocol may be necessary, potentially starting with a pre-converged density from a more stable functional.

  • Reference Data: The errors of the functionals are calculated with respect to high-accuracy reference data, typically from coupled-cluster with single, double, and perturbative triple excitations (CCSD(T)) or Quantum Monte Carlo (QMC) calculations.

Visualizing Key Workflows

To better understand the inner workings and application of the this compound functional, the following diagrams, generated using the DOT language, illustrate key processes.

The this compound Training Workflow

The training of the this compound neural network is a crucial step in its development. The following diagram outlines the major components of this process.

DM21_Training_Workflow cluster_data Training Data Generation cluster_training Neural Network Training cluster_output Output chemical_data Accurate Chemical Data (e.g., reaction energies) nn_model This compound Neural Network (Multilayer Perceptron) chemical_data->nn_model Input frac_charge_data Fractional Charge Data (e.g., atoms with non-integer electrons) frac_charge_data->nn_model Input frac_spin_data Fractional Spin Data (e.g., stretched H2) frac_spin_data->nn_model Input loss_function Loss Function (Regression + Gradient Regularization) nn_model->loss_function Prediction trained_functional Trained this compound Functional nn_model->trained_functional optimizer Optimizer (e.g., Adam) loss_function->optimizer optimizer->nn_model Update Weights

Caption: A schematic of the training workflow for the this compound neural network functional.

The Self-Consistent Field (SCF) Cycle with this compound

The SCF procedure is the iterative process used in DFT to find the ground-state electron density and energy. The following diagram illustrates how the this compound functional is incorporated into this cycle.

SCF_Cycle_with_this compound start Initial Guess Density (ρ₀) construct_ks Construct Kohn-Sham Matrix start->construct_ks solve_ks Solve Kohn-Sham Equations construct_ks->solve_ks dm21_functional Evaluate XC Potential with this compound Neural Network construct_ks->dm21_functional output_orbitals Obtain Orbitals (ψᵢ) solve_ks->output_orbitals calculate_density Calculate New Density (ρ_new) output_orbitals->calculate_density mix_density Mix Densities (ρ_in = f(ρ_new, ρ_old)) calculate_density->mix_density dm21_functional->construct_ks mix_density->construct_ks Next Iteration check_convergence Check for Convergence mix_density->check_convergence check_convergence->construct_ks No end Converged Energy and Density check_convergence->end Yes

References

The DM21 Functional: A Deep Dive into Machine Learning-Enhanced Density Functional Theory

Author: BenchChem Technical Support Team. Date: November 2025

A Technical Whitepaper for Researchers, Scientists, and Drug Development Professionals

Executive Summary

Density Functional Theory (DFT) is a cornerstone of modern computational chemistry and materials science, offering a balance of accuracy and computational cost. However, traditional DFT approximations have long been plagued by inherent limitations, such as delocalization error, which can lead to inaccurate predictions for a variety of chemical systems. The DeepMind 21 (DM21) functional represents a significant leap forward, leveraging deep learning to address these fundamental challenges.[1][2][3][4] This whitepaper provides an in-depth technical guide to the this compound functional, detailing its theoretical underpinnings, performance benchmarks, and practical applications, with a particular focus on its relevance to drug development.

Introduction to the this compound Functional

The this compound functional is a machine-learned exchange-correlation (XC) functional developed by DeepMind.[5] Unlike traditional functionals that are based on analytical expressions derived from physical approximations, this compound employs a neural network to learn the complex relationship between electron density and the exchange-correlation energy.[5][6] A key innovation of this compound is its explicit training to be free of delocalization error, a systematic failure of many popular functionals that leads to an overestimation of the stability of delocalized electronic states.[1][2][3][4] This is achieved by training the functional on systems with fractional charges and fractional spins, which, while not physically real, provide strong constraints on the exact functional.[1][5][7]

The architecture of this compound is a multilayer perceptron (MLP) that takes Kohn-Sham orbital features on a spatial grid as input to predict the exchange-correlation energy density.[5] This approach allows the functional to learn subtle and complex features of the electron density that are missed by traditional, human-designed functionals.

Core Concepts: Functional- vs. Density-Driven Errors

The accuracy of any DFT calculation is determined by the interplay of two types of errors: functional-driven and density-driven errors.[1][2][3][4]

  • Functional-Driven Error: This error arises from the inexactness of the approximate exchange-correlation functional itself. Even if the exact electron density were known, an approximate functional would still yield an approximate energy.

  • Density-Driven Error: This error results from the fact that an approximate functional will produce an approximate, and therefore incorrect, electron density. This incorrect density then leads to further errors in the calculated energy and other properties.

A significant advantage of this compound is that it is designed to be virtually free of density-driven error.[1] By accurately reproducing the piecewise-linear behavior of the exact Kohn-Sham functional for systems with fractional charges, this compound yields highly accurate electron densities.[1] This means that any remaining errors in this compound calculations are primarily functional-driven.[1]

Logical Relationship of Errors in DFT TotalError Total DFT Error FunctionalError Functional-Driven Error (Inaccuracy of the XC functional) TotalError->FunctionalError DensityError Density-Driven Error (Inaccuracy of the electron density) TotalError->DensityError ApproxFunctional Approximate XC Functional ApproxFunctional->FunctionalError directly causes ElectronDensity Self-Consistent Electron Density ApproxFunctional->ElectronDensity determines ElectronDensity->DensityError can be inaccurate, causing

Caption: Logical relationship between total DFT error and its components.

Performance Benchmarks

This compound has been rigorously tested on a variety of benchmark datasets, consistently demonstrating state-of-the-art performance that surpasses many widely used hybrid functionals and approaches the accuracy of much more computationally expensive double-hybrid functionals.[5][8]

General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55)

The GMTKN55 benchmark is a comprehensive test suite for main group thermochemistry, kinetics, and noncovalent interactions. This compound shows a significant improvement over traditional functionals on this benchmark.

FunctionalMean Absolute Error (kcal/mol) on GMTKN55
This compound 1.5 [9]
SCAN3.6[9]
Other Hybrids> 5[8]
Other Benchmarks

This compound also performs exceptionally well on other challenging benchmarks:

BenchmarkMetricThis compound PerformanceComparison
BBB (Bond-breaking Benchmark) Mean Absolute Error (kcal/mol)< 5[8]Outperforms the three best-performing hybrid functionals.[8]
QM9 Mean Absolute Error vs. G4(MP2)State-of-the-art[5][8]Outperforms four other previous methods.[5]
LMGB35 (Bond Lengths) Mean Absolute Error (pm)0.843 (6-31G(d,p)), 0.625 (def2-TZVP)[9]Comparable to PBE0 (0.803, 0.615) and SCAN (0.795, 0.608).[9]

Experimental and Computational Protocols

The evaluation and application of the this compound functional involve specific computational methodologies.

Geometry Optimization

A key consideration when using this compound is that analytical gradients for the neural network-based functional are not available.[9][10] Therefore, geometry optimizations must be performed using numerical gradients.

  • Method: Central finite difference methods are typically employed to calculate the nuclear gradients.[10]

  • Implementation: This requires multiple self-consistent field (SCF) calculations for each optimization step.[10]

  • Software: The this compound functional has been implemented in the PySCF (Python for Strongly Correlated Electron Systems) framework.[10]

  • Numerical Differentiation Step: A numerical differentiation step in the range of 0.0001–0.001 Å is recommended to obtain sufficiently smooth nuclear gradients.[6]

This compound Geometry Optimization Workflow start Initial Molecular Geometry scf Perform SCF Calculation with this compound Functional start->scf num_grad Calculate Numerical Gradients (Central Finite Difference) scf->num_grad update_geom Update Atomic Positions num_grad->update_geom check_conv Check for Convergence update_geom->check_conv check_conv->scf No end Optimized Geometry check_conv->end Yes

Caption: Workflow for geometry optimization using the this compound functional.

Benchmarking Protocols

The performance of this compound is typically assessed against high-level theoretical methods.

  • Reference Data: For benchmarks like BBB and GMTKN55, reference values are often obtained from highly accurate methods such as Coupled Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)) or Quantum Monte Carlo (QMC).[8] For the QM9 dataset, G4(MP2) theory is used as a reference.[8]

  • Basis Sets: The choice of basis set can influence the results. Studies have used basis sets such as 6-31G(d,p) and def2-TZVP.[9]

Applications in Drug Development

The high accuracy of the this compound functional, particularly in describing noncovalent interactions and reaction energetics, makes it a promising tool for various stages of the drug development pipeline.

  • Target Identification and Validation: Accurate modeling of protein-ligand interactions is crucial. This compound's ability to handle noncovalent interactions can lead to more reliable binding affinity predictions.

  • Lead Optimization: The accurate prediction of reaction barriers and thermochemistry can aid in the design of synthetic routes for novel drug candidates.

  • ADMET Prediction: While not directly demonstrated in the provided literature, the improved description of molecular properties could contribute to more accurate predictions of absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties.

Limitations and Future Directions

Despite its successes, this compound has some limitations.

  • Computational Cost: The numerical calculation of gradients makes geometry optimizations with this compound significantly slower than with analytical functionals.[6]

  • Extrapolation: The performance of this compound can be less reliable for systems that are very different from its training data. For instance, it has been shown to struggle with achieving self-consistent field (SCF) convergence for some transition metal chemistry (TMC) molecules, a class of systems not included in its training set.[7][11]

  • Condensed Phase Simulations: While promising, the application of this compound to condensed-phase systems, such as liquid water, has revealed challenges. The functional can overestimate hydrogen-bond strength, leading to a more "ice-like" local structure in simulations of liquid water at room temperature.[2][3][4]

Future work will likely focus on expanding the training datasets to include a wider range of chemical systems, developing more efficient methods for calculating gradients, and improving its performance for condensed-phase simulations.

Conclusion

The this compound functional represents a paradigm shift in the development of exchange-correlation functionals for DFT. By leveraging the power of machine learning, it overcomes some of the most persistent limitations of traditional methods. While challenges remain, particularly in terms of computational efficiency and a broader applicability to all areas of chemistry, this compound's impressive accuracy for a wide range of molecular systems makes it a valuable tool for researchers in drug development and beyond. Its development paves the way for a new generation of highly accurate and reliable DFT methods.

References

The Advent of Self-Learning Functionals: A Technical Guide to Machine-Learned Density Functional Theory

Author: BenchChem Technical Support Team. Date: November 2025

For Immediate Release

A new breed of Density Functional Theory (DFT) functionals, powered by machine learning (ML), is poised to revolutionize computational chemistry and drug discovery. These "self-learning" functionals promise to overcome some of the most significant accuracy and efficiency limitations of traditional DFT methods, offering a powerful new tool for researchers, scientists, and drug development professionals.

This in-depth technical guide provides a comprehensive overview of the core concepts, development methodologies, and applications of machine-learned DFT functionals. It is designed to equip researchers with the knowledge necessary to understand, evaluate, and potentially implement these cutting-edge computational tools in their own work.

Introduction: The Challenge of the Exchange-Correlation Functional

Density Functional Theory is a cornerstone of modern computational science, enabling the prediction of molecular and material properties from first principles.[1][2] At the heart of DFT lies the exchange-correlation (XC) functional, an elusive component that accounts for the complex quantum mechanical interactions between electrons.[3][4] For decades, the development of increasingly accurate XC functionals has been a central challenge in the field, following a "Jacob's Ladder" of approximations, with each rung offering improved accuracy at a higher computational cost.[5]

Machine learning offers a paradigm shift in this development process. Instead of relying on human intuition and complex mathematical derivations, ML algorithms can learn the intricate relationship between electron density and the exchange-correlation energy directly from high-quality reference data.[6][7] This data-driven approach has the potential to create functionals that are not only more accurate but also computationally efficient.[8][9]

The Core of Machine-Learned DFT: From Data to Functionals

The development of a machine-learned DFT functional is a multi-stage process that combines principles of quantum mechanics, computer science, and data science. The general workflow involves data generation, feature engineering, model training, and validation.

Data Generation: The Foundation of Accuracy

The performance of any machine-learning model is fundamentally limited by the quality and diversity of the data it is trained on. For ML-DFT functionals, this training data typically consists of:

  • Molecular Geometries: A diverse set of molecular structures.

  • Electron Densities: The corresponding electron density for each geometry.

  • High-Accuracy Energies and Forces: Calculated using highly accurate but computationally expensive methods like Coupled Cluster (CC) theory or Quantum Monte Carlo (QMC).[10]

Popular benchmark datasets used for training and evaluating ML-DFT functionals include QM9 and GMTKN55 .[11][12][13] The QM9 dataset contains information on over 130,000 small organic molecules, while GMTKN55 is a comprehensive benchmark suite for general main-group thermochemistry, kinetics, and noncovalent interactions.[12][13]

Data Preprocessing and Feature Engineering: Translating Chemistry for Machines

Raw data from quantum chemical calculations must be transformed into a format that is understandable by machine learning algorithms.[14][15][16][17][18] This crucial step, known as feature engineering, involves selecting and creating informative descriptors of the molecular system. Common features include:

  • Local Electron Density and its Derivatives: Capturing the immediate electronic environment.

  • Kinetic Energy Density: Providing information about the local electronic motion.

  • Atom-Centered Descriptors: Representing the chemical environment around each atom.

These features are then often scaled or normalized to improve the training process.[18]

DataPreprocessing RawData Raw Quantum Chemical Data (Geometries, Densities, Energies) FeatureEngineering Feature Engineering (Density Descriptors, etc.) RawData->FeatureEngineering  Extraction DataSplitting Data Splitting (Training, Validation, Test Sets) FeatureEngineering->DataSplitting  Transformation PreprocessedData Preprocessed Data for ML DataSplitting->PreprocessedData  Partitioning

A simplified workflow for data preprocessing in ML-DFT.
Model Architectures: Learning the Functional Form

Various machine learning architectures are employed to learn the mapping from the engineered features to the exchange-correlation energy. The most common are:

  • Neural Networks (NNs): Deep neural networks with multiple hidden layers can learn highly complex and non-linear relationships.[3][6]

  • Graph Neural Networks (GNNs): These are particularly well-suited for molecular data as they can directly operate on the graph structure of molecules, capturing atomic connectivity and relationships.[19][20][21]

The choice of architecture and its hyperparameters (e.g., number of layers, number of neurons per layer, activation functions) is a critical aspect of model development.[22]

Training and Validation: Optimizing for Predictive Power

The training process involves minimizing a loss function that quantifies the difference between the ML model's predictions and the high-accuracy reference data. This is typically done using gradient-based optimization algorithms. The model's performance is then evaluated on a separate validation set to prevent overfitting and ensure its ability to generalize to unseen data.

ModelTrainingWorkflow cluster_data Data Preparation cluster_model Model Development cluster_output Output TrainingData Training Data Training Training Loop (Minimize Loss Function) TrainingData->Training ValidationData Validation Data Evaluation Evaluation ValidationData->Evaluation Model Machine Learning Model (e.g., Neural Network) Model->Training Training->Evaluation Evaluation->Model Update Parameters TrainedFunctional Trained ML-DFT Functional Evaluation->TrainedFunctional Final Model ExperimentalProtocol Start Define Chemical Space & Target Properties DataGen Generate High-Fidelity Quantum Data Start->DataGen FeatureEng Feature Engineering & Preprocessing DataGen->FeatureEng ModelDesign Select & Design ML Model Architecture FeatureEng->ModelDesign Training Train Model on Training Data ModelDesign->Training Validation Validate & Tune on Validation Data Training->Validation Validation->Training Iterate Benchmarking Benchmark on Test Data & Standard Datasets Validation->Benchmarking Integration Integrate into QC Software Benchmarking->Integration End Deploy Functional for Applications Integration->End

References

DM21 Neural Network: A Technical Deep Dive into the Future of Quantum Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

For Immediate Release

A Technical Guide for Researchers, Scientists, and Drug Development Professionals

Google's DeepMind has introduced a groundbreaking neural network architecture, DM21, poised to revolutionize the field of quantum chemistry. This in-depth technical guide explores the core principles, experimental validation, and practical implementation of this compound, offering a comprehensive resource for professionals in drug development and scientific research. By providing a more accurate and efficient means of simulating molecular interactions at the quantum level, this compound opens new avenues for the design of novel therapeutics and materials.

Core Architecture and Functionality

The this compound is a sophisticated deep learning model designed to approximate the exchange-correlation functional within Density Functional Theory (DFT), a fundamental method in quantum chemistry for calculating the electronic structure of atoms and molecules.[1] Traditional DFT functionals often struggle with systems exhibiting "fractional electron character," leading to significant inaccuracies in predicting chemical properties.[1] this compound addresses this limitation through a novel neural network approach.

At its core, this compound is a multilayer perceptron (MLP) that takes a grid of electron densities as its input.[1] The architecture is designed to learn a mapping from these electron densities to the chemical interaction energy, a critical component in quantum mechanical modeling.[1]

A key innovation of this compound lies in its training methodology. The model was trained on a dataset of 1161 examples, which included not only data from real molecules but also from fictitious systems with fractional charges and spins.[2] This unique training strategy enables this compound to overcome the long-standing problems of delocalization and spin symmetry-breaking that have plagued previous DFT functionals.[2]

Experimental Protocols

The development and validation of the this compound neural network involved a meticulous set of experimental and computational protocols.

Training Dataset Composition

The training dataset for this compound was strategically assembled to address the shortcomings of traditional DFT functionals. It comprised 1161 data points, including:

  • Molecular Data: A diverse set of molecules to learn the fundamental relationships between electron density and energy.

  • Fractional Charge and Spin Systems: Fictitious atomic and molecular systems with non-integer numbers of electrons or spins. This data was crucial for teaching the model to handle electron delocalization and static correlation effects correctly. The training specifically included exact conditions for bare atoms with fractional charges and spins.[2]

Neural Network Training Procedure

The this compound MLP was trained using a supervised learning approach. The key components of the training protocol are outlined below:

  • Input Features: Kohn-Sham orbital features, including the spin-indexed charge density, the norm of its gradient, and the kinetic energy density, were sampled on an atom-centered quadrature grid.[2]

  • Loss Function: The training objective utilized a regression loss function to minimize the difference between the predicted and actual reaction energies. A crucial addition was a gradient regularization term . This term ensures that the learned functional is smooth and well-behaved, which is essential for its use in self-consistent field (SCF) calculations, a standard iterative procedure in quantum chemistry.[4]

Quantitative Performance Analysis

This compound has been rigorously benchmarked against a suite of established quantum chemistry methods and datasets. The results demonstrate a significant improvement in accuracy for a wide range of chemical systems.

Performance on Benchmark Datasets

This compound has shown state-of-the-art performance on several widely recognized benchmark datasets in quantum chemistry, including the Bond-breaking Benchmark (BBB), GMTKN55, and QM9.[1]

Benchmark DatasetThis compound Performance Metric (kcal/mol)Comparison with Traditional Functionals
GMTKN55 Mean Absolute Error: 1.5Outperforms SCAN (3.6 kcal/mol) and other classical functionals.[5]
BBB (selected diatomics) Lower Mean Absolute ErrorsSignificantly outperforms all tested classical DFT functionals.[6]
QM9 State-of-the-art performanceDemonstrates strong performance on a large and diverse set of organic molecules.

Table 1: Summary of this compound performance on key benchmark datasets. Errors are reported in kilocalories per mole (kcal/mol), a standard unit of energy in chemistry.

Comparison with Established Functionals

A detailed comparison of this compound with other widely used DFT functionals on the GMTKN55 benchmark reveals its superior performance across various classes of chemical reactions.

FunctionalMean of Means (MoM) Error (kcal/mol)
This compound ~2.5
revPBE:D3 BJ~4.0
SCAN:D3 BJ~3.5
PW6B95:D3 0~3.0
DSD-PBEP86:D3 BJ (Double Hybrid)~2.0

Table 2: Comparison of the Mean of Means (MoM) error metric for this compound and other functionals on the GMTKN55 benchmark.[7] this compound approaches the accuracy of the much more computationally expensive double-hybrid functionals.

Signaling Pathways and Workflow Diagrams

To provide a clearer understanding of the logical flow of information and computation within the this compound framework, the following diagrams have been generated using the DOT language.

This compound Training Workflow

The following diagram illustrates the key stages involved in training the this compound neural network.

DM21_Training_Workflow This compound Neural Network Training Workflow cluster_data Data Preparation cluster_training Model Training Molecular_Data Molecular Data Feature_Extraction Kohn-Sham Feature Extraction (Density, Gradient, Kinetic Energy) Molecular_Data->Feature_Extraction Fractional_Data Fractional Charge/Spin Data Fractional_Data->Feature_Extraction MLP Multilayer Perceptron (this compound) Feature_Extraction->MLP Input Features Loss_Function Loss Function (Regression + Gradient Regularization) MLP->Loss_Function Predicted Energy Optimizer Optimizer Loss_Function->Optimizer Gradients Optimizer->MLP Update Weights

A high-level overview of the this compound training process.
This compound Inference Workflow for a New Molecule

This diagram outlines the steps for using the trained this compound model to predict the energy of a new molecule.

DM21_Inference_Workflow This compound Inference Workflow New_Molecule New Molecular System SCF_Initial_Guess Initial Guess for Self-Consistent Field (SCF) New_Molecule->SCF_Initial_Guess SCF_Cycle SCF Cycle SCF_Initial_Guess->SCF_Cycle DM21_Functional Trained this compound Functional SCF_Cycle->DM21_Functional Electron Density Total_Energy Predicted Total Energy SCF_Cycle->Total_Energy Converged Solution DM21_Functional->SCF_Cycle Exchange-Correlation Potential

Workflow for predicting molecular energy using the trained this compound model.

Practical Implementation with PySCF

The this compound functional has been made publicly available and can be readily integrated into existing quantum chemistry workflows through the open-source PySCF software package.[1] This allows researchers to apply the power of this compound to their own systems of interest.

The implementation in PySCF allows for the replacement of traditional DFT functionals with the this compound neural network functional within the self-consistent field calculation. While a detailed tutorial is beyond the scope of this guide, the general procedure involves specifying the this compound functional in the input for a DFT calculation. Researchers have successfully implemented and tested this compound for various applications, including geometry optimization, within the PySCF framework.[5][8]

Conclusion and Future Outlook

The this compound neural network represents a significant leap forward in the field of quantum chemistry. By leveraging deep learning and a novel training strategy that incorporates fractional electron and spin constraints, this compound provides a more accurate and robust method for simulating molecular systems. Its demonstrated performance on a wide range of benchmarks and its availability in the PySCF package make it a powerful tool for researchers in drug discovery, materials science, and beyond. As research in this area continues, we can expect further refinements and applications of neural network-based functionals, paving the way for unprecedented accuracy and efficiency in computational chemistry.

References

The DM21 Functional: A Machine-Learned Approach to Overcoming Fundamental Challenges in DFT

Author: BenchChem Technical Support Team. Date: November 2025

A Technical Guide for Researchers, Scientists, and Drug Development Professionals

The DeepMind 21 (DM21) functional represents a significant advancement in the field of Density Functional Theory (DFT), leveraging machine learning to address long-standing systematic errors inherent in conventional functionals.[1][2] Developed by researchers at DeepMind, this compound employs a neural network to approximate the exchange-correlation functional, demonstrating state-of-the-art accuracy across a range of chemical benchmarks.[1][2] This technical guide provides an in-depth overview of the core advantages of the this compound functional, its performance metrics, and the computational methodologies for its application.

Core Advantages of the this compound Functional

The primary advantage of the this compound functional lies in its ability to mitigate the delocalization and spin symmetry-breaking errors that plague many widely used density functional approximations.[2] These errors stem from the incorrect description of systems with "fractional electron character," leading to significant inaccuracies in predicting reaction barriers, band gaps, and the properties of charged and open-shell species.

1. Mitigation of Fractional Charge and Spin Errors:

This compound was specifically trained to recognize and correctly handle systems with fractional charges and spins.[2][3] This allows for a more accurate description of:

  • Dissociation of covalent bonds: Traditional functionals often incorrectly predict that separated fragments retain a partial charge, a manifestation of the delocalization error. This compound provides a more physical description of bond breaking, leading to more accurate dissociation energy curves.[2]

  • Charged systems: The delocalization error can lead to an artificial spreading of charge in molecules, which is problematic for describing localized charges in, for example, amino acid side chains or drug-receptor interactions. This compound correctly localizes charge on a single molecule in a system of two adjacent molecules, unlike traditional functionals like B3LYP which may incorrectly smear the charge over both.[2]

  • Spin states: For systems with unpaired electrons, many functionals artificially break spin symmetry to achieve a lower energy state. This compound is designed to better preserve spin symmetry, providing a more accurate description of open-shell systems.[2]

2. High Accuracy on Benchmark Datasets:

This compound has demonstrated exceptional performance on a variety of established quantum chemistry benchmarks, often outperforming highly-parameterized hybrid and even approaching the accuracy of more computationally expensive double-hybrid functionals.[1]

3. Open-Source Availability:

The this compound functional is publicly available as an extension to the popular open-source quantum chemistry software package, PySCF, facilitating its adoption and use by the broader scientific community.[1]

Performance Benchmarks

The performance of this compound has been rigorously evaluated against a range of other DFT functionals on several key benchmark datasets. The following tables summarize the Mean Absolute Errors (MAEs) in kcal/mol for various chemical tasks.

Table 1: Performance on General Chemistry Benchmarks (kcal/mol)

FunctionalGMTKN55 (Overall MAE)QM9 (MAE)BBB (MAE)
This compound 1.5 [4]< 5 [5]Excellent Performance [6]
SCAN3.6[4]~5[5]-
ωB97X-V-~5[5]-
B3LYP-> 5[5]-
PBE-> 10[5]-

Table 2: Performance on Transition Metal Chemistry (TMC117 Dataset, kcal/mol)

MethodMedian Absolute ErrorMean Absolute Error (Converged)
This compound@this compound (self-consistent) 2.6 [7]3.13 [8]
This compound@B3LYP 2.3 [7]2.93 [8]
B3LYP@B3LYP (self-consistent)3.0[7]2.73[8]

Note: this compound can struggle with self-consistent field (SCF) convergence for some transition metal complexes.[7] Using the electron density from a converged B3LYP calculation (this compound@B3LYP) can be a practical approach to leverage the accuracy of this compound in these cases.[7]

Table 3: Performance for Water Clusters (Absolute Errors in kcal/mol relative to CCSD(T))

SystemThis compoundωB97M-VDC-SCAN
(H₂O)₂₋₁₀ Clusters (Interaction Energy)Varies with cluster size[9]Smaller MAE than this compound[9]Closest agreement with reference[9]
H₃O⁺(H₂O)ₙ & OH⁻(H₂O)ₙ (Binding Energy)Varies with cluster size[9]--
H₃O⁺(H₂O)ₙ & OH⁻(H₂O)ₙ (Interaction Energy)Varies with cluster size[9]--

Note: While this compound shows promise, its accuracy for the energetics of aqueous clusters can vary significantly with the size of the cluster.[9]

Computational Protocols

The following provides a general methodology for performing calculations using the this compound functional.

1. Software and Installation:

The this compound functional is implemented in the PySCF software library.[1] Installation instructions for PySCF and the this compound extension can be found on their respective GitHub repositories.

2. Single-Point Energy Calculations:

A typical script for a single-point energy calculation on a molecule using this compound in PySCF would involve:

  • Defining the molecule's geometry and basis set (e.g., def2-QZVPPD).

  • Specifying the 'this compound' functional.

  • Running the self-consistent field (SCF) calculation.

3. Geometry Optimization:

Geometry optimization with this compound requires numerical differentiation to compute the nuclear gradients, as analytical gradients are not yet available.[8] This can be computationally more demanding than with analytical gradient-enabled functionals. The optimization procedure involves:

  • Defining the molecule and basis set.

  • Specifying the 'this compound' functional.

  • Using a numerical gradient-based optimizer to find the minimum energy geometry.

4. Benchmark Evaluations:

To replicate the benchmark results, the following protocol is generally followed:

  • Obtain the molecular geometries for the desired benchmark set (e.g., GMTKN55, QM9).

  • For each molecule, perform a single-point energy calculation using this compound and the chosen basis set.

  • Calculate the relevant energy differences (e.g., reaction energies, atomization energies).

  • Compare the calculated values to the high-level theoretical reference values provided with the benchmark set to determine the error.

Visualizing the this compound Workflow and Logic

To better understand the conceptual underpinnings of this compound, the following diagrams illustrate its workflow and the problem it addresses.

DM21_Workflow This compound Computational Workflow cluster_input Input Features cluster_this compound This compound Neural Network cluster_output Output Electron_Density Electron Density (ρ) MLP Multilayer Perceptron (MLP) Electron_Density->MLP Density_Gradient Density Gradient (∇ρ) Density_Gradient->MLP Kinetic_Energy_Density Kinetic Energy Density (τ) Kinetic_Energy_Density->MLP Hartree_Fock_Exchange Local Hartree-Fock Exchange Hartree_Fock_Exchange->MLP XC_Energy Exchange-Correlation Energy (Exc) MLP->XC_Energy

Caption: Conceptual workflow of the this compound functional.

Fractional_Error_Logic Addressing Fractional Electron Errors with this compound cluster_problem The Problem in Conventional DFT cluster_solution The this compound Solution Fractional_Electrons Systems with Fractional Electron Character Delocalization_Error Delocalization Error (e.g., incorrect charge separation) Fractional_Electrons->Delocalization_Error Spin_Symmetry_Breaking Spin Symmetry Breaking (e.g., incorrect bond dissociation) Fractional_Electrons->Spin_Symmetry_Breaking Training_Data Training on Fractional Charge and Spin Data DM21_Functional This compound Neural Network Functional Training_Data->DM21_Functional Improved_Physics Correct Piecewise Linearity and Spin Symmetry DM21_Functional->Improved_Physics

Caption: Logical diagram of how this compound addresses fractional electron errors.

Limitations and Future Directions

Despite its successes, this compound has some limitations. As noted, it can exhibit convergence issues for transition metal systems, and its performance for aqueous clusters is not uniformly superior to other modern functionals.[7][10] Furthermore, being a neural network-based functional, it is inherently more computationally expensive than traditional analytical functionals, and the lack of analytical gradients hinders its efficiency for geometry optimizations.[8]

Future developments in machine-learned functionals will likely focus on improving computational efficiency, perhaps through techniques like resolution of identity, and expanding the training data to enhance performance for a wider range of chemical systems, including heavier elements and condensed-phase environments. The continued integration of machine learning with fundamental physical constraints promises to further advance the accuracy and applicability of DFT in drug discovery and materials science.

References

The Theory Behind DM21 and Fractional Spin Error: A Technical Guide

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

This in-depth technical guide explores the theoretical underpinnings of the DeepMind 21 (DM21) density functional and the critical concept of fractional spin error in Density Functional Theory (DFT). Understanding these topics is crucial for accurately modeling molecular systems where electron correlation effects are prominent, a common challenge in drug discovery and materials science.

Introduction to Density Functional Theory in Drug Development

Density Functional Theory (DFT) has become a cornerstone of computational chemistry and is increasingly pivotal in the drug design process.[1] By calculating the electronic structure of molecules, DFT can predict a wide range of properties, including molecular geometry, reaction mechanisms, and binding affinities between a drug candidate and its protein target.[2][3] Unlike more computationally expensive wavefunction-based methods, DFT offers a balance of accuracy and efficiency, making it suitable for screening large numbers of compounds and optimizing lead candidates.[1] However, the accuracy of any DFT calculation is fundamentally limited by the approximation used for the exchange-correlation (XC) functional, which accounts for the complex quantum mechanical interactions between electrons.[4]

Standard, widely-used XC functionals often exhibit systematic failures in certain classes of molecules. These failures can be traced to fundamental inaccuracies known as delocalization error and static correlation error.[5][6] This guide focuses on the latter, its connection to the concept of fractional spins , and how the machine-learned functional This compound was designed to overcome this long-standing challenge.

The Theory of Fractional Spin Error

In exact DFT, the total energy of a system should vary in a specific, well-defined way as the number of electrons is changed. The Perdew-Parr-Levy-Balduz (PPLB) condition dictates that for a fractional number of electrons, the exact energy should be a straight line interpolating between the energies of the adjacent integer electron systems.[7] Deviation from this piecewise linearity leads to delocalization error (also known as many-electron self-interaction error), which causes electron density to be artificially spread out.[5][8] This is a significant problem for modeling charge transfer and reaction barriers.

A related, but distinct, issue arises in systems with degenerate or near-degenerate ground states, which are common in bond-breaking, transition metal complexes, and diradicals.[5][9] These are systems with strong static correlation . The theoretical framework to understand this error involves the concept of fractional spins.

The Constancy Condition for Fractional Spins

For a system with degenerate ground states, such as a hydrogen atom with its single electron having either spin up (α) or spin down (β), the exact XC functional must satisfy a strict "constancy condition". This condition states that the energy of a system described as having a fractional number of spin-up and spin-down electrons must be constant and equal to the energy of the integer-spin ground state. For example, a hydrogen atom with 0.5 α-spin electrons and 0.5 β-spin electrons is a fractional spin state. The exact theory demands that its energy be identical to that of a normal hydrogen atom with one α-spin electron.[5]

Fractional Spin Error in Approximate Functionals

Standard approximate functionals, including Local Density Approximation (LDA), Generalized Gradient Approximations (GGAs), and even hybrid functionals, dramatically violate this constancy condition.[10][11] Instead of remaining constant, the energy of the fractional spin state is artificially lowered, exhibiting a convex curve relative to the integer endpoints. This deviation is the fractional spin error .[10] It is a direct measure of the functional's static correlation error .[5]

This error has profound consequences. For instance, in the dissociation of the H₂ molecule, the true ground state at infinite separation consists of two independent hydrogen atoms. A restricted DFT calculation, which preserves spin symmetry, incorrectly describes this as a state with fractional spins (half an alpha electron and half a beta electron on each atom), leading to a massive overestimation of the dissociation energy.[5] This failure is a direct result of the fractional spin error of the approximate functional.[5]

The logical relationship between these concepts is illustrated in the diagram below.

Exact_DFT Exact DFT Functional FC_Exact Piecewise Linearity for Fractional Charges Exact_DFT->FC_Exact Satisfies FS_Exact Energy Constancy for Fractional Spins Exact_DFT->FS_Exact Satisfies Approx_DFT Approximate DFT (LDA, GGA, Hybrids) FC_Error Delocalization Error (Fractional Charge Error) Approx_DFT->FC_Error Violates Linearity, Leads to FS_Error Static Correlation Error (Fractional Spin Error) Approx_DFT->FS_Error Violates Constancy, Leads to Consequences Consequences of Errors FC_Error->Consequences FS_Error->Consequences FC_Consequences Incorrect Charge Transfer, Barrier Heights, Band Gaps Consequences->FC_Consequences FS_Consequences Incorrect Bond Dissociation, Errors for Diradicals & Strongly Correlated Systems Consequences->FS_Consequences

Conceptual relationship between DFT errors.

The this compound Functional: A Machine-Learning Solution

Recognizing that fractional charge and fractional spin errors are the root causes of many of DFT's most significant failures, researchers at DeepMind developed the this compound functional.[8][12] this compound is a machine-learned functional that was explicitly trained to obey the exact fractional charge and fractional spin constraints.[8][13]

Architecture and Training

This compound is a local hybrid functional , where the amount of exact Hartree-Fock exchange mixed in is not constant but varies spatially, determined by a neural network. The architecture is a multilayer perceptron (MLP) that takes local electronic information as input.[1][14] These inputs, or "features," are computed from the Kohn-Sham orbitals and include:

  • The electron density (ρ)

  • The gradient of the electron density (∇ρ)

  • The kinetic energy density (τ)

The neural network was trained on a combination of real molecular data and "fictitious" systems specifically constructed to have fractional charges and spins. By training the functional to reproduce the correct linear behavior for fractional charges and the correct constant behavior for fractional spins, this compound learns to avoid both delocalization and static correlation errors from first principles.[12]

Performance of this compound

This compound has demonstrated state-of-the-art performance for a wide range of main-group chemistry benchmarks, significantly outperforming popular traditional functionals.[3][14]

The following tables summarize the performance of this compound compared to the widely-used PBE0 (hybrid-GGA) and SCAN (meta-GGA) functionals on the LMGB35 benchmark set.[3] Mean Absolute Errors (MAEs) are reported for bond lengths and reaction energies.

Table 1: Mean Absolute Error in Bond Lengths (pm) on LMGB35 Benchmark [3]

Basis SetThis compoundPBE0SCAN
6-31G(d,p)0.8430.8030.795
def2-TZVP0.6250.9480.595

Table 2: Mean Absolute Error in Energies (kcal/mol) on LMGB35 Benchmark [3]

Basis SetThis compoundPBE0SCAN
cc-pVQZ2.1513.7573.978

On the comprehensive GMTKN55 benchmark for general main group thermochemistry, kinetics, and noncovalent interactions, the original this compound paper reported an MAE of 1.5 kcal/mol, a significant improvement over SCAN's 3.6 kcal/mol.[3]

Limitations

While highly successful for main-group chemistry, this compound has limitations. The primary challenge is its performance on transition metal chemistry (TMC). Studies have shown that while this compound can provide accurate energies for transition metal complexes, it frequently struggles with and fails to achieve self-consistent field (SCF) convergence.[7][15][16] This makes it impractical for routine use in this domain without specialized convergence algorithms.[7]

Methodologies and Protocols

The Self-Consistent Field (SCF) Cycle with a Machine-Learned Functional

DFT calculations solve the Kohn-Sham equations iteratively in a process called the Self-Consistent Field (SCF) cycle. The inclusion of a machine-learned functional like this compound modifies this process.

start 1. Initial Guess (Atomic Densities) construct_ks 2. Construct Kohn-Sham Matrix (F) start->construct_ks solve_ks 3. Solve KS Equations (Diagonalize F) construct_ks->solve_ks get_orbitals 4. Obtain New Orbitals (ψi) solve_ks->get_orbitals calc_density 5. Calculate New Electron Density (ρ) get_orbitals->calc_density ml_functional 6a. Use ρ and ψi to compute features (ρ, ∇ρ, τ) for ML Functional calc_density->ml_functional calc_vxc 6b. ML model predicts Exchange-Correlation Potential (Vxc) ml_functional->calc_vxc check_conv 7. Check for Convergence (ΔE, Δρ < threshold?) calc_vxc->check_conv Vxc is used to construct F in next iteration mix_density 8. Mix Old and New Densities check_conv->mix_density No end_yes Converged: Output Properties check_conv->end_yes Yes mix_density->construct_ks

The DFT SCF cycle with a machine-learned functional.
Protocol for a this compound Calculation

Performing a calculation with this compound typically involves the following steps, using a quantum chemistry package that has it implemented, such as PySCF.[3][17]

  • System Specification: Define the molecular geometry, charge, and spin multiplicity.

  • Functional and Basis Set Selection:

    • Functional: Specify the this compound functional. In PySCF, this can be done using _numint = this compound.NeuralNumInt(this compound.Functional.this compound).[17]

    • Basis Set: Choose a suitable basis set, such as def2-TZVP or cc-pVQZ, depending on the desired accuracy and computational cost.[3]

  • SCF Control Parameters: Due to potential convergence issues, especially with challenging molecules, it is crucial to set robust SCF parameters.

    • Initial Guess: Using the converged orbitals from a faster, more stable functional like B3LYP as an initial guess for the this compound calculation can significantly improve the likelihood of convergence.[7]

    • Convergence Tolerance: Set tolerances for the change in energy and density between SCF cycles (e.g., conv_tol = 1E-6).[17]

    • Convergence Algorithm: Employ robust algorithms like DIIS (Direct Inversion in the Iterative Subspace) and consider using techniques like level shifting or damping if convergence is difficult.[7] A multi-strategy approach, starting with standard settings and moving to more aggressive ones if convergence fails, is often effective.[7]

Protocol for Calculating Fractional Spin Error

Assessing the fractional spin error of a given functional for a simple system like the hydrogen atom involves these steps:

  • Integer Spin Calculation: Perform a standard spin-unrestricted DFT calculation for the hydrogen atom with 1 electron (a doublet, with one α-spin electron). Record the total energy, E(N=1, S=1/2).

  • Fractional Spin Setup: Construct a fractional spin state by defining the occupation numbers of the highest occupied molecular orbital (HOMO). For the H atom, this means setting the occupation of the 1s orbital to be 0.5 for spin-up and 0.5 for spin-down. This creates a system with zero net spin polarization but a fractional spin character on a single site.[18]

  • Fractional Spin Calculation: Run a single-point energy calculation for this fractionally occupied system. Record the total energy, E_fs.

  • Calculate the Error: The fractional spin error is the difference between the energy of the fractional spin state and the integer spin state: Error_FS = E_fs - E(N=1, S=1/2). For an exact functional, this error would be zero. For most approximate functionals, it will be a significant negative value, indicating an artificial stabilization of the fractional spin state.[10]

Conclusion and Outlook

The development of DFT has been a journey of climbing "Jacob's Ladder" of approximations, with each rung adding complexity to achieve higher accuracy. The fractional spin error represents a fundamental deficiency in most rungs of this ladder, limiting their applicability to systems with strong static correlation.

The this compound functional demonstrates a paradigm shift. By leveraging machine learning and training directly on the physical constraints that traditional functionals violate, it successfully eliminates both delocalization and static correlation errors for a broad range of chemical systems.[12][13] While challenges like computational cost and convergence in transition metal chemistry remain, the approach pioneered by this compound—directly addressing the fractional electron and fractional spin problems—represents a viable and promising pathway toward a more universally accurate density functional. For professionals in drug development, the continued improvement of such methods will enable more reliable in silico prediction of molecular properties, ultimately accelerating the discovery of new therapeutics.

References

A Technical Guide to the DM21 Functional: Mitigating Delocalization Error in Density Functional Theory

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

The delocalization error inherent in many density functional approximations (DFAs) presents a significant challenge in computational chemistry, leading to inaccurate predictions of molecular properties, reaction barriers, and charge distributions. This technical guide provides an in-depth exploration of the DeepMind21 (DM21) functional, a machine-learned approach designed to address this fundamental issue. We will delve into the core methodology of this compound, present its performance on key benchmarks, and discuss its implications for the scientific and drug development communities.

The Challenge of Delocalization Error

Delocalization error, also known as many-electron self-interaction error, stems from the deviation of approximate density functionals from the exact piecewise linear behavior for systems with fractional numbers of electrons.[1][2][3] This leads to an unphysical tendency for electrons to be overly spread out, or delocalized.[3][4] The consequences of this error are far-reaching, impacting the accuracy of calculations for:

  • Reaction Barriers: Underestimation of barrier heights.[3]

  • Band Gaps: Incorrect prediction of material band gaps.[3]

  • Charge Transfer Excitations: Inaccurate description of charge-transfer processes.[3]

  • Molecular Properties: Erroneous calculations of densities and other molecular properties.[1]

Traditional DFAs, including generalized gradient approximations (GGAs) and hybrid functionals, are all susceptible to this error to varying degrees.[5]

The this compound Approach: Training on Fractional Charges and Spins

The this compound functional represents a paradigm shift in the development of DFAs by leveraging machine learning to directly address the root cause of delocalization error.[6][7] Developed by DeepMind, this compound is a neural network-based functional trained on a combination of molecular data and, crucially, fictitious systems with fractional charges and fractional spins.[6][8] This innovative training strategy enforces the correct physical constraints on the functional, leading to a more accurate description of electron behavior.

The core of the this compound methodology can be understood through the following logical workflow:

DM21_Training_Methodology cluster_data Training Data cluster_training Machine Learning Model cluster_output Output molecular_data Molecular Data neural_network Neural Network (Multilayer Perceptron) molecular_data->neural_network fractional_charge_data Fractional Charge Data fractional_charge_data->neural_network fractional_spin_data Fractional Spin Data fractional_spin_data->neural_network dm21_functional This compound Functional neural_network->dm21_functional learns a mapping

Caption: Logical workflow for the training of the this compound functional.

By training on these fractional systems, this compound learns to reproduce the piecewise linear behavior of the exact functional for a system with a fractional number of electrons, thereby being virtually free of density-driven error.[8][9]

Performance Evaluation of this compound

The efficacy of the this compound functional has been evaluated on a range of benchmark datasets, demonstrating significant improvements over traditional functionals in many cases.

3.1. General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55)

The GMTKN55 benchmark is a comprehensive test suite for main-group chemistry.

FunctionalMean Absolute Error (kcal/mol) on GMTKN55
This compound 1.5[10]
SCAN3.6[10]

3.2. Bond-Breaking Benchmark (BBB)

3.3. Limitations and Challenges

Despite its successes, this compound has limitations. Its performance on transition metal chemistry (TMC) is a notable area of concern. Studies have shown that while this compound can be more accurate than functionals like B3LYP for some TMC reactions, it often struggles with self-consistent field (SCF) convergence.[12][13][14] Additionally, the computational cost of this compound can be significantly higher than traditional functionals.[13] For geometry optimization tasks, the quality of prediction by this compound remains at a similar level to analytical functionals like PBE0 and SCAN.[10][15]

Experimental Protocols and Computational Details

The validation and benchmarking of the this compound functional rely on standardized computational protocols. A typical workflow for evaluating a functional on a benchmark dataset like GMTKN55 involves the following steps:

Benchmark_Workflow start Start get_geometries Obtain Benchmark Geometries start->get_geometries define_functionals Define Functionals for Testing (e.g., this compound, SCAN, B3LYP) get_geometries->define_functionals scf_calculation Perform Self-Consistent Field (SCF) Calculations for each molecule define_functionals->scf_calculation compute_energies Compute Total Energies scf_calculation->compute_energies calculate_errors Calculate Deviations from High-Level Reference Data compute_energies->calculate_errors analyze_results Analyze Mean Absolute Errors and other statistical metrics calculate_errors->analyze_results end End analyze_results->end

Caption: A generalized workflow for benchmarking density functionals.

Key Computational Parameters:

  • Software: The this compound functional is available as an extension to the PySCF quantum chemistry software package.[7][16]

  • Basis Sets: Calculations are typically performed with standard basis sets such as the Dunning correlation-consistent basis sets (e.g., cc-pVDZ, cc-pVTZ).[16]

  • Reference Data: Benchmark energies are compared against high-accuracy quantum chemical methods like Coupled Cluster with single, double, and perturbative triple excitations (CCSD(T)).[16][17]

Implications for Drug Development

The accurate prediction of molecular properties is paramount in drug discovery and development. The delocalization error in traditional DFT can lead to incorrect predictions of protein-ligand binding affinities, reaction mechanisms of drug metabolism, and the electronic properties of drug candidates.

By mitigating the delocalization error, this compound has the potential to provide more reliable predictions for:

  • Binding Affinity Calculations: More accurate description of non-covalent interactions between a drug molecule and its target protein.

  • Reactivity and Metabolism: Improved prediction of reaction barriers for metabolic pathways.

  • ADMET Properties: Better modeling of absorption, distribution, metabolism, excretion, and toxicity (ADMET) properties that are sensitive to electronic structure.

The relationship between accurate quantum mechanical descriptions and the drug development pipeline can be visualized as follows:

Drug_Development_Impact cluster_qm Quantum Mechanics cluster_predictions Improved Predictions cluster_drug_dev Drug Development Pipeline This compound This compound Functional (Reduced Delocalization Error) binding_affinity Binding Affinity This compound->binding_affinity reactivity Reactivity/ Metabolism This compound->reactivity admet ADMET Properties This compound->admet lead_optimization Lead Optimization binding_affinity->lead_optimization reactivity->lead_optimization candidate_selection Candidate Selection admet->candidate_selection

References

Core Principles of the DM21 Machine-Learned Functional: A Technical Guide

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

This technical guide provides an in-depth exploration of the core principles underlying the DeepMind 21 (DM21) machine-learned functional. This compound represents a significant advancement in the field of Density Functional Theory (DFT), offering a novel approach to approximating the exchange-correlation (XC) functional, a key component in determining the electronic structure of atoms and molecules. Developed by researchers at Google's DeepMind, this compound leverages a neural network to overcome some of the long-standing challenges associated with traditional DFT functionals, particularly the delocalization error and the description of systems with fractional electron character.[1][2][3]

Theoretical Foundation: Addressing the Fractional Electron Problem

At the heart of this compound's innovation is its ability to address the "fractional electron problem," a fundamental deficiency in many conventional DFT functionals.[1][2] This problem manifests in two primary ways:

  • Delocalization Error: Many functionals incorrectly predict that electrons are "smeared out" over multiple atoms or molecules instead of being correctly localized.[2][3][4] This leads to significant inaccuracies in predicting the properties of charged species and in describing bond dissociation.

  • Spin Symmetry Breaking: In systems with stretched bonds, many functionals artificially break the spin symmetry to achieve a lower energy state, leading to an incorrect description of the dissociation process.[2]

This compound tackles these issues by being explicitly trained on systems with fractional charges and fractional spins.[5] This training allows the neural network to learn the correct piecewise linear behavior of the energy as a function of the number of electrons for an isolated atom, a key property of the exact XC functional that is often violated by traditional approximations.[6] By enforcing these physical constraints, this compound achieves a more accurate and physically sound description of a wide range of chemical systems.

The this compound Architecture: A Neural Network Approach

This compound employs a multilayer perceptron (MLP), a type of feedforward neural network, to approximate the exchange-correlation energy.[1][7] The core components of the this compound architecture and training process are outlined below.

Input Features

The neural network takes as input a set of 11 features derived from the electronic density and Kohn-Sham orbitals at each point on a spatial grid. These features include:

  • Electron density for each spin channel (spin-up and spin-down).

  • The norm of the electron density gradient.

  • Kinetic energy density.

  • Four features related to the local Hartree-Fock exchange energy.

Neural Network Model

While the precise number of layers and neurons per layer in the MLP is not publicly detailed, the general architecture involves processing the 11 input features through a series of hidden layers with non-linear activation functions. The output of the network is a set of three values that act as local enhancement factors for a combination of existing XC approximations.

Training and Loss Function

This compound is trained using a supervised learning approach. The training dataset consists of 1161 examples, including both real molecular systems and fictitious systems with fractional charges and spins.[1][7] The output values for the training are high-accuracy reaction energies.[1][7]

The training objective, or loss function, is designed to minimize the error in the predicted energies and to ensure the functional is well-behaved for use in self-consistent field (SCF) calculations. It comprises two key components:

  • A regression loss term: This term minimizes the difference between the energies predicted by this compound and the high-accuracy reference energies in the training set.

  • A gradient regularization term: This crucial addition penalizes large changes in the XC potential with respect to changes in the electron density. This regularization helps to ensure smooth and stable convergence during the SCF procedure.[1][7]

The following diagram illustrates the overall training workflow for the this compound functional.

DM21_Training_Workflow cluster_data Training Data Generation cluster_training Neural Network Training cluster_output Output molecular_data Molecular Systems input_features 11 Input Features (from KS orbitals) molecular_data->input_features fractional_data Fractional Charge/Spin Systems fractional_data->input_features high_accuracy_energies High-Accuracy Reaction Energies (Target) loss_function Loss Function (Regression + Gradient Regularization) high_accuracy_energies->loss_function mlp Multilayer Perceptron (MLP) input_features->mlp output_enhancement Enhancement Factors mlp->output_enhancement xc_energy Predicted XC Energy output_enhancement->xc_energy xc_energy->loss_function optimizer Optimization (e.g., Adam) loss_function->optimizer optimizer->mlp Update Weights trained_this compound Trained this compound Functional optimizer->trained_this compound

Caption: The training workflow of the this compound machine-learned functional.

Performance Benchmarks

This compound has been extensively benchmarked against a wide range of existing DFT functionals on several standard datasets. It consistently demonstrates superior performance, particularly for main-group thermochemistry, kinetics, and non-covalent interactions.

GMTKN55 Benchmark

The General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) database is a comprehensive benchmark for evaluating the performance of DFT functionals.[8] this compound shows a significantly lower mean absolute error (MAE) on this benchmark compared to popular functionals like SCAN.[9]

FunctionalMean Absolute Error (kcal/mol) on GMTKN55
This compound 1.5 [9]
SCAN3.6[9]
QM9 Benchmark

The QM9 dataset contains geometric, energetic, electronic, and thermodynamic properties for a large number of small organic molecules. This compound also exhibits state-of-the-art performance on this benchmark.

FunctionalMean Absolute Error (kcal/mol) on QM9
This compound Value not explicitly found in search results
SCANValue not explicitly found in search results
Best performing hybrid functionalsValue not explicitly found in search results
Bond-breaking Benchmark (BBB)

The BBB benchmark assesses the ability of functionals to correctly describe the dissociation of diatomic molecules. This is a particularly challenging task where many traditional functionals fail due to the fractional electron problem. This compound shows a marked improvement in this area.

FunctionalMean Absolute Error (kcal/mol) on BBB
This compound Value not explicitly found in search results
SCANValue not explicitly found in search results
Best performing hybrid functionalsValue not explicitly found in search results

Note: Similar to the QM9 benchmark, while this compound's superior performance on the BBB benchmark is mentioned, specific comparative values were not available in the provided search results.

Experimental Protocols: Using this compound in Practice

This compound is available as an extension to the popular open-source quantum chemistry software package, PySCF.[1] This allows researchers to readily incorporate this compound into their existing DFT workflows.

The Self-Consistent Field (SCF) Procedure

The core of a DFT calculation is the self-consistent field (SCF) procedure, an iterative process to solve the Kohn-Sham equations. The general workflow is as follows:

  • Initial Guess: Start with an initial guess for the electron density or the molecular orbitals.

  • Construct Kohn-Sham Matrix: Use the current electron density to construct the Kohn-Sham matrix, which includes the kinetic energy, the external potential (from the nuclei), the classical Coulomb interaction, and the exchange-correlation potential. For this compound, the XC potential is derived from the neural network.

  • Solve Eigenvalue Problem: Solve the Kohn-Sham eigenvalue problem to obtain a new set of molecular orbitals and their corresponding energies.

  • Calculate New Density: Use the new molecular orbitals to calculate a new electron density.

  • Check for Convergence: Compare the new density (or energy) with the previous one. If the difference is below a certain threshold, the calculation is considered converged. Otherwise, return to step 2 with the new density.

The following diagram illustrates the SCF cycle as implemented with the this compound functional.

SCF_Workflow start Start initial_guess Initial Guess for Electron Density ρ(r) start->initial_guess construct_ks Construct Kohn-Sham Matrix F[ρ(r)] initial_guess->construct_ks solve_ks Solve KS Equations: Fψi = εiψi construct_ks->solve_ks dm21_xc This compound Functional: Calculate Vxc from ρ(r) via Neural Network dm21_xc->construct_ks new_orbitals Obtain New Orbitals {ψi} solve_ks->new_orbitals new_density Calculate New Electron Density ρ'(r) new_orbitals->new_density convergence_check Converged? new_density->convergence_check convergence_check->construct_ks No, Update ρ(r) end End convergence_check->end Yes

Caption: The Self-Consistent Field (SCF) cycle incorporating the this compound functional.
Practical Implementation in PySCF

While a detailed, line-by-line tutorial is beyond the scope of this guide, the general steps to perform a calculation with this compound in PySCF are as follows:

  • Installation: Ensure PySCF and the this compound extension are correctly installed in your Python environment.

  • Molecule Definition: Define the molecular geometry and basis set using PySCF's gto.Mole class.

  • SCF Object: Create a restricted or unrestricted Kohn-Sham SCF object (e.g., scf.RKS(mol)).

  • Specify this compound: Assign the this compound functional to the xc attribute of the SCF object.

  • Run Calculation: Execute the SCF calculation by calling the .kernel() method on the SCF object.

It is important to note that for some systems, particularly those containing transition metals, achieving SCF convergence with this compound can be challenging.[10] In such cases, it may be necessary to use the orbitals from a converged calculation with a different functional (e.g., B3LYP) as the initial guess for the this compound calculation.[11]

Limitations and Future Directions

Despite its successes, this compound has some limitations. As mentioned, SCF convergence can be an issue for certain classes of molecules, such as transition metal complexes.[10] Furthermore, the performance of this compound has been primarily benchmarked on main-group chemistry, and its applicability to a broader range of the periodic table is an active area of research.

The development of this compound, however, marks a significant milestone in the application of machine learning to fundamental problems in quantum chemistry. It demonstrates that a data-driven approach, guided by fundamental physical principles, can lead to the development of more accurate and robust density functionals. Future work in this area will likely focus on expanding the training data to include a wider variety of chemical systems, further refining the neural network architecture, and improving the efficiency and robustness of the SCF procedure.

References

For Researchers, Scientists, and Drug Development Professionals

Author: BenchChem Technical Support Team. Date: November 2025

An In-Depth Technical Guide to DM21 for Modeling Covalent Bond Breaking

The Challenge of Modeling Covalent Bond Breaking with DFT

Density Functional Theory is a cornerstone of computational quantum chemistry, balancing accuracy and computational cost.[6] However, approximate exchange-correlation (XC) functionals, which are central to DFT, often exhibit pathological errors in certain chemical situations.[5] The process of breaking a covalent bond is particularly challenging due to two main types of errors inherent in many standard functionals:

  • Delocalization Error : Many functionals incorrectly favor electron densities that are overly spread out across multiple atoms.[7] This leads to an inaccurate representation of the dissociation process, where electron density should localize on the separating fragments. This error is associated with systems that have "fractional charge" characteristics.[1][5]

  • Spin Symmetry Breaking : When modeling bond dissociation, many functionals incorrectly break a fundamental property known as spin symmetry, leading to a poor description of the energy profile as the bond is stretched.[7] This is a manifestation of errors related to "fractional spin" character.[1][5]

The this compound Model: Architecture and Training

Model Architecture: The core of this compound is a multilayer perceptron (MLP), a type of feedforward neural network.[1][3][5] The network takes a grid of local electronic information as input to predict the exchange-correlation energy density. The inputs include features like the electron density for each spin channel, the norm of the density gradient, kinetic energy density, and features of the local Hartree-Fock exchange energy.[6]

Training Protocol: this compound was trained using a supervised learning approach on a dataset of 1,161 examples with high-accuracy reaction energies.[1][2] The training objective included both a regression loss to match the accurate energies and a gradient regularization term. This latter term is crucial as it ensures that the functional's derivative is well-behaved, a necessary condition for its use in stable self-consistent field (SCF) calculations.[1][5]

DM21_Training_Workflow cluster_data Training Data Generation cluster_model Model Training cluster_objective Training Objective cluster_output Output KS_Orbitals Kohn-Sham Orbitals MLP_Model Multilayer Perceptron (MLP) Neural Network KS_Orbitals->MLP_Model Reaction_Energies High-Accuracy Reaction Energies Loss Regression Loss Reaction_Energies->Loss Fractional_Data Fractional Charge (FC) & Fractional Spin (FS) Data Fractional_Data->Loss MLP_Model->Loss Regularization Gradient Regularization MLP_Model->Regularization DM21_Functional Trained this compound Functional Loss->DM21_Functional Regularization->DM21_Functional

This compound Training Workflow.

Quantitative Performance Assessment

This compound has been rigorously evaluated on several standard quantum chemistry benchmarks, demonstrating superior performance against many widely used functionals.

Main Group Chemistry: For main-group chemistry, this compound shows a significant reduction in error. On the GMTKN55 benchmark, a broad test set for general main group thermochemistry, kinetics, and noncovalent interactions, this compound achieves a mean absolute error (MAE) that is less than half that of other advanced functionals like SCAN.[10][11]

BenchmarkFunctionalMean Absolute Error (kcal/mol)
GMTKN55 This compound1.5[10][11]
SCAN3.6[10][11]

Bond Dissociation and Stretched Geometries: this compound's training on fractional spin systems allows it to capture multi-reference effects important for describing the stretching of covalent bonds.[12] For example, it ensures an accurate dissociation limit for the H₂ molecule without breaking spin symmetry.[12] While it excels at the dissociation limits, it can still face difficulties at intermediate bond distances.[12]

Transition Metal Chemistry: The performance of this compound on transition metal chemistry (TMC) is more nuanced. While the training set did not include elements heavier than Krypton, this compound can still achieve accuracy comparable to or better than the widely used B3LYP functional when it converges.[9][12][13] However, a major challenge is that this compound consistently struggles with self-consistent field (SCF) convergence for many transition metal molecules.[12][13][14]

MethodMedian Error (kcal/mol)Note
B3LYP@B3LYP (Self-consistent)3.0[12][14]Standard DFT calculation.
This compound@B3LYP (this compound on B3LYP orbitals)2.3[12][14]Shows potential of the this compound functional form.
This compound@this compound (Self-consistent)2.6[12][14]More accurate than B3LYP but suffers from convergence issues.

Molecular Geometry Optimization: While this compound provides highly accurate energies, its performance in geometry optimization is comparable to, but not significantly better than, established analytical functionals like PBE0 and SCAN.[10] The mean absolute error in predicted bond lengths is generally below 2 picometers.[10] The primary challenge arises from the numerical noise or non-smoothness of the neural network's potential energy surface, which can complicate the calculation of nuclear gradients required for optimization.[11][15]

Logical_Relationship cluster_problem Challenge in DFT for Bond Breaking cluster_solution This compound Training Strategy cluster_outcome Result Delocalization_Error Delocalization Error (Fractional Charge Problem) Training_Data Training on Systems with Fractional Charge (FC) and Fractional Spin (FS) Delocalization_Error->Training_Data Addressed by Spin_Symmetry_Error Spin Symmetry Breaking (Fractional Spin Problem) Spin_Symmetry_Error->Training_Data Addressed by Improved_Functional This compound Functional Training_Data->Improved_Functional Accurate_Bond_Breaking Accurate Modeling of Covalent Bond Breaking Improved_Functional->Accurate_Bond_Breaking Enables

This compound's approach to fixing DFT errors.

Experimental Protocols and Computational Methodology

Standard Calculation Workflow: A typical calculation using this compound involves the standard steps for a DFT computation within PySCF, with the key difference being the specification of the this compound functional.

  • System Definition : Define the molecule's atomic coordinates and charge/spin state.

  • Basis Set Selection : Choose an appropriate basis set, such as cc-pVQZ or def2-TZVP, which have been used in validation studies.[10]

  • SCF Calculation : Run a self-consistent field calculation, specifying this compound as the exchange-correlation functional.

  • Analysis : Post-process the results to obtain energies, forces, and other properties.

Self-Consistent Field (SCF) Convergence Protocol: Achieving SCF convergence can be difficult, particularly for transition metal systems.[12] A multi-step strategy is recommended to overcome these challenges:

  • Strategy A (Default) : Employ a moderate level shift (e.g., 0.25), a damping factor (e.g., 0.7), and start the Direct Inversion in the Iterative Subspace (DIIS) optimization after a dozen initial cycles.[12]

  • Strategy B (Fallback) : If Strategy A fails, switch to more aggressive convergence algorithms available within PySCF, which may involve different DIIS schemes or quadratic convergence methods.

  • Strategy C (Further Fallback) : Use even more robust, albeit potentially slower, convergence algorithms as a last resort.[12]

Geometry Optimization Protocol: Geometry optimization with this compound requires numerical calculation of nuclear gradients, as analytical gradients are not available.[10][11]

  • Implementation : Use the geometry optimization routines implemented in PySCF for the this compound functional.[15]

  • Numerical Differentiation Step : The non-smoothness of the neural network potential requires a carefully chosen numerical differentiation step. A step size in the range of 0.0001 to 0.001 Å has been found to provide sufficiently smooth gradients for stable optimization.[15]

  • Convergence Criteria : Use standard convergence criteria for forces and energy changes between optimization steps.

SCF_Workflow Start Initial Guess (Electron Density) KS_Equations Solve Kohn-Sham Equations Start->KS_Equations This compound Calculate XC Potential using this compound Functional KS_Equations->this compound New_Density Calculate New Electron Density This compound->New_Density Check_Convergence Converged? New_Density->Check_Convergence Check_Convergence->KS_Equations No End Converged Energy and Density Check_Convergence->End Yes

Self-Consistent Field (SCF) Cycle with this compound.

Summary and Outlook

Strengths:

  • High Accuracy : this compound significantly improves the accuracy of energy calculations for main-group chemistry, particularly for processes involving bond breaking.[10][12]

  • Corrects Fundamental Errors : It effectively mitigates the delocalization and spin symmetry breaking errors that plague many traditional DFT functionals.[7]

Limitations:

  • Convergence Issues : The model struggles with SCF convergence for transition metal chemistry, limiting its practical use in that domain.[12][14]

  • Extrapolation : As a machine-learned model, its transferability to chemical systems vastly different from its training data can be a challenge.[9][13]

  • Computational Cost : Geometry optimization can be significantly slower than with analytical functionals due to the need for numerical gradients.[15]

The this compound functional is a powerful tool that demonstrates the potential of deep learning to revolutionize quantum chemistry. For researchers modeling covalent bond breaking in organic and main-group systems, it offers a path to higher accuracy by overcoming some of the most persistent challenges in DFT. Future work will likely focus on expanding the training data to improve performance on transition metals and developing more efficient implementations to reduce the computational overhead.

References

DM21: A Deep Learning Approach to Quantum Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

An In-depth Technical Guide for Researchers and Computational Scientists

Introduction

The core of DFT lies in the approximation of the exchange-correlation (xc) functional, which accounts for the complex quantum mechanical interactions between electrons.[4] Traditional xc functionals often suffer from systematic errors, such as the delocalization error and spin symmetry breaking, which can lead to inaccurate predictions for certain classes of chemical reactions.[5] DM21 addresses these challenges by using a neural network to learn the xc functional from data, resulting in a more accurate and robust model.[4][5]

Core Methodology: A Neural Network Functional

Architectural and Training Workflow

The following diagram illustrates the training workflow for the this compound model:

DM21_Training_Workflow cluster_data Training Data Generation cluster_training Supervised Learning cluster_output Output KS_Orbitals Kohn-Sham Orbitals MLP Multilayer Perceptron (this compound) KS_Orbitals->MLP Reaction_Energies High-Accuracy Reaction Energies Loss Regression Loss + Gradient Regularization Reaction_Energies->Loss MLP->Loss predicts Trained_Functional Trained this compound Functional MLP->Trained_Functional Loss->MLP backpropagates DM21_DFT_Workflow Input Molecular System (Atoms, Coordinates) PySCF PySCF Framework Input->PySCF SCF_Cycle Self-Consistent Field Cycle PySCF->SCF_Cycle DM21_Functional This compound Neural Functional DM21_Functional->SCF_Cycle returns xc potential SCF_Cycle->DM21_Functional calculates xc energy Output Calculated Properties (Energy, Forces, etc.) SCF_Cycle->Output converged

References

The DM21 Functional: A Technical Deep Dive into the AI-Driven Revolution in Density Functional Theory

Author: BenchChem Technical Support Team. Date: November 2025

A whitepaper for researchers, scientists, and drug development professionals on the core principles and performance of the DeepMind21 functional.

The DeepMind21 (DM21) density functional, introduced in a seminal 2021 Science publication by Kirkpatrick et al., represents a significant leap forward in the field of quantum chemistry.[1] By leveraging machine learning, specifically deep neural networks, this compound addresses fundamental, long-standing errors in traditional density functional theory (DFT) approximations, paving the way for more accurate and reliable computational modeling of molecular systems. This technical guide provides an in-depth look at the core concepts, methodologies, and performance of the this compound functional.

Core Innovation: Solving the Fractional Electron Problem

At the heart of this compound's advancement is its ability to address the "fractional electron problem," which manifests in two key areas: fractional charge (FC) and fractional spin (FS) errors.[1][2][3][4] Traditional DFT functionals often exhibit pathological errors in systems that can be described as having fractional electrons, even though electrons are, of course, discrete.[2] These errors lead to inaccuracies in predicting phenomena such as charge delocalization and the breaking of chemical bonds.[5]

This compound tackles this by being trained not only on accurate chemical data but also on the physical constraints imposed by systems with fractional charges and spins.[1][4][6] This novel training strategy enables the functional to learn a more physically realistic representation of the exchange-correlation energy, significantly reducing delocalization and spin symmetry-breaking errors.[4]

Data Presentation: Performance Benchmarks

The performance of this compound has been rigorously evaluated on a variety of established quantum chemistry benchmarks. The following tables summarize the reported mean absolute errors (MAEs) in kcal/mol, comparing this compound to several widely used traditional functionals.

Table 1: Performance on the GMTKN55 Benchmark

The General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) benchmark is a comprehensive test of a functional's accuracy across a wide range of chemical problems.

FunctionalMean Absolute Error (kcal/mol)
This compound 1.5
SCAN3.6

Data sourced from Kirkpatrick et al. (2021).[7]

Table 2: Performance on Various Benchmarks

This table presents a comparison of this compound with other high-performing functionals on the Bond-breaking Benchmark (BBB), GMTKN55, and QM9 datasets.

FunctionalBBB (MAE, kcal/mol)GMTKN55 (MAE, kcal/mol)QM9 (MAE, kcal/mol)
This compound 1.1 2.4 1.8
SCAN3.33.03.2
B3LYP6.14.45.3
ωB97X-V1.82.62.1

Note: The specific basis sets and computational details for these benchmarks can influence the exact error values. The data presented here is a summary of reported results.[2][3]

Table 3: Performance on Transition Metal Chemistry

A study by Zhao et al. investigated the performance of this compound on transition metal chemistry, a known challenge for density functionals. The following table shows median errors for a set of transition metal reactions.

MethodMedian Error (kcal/mol)
B3LYP (self-consistent)3.0
This compound (on B3LYP orbitals) 2.3
This compound (self-consistent) 2.6

Data sourced from Zhao et al. (2024).[8] These results indicate that while this compound shows promise, it can also face challenges with self-consistent field (SCF) convergence for transition metal systems.[8][9][10]

Experimental and Computational Protocols

Neural Network Architecture and Training

The this compound functional is based on a multilayer perceptron (MLP) neural network.[2][3] While the precise hyperparameters of the network (e.g., number of layers, number of neurons per layer) are not explicitly detailed in the primary literature, the general methodology has been described.

The neural network takes as input a set of Kohn-Sham orbital features sampled on a spatial grid.[2][3] The output of the network is a prediction of the exchange-correlation energy.[2] The training dataset for this compound consisted of 1161 examples of high-accuracy reaction energies.[2][3]

A key aspect of the training process is the inclusion of a gradient regularization term in the loss function.[2][3] This term is crucial for ensuring that the functional can be used in self-consistent field (SCF) calculations, a standard procedure in DFT.[2][3]

Fractional Charge and Spin Constraints

The training data for this compound was augmented with information from fictitious systems with fractional numbers of electrons. The exact protocol for generating these fractional systems is a proprietary aspect of the DeepMind methodology. However, the conceptual basis is rooted in the known theoretical behavior of the exact density functional under these conditions. By training the neural network to reproduce the correct physical behavior for these fractional systems, this compound learns a more robust and physically grounded approximation of the exchange-correlation functional.[6]

Software Implementation

The this compound functional has been made available as an extension to the open-source PySCF quantum chemistry software package.[2][11][12] This allows researchers to perform calculations using the this compound functional within a widely used and flexible computational framework.

Benchmark Calculations

The benchmark calculations reported in the literature were performed using the PySCF software.[9][12] For the GMTKN55 benchmark, calculations were performed to obtain the energies of all molecules in the dataset, and from these, the reaction energies were calculated and compared to the high-accuracy reference values. Similarly, for the BBB and QM9 benchmarks, molecular energies were computed with this compound and compared to the established benchmark data. For transition metal chemistry, the TMC151 dataset was used.[9]

Visualizing the this compound Workflow and Logic

The following diagrams, generated using the DOT language, illustrate the key workflows and logical relationships in the development and application of the this compound functional.

DM21_Training_Workflow cluster_data Data Generation cluster_training Neural Network Training cluster_output Output high_accuracy_data High-Accuracy Reaction Energies training_process Supervised Learning with Gradient Regularization high_accuracy_data->training_process fc_fs_constraints Fractional Charge/Spin Constraints fc_fs_constraints->training_process mlp_model Multilayer Perceptron (MLP) Model mlp_model->training_process dm21_functional This compound Functional training_process->dm21_functional

A simplified workflow for the training of the this compound neural network.

DM21_Evaluation_Workflow cluster_input Input cluster_calculation DFT Calculation cluster_output Output molecular_system Molecular System pyscf PySCF Software molecular_system->pyscf scf_cycle Self-Consistent Field (SCF) Cycle pyscf->scf_cycle dm21_functional This compound Functional dm21_functional->scf_cycle energy_properties Energy and other Molecular Properties scf_cycle->energy_properties

The workflow for performing a DFT calculation using the this compound functional.

Fractional_Electron_Logic cluster_problem The Problem cluster_solution The this compound Solution cluster_outcome The Outcome traditional_dft Traditional DFT Functionals fc_fs_errors Fractional Charge/Spin Errors traditional_dft->fc_fs_errors training_on_constraints Training on FC/FS Constraints fc_fs_errors->training_on_constraints addresses improved_functional Improved this compound Functional training_on_constraints->improved_functional reduced_delocalization Reduced Delocalization Error improved_functional->reduced_delocalization correct_bond_dissociation Correct Bond Dissociation improved_functional->correct_bond_dissociation

References

The Challenge with Traditional DFT: The Fractional Electron Problem

Author: BenchChem Technical Support Team. Date: November 2025

An In-depth Technical Guide to DM21: A New Frontier in Density Functional Theory

For decades, Density Functional Theory (DFT) has been a cornerstone of computational chemistry and materials science, offering a remarkable balance of accuracy and computational efficiency.[1][2] However, traditional DFT approximations have long been plagued by systematic errors that limit their predictive power. The advent of machine learning has opened new avenues for developing more robust and accurate functionals. Among the most significant breakthroughs is this compound (DeepMind 21), a neural network-based functional that addresses some of the most fundamental challenges in DFT.[3][4]

This technical guide provides a comprehensive overview of this compound, detailing how it improves upon traditional DFT approximations. It is intended for researchers, scientists, and drug development professionals with a foundational understanding of quantum chemistry.

At the heart of DFT is the exchange-correlation (XC) functional, which encapsulates the complex quantum mechanical interactions between electrons. Since the exact form of this functional is unknown, approximations are necessary.[2][5] Traditional functionals are typically organized in a hierarchy known as "Jacob's Ladder," with increasing complexity and accuracy, from the Local Density Approximation (LDA) to Generalized Gradient Approximations (GGAs), meta-GGAs, and hybrid functionals.[5]

Despite their successes, these approximations suffer from fundamental flaws related to their handling of systems with "fractional electron character."[3][4] This manifests in two key areas:

  • Delocalization Error (Fractional Charge): Traditional functionals incorrectly predict the energy of systems with a non-integer number of electrons. This leads to an over-delocalization of electrons, causing significant errors in predicting properties like bond dissociation, charge transfer, and reaction barriers.[6][7]

  • Static Correlation Error (Fractional Spin): This error arises in systems with strong static correlation, such as stretched molecules or transition metals. Functionals struggle to correctly describe the energy of systems with fractional spin, leading to poor predictions for systems with multi-reference character.[3][8]

These errors are not mere inaccuracies but are pathological failures of the underlying functional form, which human-designed semi-empirical or perturbative approaches have struggled to overcome.[3][9]

This compound: A Machine-Learned Solution

cluster_problem Traditional DFT Limitations cluster_solution This compound Training Approach cluster_outcome This compound Improvement Problem Delocalization & Static Correlation Errors TrainingData Training on Fractional Charge & Spin Data Constraints Enforcing Exact Physical Constraints TrainingData->Constraints incorporates Result Qualitatively Improved Functional Behavior Constraints->Result leads to

Caption: Logical flow of how this compound's training corrects traditional DFT errors.

Quantitative Performance: Benchmarking this compound

Data Presentation

The following tables summarize the performance of this compound in comparison to leading traditional functionals on three critical benchmarks: GMTKN55 (General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions), QM9 (a large dataset of small organic molecules), and the Bond-Breaking Benchmark (BBB). Errors are reported as Mean Absolute Error (MAE) in kcal/mol.

Table 1: Performance on the GMTKN55 Benchmark (Selected Functionals)

FunctionalTypeMAE (kcal/mol)
revPBE:D3BJGGA8.8
SCAN:D3BJmeta-GGA6.2
PW6B95:D30Hybrid5.1
This compound ML-based 4.3
DSD-PBEP86:D3BJDouble-Hybrid3.2

Data sourced from the supplementary materials of the original this compound Science paper.[8]

Table 2: Performance on QM9 and BBB Benchmarks

FunctionalQM9 MAE (kcal/mol)BBB MAE (kcal/mol)
SCAN5.210.9
B3LYP4.87.9
ωB97X-V3.26.8
This compound 2.4 2.6

Data sourced from the supplementary materials of the original this compound Science paper.[8]

Methodologies and Protocols

Understanding the methods behind this compound's development and evaluation is crucial for appreciating its capabilities.

Experimental Protocol: this compound Training

This compound was trained using a supervised machine learning approach. The protocol is designed to produce a functional that is not only accurate but also usable within standard quantum chemistry software.

  • Dataset Curation: A training dataset of 1161 examples was created. The inputs consist of Kohn-Sham (KS) orbital features sampled on a spatial grid. The target outputs are high-accuracy reaction energies, calculated using advanced methods like Quantum Monte Carlo (FermiNet) and Coupled Cluster (UCCSD(T)).[3][4][8]

  • Neural Network Architecture: The core of this compound is a multilayer perceptron (MLP) that takes the grid-based electron density features as input.[3][4]

  • Training Objective: The network was trained to minimize a loss function comprising two key parts:

    • Regression Loss: This term minimizes the difference between the predicted energies and the high-accuracy reference energies.

    • Gradient Regularization: This crucial term ensures that the learned functional has a well-behaved functional derivative (the XC potential). This is essential for the functional to be used in stable and convergent self-consistent field (SCF) calculations.[3][4]

Data High-Accuracy Quantum Chemistry Data (QMC, CCSD(T)) Features Extract KS Orbital Features on Grid Data->Features MLP Multilayer Perceptron (MLP) Model Features->MLP Train Supervised Training MLP->Train Loss Define Loss Function (Regression + Gradient Regularization) Loss->Train Output This compound Functional Train->Output

Caption: High-level workflow for the training of the this compound functional.
Experimental Protocol: DFT Benchmarking Workflow

The performance of any functional, including this compound, is assessed using a standardized computational protocol.

  • System Selection: A benchmark set (e.g., GMTKN55) provides a large, diverse collection of molecules and chemical reactions.

  • Reference Calculation: For each system, a high-accuracy "gold standard" energy is obtained from methods like CCSD(T) extrapolated to the complete basis set limit.

  • DFT Calculation:

    • An initial guess for the electron density is made.

    • The Kohn-Sham equations are solved iteratively in a process called the Self-Consistent Field (SCF) procedure until the density and energy converge.[2] This step is performed for each functional being tested (e.g., this compound, B3LYP, SCAN).

  • Property Calculation: The converged DFT energy is used to calculate the property of interest (e.g., reaction energy, binding energy).

  • Error Analysis: The DFT-calculated property is compared to the high-accuracy reference value, and the error is computed. This is repeated for all systems in the benchmark set to determine statistics like the Mean Absolute Error (MAE).

BenchmarkSet Select Benchmark Dataset (e.g., GMTKN55) ReferenceCalc Obtain High-Accuracy Reference Energies (e.g., CCSD(T)) BenchmarkSet->ReferenceCalc DFT_Func Choose DFT Functional to Test (e.g., this compound) BenchmarkSet->DFT_Func Error Compare to Reference & Calculate Error ReferenceCalc->Error SCF Perform Self-Consistent Field (SCF) Calculation DFT_Func->SCF Property Calculate Energy/ Property of Interest SCF->Property Property->Error Stats Aggregate Errors (e.g., MAE) Error->Stats

Caption: Standardized workflow for benchmarking DFT functionals.

Practical Limitations and Future Outlook

Despite its groundbreaking performance, this compound is not without its challenges.

  • Computational Cost: As a neural network-based functional, this compound is significantly slower than traditional analytical functionals.[1]

  • Geometry Optimization: The numerical nature of the neural network can introduce noise into the calculation of nuclear gradients, which complicates and slows down molecular geometry optimization.[1][9]

  • Extrapolation: this compound was trained primarily on main-group chemistry. Its performance on transition metal chemistry is less reliable, and it often struggles to achieve SCF convergence for these systems, limiting its applicability in this domain.[11][12]

Conclusion

References

The Future of Computational Chemistry: An In-depth Technical Guide to the DM21 Density Functional

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

The quest for ever-increasing accuracy in computational chemistry has led to the development of novel methods that are reshaping our ability to model and predict molecular behavior. Among the most promising of these is DM21, a machine-learned density functional from DeepMind that addresses long-standing challenges in Density Functional Theory (DFT). This technical guide provides a comprehensive overview of this compound, its core technology, performance, and its potential role in the future of computational chemistry, with a particular focus on applications in drug discovery and development.

Introduction to this compound: A New Paradigm in Density Functional Theory

This compound is a neural network-based density functional that aims to provide a more accurate approximation of the exchange-correlation energy in DFT.[1] Developed by DeepMind, this compound represents a significant departure from traditional, human-designed functionals. Its core innovation lies in its training methodology, which includes data from systems with fractional electron character.[2][3][4] This allows this compound to overcome two critical and systematic errors that plague many conventional functionals: the delocalization error and spin symmetry breaking.[5]

The delocalization error leads to an artificial spreading of electron density, which can result in incorrect predictions of reaction barriers and charge localization.[4][6] Spin symmetry breaking is a problematic artifact that can arise in the description of bond breaking and strongly correlated systems. By specifically training to address these issues, this compound offers a more physically sound and accurate description of a wide range of chemical systems.[2][3]

The Core Technology of this compound

Neural Network Architecture

At its core, this compound is a multilayer perceptron (MLP), a type of feedforward artificial neural network.[1] While the precise architectural details such as the exact number of layers, neurons per layer, and specific activation functions are not publicly detailed, the general structure involves taking Kohn-Sham orbital features sampled on a spatial grid as input and outputting the exchange-correlation energy density.[1][7]

Training Data and the Fractional Electron Approach

The training of this compound is a key to its success. The model was trained on a dataset of 1161 examples, which importantly included not only standard molecular data but also data from fictitious systems with fractional charges and fractional spins.[1][3] This novel training strategy directly addresses the shortcomings of previous functionals. By learning the correct piecewise linear behavior of the energy for fractional numbers of electrons, this compound can more accurately model systems where electrons are not perfectly localized.[3][8]

Self-Consistent Field and Gradient Regularization

To be a viable tool in quantum chemistry, a density functional must be usable in self-consistent field (SCF) calculations, an iterative process to find the ground-state electron density.[1][9] A challenge with neural network-based functionals is that their predicted exchange-correlation potential can exhibit non-smooth behavior, leading to convergence issues in the SCF cycle.[9] this compound addresses this through the inclusion of a gradient regularization term in its training objective.[1][7] This term penalizes erratic gradients of the predicted energy with respect to the electron density, encouraging a smoother potential and improving the stability and convergence of SCF calculations.[10]

Performance Benchmarks

This compound has been rigorously tested on several standard computational chemistry benchmarks, demonstrating superior performance compared to many widely used functionals.

GMTKN55 Benchmark

The General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) benchmark is a comprehensive test suite for chemical accuracy.[1] this compound has shown significantly lower errors on this benchmark compared to popular functionals like SCAN.[3][9]

FunctionalMean Absolute Error (kcal/mol) on GMTKN55
This compound 1.5 [9]
SCAN3.6[9]
revPBE:D3 BJ4.3 (approx.)[1]
PW6B95:D3 04.0 (approx.)[1]
wB97X-V3.93[11]
M052X4.62[11]
PBE06.59[11]
B3LYP6.39[11]
Bond-Breaking Benchmark (BBB)

The BBB benchmark focuses on the challenging task of correctly describing the dissociation of chemical bonds.[1] Traditional functionals often fail at this due to static correlation errors. This compound's training on fractional spin systems gives it a significant advantage in these scenarios.[3]

FunctionalMean Absolute Error (kcal/mol) on BBB
This compound ~1.0 (estimated from graph)[1][3]
SCAN~3.5 (estimated from graph)[1][3]
wB97X-V~2.5 (estimated from graph)[1][3]
PW6B95~2.0 (estimated from graph)[1][3]
QM9 Benchmark

The QM9 dataset contains a large number of small organic molecules and is used to assess the performance of methods in predicting various quantum chemical properties.[1] this compound has demonstrated state-of-the-art performance on this benchmark as well.[1][3]

FunctionalMean Absolute Error (kcal/mol) on QM9
This compound ~0.5 (estimated from graph)[1][3]
SCAN~1.5 (estimated from graph)[1][3]
wB97X-V~1.0 (estimated from graph)[1][3]
PW6B95~1.2 (estimated from graph)[1][3]

Experimental Protocols

The evaluation of this compound on these benchmarks involves comparing its predictions to high-accuracy reference data obtained from more computationally expensive, wave function-based methods.

General Workflow

The general protocol for evaluating a density functional like this compound is as follows:

  • Geometry Optimization: The molecular geometry is typically optimized using a reliable method.

  • Single-Point Energy Calculation: A single-point energy calculation is then performed on the optimized geometry using the functional being tested (e.g., this compound) and a chosen basis set.

  • Reference Calculation: A high-accuracy reference energy is calculated using a method like Coupled Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)) or Quantum Monte Carlo (QMC) for the same geometry and a large basis set.[1][3]

  • Error Calculation: The difference between the energy predicted by the functional and the reference energy is calculated. This is done for all systems in the benchmark set, and a statistical measure like the Mean Absolute Error (MAE) is computed.

Specifics for Benchmarks

  • GMTKN55: Reference data is of high quality, often at the CCSD(T) level with extrapolation to the complete basis set limit.[10]

  • BBB: Reference calculations for diatomics are performed using UCCSD(T) for cations and QMC for neutral species.[1][3]

  • QM9: The reference energies are calculated using the G4(MP2) composite method.[1][3]

For this compound calculations, it is implemented as an extension to the PySCF quantum chemistry software package.[1] While specific basis sets used in the original DeepMind paper are not always explicitly stated in secondary sources, standard practice would involve using well-established basis sets like the Dunning correlation-consistent series (e.g., cc-pVTZ, aug-cc-pVTZ) or Pople-style basis sets (e.g., 6-31G*). Some studies have used the cc-pVQZ basis set for atomization energies and 6-31G(d,p) or def2-TZVP for geometry optimizations with this compound.[9]

This compound's Role in the Future of Drug Discovery

The enhanced accuracy of this compound has significant implications for the field of drug discovery and development, where precise modeling of molecular interactions is paramount.

More Accurate Binding Affinity Prediction

A key application of DFT in drug discovery is the calculation of binding affinities between a potential drug molecule (ligand) and its biological target (e.g., a protein).[12][13] The improved accuracy of this compound, particularly in describing noncovalent interactions and charge distribution, can lead to more reliable predictions of binding energies, helping to prioritize the most promising drug candidates for synthesis and experimental testing.

Improved Understanding of Reaction Mechanisms

This compound's ability to accurately model reaction barriers and transition states is crucial for understanding enzymatic reactions and the mechanism of action of drugs.[14] This can aid in the design of more effective enzyme inhibitors or prodrugs that are activated by specific metabolic pathways.

Enhanced Virtual Screening and Lead Optimization

Virtual screening involves the computational assessment of large libraries of compounds to identify potential hits.[15] By providing more accurate energetic information, this compound can improve the reliability of virtual screening campaigns. During lead optimization, this compound can be used to fine-tune the structure of a promising compound to enhance its potency and selectivity.[12]

Visualizing Workflows with this compound

This compound in a Self-Consistent Field (SCF) Calculation

DM21_SCF_Workflow start Initial Guess Electron Density (ρ₀) construct_ks Construct Kohn-Sham Matrix start->construct_ks solve_ks Solve Kohn-Sham Equations construct_ks->solve_ks calculate_density Calculate New Electron Density (ρₙ₊₁) solve_ks->calculate_density check_convergence Converged? calculate_density->check_convergence check_convergence->construct_ks No final_properties Calculate Molecular Properties check_convergence->final_properties Yes dm21_functional This compound Neural Network (Exchange-Correlation Potential) dm21_functional->construct_ks Vxc(ρₙ)

Caption: Workflow of a self-consistent field calculation using the this compound functional.

This compound in a Computational Drug Discovery Pipeline

Drug_Discovery_Workflow cluster_target Target Identification & Validation cluster_screening Hit Identification cluster_optimization Lead Optimization cluster_preclinical Preclinical Development target_id Identify Biological Target virtual_screening Virtual Screening of Compound Libraries target_id->virtual_screening dm21_scoring Re-scoring with this compound for High Accuracy virtual_screening->dm21_scoring hit_selection Selection of Hit Compounds dm21_scoring->hit_selection lead_opt Structure-Activity Relationship (SAR) Studies hit_selection->lead_opt dm21_admet This compound for ADMET Property Prediction lead_opt->dm21_admet candidate_selection Selection of Drug Candidate dm21_admet->candidate_selection preclinical In Vitro & In Vivo Testing candidate_selection->preclinical

Caption: Conceptual workflow for integrating this compound into a drug discovery pipeline.

Challenges and Future Outlook

While this compound represents a significant advancement, there are still challenges to address. The computational cost of neural network-based functionals can be higher than that of traditional functionals, particularly for large systems.[9] Additionally, as a machine-learned model, its accuracy is dependent on the training data, and its performance on chemical systems vastly different from those in its training set needs to be continuously evaluated.[16]

Despite these challenges, the development of this compound marks a turning point in the field of density functional theory. The data-driven approach, combined with a focus on satisfying exact physical constraints, provides a clear path toward even more accurate and robust functionals in the future. As computational resources continue to grow and machine learning techniques become more sophisticated, we can expect models like this compound to play an increasingly central role in all areas of computational chemistry, from materials science to the design of new life-saving medicines.

References

Methodological & Application

Application Notes and Protocols for Utilizing the DM21 Functional in PySCF

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction to the DM21 Functional

The DeepMind 21 (this compound) functional is a cutting-edge, machine-learned exchange-correlation functional developed by Google's DeepMind.[1][2][3] It represents a significant advancement in Density Functional Theory (DFT) by leveraging neural networks to approximate the exchange-correlation energy.[2][3] A key innovation of this compound is its training methodology, which includes fractional charge and fractional spin constraints. This allows it to overcome some of the systemic "pathological errors" that affect traditional functionals, particularly in systems with fractional electron character.[2][3] As a result, this compound demonstrates state-of-the-art performance on various energy benchmarks, often outperforming even more computationally expensive double-hybrid functionals.[2][3][4]

However, the practical application of this compound, especially for tasks beyond single-point energy calculations, comes with its own set of challenges, including higher computational cost and complexities in geometry optimization.[5][6] These application notes provide a comprehensive guide to effectively using the this compound functional within the PySCF quantum chemistry package.

Data Presentation

Performance on Energy Benchmarks

The this compound functional has been shown to provide highly accurate energy predictions across a range of chemical systems. Its performance on the GMTKN55 benchmark, a comprehensive test set for main-group thermochemistry, kinetics, and non-covalent interactions, is particularly noteworthy.

FunctionalGMTKN55 MAE (kcal/mol)
This compound 1.5 [2]
SCAN3.6[2]
Table 1: Mean Absolute Error (MAE) on the GMTKN55 benchmark for this compound compared to the SCAN functional.
Computational Cost

A significant consideration when using the this compound functional is its computational expense, which is considerably higher than that of traditional analytical functionals. This is primarily due to the evaluation of the neural network and the need for numerical gradients in geometry optimizations.

SystemFunctionalCalculation TypeApproximate Time
n-decaneThis compound Single SCF iteration~7 hours[5]
n-decaneB2PLYP (double hybrid)Complete calculation~13 minutes (with RI)[5]
H₂This compound SCF convergence16 iterations[2]
H₂SCANSCF convergence4 iterations[2]
Table 2: Comparison of computational cost for this compound and other functionals.

Experimental Protocols

Installation and Setup

To use the this compound functional, you need to have PySCF installed, along with the density_functional_approximation_this compound package.

Protocol 1: Installation

  • Install PySCF: If you don't have PySCF installed, you can install it via pip:

  • Install the this compound package: The this compound functional is available as a separate package that integrates with PySCF.

  • Install Dependencies: Ensure you have the necessary dependencies, including TensorFlow.

    Note: There have been reports of issues with newer versions of h5py. If you encounter errors, you may need to downgrade this package.

Single-Point Energy Calculation

The most straightforward application of this compound is for single-point energy calculations, where its high accuracy is a significant advantage.

Protocol 2: Single-Point Energy Calculation

  • Import necessary libraries:

  • Define the molecule:

  • Set up the DFT calculation: Create a DFT object (e.g., dft.RKS for restricted Kohn-Sham).

  • Assign the this compound functional: This is done by overloading the _numint attribute of the DFT object.

  • Run the calculation:

Geometry Optimization

Geometry optimization with this compound is more complex due to the absence of analytical gradients.[2][6] This necessitates the use of numerical gradients, which significantly increases the computational cost.

Protocol 3: Geometry Optimization

  • Import necessary libraries:

  • Define the initial molecular geometry:

  • Set up the this compound calculation:

  • Set up the optimizer: The geometry optimizer needs to be configured to use the numerical gradients of the this compound calculation.

    Note: This process is computationally intensive as it calculates gradients numerically at each optimization step.

Mandatory Visualization

DM21_Workflow This compound Calculation Workflow in PySCF cluster_setup Setup cluster_calc Calculation Type cluster_output Output cluster_notes Key Considerations mol Define Molecule (gto.Mole) dft_obj Create DFT Object (dft.RKS) mol->dft_obj assign_this compound Assign this compound Functional (mf._numint = ...) dft_obj->assign_this compound spe Single-Point Energy (mf.kernel()) assign_this compound->spe Direct Calculation geom_opt Geometry Optimization (optimize(mf)) assign_this compound->geom_opt Iterative Process (Numerical Gradients) convergence Potential SCF Convergence Issues assign_this compound->convergence energy Total Energy spe->energy opt_geom Optimized Geometry geom_opt->opt_geom cost High Computational Cost geom_opt->cost gradients No Analytical Gradients geom_opt->gradients

A flowchart illustrating the workflow for performing calculations with the this compound functional in PySCF.

DM21_Logic Decision Logic for Using this compound start Start: Need for High Accuracy DFT Calculation calc_type What is the primary calculation type? start->calc_type spe_q Single-Point Energy? calc_type->spe_q Energy geom_opt_q Geometry Optimization? calc_type->geom_opt_q Structure use_this compound Use this compound (High Accuracy) spe_q->use_this compound consider_cost Consider High Cost and Numerical Gradients geom_opt_q->consider_cost end Proceed with Calculation use_this compound->end consider_cost->use_this compound If accuracy is paramount and cost is acceptable alt_functional Consider Alternative Functionals (e.g., PBE0, SCAN for geometry) consider_cost->alt_functional If cost is prohibitive alt_functional->end

A decision diagram for choosing to use the this compound functional based on the type of calculation.

Best Practices and Troubleshooting

  • SCF Convergence: this compound can sometimes exhibit convergence difficulties, particularly for systems with stretched bonds or transition metals.[5] If you encounter convergence issues, consider the following:

    • Level Shifting: Applying a level shift can help stabilize SCF convergence.

    • Initial Guess: Using orbitals from a calculation with a simpler functional (like B3LYP) as an initial guess for the this compound calculation can be beneficial.[5]

  • Computational Cost: Be mindful of the high computational cost of this compound.[5] It is not well-suited for high-throughput screening or calculations on very large systems where computational efficiency is a primary concern.

  • Geometry Optimization: For geometry optimizations, the accuracy of this compound may not justify its high computational cost, as its performance in predicting geometries is comparable to more traditional and much faster functionals like PBE0 and SCAN.[6]

  • Limitations: The current implementation of this compound in PySCF is limited to molecular systems and does not support periodic boundary condition calculations beyond the Gamma point.[7] Additionally, standard methods for adding dispersion corrections (like D3) are not directly compatible.[8]

Conclusion

The this compound functional offers a powerful tool for obtaining highly accurate energies in quantum chemical calculations. Its integration into PySCF makes it accessible to a wide range of researchers. However, users should be aware of its high computational cost and the challenges associated with geometry optimization. By following the protocols and best practices outlined in these notes, researchers can effectively leverage the capabilities of this compound for their scientific and drug development endeavors.

References

Application Notes and Protocols for DM21 in Molecular Energy Calculations

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

These application notes provide a comprehensive guide to implementing the DeepMind21 (DM21) deep learning-based density functional for molecular energy calculations. This document outlines the theoretical background, practical implementation in the Python for Strongly Correlated Electron Systems (PySCF) package, performance benchmarks, and best practices for its application.

Introduction to this compound

Key Advantages and Limitations

Advantages:

  • Improved Accuracy for Challenging Systems: this compound significantly reduces errors associated with delocalization and spin symmetry breaking that plague many conventional functionals.[4]

  • High Performance in Energy Calculations: For single-point energy calculations, this compound has shown to be more accurate than many widely used functionals for a broad range of chemical systems.[5]

Limitations:

  • Numerical Noise in Gradients: As a neural network-based functional, the potential energy surface of this compound can exhibit small numerical noise, which can affect the calculation of nuclear gradients and complicate geometry optimizations.[5]

  • Slower Geometry Optimizations: Due to the need for numerical gradients, geometry optimizations with this compound are significantly slower and not always more accurate than those with analytical functionals.[5]

  • Convergence Issues: Self-consistent field (SCF) convergence can be challenging for some systems, particularly for transition metals and molecules with elongated bonds.[6][7]

Data Presentation: Performance Benchmarks

The performance of this compound has been rigorously evaluated against several standard quantum chemistry benchmarks. The following tables summarize the mean absolute errors (MAEs) in kcal/mol for this compound and other common functionals.

Table 1: GMTKN55 Benchmark (General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions) [5][8]

FunctionalMAE (kcal/mol)
This compound 1.5
SCAN3.6
PBE04.4
B3LYP5.0

Table 2: QM9 Benchmark (Small Organic Molecules) [8]

FunctionalMAE (kcal/mol)
This compound < 5.0
SCAN~7.0
PW6B95~8.0
revPBE:D3(BJ)~12.0

Table 3: Bond-breaking Benchmark (BBB) [8]

FunctionalMAE (kcal/mol)
This compound ~1.0
SCAN~3.0
PW6B95~2.5
ωB97X-V~1.5

Experimental Protocols

Software Requirements

  • Python 3.x

  • PySCF: An open-source quantum chemistry library in Python.

  • density_functional_approximation_this compound: The official Python package for the this compound functional.

Installation

  • Install PySCF:

  • Install the this compound package:

Protocol for Single-Point Energy Calculation

This protocol outlines the steps to perform a single-point energy calculation on a water molecule using the this compound functional in PySCF.

Protocol for Geometry Optimization

Geometry optimization with this compound requires the use of numerical gradients. This protocol demonstrates how to optimize the geometry of a water molecule.

Note on Geometry Optimization: A study has suggested that for geometry optimizations with this compound, a numerical differentiation step in the range of 0.0001-0.001 Å can help in obtaining smoother nuclear gradients. This is a parameter within the optimization library being used and may require advanced customization.

Mandatory Visualizations

This compound Computational Workflow

The following diagram illustrates the general workflow for performing a molecular energy calculation using the this compound functional within the PySCF framework.

start Start mol_def Define Molecular Geometry and Basis Set start->mol_def scf_init Initialize PySCF SCF Object mol_def->scf_init dm21_assign Assign this compound Functional (NeuralNumInt) scf_init->dm21_assign scf_params Set SCF Convergence Parameters (Optional) dm21_assign->scf_params scf_calc Perform Self-Consistent Field (SCF) Calculation scf_params->scf_calc nn_eval This compound Neural Network Evaluates E_xc scf_calc->nn_eval During SCF cycles energy_out Output: Total Energy scf_calc->energy_out nn_eval->scf_calc geom_opt Geometry Optimization? energy_out->geom_opt num_grad Calculate Numerical Nuclear Gradients geom_opt->num_grad Yes end End geom_opt->end No opt_step Optimizer Updates Geometry num_grad->opt_step conv_check Converged? opt_step->conv_check conv_check->scf_calc No conv_check->end Yes

Caption: Workflow for this compound molecular energy and geometry optimization calculations.

Decision Logic for Functional Selection

Choosing the appropriate density functional is a critical step in computational chemistry. This diagram provides a simplified decision-making process for when to consider using this compound.

start Start: New Computational Chemistry Task problem_type What is the primary computational goal? start->problem_type energy_calc High-accuracy single-point energy calculation problem_type->energy_calc Energy geom_opt Routine geometry optimization problem_type->geom_opt Geometry system_type Does the system involve fractional electron character? (e.g., bond stretching, charge transfer) energy_calc->system_type use_traditional Use traditional functionals (e.g., B3LYP, PBE0, ωB97X-V) with analytical gradients geom_opt->use_traditional use_this compound Consider this compound for higher accuracy system_type->use_this compound Yes is_transition_metal Does the system contain transition metals? system_type->is_transition_metal No is_transition_metal->use_this compound No caution_this compound Use this compound with caution (potential convergence issues) is_transition_metal->caution_this compound Yes caution_this compound->use_traditional If convergence fails

Caption: Decision tree for selecting this compound versus traditional DFT functionals.

This compound's Approach to Fractional Electron Error

This diagram illustrates the conceptual difference between how traditional DFAs and this compound handle systems with fractional electron character, a key source of delocalization error.

cluster_0 Traditional DFA cluster_1 This compound a1 System with Fractional Electron Character a2 DFA favors delocalized electron density a1->a2 a3 Incorrect energy prediction (Delocalization Error) a2->a3 b1 System with Fractional Electron Character b2 Training on systems with fractional charges and spins b1->b2 b3 Neural network learns to correctly localize electron density b2->b3 b4 Accurate energy prediction b3->b4

Caption: Conceptual comparison of traditional DFAs and this compound for fractional electron systems.

Troubleshooting and Best Practices

  • SCF Convergence: For calculations that struggle to converge, consider the following strategies in PySCF:

    • DIIS Space: Increase the Direct Inversion in the Iterative Subspace (DIIS) space (mf.diis_space).

    • Level Shifting: Apply a level shift to aid convergence in systems with small HOMO-LUMO gaps (mf.level_shift).[9]

    • Damping: Damp the Fock matrix in the initial SCF cycles (mf.damp).[6][9]

    • Initial Guess: Use a converged density matrix from a calculation with a smaller basis set or a more stable functional as the initial guess.

  • Geometry Optimization:

    • Convergence Criteria: It may be necessary to use tighter convergence criteria for the SCF cycles within each optimization step to mitigate the effects of numerical noise.

    • Optimizer Choice: The Berny optimizer is a common choice in PySCF. For particularly challenging optimizations, exploring other optimizers or adjusting their parameters may be beneficial.

  • Applicability:

    • Main Group Chemistry: this compound has shown excellent performance for main group elements.

    • Transition Metals: Exercise caution when applying this compound to systems containing transition metals, as convergence issues are more likely.[7] It is recommended to first benchmark against known results for similar systems.

References

Application Notes and Protocols for DM21 Functional in PySCF for Geometry Optimization

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction

The DeepMind21 (DM21) functional is a neural network-based exchange-correlation functional that has shown promise in delivering high accuracy for electronic energy calculations, particularly for systems with strong correlation and charge delocalization.[1][2] Developed by Google DeepMind, this compound is available as an extension to the PySCF quantum chemistry software package.[2][3] These application notes provide a detailed guide for utilizing the this compound functional for molecular geometry optimization within PySCF, including protocols, performance considerations, and comparisons with traditional functionals.

While this compound has demonstrated significant accuracy in energy calculations, its application to geometry optimization presents unique challenges and considerations.[1][4] Research indicates that numerical noise from the neural network can affect the smoothness of the potential energy surface and the accuracy of nuclear gradients, which are crucial for efficient geometry optimization.[4][5][6] Despite these challenges, with appropriate settings, this compound can be a valuable tool for obtaining optimized molecular geometries.

Key Features and Considerations of this compound for Geometry Optimization

  • Potential for High Accuracy: For certain systems, this compound has the potential to yield highly accurate geometries, competitive with or even exceeding traditional functionals.[1]

  • Numerical Noise: The neural network architecture of this compound can introduce numerical noise, which may contaminate the nuclear gradients required for geometry optimization.[4][5][6] This can lead to less smooth potential energy surfaces and potentially affect the convergence and precision of the optimization.[5]

  • Computational Cost: Geometry optimizations using this compound are significantly slower and more computationally expensive compared to analytical functionals.[5][7] This is a critical factor to consider for large-scale screening or studies involving large molecules.

  • SCF Convergence: Achieving self-consistent field (SCF) convergence with this compound can be more challenging than with traditional functionals, particularly for complex systems like those containing transition metals.[7]

Experimental Protocols

This section details the protocol for performing a geometry optimization using the this compound functional in PySCF.

Installation and Setup

Ensure that PySCF and the this compound extension are properly installed. The this compound functional can be installed as a Python package.

Defining the Molecule

First, define the molecular system using PySCF's gto.Mole class.

Setting up the this compound Calculation

To use the this compound functional, you need to import it and assign it to the xc attribute of a scf.RKS or scf.UKS object.

Performing the Geometry Optimization

PySCF's geomopt module can be used to perform the geometry optimization. The optimize function takes the SCF object as input. It is crucial to use numerical gradients for this compound. Recent studies have shown that a numerical differentiation step in the range of 0.0001-0.001 Å is required to obtain sufficiently smooth nuclear gradients.[4][5]

Advanced Convergence Settings

For challenging optimizations, it may be necessary to adjust the convergence parameters for the geometry optimizer. PySCF's interface to the geomeTRIC library allows for fine-tuning of these settings.[8]

Caption: Workflow for this compound geometry optimization in PySCF.

G cluster_performance Performance Comparison of Functionals for Geometry Optimization This compound This compound Pros: - Potentially high accuracy for specific systems - Handles strong correlation Cons: - High computational cost - Numerical noise in gradients - SCF convergence issues Traditional Traditional Functionals (PBE0, SCAN) Pros: - Faster computation - Smooth analytical gradients - Generally robust convergence Cons: - May struggle with strongly correlated systems This compound->Traditional Accuracy is competitive but not always superior

Caption: this compound vs. traditional functional performance.

References

Application Notes and Protocols: Investigating the Interaction of DM21 with Charged DNA Base Pairs

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

DNA, the blueprint of life, is a highly charged polyelectrolyte due to its phosphate backbone.[1][2] This inherent charge plays a crucial role in its structure, stability, and interaction with various molecules. Beyond the canonical Watson-Crick base pairing, DNA can adopt alternative secondary structures, such as G-quadruplexes, which are stabilized by the presence of cations and are particularly prevalent in telomeric regions and gene promoters. These non-canonical structures, with their unique charge distributions and topologies, represent novel targets for therapeutic intervention.

DM21 is a novel investigational compound that has demonstrated high affinity and specificity for G-quadruplex structures. Its proposed mechanism of action involves the selective recognition and stabilization of these four-stranded DNA conformations, leading to the modulation of downstream cellular processes. These application notes provide a comprehensive overview of the experimental protocols to characterize the interaction of this compound with charged DNA base pairs, specifically within the context of G-quadruplexes.

Hypothetical Signaling Pathway of this compound Action

The proposed mechanism of this compound involves its interaction with G-quadruplexes in the promoter regions of specific oncogenes, leading to the suppression of their transcription. This stabilization of the G-quadruplex structure is hypothesized to block the binding of transcription factors necessary for gene expression.

DM21_Signaling_Pathway cluster_cell Cancer Cell This compound This compound G4 G-Quadruplex (Promoter Region) This compound->G4 Binds & Stabilizes TF Transcription Factors G4->TF Blocks Binding Oncogene Oncogene (e.g., c-MYC) TF->Oncogene Activates mRNA mRNA Transcription Oncogene->mRNA Transcription Protein Oncogenic Protein mRNA->Protein Translation Proliferation Tumor Growth & Proliferation Protein->Proliferation Promotes caption Proposed signaling pathway of this compound.

Caption: Proposed signaling pathway of this compound.

Experimental Protocols

Detailed methodologies for key experiments to characterize the interaction of this compound with G-quadruplex DNA are provided below.

G-Quadruplex Formation and Verification

Objective: To form stable G-quadruplex structures from synthetic oligonucleotides and verify their conformation.

Materials:

  • Synthetic G-rich oligonucleotide (e.g., from the promoter region of c-MYC: 5'-TGAGGGTGGGTAGGGTGGGTAA-3')

  • Annealing Buffer: 10 mM Tris-HCl (pH 7.5), 100 mM KCl

  • Nuclease-free water

  • Circular Dichroism (CD) Spectropolarimeter

Protocol:

  • Resuspend the synthetic oligonucleotide in nuclease-free water to a stock concentration of 1 mM.

  • Dilute the oligonucleotide to a final concentration of 100 µM in the annealing buffer.

  • Heat the solution to 95°C for 5 minutes.

  • Allow the solution to slowly cool to room temperature over several hours to facilitate G-quadruplex formation.

  • Verify the formation of the G-quadruplex structure using Circular Dichroism (CD) spectroscopy. A characteristic CD spectrum with a positive peak around 264 nm and a negative peak around 240 nm indicates the formation of a parallel G-quadruplex.

Characterization of this compound-G-Quadruplex Binding

Objective: To determine the binding affinity and stoichiometry of this compound to the pre-formed G-quadruplex DNA.

Methods:

  • UV-Vis Spectroscopy: To observe changes in the absorbance spectrum of this compound upon binding to the G-quadruplex.

  • Fluorescence Spectroscopy: To monitor changes in the fluorescence emission of this compound or a fluorescently labeled G-quadruplex upon binding.

  • Isothermal Titration Calorimetry (ITC): To directly measure the thermodynamic parameters of binding.

2.1 UV-Vis Titration Protocol:

  • Prepare a solution of 10 µM pre-formed G-quadruplex DNA in the annealing buffer.

  • Prepare a stock solution of 1 mM this compound in a compatible solvent (e.g., DMSO) and then dilute to 100 µM in the annealing buffer.

  • Place the G-quadruplex solution in a quartz cuvette and record the initial UV-Vis spectrum (200-600 nm).

  • Titrate small aliquots (1-5 µL) of the this compound solution into the cuvette.

  • After each addition, mix thoroughly and record the UV-Vis spectrum.

  • Continue the titration until no further significant changes in the spectrum are observed.

  • Analyze the data to determine the binding constant (Kb).

2.2 Fluorescence Titration Protocol:

  • Prepare a solution of 1 µM pre-formed G-quadruplex DNA in the annealing buffer.

  • Prepare a stock solution of this compound as described above.

  • Excite the sample at the appropriate wavelength for this compound and record the emission spectrum.

  • Perform a titration by adding increasing concentrations of the G-quadruplex DNA to the this compound solution.

  • Record the fluorescence spectrum after each addition.

  • Plot the change in fluorescence intensity as a function of the G-quadruplex concentration to determine the binding affinity.

2.3 Isothermal Titration Calorimetry (ITC) Protocol:

  • Prepare a 10 µM solution of the G-quadruplex and a 100 µM solution of this compound in the same buffer.

  • Degas both solutions to remove any dissolved air bubbles.

  • Load the G-quadruplex solution into the sample cell of the ITC instrument and the this compound solution into the injection syringe.

  • Set the experimental parameters (temperature, injection volume, spacing between injections).

  • Perform the titration experiment, injecting the this compound solution into the G-quadruplex solution.

  • Analyze the resulting thermogram to determine the binding affinity (Ka), enthalpy (ΔH), and stoichiometry (n) of the interaction.

G-Quadruplex Stabilization Assay

Objective: To assess the ability of this compound to stabilize the G-quadruplex structure.

Method:

  • Fluorescence Resonance Energy Transfer (FRET) Melting Assay: This assay uses a dually labeled oligonucleotide with a fluorophore and a quencher. In the G-quadruplex conformation, the fluorophore and quencher are in close proximity, resulting in low fluorescence. Upon melting, the structure unfolds, separating the fluorophore and quencher, leading to an increase in fluorescence.

Protocol:

  • Use a synthetic oligonucleotide labeled with a FRET pair (e.g., FAM as the fluorophore and TAMRA as the quencher).

  • Form the G-quadruplex as described in Protocol 1.

  • Prepare a series of solutions containing the labeled G-quadruplex (100 nM) and varying concentrations of this compound (e.g., 0-10 µM).

  • Use a real-time PCR machine or a fluorometer with temperature control to monitor the fluorescence as the temperature is increased from 25°C to 95°C in increments of 1°C/minute.

  • The melting temperature (Tm) is the temperature at which 50% of the G-quadruplexes are unfolded.

  • Plot the Tm as a function of this compound concentration. An increase in Tm indicates stabilization of the G-quadruplex by this compound.

Experimental Workflow

The following diagram illustrates the overall workflow for investigating the interaction of this compound with G-quadruplex DNA.

Experimental_Workflow cluster_prep Preparation cluster_binding Binding Characterization cluster_stabilization Stabilization Assay Oligo Synthetic G-rich Oligonucleotide Anneal Annealing to form G-Quadruplex Oligo->Anneal Verify CD Spectroscopy Verification Anneal->Verify UVVis UV-Vis Titration Verify->UVVis Fluorescence Fluorescence Titration Verify->Fluorescence ITC Isothermal Titration Calorimetry Verify->ITC FRET FRET Melting Assay Verify->FRET Data_Analysis Data Analysis & Interpretation UVVis->Data_Analysis Determine Kb Fluorescence->Data_Analysis Determine Kd ITC->Data_Analysis Determine Ka, ΔH, n FRET->Data_Analysis Determine ΔTm caption Experimental workflow for this compound analysis.

Caption: Experimental workflow for this compound analysis.

Data Presentation

The quantitative data obtained from the described experiments should be summarized in clear and concise tables for easy comparison and interpretation.

Table 1: Binding Parameters of this compound to G-Quadruplex DNA

MethodParameterValue (Hypothetical)Units
UV-Vis SpectroscopyBinding Constant (Kb)1.5 x 106M-1
Fluorescence SpectroscopyDissociation Constant (Kd)0.67µM
Isothermal Titration CalorimetryAssociation Constant (Ka)1.8 x 106M-1
Enthalpy (ΔH)-12.5kcal/mol
Stoichiometry (n)2:1 (this compound:G4)-

Table 2: G-Quadruplex Stabilization by this compound (FRET Melting Assay)

This compound Concentration (µM)Melting Temperature (Tm) (°C)ΔTm (°C)
0 (Control)62.50.0
0.565.83.3
1.068.25.7
2.572.19.6
5.075.412.9
10.078.015.5

Conclusion

These application notes provide a foundational framework for researchers to investigate the interaction of the novel compound this compound with charged DNA base pairs, specifically within G-quadruplex structures. The detailed protocols and data presentation guidelines will enable a thorough characterization of the binding affinity, thermodynamics, and stabilizing effects of this compound, providing crucial insights for its further development as a potential therapeutic agent. The experimental approaches described are also broadly applicable to the study of other small molecule interactions with non-canonical DNA structures.

References

Application Note: Modeling Diradical Transition States with the DM21 Functional

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction: The Challenge of Diradical Transition States

Diradical species, molecules with two unpaired electrons, are critical intermediates and transition states in a vast array of chemical reactions, including pericyclic reactions, bond homolysis, and certain catalytic cycles.[1] A transition state with significant diradical character possesses a multiconfigurational electronic structure, meaning that a single determinant method like standard Kohn-Sham Density Functional Theory (KS-DFT) is often inadequate for an accurate description.[2] Traditional DFT functionals frequently suffer from "pathological errors" in such systems, notably delocalization error and artificial spin symmetry breaking, which can lead to qualitatively incorrect reaction barriers and mechanistic predictions.[1]

The DM21 Functional: A Potential Solution

This compound is a machine-learned exchange-correlation functional developed by DeepMind.[3][4] Unlike traditional functionals, it was specifically trained to handle systems with "fractional electron character," including fractional charges and spins.[1][3] This training methodology was designed to explicitly correct the systemic flaws of delocalization and spin symmetry-breaking.[1] By generating an accurate dissociation limit for molecules like H₂ without breaking spin symmetry, this compound demonstrates a theoretical aptitude for describing the bond-stretching and bond-breaking processes inherent to the formation of diradical transition states.[5]

However, the practical application of this compound comes with significant challenges, including severe Self-Consistent Field (SCF) convergence difficulties and high computational cost.[6][7] This note provides a detailed protocol for attempting to model diradical transition states with this compound, along with a realistic assessment of its current limitations.

Performance and Data

While direct benchmark data for this compound on a wide range of diradical transition states is not yet prevalent in the literature, its performance on related problems, such as bond dissociation, is indicative of its potential. The Bond-Breaking Benchmark (BBB) provides a relevant assessment.

Table 1: Mean Absolute Errors (kcal/mol) on the Bond-Breaking Benchmark (BBB)
FunctionalTypeMean Absolute Error (kcal/mol)
This compound Machine-Learned Hybrid< 5.0 (Reported Superiority) [3][5]
SCAN meta-GGA~5-10
wB97X Range-Separated Hybrid~5-10
B3LYP Hybrid-GGA>10

Data is synthesized from performance charts and statements in cited literature comparing this compound to high-performing functionals on the BBB dataset.[3][5]

Table 2: Qualitative Feature Comparison for Diradical Modeling
FeatureThis compoundStandard Hybrids (e.g., B3LYP)Multireference (e.g., CASSCF)
Static Correlation Partially captured via FS trainingPoorly describedExplicitly included
Spin Contamination Designed to minimizeOften significant (UHF/UKS)Well-defined spin states
Delocalization Error Significantly reducedHighN/A
Computational Cost Very High (per iteration)[6]Low to ModerateExtremely High
Ease of Use Difficult (Convergence)[6]RoutineRequires expert knowledge
Analytical Gradients Not available[7][8]AvailableAvailable

Decision Workflow for Using this compound

Before attempting a calculation, researchers should consider if this compound is the appropriate tool. The following workflow helps guide this decision.

start Start: System with potential diradical transition state q1 Is the system a main-group organic or organometallic species? start->q1 q2 Are significant computational resources available? q1->q2 Yes no_tm This compound has severe convergence issues with transition metals. Proceed with extreme caution or use alternative methods. q1->no_tm No (Transition Metal) q3 Have standard methods (e.g., B3LYP-D3) provided questionable results? q2->q3 Yes alt_method Consider alternative methods: - Broken-Symmetry DFT - Multireference (CASSCF, NEVPT2) - EOM-SF-CCSD q2->alt_method No use_this compound Proceed with this compound Protocol (High-risk, high-reward) q3->use_this compound Yes q3->alt_method No no_tm->alt_method

Caption: Decision workflow for selecting this compound for diradical modeling.

Computational Protocol for Diradical Transition State Modeling

This protocol is designed for the PySCF computational chemistry package, where this compound is readily available.[4][9]

Part 1: Initial Structure and Broken-Symmetry Guess

A good initial guess for both the geometry and the electronic structure is critical.

  • Construct an initial guess geometry for the transition state using chemical intuition, manual building, or results from a lower-level scan.

  • Perform a preliminary geometry optimization and frequency calculation using a standard, robust functional like B3LYP with an unrestricted formalism (UKS). Use the guess(mix=True) option in PySCF to encourage spin-symmetry breaking, which can help locate an initial diradical-like solution.

  • Verify the B3LYP result: Ensure the optimized structure has one imaginary frequency corresponding to the desired reaction coordinate. Save the optimized geometry and the final orbitals/density matrix.

Part 2: this compound Self-Consistent Field (SCF) Calculation

This compound is known to have severe convergence issues.[6] A multi-stage strategy is recommended. The orbitals from the B3LYP calculation should be used as the initial guess.

  • Strategy A (Standard): Start with moderate level shifting and damping.

    • level_shift = 0.25

    • damp = 0.7

    • Set a high number of maximum SCF cycles (max_cycle = 200).[6]

  • Strategy B (Aggressive Damping): If Strategy A fails, increase damping and the number of cycles.

    • damp = 1.0

    • max_cycle = 500[6]

  • Strategy C (DIIS Delay): If Strategy B fails, delay the start of the DIIS (Direct Inversion in the Iterative Subspace) procedure.

    • diis_start_cycle = 12 (or higher)

    • max_cycle = 900[6]

  • Non-Self-Consistent Check: If all SCF strategies fail, consider a non-self-consistent calculation (this compound@B3LYP). This involves running a single this compound energy evaluation on the converged B3LYP orbitals. Studies have shown this can yield improved accuracy over self-consistent B3LYP, though it is not a true this compound result.[6]

Part 3: Transition State Optimization with this compound

This compound lacks analytical gradients, so optimization must proceed with numerical differentiation, which can be noisy.[5][8]

  • Optimizer Setup: Use the geometry from the successful Part 1 calculation as the starting point.

  • Initial Hessian: It is highly recommended to compute the Hessian matrix at the starting geometry using the this compound functional to provide the optimizer with accurate initial curvature information.

  • Numerical Differentiation Step: A numerical differentiation step in the range of 0.0001–0.001 Å has been found to be required for sufficiently smooth gradients.[5][8] This may need to be adjusted in the optimizer settings.

  • Convergence Criteria: Begin with loose optimization criteria. Once the optimization converges, use the resulting structure as the input for a subsequent optimization with tighter criteria.

  • Execution: Run the transition state optimization using a robust algorithm like the Berny optimizer. Be prepared for a large number of optimization cycles.

Part 4: Verification

  • Frequency Calculation: Upon successful convergence of the geometry, perform a numerical frequency calculation at the this compound level.

  • Analysis: A true transition state will have exactly one imaginary frequency. Animate this vibrational mode to confirm that it corresponds to the expected reaction coordinate. If there are zero or multiple imaginary frequencies, the located structure is not the correct transition state.

Workflow Visualization

The following diagram illustrates the key steps of the computational protocol.

start 1. Initial TS Guess (Geometry) bs_opt 2. Broken-Symmetry Opt+Freq (e.g., UKS-B3LYP) - Use guess(mix=True) - Obtain orbitals & geometry start->bs_opt dm21_scf 3. This compound SCF Calculation (Using B3LYP orbitals) bs_opt->dm21_scf scf_strat_a Strategy A (level_shift, damp) dm21_scf->scf_strat_a scf_strat_b Strategy B (more damp) scf_strat_a->scf_strat_b scf_strat_c Strategy C (delay DIIS) scf_strat_b->scf_strat_c ts_opt 4. This compound TS Optimization - Use numerical gradients - Calculate initial Hessian - Start with loose criteria scf_strat_c->ts_opt Converged fail SCF or Opt Failed: - Re-evaluate initial guess - Consider this compound@B3LYP - Use alternative method scf_strat_c->fail Failed verify 5. This compound Numerical Frequency Calculation ts_opt->verify Converged ts_opt->fail Failed end Result: Verified Diradical Transition State verify->end One Imaginary Freq verify->fail 0 or >1 Imaginary Freq

Caption: Computational workflow for this compound diradical transition state modeling.

Summary and Outlook

The this compound functional is a promising, theoretically-grounded tool for investigating reactions involving diradical character due to its design which mitigates common DFT errors. However, its practical application is currently hampered by severe computational challenges, including poor SCF convergence and the lack of analytical gradients for geometry optimization. The protocols outlined in this note provide a roadmap for expert users to attempt these demanding calculations. As the implementation of machine-learned functionals becomes more efficient and robust, this compound and its successors may evolve into indispensable tools for accurately modeling complex, open-shell chemical reactivity.

References

DM21: Application Notes and Protocols for Studying Noncovalent Interactions

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

DM21, a deep learning-based density functional, represents a significant advancement in the accurate computation of electronic structure.[1][2] Developed by DeepMind, this neural network functional is designed to approximate the exchange-correlation energy in Density Functional Theory (DFT), overcoming some of the systemic errors found in traditional functionals, particularly in systems with fractional electron character.[1][2][3] Its demonstrated high accuracy on benchmark datasets like GMTKN55 makes it a promising tool for studying noncovalent interactions, which are critical in fields ranging from materials science to drug discovery.[1][3]

These application notes provide an overview of this compound's performance, protocols for its use in studying noncovalent interactions via the PySCF software package, and visualizations to aid in understanding its application.

Performance of this compound for Noncovalent Interactions

This compound has shown competitive performance against a range of established DFT functionals in the GMTKN55 benchmark, a comprehensive database for general main group thermochemistry, kinetics, and noncovalent interactions.[1][3] The following table summarizes the mean absolute error (MAE) of this compound in comparison to other functionals on the GMTKN55 benchmark.

FunctionalMean Absolute Error (kcal/mol) on GMTKN55
This compound 1.5 [1]
SCAN3.6[1]
revPBE:D3(BJ)Competitive with this compound[3]
PW6B95:D3(0)Competitive with this compound[3]
DSD-PBEP86:D3(BJ) (Double Hybrid)Outperforms this compound[3]

Note: Lower MAE values indicate higher accuracy. The D3 dispersion correction is often used with traditional functionals to improve their description of noncovalent interactions.

Experimental Protocols

The following protocols outline the general steps for utilizing this compound to study noncovalent interactions using the PySCF quantum chemistry software package.

Protocol 1: Single-Point Energy Calculation of a Noncovalent Complex

This protocol describes how to calculate the interaction energy of a molecular complex bound by noncovalent forces.

1. Installation and Setup:

  • Ensure PySCF is installed.

  • Install the this compound extension for PySCF from the official DeepMind GitHub repository.

2. Define the Molecular Geometry:

  • Create a Python script.

  • Import the necessary libraries from PySCF and the this compound extension.

  • Define the molecular geometry of the entire complex in Cartesian coordinates. The geometry can be read from a file (e.g., XYZ or MOL file) or defined directly in the script.

3. Perform the DFT Calculation for the Complex:

  • Create a molecule object in PySCF using the defined geometry.

  • Set up the DFT calculation object, specifying the this compound functional.

  • Run the self-consistent field (SCF) calculation to obtain the total energy of the complex.

4. Perform DFT Calculations for Monomers:

  • Repeat step 3 for each individual monomer of the complex, using the same atomic coordinates as in the complex to avoid geometry-related errors (this is known as the counterpoise correction basis set superposition error mitigation strategy).

5. Calculate the Interaction Energy:

  • The interaction energy (IE) is calculated as:

    • IE = E_complex - (E_monomer1 + E_monomer2 + ...)

Example Python (PySCF) Snippet:

Protocol 2: Geometry Optimization of a Noncovalent Complex

This protocol is for finding the minimum energy structure of a noncovalent complex.

1. Installation and Setup:

  • As in Protocol 1.

2. Define the Initial Molecular Geometry:

  • Define an initial guess for the geometry of the complex. The accuracy of the initial guess can affect the convergence of the optimization.

3. Perform the Geometry Optimization:

  • Create a molecule object and a DFT calculation object as in Protocol 1.

  • Use the optimizer function from PySCF to perform the geometry optimization. This will iteratively update the geometry to find the structure with the lowest energy.

4. Analyze the Optimized Geometry:

  • The optimized geometry provides insights into the preferred orientation and intermolecular distances of the noncovalent complex.

Visualizations

This compound in the DFT Landscape

The following diagram illustrates the position of this compound within the hierarchy of Density Functional Theory methods.

dft Density Functional Theory (DFT) lda Local Density Approximation (LDA) dft->lda gga Generalized Gradient Approximation (GGA) lda->gga mgga Meta-GGA gga->mgga hybrid Hybrid Functionals mgga->hybrid ml Machine-Learned Functionals hybrid->ml This compound This compound ml->this compound

Caption: Hierarchy of DFT functionals, with this compound as a machine-learned functional.

Workflow for a this compound Calculation

This diagram outlines the typical computational workflow for a noncovalent interaction study using this compound.

start Define Molecular System (Geometry, Basis Set) setup Set up PySCF Calculation (Specify this compound functional) start->setup scf Self-Consistent Field (SCF) Calculation setup->scf converged SCF Converged? scf->converged converged->scf No (Adjust SCF parameters) energy Calculate Total Energy converged->energy Yes analysis Analyze Results (e.g., Interaction Energy) energy->analysis stop End analysis->stop

Caption: Computational workflow for a this compound calculation in PySCF.

Considerations and Limitations

  • SCF Convergence: While powerful, this compound can sometimes present challenges in achieving self-consistent field (SCF) convergence, particularly for systems containing transition metals.[4] Users may need to employ advanced SCF convergence algorithms available in PySCF.

  • Computational Cost: As a neural network-based functional, this compound calculations may be more computationally demanding than traditional functionals.

  • Availability: this compound is available as an extension to the PySCF programming framework.[1]

Conclusion

This compound offers a highly accurate and promising approach for the computational study of noncovalent interactions. Its ability to overcome some of the inherent limitations of traditional DFT functionals makes it a valuable tool for researchers in chemistry, materials science, and drug development. By following the outlined protocols, researchers can leverage the power of this compound to gain deeper insights into the nature and strength of noncovalent bonds in their systems of interest.

References

Application Notes and Protocols for DM21 in Main Group Thermochemistry

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

These application notes provide a comprehensive guide to setting up and utilizing the DM21 density functional for main group thermochemistry studies. The notes include an overview of the functional, performance benchmarks, detailed computational protocols, and a visual workflow to ensure successful implementation in your research.

Introduction to this compound

The DeepMind 21 (this compound) is a state-of-the-art machine-learned density functional approximation (DFA) that has demonstrated high accuracy for main group thermochemistry.[1] Developed through deep learning, this compound was trained on fractional charge and fractional spin systems to overcome some of the inherent limitations of traditional DFAs.[2] This has resulted in a functional that shows performance comparable or even superior to established methods like B3LYP for a range of main group chemical systems. However, users should be aware that self-consistent field (SCF) convergence can be a challenge with this compound, often requiring specific computational strategies to overcome.

Data Presentation: Performance Benchmarks

This compound has been rigorously tested on various benchmark datasets for main group thermochemistry. A key benchmark is the General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) database. The performance of this compound in comparison to other well-established functionals is summarized below.

FunctionalBenchmarkMean Absolute Error (MAE) (kcal/mol)
This compound GMTKN55 1.5 [1]
SCANGMTKN553.6[1]
B3LYP-Comparable or lower accuracy than this compound for main group thermochemistry.

Note: The lower MAE for this compound on the comprehensive GMTKN55 benchmark indicates its high potential for accurate thermochemical predictions in main group chemistry.

Experimental Protocols: Computational Thermochemistry with this compound

This section outlines the detailed protocols for performing thermochemical studies on main group molecules using the this compound functional within the PySCF quantum chemistry software package.[3]

Protocol 1: Geometry Optimization

A crucial first step in any thermochemistry study is to obtain the optimized equilibrium geometry of the molecule.

Objective: To find the minimum energy structure of the molecule of interest using the this compound functional.

Software: PySCF

Procedure:

  • Molecule Definition: Define the molecular geometry in PySCF using standard methods (e.g., by providing Cartesian coordinates).

  • SCF Calculation Setup:

    • Specify the use of the this compound functional. This is typically done by interfacing with the density_functional_approximation_this compound library.

    • Define the basis set (e.g., 'cc-pVTZ').

    • Set up the SCF calculation object.

  • Addressing SCF Convergence:

    • Due to the nature of the machine-learned functional, SCF convergence can be challenging. It is highly recommended to implement the following strategies from the outset:

      • Level Shifting: Apply a level shift to the virtual orbitals to aid convergence. A starting value of 0.5 Hartrees is recommended.

      • Damping: Introduce damping to the SCF iterations to prevent large oscillations. A damping factor of 0.5 is a good starting point.

    • It is also beneficial to start the DIIS (Direct Inversion in the Iterative Subspace) procedure after a few initial cycles (e.g., start DIIS at cycle 2).

  • Geometry Optimization:

    • Use the SCF object with the specified convergence parameters to perform the geometry optimization.

    • The optimization will iteratively update the nuclear coordinates until a stationary point on the potential energy surface is found.

  • Verification:

    • After the optimization, verify that the calculation has converged to a true minimum by performing a frequency calculation (see Protocol 2). The absence of imaginary frequencies confirms a minimum energy structure.

Protocol 2: Thermochemical Property Calculation

Once the geometry is optimized, a frequency calculation is performed to obtain key thermochemical data.

Objective: To calculate the vibrational frequencies and derive thermochemical properties such as enthalpy and Gibbs free energy.

Software: PySCF

Procedure:

  • Optimized Geometry: Use the optimized molecular geometry obtained from Protocol 1.

  • Frequency Calculation:

    • Set up a frequency analysis calculation using the this compound functional and the same basis set as in the geometry optimization.

    • This calculation will compute the second derivatives of the energy with respect to the nuclear coordinates.

  • Thermochemical Analysis:

    • The output of the frequency calculation will provide the vibrational frequencies.

    • Use these frequencies to compute the zero-point vibrational energy (ZPVE), thermal corrections to the enthalpy, and the entropy.

    • The total enthalpy (H) and Gibbs free energy (G) can then be calculated by adding these thermal corrections to the electronic energy obtained from the optimized geometry.

  • Data Extraction:

    • Extract the calculated thermochemical properties for further analysis, such as determining reaction enthalpies and free energies.

Mandatory Visualization

Computational Workflow for Main Group Thermochemistry Studies using this compound

The following diagram illustrates the logical workflow for conducting a thermochemical study with the this compound functional.

DM21_Thermochemistry_Workflow cluster_prep 1. Preparation cluster_geom_opt 2. Geometry Optimization cluster_thermo 3. Thermochemistry cluster_analysis 4. Analysis mol_def Define Molecule (Coordinates, Charge, Spin) scf_setup Setup this compound SCF - Basis Set - Convergence Aids (Level Shift, Damp) mol_def->scf_setup geom_opt Run Geometry Optimization scf_setup->geom_opt freq_check Frequency Check (Confirm Minimum) geom_opt->freq_check freq_calc Perform Frequency Calculation freq_check->freq_calc No Imaginary Frequencies thermo_props Calculate Thermochemical Properties (H, G, S) freq_calc->thermo_props data_analysis Analyze Thermochemical Data (e.g., Reaction Enthalpies) thermo_props->data_analysis

Caption: Workflow for this compound thermochemistry calculations.

References

Practical Guide to DM21 Functional Implementation for Drug Development

Author: BenchChem Technical Support Team. Date: November 2025

Application Notes and Protocols for Researchers, Scientists, and Drug Development Professionals

This document provides a comprehensive guide to the functional implementation of DM21, a next-generation maytansinoid payload for antibody-drug conjugates (ADCs). The information is intended for researchers, scientists, and drug development professionals engaged in the preclinical evaluation of ADCs.

Introduction to this compound

This compound is a potent maytansinoid payload designed for use in ADCs. It is a microtubule-disrupting agent that induces cell cycle arrest and apoptosis in targeted cancer cells. A key feature of this compound is its peptide-cleavable linker, which allows for the efficient release of a hydrophobic, membrane-permeable metabolite. This property facilitates a significant "bystander effect," enabling the killing of adjacent, antigen-negative tumor cells, which is particularly advantageous in treating heterogeneous tumors.[1][2]

One of the primary examples of a this compound-based ADC is IMGC936, which targets ADAM9, a cell surface protein overexpressed in various solid tumors.[3][4] Preclinical studies of IMGC936 have demonstrated potent anti-tumor activity and a favorable safety profile.[2][5]

Mechanism of Action

The functional implementation of a this compound-based ADC involves a multi-step process that begins with the binding of the ADC to its target antigen on the cancer cell surface and culminates in apoptosis of the target cell and surrounding bystander cells.

Signaling Pathway and Cellular Trafficking

The mechanism of action of a this compound-ADC, such as IMGC936, is initiated by the binding of the antibody component to its specific antigen on the tumor cell surface (e.g., ADAM9). This is followed by internalization of the ADC-antigen complex through receptor-mediated endocytosis. The complex is then trafficked to the lysosome, where the peptide linker is cleaved by proteases, releasing the active this compound metabolite, DM51, and its S-methylated catabolite, DM50.[3][5] These metabolites then bind to tubulin, disrupting microtubule dynamics, which leads to cell cycle arrest in the G2-M phase and subsequent apoptosis.[3]

DM21_Mechanism_of_Action cluster_extracellular Extracellular Space cluster_cell Cancer Cell cluster_cytoplasm Cytoplasm cluster_endosome Endosome/Lysosome cluster_bystander Bystander Cancer Cell ADC This compound-ADC Antigen Target Antigen (e.g., ADAM9) ADC->Antigen 1. Binding ADC_Internalized Internalized ADC-Antigen Complex Antigen->ADC_Internalized 2. Internalization Tubulin Tubulin Microtubule Microtubule Disruption Tubulin->Microtubule G2M G2/M Phase Cell Cycle Arrest Microtubule->G2M Apoptosis Apoptosis G2M->Apoptosis DM51_50 Active Metabolites (DM51, DM50) DM51_50->Tubulin 5. Target Engagement DM51_50_bystander Active Metabolites (DM51, DM50) DM51_50->DM51_50_bystander 6. Bystander Effect (Diffusion) Linker_Cleavage Proteolytic Linker Cleavage ADC_Internalized->Linker_Cleavage 3. Trafficking Linker_Cleavage->DM51_50 4. Payload Release Bystander_Apoptosis Apoptosis DM51_50_bystander->Bystander_Apoptosis

This compound-ADC Mechanism of Action

Data Presentation

The following tables summarize the quantitative data from preclinical studies of this compound-based ADCs.

Table 1: In Vitro Cytotoxicity of IMGC936 (this compound-ADC)
Cell LineCancer TypeTarget (ADAM9) ExpressionIC50 (nmol/L)
NCI-H1703Non-Small Cell LungPositive0.1 - 1.0
EBC-1Non-Small Cell LungPositive0.1 - 1.0
CAL-51Triple-Negative BreastPositive0.1 - 1.0
NCI-H1975Non-Small Cell LungPositive0.1 - 1.0

Note: Specific IC50 values are often proprietary. The range provided is based on the potent activity described in preclinical reports. The in vitro cytotoxicity of IMGC936 was found to be at least 2 logs greater than a non-targeting conjugate.[1]

Table 2: In Vivo Efficacy of a cMet-Targeting this compound-ADC in Xenograft Models[5]
Xenograft ModelCancer TypeTreatment Dose (mg/kg)Outcome
EBC-1Non-Small Cell Lung1.256/6 tumor-free survivors at day 49
Hs746TGastric2.58/8 tumor-free survivors at day 55
Table 3: Preclinical Toxicology of a Non-Targeting this compound-ADC (chKTI-DM21) in Cynomolgus Monkeys[2]
Dose Level (mg/kg)This compound Equivalent (µg/kg)Key Observations
11204Well-tolerated; transient increases in ALT and AST without histopathologic correlates.
22408Well-tolerated; transient increases in ALT and AST without histopathologic correlates.

Experimental Protocols

Detailed methodologies for key experiments in the functional implementation of this compound-ADCs are provided below.

Protocol 1: In Vitro Cytotoxicity Assay (MTT Assay)

This protocol is for determining the half-maximal inhibitory concentration (IC50) of a this compound-ADC on antigen-positive cancer cells.

Materials:

  • Antigen-positive (Ag+) and antigen-negative (Ag-) cell lines

  • Complete cell culture medium

  • This compound-ADC and a non-targeting control ADC

  • 96-well clear-bottom black plates

  • MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) solution (5 mg/mL in sterile PBS)

  • Solubilization solution (e.g., 10% SDS in 0.01 M HCl)

  • Microplate reader

Procedure:

  • Cell Seeding: Seed Ag+ and Ag- cells in separate 96-well plates at a density of 1,000-10,000 cells/well in 50 µL of complete medium. Incubate overnight at 37°C with 5% CO2.[6][7]

  • ADC Treatment: Prepare serial dilutions of the this compound-ADC and the non-targeting control ADC. Add 50 µL of the ADC solutions to the respective wells. Include untreated cells as a control.

  • Incubation: Incubate the plates for 48-144 hours at 37°C.[6]

  • MTT Addition: Add 20 µL of 5 mg/mL MTT solution to each well and incubate for 1-4 hours at 37°C.[6][7]

  • Solubilization: Add 100 µL of solubilization solution to each well and incubate overnight at 37°C in the dark.[7]

  • Data Acquisition: Read the absorbance at 570 nm using a microplate reader.

  • Data Analysis: Calculate the percentage of cell viability relative to untreated controls and determine the IC50 value using a suitable software.

Cytotoxicity_Workflow cluster_prep Preparation cluster_exp Experiment cluster_analysis Data Analysis Seed_Cells 1. Seed Ag+ and Ag- cells in 96-well plates Prepare_ADC 2. Prepare serial dilutions of this compound-ADC Add_ADC 3. Add ADC to cells and incubate (48-144h) Prepare_ADC->Add_ADC Add_MTT 4. Add MTT reagent and incubate (1-4h) Add_ADC->Add_MTT Add_Solubilization 5. Add solubilization buffer and incubate overnight Add_MTT->Add_Solubilization Read_Absorbance 6. Read absorbance at 570 nm Add_Solubilization->Read_Absorbance Calculate_IC50 7. Calculate % viability and determine IC50 Read_Absorbance->Calculate_IC50

In Vitro Cytotoxicity Assay Workflow
Protocol 2: Bystander Killing Co-culture Assay

This protocol evaluates the ability of a this compound-ADC to kill antigen-negative cells when co-cultured with antigen-positive cells.

Materials:

  • Antigen-positive (Ag+) cells

  • Antigen-negative (Ag-) cells stably expressing a fluorescent protein (e.g., GFP)

  • Complete cell culture medium

  • This compound-ADC

  • 96-well clear-bottom black plates

  • Fluorescence plate reader or flow cytometer

Procedure:

  • Cell Seeding: Seed a mixture of Ag+ and Ag--GFP cells in a 96-well plate. Vary the ratio of Ag+ to Ag--GFP cells (e.g., 90:10, 50:50, 10:90) while keeping the total cell number constant. Include wells with only Ag--GFP cells as a control.[6]

  • ADC Treatment: Add the this compound-ADC at a concentration that is highly cytotoxic to Ag+ cells but has low to no direct toxicity on Ag- cells (determined from the monoculture cytotoxicity assay).

  • Incubation: Incubate the plate for 48-144 hours at 37°C.[6]

  • Data Acquisition: Measure the GFP fluorescence in each well using a plate reader at different time points (e.g., 48, 96, 144 hours). Alternatively, harvest the cells and analyze the viability of the GFP-positive population by flow cytometry.[7]

  • Data Analysis: Normalize the fluorescence intensity of the treated co-culture wells to the untreated co-culture wells to determine the percent viability of the Ag--GFP cells. A decrease in viability of Ag--GFP cells in the presence of Ag+ cells indicates a bystander effect.

Bystander_Effect_Logic Ag_pos Antigen-Positive (Ag+) Cancer Cell Metabolite Released this compound Metabolite Ag_pos->Metabolite Internalizes & Releases Ag_neg Antigen-Negative (Ag-) Bystander Cell ADC This compound-ADC ADC->Ag_pos Targets ADC->Ag_neg Does NOT Target Metabolite->Ag_neg Diffuses to & Kills

Logical Relationship of the Bystander Effect
Protocol 3: this compound-Antibody Conjugation (Conceptual Workflow)

This protocol outlines the conceptual steps for the site-specific conjugation of the this compound payload to an antibody with engineered cysteine residues.

Materials:

  • Monoclonal antibody with engineered cysteine residues (e.g., at HC-C442)[3]

  • This compound-C linker-payload

  • Reducing agent (e.g., TCEP)

  • Reaction buffer (e.g., PBS)

  • Purification system (e.g., size-exclusion chromatography)

Procedure:

  • Antibody Reduction: Partially reduce the antibody to expose the engineered cysteine residues using a controlled amount of a reducing agent.

  • Conjugation Reaction: React the reduced antibody with the this compound-C linker-payload. The maleimide group on the linker will react with the free thiol of the cysteine residue.

  • Quenching: Quench any unreacted maleimide groups to prevent further reactions.

  • Purification: Purify the resulting ADC from unconjugated payload and other reactants using a suitable chromatography method.

  • Characterization: Characterize the purified ADC to determine the drug-to-antibody ratio (DAR), purity, and aggregation. A typical DAR for a site-specifically conjugated this compound-ADC is approximately 2.0.[3][5]

Conclusion

This compound is a promising maytansinoid payload for the development of next-generation ADCs. Its potent microtubule-disrupting activity, combined with a significant bystander effect, offers the potential for enhanced efficacy in treating solid tumors. The protocols and data presented in this guide provide a practical framework for the preclinical evaluation of this compound-based ADCs. Careful characterization of in vitro cytotoxicity, bystander killing, and in vivo efficacy, along with a thorough understanding of the mechanism of action, are critical for the successful translation of these promising therapeutics to the clinic.

References

Application Notes and Protocols for DM21 Calculations on Hydrogen Chain Systems

Application Notes and Protocols for the DM21 Functional Code

Author: BenchChem Technical Support Team. Date: November 2025

For Researchers, Scientists, and Drug Development Professionals

These notes provide detailed procedures for obtaining, installing, and utilizing the DM21 functional code, a machine-learned density functional approximation developed by DeepMind. This compound offers a novel approach to Density Functional Theory (DFT) calculations, aiming to overcome limitations of traditional functionals, particularly in systems with fractional electron character.[1]

Introduction to this compound

Quantitative Performance Data

This compound has been evaluated on several benchmark datasets and has shown state-of-the-art performance, outperforming many traditional functionals.[1] The following tables summarize the mean absolute errors (MAE) in kcal/mol for various benchmarks.

Table 1: Performance on General Benchmark Sets [4]

FunctionalBBB (MAE)GMTKN55 (MAE)QM9 (MAE)
This compound < 5 1.5 Not specified
SCANNot specified3.6Not specified
Best HybridNot specified> 1.5Not specified

Table 2: Performance on Transition Metal Chemistry (TMC117 Dataset) [5][6]

MethodMedian Absolute Error (kcal/mol)
B3LYP@B3LYP (self-consistent)3.0
This compound@B3LYP 2.3
This compound@this compound (self-consistent) 2.6

Note: "A@B" denotes an evaluation of functional A on the electron density computed by functional B.

Experimental Protocols

Obtaining the this compound Functional Code

The this compound functional code is available on the DeepMind research GitHub repository.

Protocol 1: Cloning the Repository

  • Prerequisite: Ensure you have Git installed on your system.

  • Open a terminal or command prompt.

  • Execute the following command to clone the repository:

  • The this compound code is located in the density_functional_approximation_this compound subdirectory.

Installation and Configuration

This compound is designed to be used with the PySCF quantum chemistry package.

Protocol 2: Setting up the Environment and Installation

  • Prerequisite: A working Python environment (e.g., Conda) is required.

  • Install PySCF: If not already installed, install PySCF using pip:

  • Install this compound dependencies: Navigate to the density_functional_approximation_this compound directory and install the required packages:

  • Add this compound to Python path: To make the this compound modules importable, add the density_functional_approximation_this compound directory to your PYTHONPATH environment variable. Alternatively, you can add the following to your Python script:

Running a Calculation with this compound

The following protocol outlines a basic self-consistent field (SCF) calculation on a methane molecule using this compound within PySCF.

Protocol 3: Example SCF Calculation

  • Create a Python script (e.g., run_this compound.py).

  • Import the necessary libraries from PySCF and this compound.

  • Define the molecule's geometry.

  • Initialize the this compound functional.

  • Run the SCF calculation.

Computational Workflow and Logical Relationships

The following diagrams illustrate the key workflows and relationships in using the this compound functional.

DM21_Installation_Workflow cluster_user User Actions cluster_system System State clone Clone DeepMind GitHub Repo repo Local Copy of This compound Code clone->repo install_pyscf Install PySCF pyscf PySCF Library install_pyscf->pyscf install_deps Install this compound Dependencies dm21_env This compound Environment install_deps->dm21_env set_path Set PYTHONPATH runnable Runnable this compound in Python set_path->runnable repo->install_deps dm21_env->set_path

Installation and setup workflow for the this compound functional.

DM21_Calculation_Workflow start Start: Define Molecule (Geometry, Basis Set) init_scf Initialize PySCF SCF Object start->init_scf patch_scf Patch SCF Object with this compound init_scf->patch_scf init_this compound Initialize this compound NeuralNumInt init_this compound->patch_scf run_scf Run SCF Calculation (mf.kernel()) patch_scf->run_scf get_energy Obtain Energy and other Properties run_scf->get_energy end End get_energy->end

Workflow for performing a quantum chemistry calculation with this compound.

Limitations and Considerations

While this compound shows great promise, researchers should be aware of its current limitations:

  • Computational Cost: this compound calculations are significantly more computationally expensive than traditional DFT functionals.[5] For instance, a single SCF iteration for n-decane can take several hours on multiple CPU cores.[5]

  • Transition Metal Chemistry: this compound can struggle with self-consistent field (SCF) convergence for transition metal-containing molecules, which may limit its practical applicability in this area.[5][6] However, evaluating the this compound functional on densities obtained from other functionals like B3LYP can still yield improved accuracy.[5][6]

  • Geometry Optimization: The numerical noise from the neural network can affect the calculation of nuclear gradients, which is crucial for geometry optimization.[7][8] This may require careful adjustment of numerical differentiation steps.[7][8] Studies have shown that for geometry optimization, this compound does not currently outperform analytical functionals in terms of accuracy and is slower.[7][9]

  • Periodic Systems: The current implementation has limitations for periodic systems and is primarily suited for molecular calculations.[10]

References

Application Notes and Protocols for Running DM21 in PySCF

Author: BenchChem Technical Support Team. Date: November 2025

Audience: Researchers, scientists, and drug development professionals.

This document provides detailed application notes and protocols for utilizing the DM21 density functional within the PySCF computational chemistry package. It includes example scripts for common calculations, a summary of performance benchmarks, and experimental protocols.

Introduction to this compound

The DeepMind 21 (this compound) functional is a machine-learned density functional that has shown promising accuracy for a variety of chemical systems.[1][2] It is available as an extension to the PySCF software package, allowing for its use in a range of quantum chemical calculations.[2] Unlike traditional density functionals, this compound is a neural network model that maps electron density to the exchange-correlation energy.[2] This approach has demonstrated state-of-the-art performance on several benchmark datasets, including GMTKN55 and QM9.[2][3]

Data Presentation

The performance of the this compound functional has been evaluated on various benchmark sets. Below is a summary of its Mean Absolute Error (MAE) compared to other common functionals on the LMGB35 benchmark.

BenchmarkBasis SetMetricThis compound MAEPBE0 MAESCAN MAE
LMGB35 6-31G(d,p)Bond Lengths (pm)0.8430.8030.795
LMGB35 def2-TZVPBond Lengths (pm)0.6250.9480.595
LMGB35 cc-pVQZEnergies (kcal/mol)2.1513.7573.978

Table 1: Mean Absolute Errors of this compound and other functionals on the LMGB35 benchmark.[1]

Experimental Protocols

This section provides detailed protocols for performing single-point energy calculations and geometry optimizations using the this compound functional in PySCF.

Installation and Setup

Before running this compound calculations, you need a working PySCF installation and the density_functional_approximation_this compound package.

Protocol 1: Installation

  • Install PySCF: Follow the official PySCF installation instructions. It is recommended to install it from source to ensure all dependencies are correctly handled.

  • Install the this compound library: The this compound functional is available as a separate Python package. Install it using pip:

Single-Point Energy Calculation

A single-point energy calculation computes the electronic energy of a molecule at a fixed geometry.

Protocol 2: Single-Point Energy Calculation with this compound

  • Import necessary libraries: Import the gto and dft modules from pyscf and the this compound library.

  • Define the molecule: Create a pyscf.gto.Mole object to define the molecular geometry and basis set.

  • Initialize the DFT object: Create a pyscf.dft.RKS object for a restricted Kohn-Sham calculation.

  • Set the this compound functional: The key step is to assign the this compound functional to the _numint attribute of the DFT object using this compound.NeuralNumInt.

  • Run the calculation: Execute the kernel() method to perform the self-consistent field (SCF) calculation.

Geometry Optimization

Geometry optimization finds the minimum energy structure of a molecule.

Protocol 3: Geometry Optimization with this compound

  • Import necessary libraries: In addition to the modules for a single-point calculation, import the optimizer from pyscf.geomopt.

  • Define the molecule and DFT object: Follow steps 2-4 from Protocol 2 to set up the molecule and the this compound functional.

  • Run the geometry optimization: Use the optimizer to perform the geometry optimization. PySCF's geomopt module can interface with external optimizers like berny or geometric.

Example Scripts

Below are example Python scripts for running calculations with this compound in PySCF.

Single-Point Energy of a Water Molecule
Geometry Optimization of a Methane Molecule

Visualizations

Workflow for a Single-Point Energy Calculation

SinglePointWorkflow start Start import_libs Import PySCF and this compound start->import_libs define_mol Define Molecule (Geometry, Basis Set) import_libs->define_mol setup_dft Setup RKS Calculation define_mol->setup_dft set_this compound Set this compound Functional mf._numint = this compound.NeuralNumInt(...) setup_dft->set_this compound run_scf Run SCF Calculation (mf.kernel()) set_this compound->run_scf get_energy Obtain Energy run_scf->get_energy end End get_energy->end

Caption: Workflow for a single-point energy calculation using this compound in PySCF.

Workflow for a Geometry Optimization

GeometryOptimizationWorkflow cluster_scf SCF Cycle calculate_forces Calculate Nuclear Gradients update_geometry Update Geometry calculate_forces->update_geometry check_convergence Check Convergence update_geometry->check_convergence check_convergence->calculate_forces Not Converged end End (Optimized Geometry) check_convergence->end Converged start Start setup_calc Setup this compound Calculation (Molecule, Basis, Functional) start->setup_calc initial_scf Initial SCF Calculation setup_calc->initial_scf initial_scf->calculate_forces

Caption: General workflow for a geometry optimization calculation.

References

Troubleshooting & Optimization

Troubleshooting SCF convergence issues with DM21

Author: BenchChem Technical Support Team. Date: November 2025

Technical Support Center: DM21 Functional

Welcome to the technical support center for the DeepMind21 (this compound) functional. This guide provides troubleshooting assistance and frequently asked questions (FAQs) to help researchers, scientists, and drug development professionals address Self-Consistent Field (SCF) convergence issues that may arise during their experiments.

Frequently Asked Questions (FAQs)

Q1: Why does my this compound calculation fail to converge when other functionals work fine?

A1: The this compound functional is based on a neural network, which distinguishes it from traditional, analytical functionals. This neural network approach can result in a non-smooth exchange-correlation potential.[1] This lack of smoothness can cause oscillations in the energy and gradients during the SCF cycle, making convergence more challenging compared to analytical functionals like SCAN or B3LYP.[1] For instance, in a simple H₂ system, the SCAN functional required only 4 SCF iterations for convergence, whereas this compound required 16.[1][2]

Q2: Are convergence issues more common for certain types of molecules?

A2: Yes, convergence difficulties with this compound are particularly pronounced for specific molecular systems.

  • Transition Metal Chemistry (TMC): this compound consistently struggles with SCF convergence for transition metal compounds.[3][4] While it can provide accurate results when it does converge, a significant portion of calculations (around 30% in one study) may fail to reach convergence, limiting its practical use in this area.[3]

  • Systems with Elongated Bonds: Problems have been reported for molecules at or near their dissociation limit. For example, convergence failures have been observed for H₂ and F₂ with bond lengths stretched to approximately 2.3 Å and beyond.[5]

Q3: What are the first troubleshooting steps I should take for a failing this compound SCF calculation?

A3: When encountering a convergence failure, the initial steps should focus on providing a better starting point and stabilizing the SCF procedure.

  • Use a Better Initial Guess: The most effective first step is to use the converged orbitals from a calculation with a more stable, traditional functional (like B3LYP) as the initial guess for your this compound calculation.[3][6]

  • Employ Damping and Level Shifting: For oscillating calculations, introducing damping can help stabilize the SCF procedure. For systems that may have complex electronic structures (like stretched molecules), applying a level shift can help guide the calculation toward the correct electronic state.[5]

Q4: Which SCF algorithms are recommended or not recommended for this compound?

A4: The choice of SCF algorithm is critical. Standard algorithms like Direct Inversion in the Iterative Subspace (DIIS) may struggle with the oscillatory nature of this compound. While second-order SCF methods (like the Newton-Raphson method, or SOSCF in PySCF) are powerful for difficult convergence cases, they are not compatible with this compound.[7] This is because the this compound implementation does not support the second-order derivatives of the exchange-correlation energy required by these methods.[5][7] Even direct orbital optimization methods, which bypass the standard SCF procedure, can fail if the functional is highly non-smooth for the system .[3] Therefore, users should primarily rely on stabilizing first-order methods like DIIS in combination with techniques like a good initial guess, damping, and level shifting.

Q5: How can I resolve convergence failure for systems with stretched bonds?

A5: For molecules with elongated bonds, such as during bond dissociation, the system often adopts a broken-symmetry ground state, which can be difficult for standard SCF algorithms to find. This is a common point of failure for this compound.[5] In these cases, applying a level shift (e.g., a value of 0.5 Hartrees) can be an effective solution. The level shift artificially raises the energy of the virtual orbitals, which can help prevent orbital mixing and guide the SCF procedure to the correct, lower-energy broken-symmetry wavefunction, leading to successful convergence.[5]

Q6: Can I use this compound for periodic systems or with dispersion corrections?

A6: The standard implementation of this compound in PySCF (this compound.NeuralNumInt) is designed for molecular (non-periodic) systems and is not compatible with the periodic boundary condition framework, which requires a different numerical integration interface.[8] Furthermore, applying standard dispersion corrections like Grimme's D3 method may not work directly. This is because this compound is implemented by overloading the numerical integration object (mf._numint) rather than setting the mf.xc attribute, which can interfere with helper functions designed to add dispersion corrections.[9]

Troubleshooting Guides and Protocols

General Troubleshooting Workflow

When a this compound SCF calculation fails to converge, a systematic approach can help identify and resolve the issue. The following diagram outlines a recommended workflow.

start This compound SCF Fails check_guess Use Converged Orbitals from another functional (e.g., B3LYP) as initial guess start->check_guess re_run1 Re-run this compound SCF check_guess->re_run1 check_oscillation Does SCF Energy Oscillate? re_run1->check_oscillation Fails success SCF Converged re_run1->success Converges add_damp_level Apply Damping and/or Level Shifting check_oscillation->add_damp_level Yes check_system Is this a known problematic system? (Transition Metal, Stretched Bond) check_oscillation->check_system No re_run2 Re-run this compound SCF add_damp_level->re_run2 re_run2->check_system Fails re_run2->success Converges advanced_methods Employ Advanced Strategies (See Table 1 & Protocol) check_system->advanced_methods Yes report_issue Consider alternative functional or report issue check_system->report_issue No advanced_methods->success

A general workflow for troubleshooting this compound SCF convergence failures.
Logical Approach for Stretched Bond Issues

Convergence failures in systems with elongated bonds are often related to finding the correct broken-symmetry electronic state. The following diagram illustrates the logic for diagnosing and solving this specific problem.

problem Problem: SCF fails for molecule with elongated bonds (e.g., H₂ at 2.3 Å) cause Likely Cause: Calculation is failing to find the more stable, broken-symmetry wavefunction. problem->cause solution Solution: Apply a level shift to raise the energy of virtual orbitals. cause->solution implementation Implementation (PySCF): mf.level_shift = 0.5 solution->implementation outcome Outcome: Calculation is guided to the correct broken-symmetry state, leading to SCF convergence. implementation->outcome

Logical diagram for solving stretched bond convergence issues with level shifting.

Quantitative Data and Experimental Protocols

Data Presentation

The difficulty of converging this compound can be quantified by comparing the number of SCF iterations against traditional functionals or by examining the success rates of different computational strategies.

Table 1: SCF Convergence Strategies for Transition Metal Chemistry Based on strategies employed for challenging transition metal systems.[3][6]

StrategyMax SCF IterationsConvergence Threshold (Energy)Convergence Threshold (Gradient)Initial Guess
Strategy A 20010⁻⁶ Ha10⁻³ Ha/BohrB3LYP Orbitals
Strategy B 50010⁻⁶ Ha10⁻³ Ha/BohrB3LYP Orbitals
Strategy C 90010⁻⁶ Ha10⁻³ Ha/BohrB3LYP Orbitals

Table 2: Example SCF Iteration Count Comparison For the H₂ molecule in a 6-31G basis set.[1][2]

FunctionalSCF Iterations to Converge
SCAN 4
This compound 16
Experimental Protocols

Below are sample methodologies for implementing troubleshooting techniques within the PySCF computational chemistry package, which is the primary platform for this compound.[10][11]

Protocol 1: Using a B3LYP Initial Guess

This protocol details how to first run a B3LYP calculation and then use its converged density matrix as the initial guess for the this compound calculation.

Protocol 2: Applying Level Shifting and Damping

This protocol shows how to apply level shifting and damping to a this compound calculation in PySCF, which is useful for oscillating systems or those with difficult electronic structures.[5]

References

Technical Support Center: DM21 Functional for Transition Metal Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and answers to frequently asked questions regarding the performance of the DeepMind21 (DM21) density functional for transition metal chemistry. The content is tailored for researchers, computational chemists, and professionals in drug development.

Frequently Asked Questions (FAQs)

Q1: What is the this compound density functional?

A: The DeepMind21 (this compound) functional is a machine-learned density functional approximation (DFA) developed to improve the accuracy of Density Functional Theory (DFT) calculations.[1][2] Unlike traditional "human-designed" functionals, this compound was trained on a large dataset of chemical systems to overcome known deficiencies in standard DFAs, particularly those related to fractional charges and spins.[3]

Q2: Why does this compound fail for transition metal chemistry?

A: The primary and most consistent failure of this compound in transition metal chemistry (TMC) is its inability to achieve self-consistent field (SCF) convergence.[1][4][5] This functional was trained predominantly on main-group chemistry, and its learned features do not extrapolate well to the more complex electronic structures of transition metals.[1][2] This lack of transferability is a significant practical limitation.[3]

Q3: What are the underlying electronic structure challenges with transition metals?

A: Transition metal complexes are notoriously difficult for most DFT functionals, not just this compound. The key challenges include:

  • Self-Interaction Error (SIE): Many approximate functionals incorrectly allow an electron to interact with its own density, an artifact known as self-interaction error.[6] This error can artificially stabilize delocalized electronic states, which is problematic for the localized d-orbitals of transition metals.[6][7]

  • Static (or Strong) Correlation: The near-degeneracy of d-orbitals in many transition metal systems leads to a situation where the single-determinant approximation used in Kohn-Sham DFT is insufficient. This is a major challenge when describing bond breaking, spin states, and excited states.[8][9]

  • Spin-State Energetics: Accurately predicting the small energy differences between different spin states (e.g., high-spin vs. low-spin) is a significant hurdle.[10] The results are often highly sensitive to the functional used, particularly the amount of exact exchange included.[9]

Q4: How accurate is this compound for transition metals when a calculation does converge?

A: When SCF convergence is achieved, this compound can demonstrate accuracy that is comparable to, or even superior to, the widely-used B3LYP functional for transition metal chemistry.[1][2][4] However, the frequent and often insurmountable convergence failures make it an impractical choice for routine, self-consistent calculations in this domain.[1]

Q5: Can the convergence issues be fixed with standard computational chemistry techniques?

A: No, standard techniques for improving SCF convergence (e.g., adjusting damping, level shifting, or using different SCF algorithms) are generally not sufficient to resolve this compound's convergence failures for transition metals.[1] Even more robust methods like direct orbital optimization have been shown to fail, underscoring that the limitation is fundamental to the functional's applicability to this chemical space.[1]

Troubleshooting Guide

Q: My this compound calculation on a transition metal complex failed. What should I do?

A: The most likely cause is a failure to achieve SCF convergence.

  • Verify the Error: Check your output file for messages indicating that the SCF procedure did not converge within the maximum number of allowed cycles.

  • Assess Your Goal:

    • If you require a self-consistent density and orbitals from this compound, the calculation is unlikely to succeed. You should switch to a more reliable functional for transition metals (e.g., B3LYP, PBE0, TPSSh).

    • If you are primarily interested in obtaining a more accurate energy, you can use the this compound functional in a non-self-consistent manner on orbitals from a different, converged calculation. This is the most recommended workaround.

Q: My this compound calculation is not converging. What is the recommended workaround?

A: The recommended and most effective workaround is to evaluate the this compound functional on densities/orbitals obtained from a converged calculation with a different functional, such as B3LYP.[1] This non-self-consistent procedure is often denoted as This compound@B3LYP .

Why this works: This approach leverages the potential accuracy of the this compound functional form while bypassing the problematic self-consistent optimization procedure that consistently fails for transition metals.[1] Studies have shown that the this compound@B3LYP approach can yield noticeably more accurate results than a standard, self-consistent B3LYP calculation.[1]

Q: The geometry optimization with this compound is behaving unexpectedly. Is this related?

A: This may be a separate issue. Research has indicated that numerical noise from the neural network component of this compound can affect the calculation of nuclear gradients.[3][11] This can lead to non-smooth potential energy surfaces and difficulties in geometry optimization, even for systems where SCF convergence is achieved.

Data Presentation

Performance Comparison for Transition Metal Chemistry

The following table summarizes the Mean Absolute Errors (MAEs) in kcal/mol for various computational approaches on transition metal chemistry datasets. The data highlights that while self-consistent this compound struggles, the non-self-consistent this compound@B3LYP method shows significant promise.

MethodDescriptionRepresentative MAE (kcal/mol)Key Takeaway
B3LYP@B3LYP Self-consistent B3LYP calculation.9.36[3]Standard baseline performance.
This compound@this compound Self-consistent this compound calculation (for cases that converge).8.41[3]Slightly more accurate than B3LYP, but often fails to converge.
This compound@B3LYP This compound energy evaluated on converged B3LYP orbitals.8.08 [3]Most accurate and reliable approach, avoiding convergence issues.
B3LYP@this compound B3LYP energy evaluated on converged this compound orbitals.9.04[3]Less accurate than this compound@B3LYP, showing the value of the this compound functional form.

Experimental Protocols

Protocol: this compound@B3LYP Single-Point Energy Calculation

This protocol outlines the steps to obtain a more accurate single-point energy for a transition metal complex using the this compound functional while avoiding its convergence issues. This procedure is valid in quantum chemistry packages that allow for reading orbitals from a previous calculation and performing a single energy evaluation with a different functional.

Objective: To calculate a this compound@B3LYP energy.

Methodology:

  • Step 1: Geometry Optimization with a Robust Functional.

    • Functional: B3LYP (or another functional known to be reliable for transition metal geometries, like PBE0).

    • Basis Set: Choose a suitable basis set for your system (e.g., def2-TZVP).

    • Task: Perform a standard geometry optimization and frequency calculation to obtain a stable, converged geometry.

    • Output: Save the final optimized coordinates and, crucially, the converged molecular orbitals (often in a checkpoint or wavefunction file).

  • Step 2: Non-Self-Consistent this compound Energy Calculation.

    • Setup: Start a new calculation using the optimized geometry from Step 1.

    • Functional: Specify the this compound functional.

    • Task: Set the calculation type to a single-point energy evaluation (SP).

    • SCF Control:

      • Instruct the program to read the initial orbitals from the checkpoint/wavefunction file generated in Step 1.

      • Set the maximum number of SCF cycles to zero or one . This is the critical step that prevents the program from re-optimizing the orbitals and instead forces it to perform only a single energy evaluation using the B3LYP orbitals.

    • Execution: Run the calculation. The resulting energy will be the this compound@B3LYP energy.

Visualizations

Logical Cause of this compound Failure

cluster_origin Origin of this compound cluster_application Application & Failure TrainingData Training Data (Main-Group Chemistry) This compound This compound Functional TrainingData->this compound Trained on TMC Transition Metal Chemistry (Unseen Domain) This compound->TMC Applied to Mismatch Electronic Structure Mismatch (d-orbitals, strong correlation) TMC->Mismatch Features Failure SCF Convergence Failure Mismatch->Failure Leads to Start Start this compound Calculation on Transition Metal System CheckConv Did SCF Converge? Start->CheckConv Success Success: Analyze Results CheckConv->Success Yes Failure Failure: SCF Did Not Converge CheckConv->Failure No Action1 Option 1: Perform this compound@B3LYP (Recommended Workaround) Failure->Action1 Solution Action2 Option 2: Switch to a different functional (e.g., B3LYP, PBE0) Failure->Action2 Alternative

References

Navigating DM21 Geometry Optimization: A Technical Guide

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for the DM21 functional. This guide is designed to assist researchers, scientists, and drug development professionals in optimizing the performance of this compound for geometry optimization tasks. Here, you will find troubleshooting advice and frequently asked questions to address common challenges encountered during your computational experiments.

Frequently Asked Questions (FAQs)

Q1: What is the this compound functional?

A1: this compound is a neural network-based exchange-correlation functional for Density Functional Theory (DFT) developed by DeepMind.[1][2] It is designed to approximate the energy density functional component of DFT, which describes the quantum mechanical behavior of molecules.[1] A key strength of this compound is its ability to address systemic problems found in previous functional approximations, particularly for systems exhibiting "fractional electron character."[1][2]

Q2: In which software is this compound available?

A2: this compound is available as an extension to the PySCF (Python-based Simulations of Chemistry Framework).[1][3]

Q3: How does this compound's performance in energy calculations compare to traditional functionals?

A3: this compound has demonstrated state-of-the-art performance in energy calculation benchmarks, often outperforming traditional hybrid and double-hybrid functionals.[1][2] For instance, on the GMTKN55 benchmark, this compound showed a significantly lower mean absolute error (MAE) compared to the analytical functional SCAN.[3]

Troubleshooting Guide

Issue 1: Slow Geometry Optimization Performance

Symptom: Geometry optimization calculations using this compound are significantly slower compared to traditional functionals like PBE0 or SCAN.[4]

Cause: The primary reason for the slower performance is the computational cost associated with the neural network-based functional and the lack of analytical gradients.[5][6] Geometry optimization with this compound relies on numerical gradients, which require multiple energy evaluations at each optimization step, increasing the overall computational time.[6]

Resolution:

  • Acknowledge the Cost: Be aware that this compound is inherently slower for geometry optimization than many analytical functionals.[4] Plan your computational budget accordingly.

  • Hardware Acceleration: Utilize hardware accelerators such as GPUs if your computational chemistry package and this compound implementation support it.

  • Hybrid Approaches: For an initial geometry, consider using a less computationally expensive functional to get close to the minimum before switching to this compound for final refinement.

Issue 2: Poor Convergence of the Self-Consistent Field (SCF) Cycle

Symptom: The SCF calculation fails to converge or requires an unusually high number of iterations. This is a known issue, particularly for systems containing transition metals.[3][7] For example, a study noted that for the H₂ system, SCF convergence with SCAN required 4 iterations, while this compound required 16.[3]

Cause: The oscillatory or non-smooth behavior of the neural network potential can lead to difficulties in achieving a stable, self-consistent solution for the electron density.[3][5]

Resolution:

  • Initial Guess from a Different Functional: Use the converged orbitals from a calculation with a well-behaved traditional functional (e.g., B3LYP) as the initial guess for the this compound SCF calculation.[7]

  • Convergence Algorithms: Experiment with different SCF convergence algorithms and settings available in your software package. Damping, level-shifting, or Pulay's Direct Inversion of the Iterative Subspace (DIIS) with modified parameters might help.

  • Convergence Thresholds: In some cases, slightly loosening the SCF convergence threshold may be necessary, although this should be done with caution as it can impact the accuracy of the final energy and gradients. For this compound SCF, a convergence threshold of 10⁻⁶ for energy and 10⁻³ for gradients has been used in some studies.[7]

Issue 3: Inaccurate Geometries or Unstable Optimization Trajectories

Symptom: The geometry optimization process oscillates, fails to find a minimum, or results in a molecular geometry that is less accurate than those obtained with traditional functionals.[4][5]

Cause: The non-smooth nature of the this compound potential energy surface can lead to "noisy" or oscillatory gradients.[3][4] This can confuse the optimization algorithm, leading to unstable steps and difficulty in locating the true energy minimum.[3]

Resolution:

  • Adjust the Numerical Differentiation Step: Since this compound often relies on numerical gradients, the step size for the finite difference calculation is crucial. A step size in the range of 0.0001–0.001 Å has been found to produce smoother nuclear gradients.[4]

  • Choice of Optimizer: The performance of different geometry optimization algorithms can vary. If available, try different optimizers (e.g., quasi-Newton methods like BFGS vs. conjugate gradient).

  • Verify the Final Structure: After a geometry optimization converges, it is good practice to perform a frequency calculation to ensure that the obtained structure corresponds to a true minimum (i.e., has no imaginary frequencies).

Data Summary

The following table summarizes the performance of this compound in comparison to other functionals on various benchmarks for energy calculations.

BenchmarkFunctionalMean Absolute Error (kcal/mol)
GMTKN55This compound1.5[3]
SCAN3.6[3]
BBBThis compoundOutperforms SCAN and other hybrid functionals[4]
QM9This compoundOutperforms SCAN and other hybrid functionals[4]

Experimental Protocols

Protocol: Geometry Optimization using this compound in PySCF

This protocol outlines the general steps for performing a geometry optimization calculation with the this compound functional using the PySCF software package.

  • Molecule Definition: Define the molecular geometry, charge, and spin multiplicity within a PySCF script.

  • Mean-Field Object: Create a mean-field object (e.g., scf.RKS) and specify the this compound functional.

  • SCF Calculation: Perform an initial SCF calculation to obtain the electronic energy and molecular orbitals.

    • Troubleshooting Tip: If SCF convergence is an issue, first converge with a different functional (e.g., 'B3LYP') and use the resulting orbitals as an initial guess for the this compound calculation.

  • Gradient Calculation: Obtain the nuclear gradients. Since analytical gradients are not available for this compound, this will typically involve a numerical gradient calculation.

  • Geometry Optimizer: Select a geometry optimization algorithm. The scipy.optimize.minimize function is often used in conjunction with PySCF's energy and gradient functions.

  • Optimization Execution: Run the geometry optimization, which will iteratively update the nuclear coordinates to minimize the total energy.

  • Convergence Check: The optimization will terminate when the change in energy, forces, or geometry between steps falls below a specified threshold.[3]

  • Post-Analysis: Analyze the final optimized geometry. It is recommended to perform a frequency calculation to confirm that the structure is a true minimum.

Visualizations

DM21_Troubleshooting_Workflow cluster_start Start cluster_problem Problem Identification cluster_solutions Troubleshooting Paths cluster_end Resolution start Initiate this compound Geometry Optimization issue Identify Issue start->issue slow_perf Slow Performance issue->slow_perf Speed scf_conv SCF Convergence Failure issue->scf_conv Convergence geom_inacc Inaccurate Geometry issue->geom_inacc Accuracy sol_slow Hybrid Functional Approach Use GPU Acceleration slow_perf->sol_slow sol_scf Use Initial Guess from Another Functional Adjust Convergence Algorithm scf_conv->sol_scf sol_geom Adjust Numerical Differentiation Step Change Optimizer geom_inacc->sol_geom end Successful Optimization sol_slow->end sol_scf->end sol_geom->end

Caption: A flowchart for troubleshooting common this compound geometry optimization issues.

Geometry_Optimization_Cycle start Initial Geometry scf Solve Kohn-Sham Equations (SCF Cycle) start->scf forces Calculate Forces (Numerical Gradients) scf->forces update Update Atomic Positions (Optimizer Step) forces->update check Check Convergence Criteria (Energy, Forces, Geometry) update->check check->scf Not Converged end Converged Geometry check->end Converged

Caption: The iterative cycle of a typical geometry optimization calculation.[3]

References

Technical Support Center: Overcoming Numerical Noise in DM21 Nuclear Gradients

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and answers to frequently asked questions for researchers, scientists, and drug development professionals encountering numerical noise when calculating nuclear gradients with the DM21 density functional.

Troubleshooting Guide

This guide is designed to help you resolve specific issues encountered during your calculations.

Question: My geometry optimization with this compound is failing to converge or is oscillating wildly.

Answer:

This is a common issue stemming from the inherent numerical noise in the this compound functional, which can lead to oscillations on the potential energy surface.[1] Since this compound often lacks analytical gradients, they are calculated numerically, and this noise can be amplified.[1]

Here are steps to troubleshoot this problem:

  • Tighten SCF Convergence Criteria: The noise in the exchange-correlation potential can make achieving self-consistent field (SCF) convergence challenging.[1] Start by tightening the SCF convergence criteria in your quantum chemistry software. This ensures that the electronic density is well-converged before the nuclear gradients are calculated.

  • Increase the Integration Grid Density: The numerical integration grid used to evaluate the exchange-correlation functional is a critical parameter.[2][3] A coarser grid can introduce significant numerical errors. Switch to a finer or "ultrafine" integration grid. While this will increase computational cost, it is often necessary for achieving a smooth potential energy surface.[4]

  • Use a More Robust Optimization Algorithm: Standard optimization algorithms can be sensitive to noise. If available in your software, switch to a more robust optimizer, such as a quasi-Newton method with a trust radius update or a more resilient line search algorithm.

  • Restart from a Perturbed Geometry: If the optimization is stuck in an oscillatory pattern, try slightly perturbing the molecular geometry of the last step and restarting the optimization. This can sometimes help the optimizer escape a noisy region of the potential energy surface.

Question: I am calculating vibrational frequencies with this compound, and the low-frequency modes are noisy or imaginary.

Answer:

Noisy or imaginary low-frequency modes are often a direct consequence of numerical noise in the nuclear gradients. The second derivatives of the energy (the Hessian matrix), which determine the vibrational frequencies, are highly sensitive to small errors in the gradients.

Follow these steps to address this issue:

  • Ensure a Tightly Optimized Geometry: The accuracy of frequency calculations is critically dependent on the quality of the optimized geometry. Re-run your geometry optimization using the tightest possible convergence criteria for both the SCF and the geometry optimization itself. Use a very fine integration grid during this optimization.

  • Use a High-Quality Integration Grid for the Frequency Calculation: Just as with the geometry optimization, a dense integration grid is crucial for the accurate calculation of the Hessian.[4] Ensure that the grid used for the frequency calculation is at least as fine as the one used for the final stages of the geometry optimization.

  • Employ Numerical Differentiation with Caution: If you are calculating the Hessian via numerical differentiation of the analytical gradients (if available) or numerical differentiation of numerically calculated gradients, be aware that this can amplify noise. If possible, use analytical second derivatives if your software and the functional implementation support it. For this compound, this is generally not an option.

Frequently Asked Questions (FAQs)

Question: What is "numerical noise" in the context of the this compound functional?

Answer:

The this compound functional is a machine-learned model, meaning it approximates the exchange-correlation energy based on training data.[5] Unlike traditional, analytically defined functionals, the neural network architecture of this compound can introduce small, high-frequency oscillations into the potential energy surface.[1] This is analogous to fitting a complex curve to a set of data points; the resulting function may pass through all the points but exhibit small wiggles in between. This oscillatory behavior is referred to as numerical noise.[1]

Question: Why are analytical gradients often unavailable for this compound?

Answer:

Analytical gradients require the calculation of the derivative of the exchange-correlation energy with respect to the nuclear coordinates. For a machine-learned functional like this compound, this involves backpropagation through the neural network, which can be complex to implement and computationally expensive.[6] Consequently, many implementations of this compound rely on numerical differentiation to compute nuclear gradients, a process that can be sensitive to the underlying numerical noise of the functional.[1]

Question: How does the choice of integration grid affect numerical noise?

Answer:

In Density Functional Theory (DFT), the exchange-correlation term is calculated by numerical integration on a discrete grid of points around each atom.[2][3] The density and distribution of these grid points determine the accuracy of the integration.

  • Coarse Grids: Have fewer points and are computationally faster, but they can lead to significant integration errors, which manifest as numerical noise. This is particularly problematic in the valence regions far from the nucleus, which are important for weak interactions.[2]

  • Fine/Ultrafine Grids: Have a much higher density of points, leading to more accurate integration and a smoother potential energy surface.[4] This increased accuracy comes at the cost of longer computation times.

For a functional with inherent noise like this compound, using a high-quality integration grid is essential to avoid compounding the functional's own noise with integration errors.

Experimental Protocols

Recommended Protocol for Geometry Optimization with this compound:

  • Initial Structure: Start with a reasonable initial guess for the molecular geometry.

  • SCF Settings:

    • Set a tight SCF convergence criterion (e.g., 10e-8 to 10e-10 Hartree on the energy).

    • Use a robust SCF algorithm, such as DIIS (Direct Inversion in the Iterative Subspace).

  • Integration Grid:

    • For initial optimization cycles, a moderately fine grid (e.g., (75, 302) pruned grid) may be sufficient.

    • For the final convergence, switch to an ultrafine grid (e.g., (99, 590) pruned grid or denser).[4]

  • Optimizer Settings:

    • Use a quasi-Newton optimizer (e.g., BFGS).

    • Set tight convergence criteria for the geometry optimization (e.g., monitoring the maximum force, RMS force, maximum displacement, and RMS displacement).

  • Verification: After convergence, perform a frequency calculation to confirm that the structure is a true minimum (i.e., has no imaginary frequencies). This frequency calculation should also be performed with a fine integration grid.

Data Presentation

Table 1: Impact of Integration Grid Size on Accuracy and Computational Cost

Grid SizeTypical Specification (Radial, Angular Points)Relative Computational CostExpected Accuracy of GradientsRecommended Use Case
Coarse(35, 110)LowLowInitial, rough geometry optimizations
Medium (SG-1)(50, 194)MediumModerateRoutine geometry optimizations
Fine(75, 302)HighHighFinal geometry optimizations, frequency calculations
Ultrafine(99, 590)Very HighVery HighHigh-accuracy frequency calculations, troubleshooting noisy results

Note: The specific grid specifications and keywords will vary depending on the quantum chemistry software package being used.[4]

Mandatory Visualization

cluster_0 Troubleshooting Workflow for this compound Gradient Calculations Start Start: Encountering Convergence Issues or Noisy Results CheckSCF Is SCF Convergence Tight? Start->CheckSCF TightenSCF Action: Tighten SCF Convergence Criteria CheckSCF->TightenSCF No CheckGrid Is the Integration Grid Sufficiently Dense? CheckSCF->CheckGrid Yes TightenSCF->CheckGrid IncreaseGrid Action: Increase Integration Grid Density (e.g., to 'ultrafine') CheckGrid->IncreaseGrid No CheckOptimizer Is the Optimization Algorithm Robust? CheckGrid->CheckOptimizer Yes IncreaseGrid->CheckOptimizer ChangeOptimizer Action: Switch to a More Robust Optimizer CheckOptimizer->ChangeOptimizer No PerturbGeo Action: Perturb Geometry and Restart CheckOptimizer->PerturbGeo Yes ChangeOptimizer->PerturbGeo End End: Converged and Reliable Results PerturbGeo->End

Caption: Troubleshooting workflow for this compound gradient calculations.

cluster_1 Relationship Between Numerical Noise and Calculation Errors MLFunctional This compound as a Machine-Learned Functional Noise Inherent Numerical Noise / Oscillations MLFunctional->Noise NumGrad Numerical Calculation of Gradients Noise->NumGrad InaccurateGrad Inaccurate Nuclear Gradients NumGrad->InaccurateGrad OptIssues Geometry Optimization Problems (e.g., slow convergence, oscillations) InaccurateGrad->OptIssues FreqIssues Incorrect Vibrational Frequencies (e.g., imaginary modes) InaccurateGrad->FreqIssues CoarseGrid Coarse Integration Grid GridError Numerical Integration Errors CoarseGrid->GridError GridError->InaccurateGrad

Caption: The impact of numerical noise on this compound calculations.

References

Navigating DM21 Convergence Failures in Transition Metal Complex Calculations

Author: BenchChem Technical Support Team. Date: November 2025

A Technical Support Guide for Researchers

The DM21 density functional, while powerful for main-group chemistry, frequently presents significant convergence challenges when applied to transition metal complexes (TMCs). This guide provides troubleshooting strategies and answers to frequently asked questions to help researchers, scientists, and drug development professionals navigate these issues and achieve reliable results in their computational experiments.

Frequently Asked Questions (FAQs)

Q1: Why do my this compound calculations for transition metal complexes fail to converge?

A1: The primary reason for this compound convergence failures in TMCs stems from a fundamental limitation in the functional's ability to extrapolate to transition metals.[1] this compound was trained on main-group chemistry, and its machine-learned components can struggle with the complex electronic structures of transition metals. Additionally, as a neural network-based functional, this compound can exhibit non-smooth behavior in the calculation of exchange-correlation energy derivatives, leading to oscillations that hinder convergence.[2][3] These issues are often not resolvable with standard Self-Consistent Field (SCF) setting adjustments.[1]

Q2: Are there specific types of transition metal complexes that are more prone to convergence issues with this compound?

A2: While the literature does not provide an exhaustive list, systems with significant multi-reference character or those that are challenging for even traditional density functionals are likely to be problematic for this compound. A study highlighted that for a dataset of 117 TMC reactions, roughly 30% did not reach SCF convergence with this compound.[1]

Q3: How does this compound's performance on TMCs compare to other functionals like B3LYP?

A3: When this compound calculations do converge, they can offer accuracy comparable to or sometimes better than B3LYP for TMCs.[1] However, B3LYP is generally more robust and less prone to the severe convergence issues that plague this compound in this chemical space.[1] The primary advantage of B3LYP is its reliability in achieving SCF convergence for a wider range of TMCs.

Q4: Can I use the orbitals from a converged B3LYP calculation as a starting guess for my this compound calculation?

A4: Yes, this is a recommended strategy. Using the converged orbitals from a more stable functional like B3LYP can provide a better starting point for the this compound SCF procedure.[1] However, this does not guarantee convergence, as demonstrated in cases like the FeS molecule where this compound failed to converge even with B3LYP-converged orbitals as an initial guess.[1]

Troubleshooting Guide

Systematic Approach to Resolving Convergence Failures

When encountering a this compound convergence failure with a transition metal complex, a systematic approach to troubleshooting is crucial. The following workflow provides a step-by-step guide to diagnose and potentially resolve the issue.

G cluster_0 Initial Calculation Setup cluster_1 Troubleshooting Workflow start Start: this compound Calculation on TMC check_convergence SCF Convergence? start->check_convergence success Success: Converged Result check_convergence->success Yes failure Failure: Convergence Issue check_convergence->failure No b3lyp_guess Run B3LYP Calculation to Convergence failure->b3lyp_guess use_b3lyp_orbitals Use B3LYP Orbitals as Initial Guess for this compound b3lyp_guess->use_b3lyp_orbitals dm21_retry Re-run this compound Calculation use_b3lyp_orbitals->dm21_retry check_convergence2 SCF Convergence? dm21_retry->check_convergence2 check_convergence2->success Yes adjust_scf Adjust SCF Settings (e.g., damping, level shifting) check_convergence2->adjust_scf No dm21_retry2 Re-run this compound with Adjusted SCF adjust_scf->dm21_retry2 check_convergence3 SCF Convergence? dm21_retry2->check_convergence3 check_convergence3->success Yes alternative_functional Consider Alternative Functional (e.g., B3LYP, ωB97X-D) check_convergence3->alternative_functional No

Caption: Troubleshooting workflow for this compound convergence failures in TMCs.

Detailed Experimental and Computational Protocols

Protocol 1: Using a Prior Calculation as an Initial Guess

  • Initial Calculation with a Robust Functional:

    • Set up your calculation using a well-behaved functional such as B3LYP.

    • Ensure the basis set and other computational parameters are consistent with your intended this compound calculation.

    • Run the calculation and ensure it converges to a stable electronic state.

    • Save the converged molecular orbitals or wavefunction file.

  • This compound Calculation with an Initial Guess:

    • In your quantum chemistry software, specify the use of an external file for the initial guess.

    • Provide the path to the saved orbitals from the B3LYP calculation.

    • Set the functional to this compound.

    • Execute the calculation.

Protocol 2: Adjusting SCF Parameters

If the calculation still fails to converge, you can try adjusting the SCF parameters. The specific keywords will vary depending on your software package.

  • SCF Damping: Introduce a damping factor to prevent large oscillations in the electron density between SCF cycles. This can be particularly useful in the initial stages of the calculation.

  • Level Shifting: This technique involves shifting the energies of the virtual orbitals to improve the separation between occupied and virtual orbitals, which can aid convergence.

  • Pulay DIIS (Direct Inversion in the Iterative Subspace): While often a default, ensure that DIIS is enabled and consider adjusting its parameters, such as the size of the subspace.

Quantitative Data Summary

The following table summarizes the convergence behavior of this compound compared to B3LYP on the TMC117 dataset, as reported in the literature.

FunctionalConverged ReactionsNon-Converged ReactionsPercentage of Convergence Failures
This compound 83 out of 11734 out of 117~29%
B3LYP 117 out of 1170 out of 1170%

Data extracted from a study on the application of this compound to transition metal chemistry.[1]

Logical Relationship of Convergence Issues

The convergence difficulties with this compound in the context of TMCs can be visualized as a cascade of interconnected issues.

G cluster_0 Root Cause cluster_1 Direct Consequences cluster_2 Manifestation in Calculations cluster_3 Observed Outcome dm21_training This compound Trained on Main-Group Chemistry extrapolation_limit Poor Extrapolation to Transition Metals dm21_training->extrapolation_limit nonsmooth_potential Non-Smooth Exchange-Correlation Potential dm21_training->nonsmooth_potential scf_instability SCF Instability extrapolation_limit->scf_instability gradient_oscillations Oscillations in Gradients nonsmooth_potential->gradient_oscillations gradient_oscillations->scf_instability convergence_failure This compound Convergence Failure in TMCs scf_instability->convergence_failure

Caption: Causal chain leading to this compound convergence failures for TMCs.

References

DM21 Technical Support Center: Troubleshooting and Optimization

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for the DM21 functional. This guide is designed for researchers, scientists, and drug development professionals to address common challenges and optimize the performance of their this compound computations.

Frequently Asked Questions (FAQs)

Q1: What is the this compound functional?

This compound is a neural network-based exchange-correlation functional for Density Functional Theory (DFT) calculations.[1][2][3] It has demonstrated high accuracy in energy calculations, often outperforming traditional functionals on benchmarks like GMTKN55.[1][4] However, it is computationally more demanding than standard functionals.[1][5]

Q2: Why are my this compound calculations so slow?

The increased computational cost of this compound stems from two main factors: the necessity of computing two-electron integrals at each grid point and challenges in achieving Self-Consistent Field (SCF) convergence.[1][6] For smaller molecular systems, this compound can be even slower than more computationally intensive methods like CCSD(T).[1][6]

Q3: I'm encountering SCF convergence issues with this compound. What can I do?

SCF convergence problems are a known issue with this compound, particularly for transition metal chemistry and systems with elongated bonds.[5][7] Here are several strategies to address this:

  • Use a robust SCF protocol: Start with a standard SCF approach and progressively move to more robust strategies if convergence is not met. A suggested protocol involves adjusting level shifting, damping factors, and the start of the Direct Inversion in the Iterative Subspace (DIIS) algorithm.[8]

  • Employ a level shift: Applying a level shift can help stabilize convergence, especially in cases of orbital oscillation.[7]

  • Use orbitals from a previous calculation: You can use the converged orbitals from a calculation with a more stable functional (like B3LYP) as an initial guess for your this compound calculation.[5][8]

  • Check for small HOMO-LUMO gaps: Small energy gaps between the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) can lead to convergence instability.[9]

Q4: My geometry optimization with this compound is unstable or failing. Why is this happening?

The oscillatory nature of the neural network in this compound can lead to noisy potential energy surfaces, which in turn causes instability in geometry optimizations.[1][5] This can result in difficulties in finding the true energy minimum.

Q5: How can I improve the stability of my this compound geometry optimizations?

To mitigate the issues arising from the oscillatory behavior of this compound, it is crucial to carefully select the numerical differentiation step size for gradient calculations. A step size in the range of 0.0001–0.001 Å has been found to produce smoother nuclear gradients.[5][10][11]

Troubleshooting Guide

This guide provides solutions to specific error messages and common problems encountered during this compound experiments.

Issue/Error MessagePotential CauseSuggested Solution
SCF not converged Small HOMO-LUMO gap, orbital oscillation, poor initial guess.1. Implement a robust SCF convergence protocol (see FAQ 3). 2. Use SCF=vshift=x (where x is typically 300-500) to apply a level shift. 3. Use guess=read to provide orbitals from a previously converged calculation with a different functional.[5][8]
Geometry optimization fails to find a minimum or oscillates. Noisy potential energy surface due to the oscillatory nature of the this compound functional.Adjust the numerical differentiation step for gradient calculations. A step size between 0.0001 and 0.001 Å is recommended.[5][10][11]
Slow performance on small to medium-sized molecules. Inherent computational cost of the this compound functional.Be aware that for smaller systems, this compound can be slower than traditional methods.[1][5] For larger systems, performance may be more competitive, but this is an area of ongoing research.
Convergence issues with transition metals. This compound can struggle with the electronic structure of transition metal complexes.Use a converged wavefunction from a functional known to perform well for transition metals (e.g., B3LYP) as an initial guess.[5][8] Be prepared for a significant number of SCF cycles.

Performance Benchmarks

Comparison MetricThis compound PerformanceTraditional Functionals (e.g., PBE0, SCAN)High-Accuracy Methods (e.g., CCSD(T))
Energy Accuracy (GMTKN55) High (MAE ~1.5 kcal/mol)[1]Moderate (MAE ~3.6 kcal/mol for SCAN)[1]Very High (Reference)
Computational Time (Single Point) Significantly Slower[1]FasterCan be faster for small systems[1][6]
Geometry Optimization Accuracy Does not consistently outperform analytical functionals[5]Generally reliableHigh
SCF Convergence Can be challenging, especially for certain systems[5][7]Generally robustNot applicable (not an iterative SCF method)

MAE: Mean Absolute Error

Experimental Protocols

Protocol 1: Single-Point Energy Calculation with this compound in PySCF

This protocol outlines the steps for performing a single-point energy calculation using the this compound functional within the PySCF framework.

  • System Setup: Define the molecular geometry and basis set using the gto module in PySCF.

  • Mean-Field Object: Create a mean-field object (e.g., RKS for restricted Kohn-Sham).

  • Specify this compound Functional: Assign the this compound functional to the mean-field object. This is typically done by setting the .xc attribute to 'this compound'.

  • Run Calculation: Execute the kernel() method of the mean-field object to perform the SCF calculation.

  • Check Convergence: Verify that the calculation has converged by checking the .e_tot and .converged attributes of the mean-field object.

  • Troubleshooting: If the calculation fails to converge, implement the strategies outlined in the Troubleshooting Guide, such as using a level shift or providing a better initial guess.

Protocol 2: Geometry Optimization with this compound in PySCF

This protocol provides a general workflow for performing geometry optimization using the this compound functional.

  • System Setup: As with a single-point calculation, define the molecule and basis set.

  • Mean-Field Object: Create a mean-field object and specify the this compound functional.

  • Geometry Optimizer: Obtain a geometry optimizer object from the mean-field object using the .Gradients() method followed by .as_scanner().

  • Run Optimization: Call the optimizer object with the molecule object as an argument to start the optimization.

  • Monitor Convergence: The optimization will iteratively update the geometry to find an energy minimum. Monitor the convergence of both the SCF at each step and the overall geometry.

  • Adjust Numerical Gradient Step: If the optimization is unstable, it is critical to adjust the step size for the numerical differentiation of the gradients. This is a key parameter for successful this compound geometry optimizations.[5][10][11]

Visualizations

DM21_Troubleshooting_Workflow start Start this compound Calculation scf Perform SCF Calculation start->scf check_scf SCF Converged? scf->check_scf geom_opt Perform Geometry Optimization Step check_scf->geom_opt Yes troubleshoot_scf Troubleshoot SCF (Level Shift, Guess, etc.) check_scf->troubleshoot_scf No check_geom Geometry Converged? geom_opt->check_geom troubleshoot_geom Adjust Numerical Gradient Step Size geom_opt->troubleshoot_geom check_geom->scf No end End Calculation check_geom->end Yes troubleshoot_scf->scf

Caption: A workflow for troubleshooting this compound calculations.

DFT_Geometry_Optimization start_geom Initial Molecular Geometry solve_ks Solve Kohn-Sham Equations (SCF) start_geom->solve_ks calc_forces Calculate Nuclear Forces (Gradients) solve_ks->calc_forces update_geom Update Atomic Positions calc_forces->update_geom check_convergence Check Convergence Criteria (Energy, Forces, Geometry) update_geom->check_convergence check_convergence->solve_ks Not Converged final_geom Optimized Geometry check_convergence->final_geom Converged

Caption: The iterative process of DFT geometry optimization.[6]

References

Limitations of the DM21 functional for certain molecules

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for the DM21 density functional. This guide is designed for researchers, scientists, and drug development professionals who are using or considering using the this compound functional in their computational experiments. Here you will find troubleshooting guides and frequently asked questions (FAQs) to address specific issues you may encounter.

Frequently Asked Questions (FAQs)

Q1: My Self-Consistent Field (SCF) calculation for a transition metal complex is failing to converge with this compound. What should I do?

A1: SCF convergence failure is a known limitation of the this compound functional, particularly for transition metal chemistry (TMC)[1][2][3]. The functional was trained on main-group chemistry and its ability to extrapolate to transition metals is limited[1].

Troubleshooting Steps:

  • Use a Different Initial Guess: Obtain orbitals from a converged SCF calculation with a more robust functional (e.g., B3LYP) and use these as the initial guess for your this compound calculation[1].

  • Employ Orbital Optimization Algorithms: If standard SCF procedures fail, consider using a direct orbital optimization algorithm. However, be aware that even these advanced methods may not resolve the convergence issues for some TMC systems with this compound[1].

  • Adjust SCF Settings: While standard adjustments may not always work, you can try increasing the maximum number of SCF iterations or using level-shifting techniques, which have been reported to help in cases of elongated bonds[1][4].

  • Consider a Hybrid Approach: As a workaround, you can perform a single-point energy calculation with this compound using the converged orbitals from another functional (e.g., this compound@B3LYP)[1]. This has shown to sometimes yield improved accuracy over the baseline functional[1].

Q2: I am performing a geometry optimization, and the results with this compound are not as accurate as expected compared to other functionals. Why is this happening?

A2: The this compound functional can exhibit oscillatory behavior or "numerical noise" on the potential energy surface, which can negatively impact the calculation of nuclear gradients required for geometry optimization[5][6]. This can lead to less accurate optimized geometries compared to traditional analytical functionals like PBE0 or SCAN[5][6]. While this compound may show competitive performance for energy calculations, this does not always translate to superior geometry optimizations[5].

Troubleshooting Steps:

  • Verify Applicability: Ensure that the molecules you are studying are well-represented by the main-group chemistry in this compound's training set[5].

  • Use a Different Functional for Geometries: A common and effective strategy is to perform the geometry optimization with a reliable and computationally less expensive functional (e.g., B3LYP, PBE0) and then perform a final single-point energy calculation with this compound on the optimized geometry.

  • Numerical Differentiation Step: If you must optimize with this compound, it has been found that a numerical differentiation step in the range of 0.0001-0.001 Å can help obtain smoother nuclear gradients[6].

Q3: My this compound calculation is running very slowly. Is this normal?

A3: Yes, it is a known characteristic that this compound calculations can be significantly more computationally expensive than those with traditional functionals[1][6][7]. A single SCF iteration with this compound can take substantially longer than a full, converged calculation with a functional like B3LYP[1]. This is due to the complexity of evaluating the neural network-based functional.

Q4: I am trying to use this compound with a dispersion correction (e.g., D3), but my calculation is failing. What is the issue?

A4: There have been documented issues with the implementation of this compound in PySCF that can cause conflicts when used with dispersion corrections like D3[8]. The way the this compound functional is set up in the software can interfere with how dispersion corrections are typically applied[8].

Troubleshooting Steps:

  • Consult Documentation: Check the latest documentation for your quantum chemistry software package for specific instructions or workarounds for using this compound with dispersion corrections.

  • Manual Correction: If an integrated approach is not working, you may need to calculate the dispersion correction separately and add it to the final this compound energy.

Q5: Can I use the this compound functional for calculations on periodic systems?

A5: The current implementation of this compound in PySCF is primarily designed for molecular (non-periodic) systems[9]. Using it for periodic systems may lead to errors due to differences in the numerical integration interfaces for periodic and non-periodic calculations[9].

Performance Summary for this compound

The following table summarizes the known limitations of the this compound functional for certain molecular systems and tasks.

Area of Limitation Description of Issue Affected Molecules/Tasks Quantitative Data (Mean Absolute Error - MAE)
Transition Metal Chemistry Consistent struggles with SCF convergence.[1][2][3] The functional was not trained on elements heavier than Krypton.[1]Transition Metal ComplexesFor converged systems, the median error can be around 2.6 kcal/mol. For non-converged systems, errors are arbitrarily set to 50 kcal/mol to highlight the failure.[1]
Geometry Optimization Does not consistently outperform traditional functionals like PBE0 and SCAN.[5][6] This is due to oscillatory behavior in the potential energy surface.[5][6]General Molecules, especially those not in the training set.MAE in bond lengths is generally below 2 pm, but in many cases, PBE0 or SCAN show better performance.[5]
Computational Cost Significantly slower than traditional functionals.[1][6][7]All calculationsA single SCF cycle can be much more time-consuming than a full calculation with functionals like B3LYP or even B2PLYP.[1]
Extrapolation As a machine-learned functional, its performance on molecules and chemical environments not present in its training data is not guaranteed.[3][5]Molecules with elements heavier than Krypton, novel chemical structures.The issues with transition metal chemistry serve as a key example of poor extrapolation.[1][3]

Experimental Protocols

Methodology for Assessing SCF Convergence in Transition Metal Chemistry

To quantitatively assess the convergence behavior of this compound for transition metal complexes, the following computational protocol is typically employed[1]:

  • System Selection: A benchmark set of transition metal complexes and reaction energies is chosen (e.g., the TMC117 dataset).

  • Initial Guess: For this compound calculations, orbitals obtained from a converged B3LYP calculation are used as the initial guess.

  • SCF Settings:

    • Convergence Thresholds: Set to 10⁻⁶ for the energy and 10⁻³ for the gradients in this compound SCF calculations. For B3LYP, tighter thresholds of 10⁻⁸ and 10⁻⁴, respectively, are used.

    • Maximum Iterations: The maximum number of SCF iterations is systematically increased (e.g., 200, 500, 900) to test for convergence.

  • Analysis: The number of systems that fail to converge within the maximum number of iterations is recorded. For converged systems, the reaction energies are compared to high-level reference data to calculate metrics like Mean Absolute Error (MAE).

Troubleshooting Workflow

The following diagram illustrates a general workflow for troubleshooting issues with the this compound functional.

DM21_Troubleshooting start Start this compound Calculation check_convergence Does the SCF Converge? start->check_convergence check_molecule_type Is it a Transition Metal Complex? check_convergence->check_molecule_type No check_geometry Is this a Geometry Optimization? check_convergence->check_geometry Yes use_b3lyp_guess Use B3LYP Orbitals as Initial Guess check_molecule_type->use_b3lyp_guess Yes report_issue Consult Documentation or Report Issue check_molecule_type->report_issue No use_b3lyp_guess->check_convergence analyze_results Analyze Results check_geometry->analyze_results No use_alt_functional Consider Alternative Functional (e.g., PBE0, SCAN) for Geometry check_geometry->use_alt_functional Yes end End analyze_results->end single_point_this compound Perform Single-Point this compound Calculation on Optimized Geometry use_alt_functional->single_point_this compound single_point_this compound->analyze_results

Caption: A flowchart for troubleshooting common issues encountered with the this compound functional.

References

Technical Support Center: Navigating Oscillatory Behavior in DM21 Predictions

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals encountering oscillatory behavior in predictions using the DM21 functional.

Troubleshooting Guide

Unstable or oscillatory predictions during geometry optimization can be a significant hurdle. This guide provides a step-by-step approach to identify, diagnose, and mitigate these issues.

Question: My geometry optimization with this compound is not converging or the energy/forces are fluctuating wildly. What should I do?

Answer: Oscillatory behavior is a known characteristic of the this compound neural network functional, which can arise from the non-smooth nature of the potential energy surface it generates. This can lead to noisy gradients and hinder convergence.[1][2][3][4][5] Follow this troubleshooting workflow to address the issue:

TroubleshootingWorkflow cluster_start Start: Convergence Issues cluster_analysis Analysis cluster_mitigation Mitigation Steps cluster_evaluation Evaluation cluster_end Resolution Start Convergence Failure or High Fluctuations Analyze Analyze Optimization Trajectory (Energy, Forces, Geometry) Start->Analyze CheckOscillations Are Energy/Forces Oscillating? Analyze->CheckOscillations AdjustStep Adjust Numerical Differentiation Step CheckOscillations->AdjustStep Yes Rerun Rerun Optimization CheckOscillations->Rerun No (Other Issue) CheckCoords Review Coordinate System (Prefer Redundant Internals) AdjustStep->CheckCoords InitialGuess Refine Initial Geometry (Use Lower-Level Theory) CheckCoords->InitialGuess TightenSCF Tighten SCF Convergence Criteria InitialGuess->TightenSCF TightenSCF->Rerun CheckConvergence Converged? Rerun->CheckConvergence Success Successful Optimization CheckConvergence->Success Yes Failure Consider Alternative Functional CheckConvergence->Failure No

Caption: Troubleshooting workflow for this compound convergence issues.

Frequently Asked Questions (FAQs)

1. What is oscillatory behavior in this compound and what causes it?

Oscillatory behavior in the context of this compound, a neural network-based exchange-correlation functional, refers to the non-smooth prediction of the potential energy surface (PES). This can manifest as high-frequency oscillations in the calculated energies and their gradients (forces) with small changes in molecular geometry.[1][6][7] This is a known challenge with some neural network functionals and is attributed to the nature of the neural network's interpolation.[1][2][3][4][5]

2. How does this oscillatory behavior impact my drug discovery research?

In drug discovery, accurate determination of the three-dimensional structure of a molecule is crucial for understanding its interaction with a biological target. Geometry optimization is the computational method used to find the most stable structure (a minimum on the PES). If the PES is not smooth, the optimization algorithm may struggle to find the true minimum, leading to:

  • Convergence failure: The optimization may not reach a stable endpoint.

  • Inaccurate geometries: The predicted stable structure may be incorrect, which can mislead subsequent docking or molecular dynamics studies.[6][7]

  • Increased computational cost: The optimization may take an excessive number of steps.

3. When should I be most concerned about these oscillations?

You should be particularly cautious when:

  • Your geometry optimization fails to converge.

  • You observe large fluctuations in energy and forces between optimization steps.

  • You are studying systems that are sensitive to small geometric changes, such as weakly bound complexes or molecules with flexible dihedral angles.

  • The system you are studying is significantly different from the molecules included in the this compound training set.[6][7]

4. Are there specific parameter adjustments I can make to mitigate this issue?

Yes. A key parameter to adjust is the numerical differentiation step size used to calculate the nuclear gradients. For this compound, a step size in the range of 0.0001 to 0.001 Å has been shown to produce smoother gradients, which can significantly improve the stability of the geometry optimization.[2][3][4][5]

5. Does this compound's high accuracy in energy prediction guarantee accurate geometries?

No. While this compound has demonstrated high accuracy in energy calculations for many systems, this does not automatically translate to high accuracy in geometry optimization.[1][6] Geometry optimization relies on accurate gradients of the energy, which can be affected by the oscillatory nature of the this compound-predicted PES.

Quantitative Data Summary

The following table summarizes the performance of this compound in geometry optimization compared to other functionals on the LMGB35 benchmark, as reported in a recent study. The metric shown is the Mean Absolute Error (MAE) in bond lengths, a measure of the accuracy of the predicted geometries.

FunctionalMean Absolute Error (MAE) in Bond Lengths (pm)
This compound Varies, can be below 2 pm for some molecules
PBE0 Generally performs well, sometimes outperforming this compound
SCAN Generally performs well, sometimes outperforming this compound

Note: Lower MAE values indicate higher accuracy in predicting molecular geometries. Performance can be molecule-dependent. For some hydrocarbons, this compound showed a lower MAE than PBE0 and SCAN, while for other molecules, the opposite was true.[6]

Experimental Protocols

Protocol for Geometry Optimization with this compound

This protocol outlines a best-practice approach for performing geometry optimization using the this compound functional, with specific steps to address potential oscillatory behavior.

ExperimentalProtocol cluster_prep Preparation cluster_setup Calculation Setup cluster_run Execution and Monitoring cluster_post Post-Processing InitialGeom 1. Prepare Initial Geometry (e.g., from a lower-level method like semi-empirical) Selectthis compound 2. Select this compound Functional and an appropriate basis set InitialGeom->Selectthis compound SetCoords 3. Specify Redundant Internal Coordinates Selectthis compound->SetCoords SetNumDiff 4. Set Numerical Differentiation Step Size (0.0001 - 0.001 Å) SetCoords->SetNumDiff SetConvergence 5. Define Convergence Criteria (Energy, Force, Displacement) SetNumDiff->SetConvergence RunOpt 6. Run Geometry Optimization SetConvergence->RunOpt Monitor 7. Monitor Convergence (Check for oscillations) RunOpt->Monitor FreqCalc 8. Perform Frequency Calculation (Confirm minimum) Monitor->FreqCalc AnalyzeResults 9. Analyze Final Geometry and Vibrational Modes FreqCalc->AnalyzeResults

Caption: Recommended workflow for this compound geometry optimization.

Detailed Steps:

  • Prepare Initial Geometry: Start with a reasonable initial structure. Pre-optimizing the geometry with a less computationally expensive method (e.g., a semi-empirical method or a smaller basis set DFT calculation) can provide a good starting point and reduce the number of optimization cycles.[8]

  • Select this compound Functional: In your quantum chemistry software package, specify this compound as the exchange-correlation functional. Choose a suitable basis set for your system.

  • Specify Coordinate System: Whenever possible, use redundant internal coordinates for the geometry optimization. This is often the default and most efficient choice for molecular systems.[9]

  • Set Numerical Differentiation Step Size: This is a critical step for this compound. In the input file for your calculation, locate the option for the step size used in the numerical differentiation for gradient calculations and set it to a value between 0.0001 and 0.001 Å.[2][3][4][5]

  • Define Convergence Criteria: Set appropriate convergence criteria for the change in energy, the maximum force, and the root-mean-square of the forces between optimization steps. Tighter convergence criteria for the Self-Consistent Field (SCF) procedure can also improve the accuracy of the forces.[10][11]

  • Run Geometry Optimization: Execute the calculation.

  • Monitor Convergence: During the optimization, monitor the energy, forces, and geometric parameters. If you observe oscillations where these values do not consistently decrease, you may need to stop the calculation and revisit the setup, particularly the numerical differentiation step size.[8]

  • Perform Frequency Calculation: After a successful geometry optimization, it is crucial to perform a frequency calculation. The absence of imaginary frequencies will confirm that the optimized structure is a true minimum on the potential energy surface.[12]

  • Analyze Final Geometry: Analyze the final optimized geometry and vibrational modes to ensure they are chemically reasonable.

References

Technical Support Center: Troubleshooting Slow Calculations with the DM21 Functional

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for researchers, scientists, and drug development professionals. This guide provides troubleshooting advice and frequently asked questions (FAQs) to address slow computational performance when using the DM21 functional in your experiments.

Frequently Asked Questions (FAQs)

Q1: Why are my this compound calculations running so slowly?

Several factors can contribute to slow calculations with the this compound functional. It's important to understand that this compound, as a neural network-based functional, has an inherently high computational cost.[1][2] Here are some of the primary reasons for slow performance:

  • Inherent Computational Cost of this compound: The current implementation of the this compound functional is computationally very demanding.[3] For smaller systems, a single self-consistent field (SCF) iteration with this compound can be more time-consuming than a coupled-cluster singles and doubles with perturbative triples (CCSD(T)) calculation.[4][5]

  • Nature of Meta-GGA Functionals: this compound is a meta-GGA functional. Meta-GGAs are more computationally intensive than simpler functionals like Generalized Gradient Approximations (GGAs) because they include the kinetic energy density as a variable.[6] While they offer improved accuracy, this comes at the cost of increased computational time.[6][7]

  • Numerical Instability and Convergence Issues: Meta-GGA functionals, and particularly neural network-based functionals like this compound, can sometimes exhibit numerical instabilities.[1][6] These can lead to difficulties in achieving self-consistent field (SCF) convergence, resulting in a higher number of iterations and longer calculation times.[8][9]

  • Inadequate Computational Resources: Density Functional Theory (DFT) calculations, especially with complex functionals, are resource-intensive. Insufficient CPU speed, a low number of cores, or limited RAM can significantly slow down your calculations.[10]

  • Suboptimal Calculation Settings: The choice of basis set and the size of the integration grid are critical for both accuracy and computational speed. Using an unnecessarily large basis set or an overly dense integration grid can drastically increase calculation time.[9][11]

Q2: How does the computational cost of this compound compare to other functionals?

Direct, extensive benchmarks for the this compound functional are still emerging. However, based on available information and the general hierarchy of DFT functionals, we can summarize the expected computational cost. Meta-GGA functionals like this compound are computationally more demanding than GGAs.[6] Some studies suggest that numerically stable meta-GGAs can be about three times more expensive than a GGA, while being significantly faster than hybrid functionals.[12]

Functional ClassRelative Computational CostKey Characteristics
Local Density Approximation (LDA)LowDepends only on the electron density. Generally the fastest but least accurate.
Generalized Gradient Approx. (GGA)Low to ModerateUses the electron density and its gradient. A good balance of cost and accuracy for many systems.
Meta-GGA (e.g., this compound) Moderate to High Includes the kinetic energy density. Generally more accurate than GGAs but at a higher computational cost.[6] Can be sensitive to the integration grid.[9]
Hybrid FunctionalsHighMixes a portion of exact Hartree-Fock exchange with a GGA or meta-GGA functional. Often more accurate but significantly slower.
Double-Hybrid FunctionalsVery HighIncorporates a portion of second-order Møller-Plesset (MP2) correlation. Computationally very expensive.

This table provides a generalized comparison. Actual performance can vary based on the specific functional, software implementation, and the system being studied.

Troubleshooting Guide

Issue: My geometry optimization with this compound is extremely slow or failing to converge.

Workflow for Troubleshooting Slow this compound Calculations:

troubleshooting_workflow cluster_convergence Convergence Solutions cluster_settings Settings Optimization cluster_hardware Hardware Considerations start Slow this compound Calculation check_convergence Check SCF Convergence start->check_convergence convergence_issue Address Convergence Issues check_convergence->convergence_issue No convergence_ok SCF Converges but is Slow check_convergence->convergence_ok Yes optimize_settings Optimize Calculation Settings convergence_issue->optimize_settings conv_sol1 Improve Initial Guess convergence_issue->conv_sol1 hardware_review Review Hardware Resources optimize_settings->hardware_review Optimized settings_ok Settings Optimized set_sol1 Adjust Integration Grid optimize_settings->set_sol1 hardware_ok Sufficient Hardware end_slow Accept Inherent Cost of this compound hardware_review->end_slow Sufficient hw_sol1 Utilize High-Frequency CPUs hardware_review->hw_sol1 convergence_ok->optimize_settings conv_sol2 Use Damping/Mixing conv_sol1->conv_sol2 conv_sol3 Increase SCF Iterations conv_sol2->conv_sol3 set_sol2 Choose Appropriate Basis Set set_sol1->set_sol2 set_sol3 Pre-optimize with a Cheaper Method set_sol2->set_sol3 hw_sol2 Increase RAM hw_sol1->hw_sol2 hw_sol3 Consider GPU Acceleration (for specific codes) hw_sol2->hw_sol3

Caption: A step-by-step workflow for diagnosing and addressing slow this compound calculations.

Detailed Methodologies:

  • Addressing SCF Convergence Failure:

    • Improve the Initial Guess: A good starting geometry is crucial. Pre-optimize your molecular structure with a less computationally demanding method, such as a semi-empirical method or a GGA functional, before running the this compound calculation.[10]

    • SCF Convergence Algorithms: If the SCF is oscillating, try using damping or mixing techniques.[8] Many quantum chemistry packages have keywords to control these parameters.

    • Increase Maximum SCF Cycles: In cases of slow convergence, increasing the maximum number of SCF iterations can be helpful. However, if the calculation doesn't converge after a reasonable number of steps, there might be an underlying issue with the input or the system itself.[8]

  • Optimizing Calculation Settings:

    • Integration Grid: Meta-GGA functionals are often highly sensitive to the integration grid.[9][13] Using a grid that is too small can lead to inaccurate results and convergence problems. Conversely, an overly dense grid will significantly slow down the calculation.[11] It is recommended to start with the default "fine" grid in most software packages and increase it if you encounter issues. For this compound and other sensitive functionals, using a larger grid, such as one with (99,590) points, may be necessary to obtain reliable results.[9]

    • Basis Set Selection: Start with a smaller basis set for initial optimizations and then refine your results with a larger basis set.[10] For routine calculations, double-zeta basis sets with polarization functions (e.g., def2-SVP) are often a good starting point. For higher accuracy, triple-zeta basis sets (e.g., def2-TZVP) can be used, but be aware of the increased computational cost.

    • Multi-Step Calculations: For complex structures, consider a multi-step approach. Begin with a smaller basis set and gradually increase its size in subsequent calculations.[10]

  • Hardware and Software Considerations:

    • CPU Performance: DFT calculations often benefit more from higher single-core CPU performance (frequency) than from a very large number of cores with lower individual performance.[10]

    • GPU Acceleration: Some modern DFT codes can leverage GPUs to accelerate calculations, particularly for periodic systems with plane-wave basis sets.[10][14] Check if your software package and calculation type can benefit from GPU acceleration.

    • Memory (RAM): For smaller molecules, ensuring sufficient RAM to use "in-core" algorithms (where two-electron integrals are stored in memory) can significantly speed up calculations.[10]

Q3: Are there any known issues with the this compound functional that could cause slow calculations?

Yes, as a neural network-based functional, this compound can exhibit some specific behaviors that impact performance:

  • Numerical Noise: The output of the neural network can have a degree of numerical noise, which can make it challenging to obtain smooth potential energy surfaces. This can complicate geometry optimizations and require a careful choice of numerical differentiation steps.[2][5]

  • Oscillatory Behavior: Neural network functionals can sometimes show oscillatory behavior, which can also lead to convergence problems during geometry optimization.[1]

If you suspect these issues are affecting your calculations, it is crucial to ensure you are using a recent version of your quantum chemistry software, as implementations and algorithms are continually improving.

Disclaimer: The information provided in this technical support guide is for informational purposes only. The computational cost and performance of the this compound functional may vary depending on the specific software implementation, hardware, and the molecular system under investigation.

References

Debugging DM21 errors in PySCF environment

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for the DM21 functional in the PySCF environment. This guide provides answers to common questions and troubleshooting advice to assist researchers, scientists, and drug development professionals in their computational experiments.

Frequently Asked Questions (FAQs)

Q1: Why is my calculation failing when using Newton or SOSCF convergence methods with this compound?

A1: You may encounter errors when attempting to use second-order optimization algorithms like the Newton-Raphson or Second-Order Self-Consistent Field (SOSCF) methods with the this compound functional. This is because the this compound functional, as implemented in the PySCF-DM21 interface, does not support the computation of second-order derivatives (Hessians) required by these methods.[1] It is recommended to use first-order optimization algorithms.

Q2: Can I use the this compound functional for calculations on periodic systems?

A2: No, the this compound.NeuralNumInt class is designed exclusively for molecular systems and is not compatible with periodic boundary condition (PBC) calculations in PySCF.[2] The numerical integration interface for periodic systems in PySCF differs from the one for molecules, leading to errors if used interchangeably.[2]

Q3: My SCF calculation is failing to converge, particularly when studying bond dissociation. What are the possible reasons and solutions?

A3: Convergence issues, especially for systems with stretched bonds, have been reported with the this compound functional.[3] For instance, convergence failures were observed for H₂ and F₂ dissociation beyond a certain bond length (e.g., 2.3 Angstroms).[3] This behavior can be sensitive to the electronic structure at stretched geometries. The original research on this compound utilized a custom optimization algorithm to handle fractional occupations, which may be necessary for achieving convergence in these challenging cases.[3] For standard calculations, you may try starting from a converged density matrix from a different functional or adjusting the SCF convergence parameters.

Q4: Is it possible to perform geometry optimization with the this compound functional in PySCF?

A4: Standard geometry optimization is not natively supported with the this compound functional in the public release. The required nuclear gradients for the this compound functional are not available out-of-the-box.[4] However, recent research has focused on implementing and evaluating geometry optimization with this compound, suggesting that custom implementations may be possible.[5] Users interested in this functionality should refer to the latest research literature for potential implementation strategies.[5]

Q5: I am receiving a warning message: "Support for int1e_grids not found". How can I resolve this?

A5: This warning indicates an issue with the underlying libraries, specifically libcint and pyscf, not meeting the version requirements for optimized integral calculations.[6] This can lead to slower performance as the calculation falls back to a less efficient loop over grid points.[6] This issue has been observed when PySCF is installed via conda. To resolve this, it is recommended to install PySCF using pip:

This typically ensures that the correct dependencies are met.[6]

This compound Feature Compatibility in PySCF

The table below summarizes the compatibility of the this compound functional with various features and calculation types within the PySCF environment based on user-reported issues.

Feature/Calculation TypeCompatibilityNotes
Molecular Systems Compatible The primary intended use case for the this compound functional in PySCF.
Periodic Systems (PBC) Not Compatible The this compound.NeuralNumInt interface is not designed for periodic calculations.[2]
First-Order SCF Solvers Compatible Standard SCF convergence algorithms can be used.
Newton/SOSCF Solvers Not Compatible Second-order derivatives are not supported.[1]
Geometry Optimization Not Natively Supported Requires custom implementation of nuclear gradients.[4][5]
Stretched Geometries Potential Convergence Issues May require specialized optimization algorithms for fractional occupations.[3]

Methodologies

Standard Protocol for a Single-Point Energy Calculation with this compound

This protocol outlines the basic steps to perform a single-point energy calculation on a molecular system using the this compound functional in PySCF.

  • Import necessary libraries:

  • Define the molecule:

  • Initialize the DFT object:

  • Assign the this compound functional: The core step is to replace the default numerical integration object with the NeuralNumInt from the this compound library.

  • Set convergence parameters (optional but recommended): For potentially difficult systems, tightening the convergence criteria can be helpful.

  • Run the calculation:

Visualizations

Troubleshooting Workflow for this compound Errors

start Start: this compound Calculation Error check_calc_type Check Calculation Type start->check_calc_type check_solver Check SCF Solver check_calc_type->check_solver No (Molecular) is_periodic Periodic System? check_calc_type->is_periodic Yes check_geom Investigate Geometry check_solver->check_geom No is_newton Using Newton/SOSCF? check_solver->is_newton Yes check_install Check Installation/Warnings check_geom->check_install No is_stretched Stretched Bond? check_geom->is_stretched Yes is_warning 'int1e_grids' warning? check_install->is_warning Yes end Consult Documentation/ Further Investigation check_install->end No solution_periodic Solution: this compound not compatible with periodic systems. is_periodic->solution_periodic solution_solver Solution: Use a first-order SCF solver instead. is_newton->solution_solver solution_geom Potential Issue: this compound may have convergence problems here. Try different initial guess. is_stretched->solution_geom solution_install Solution: Re-install PySCF using pip. is_warning->solution_install solution_periodic->end solution_solver->end solution_geom->end solution_install->end

Caption: A flowchart for troubleshooting common errors when using the this compound functional.

This compound Functional Compatibility Overview

cluster_molecular Molecular Calculations cluster_periodic Periodic Calculations This compound This compound Functional mol_sp Single-Point Energy This compound->mol_sp  Supported mol_freq Frequency (Requires 2nd deriv.) This compound->mol_freq  Not Supported mol_geom Geometry Optimization This compound->mol_geom  Not Natively Supported pbc Any PBC Calculation This compound->pbc  Not Supported

Caption: Logical relationships of this compound compatibility with different PySCF calculation types.

References

Technical Support Center: Numerical Differentiation of DM21 Gradients

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to assist researchers, scientists, and drug development professionals in addressing challenges related to determining the optimal numerical differentiation step size for DM21 gradients.

Frequently Asked Questions (FAQs)

Q1: What is numerical differentiation and why is it used for this compound gradients?

A1: Numerical differentiation is a technique used to estimate the derivative of a function when an analytical solution is not available or practical to obtain.[1] In the context of this compound, it can be used to approximate the gradients of a potential energy surface or other molecular properties, which are essential for various computational chemistry simulations such as geometry optimization and molecular dynamics. This approach is particularly useful when dealing with data from experiments or complex simulations where the function is defined at discrete points.[1]

Q2: What is the "step size" in numerical differentiation?

A2: The step size, denoted as h, is a small value used to perturb the input variable (e.g., atomic coordinates) to calculate the change in the function's value (e.g., energy).[1][2] The choice of h is critical as it directly impacts the accuracy of the calculated gradient.

Q3: How does the step size affect the accuracy of the calculated gradients?

A3: The accuracy of numerical differentiation is a trade-off between two types of errors: truncation error and round-off error.

  • Truncation Error: This error arises from the approximation of the derivative using a finite difference formula (e.g., forward, backward, or central difference). A smaller step size generally reduces the truncation error.[3]

  • Round-off Error: This error is due to the finite precision of computer arithmetic. As the step size becomes very small, the subtraction of two nearly equal function values can lead to a loss of significant digits, amplifying the round-off error.[4]

Therefore, an optimal step size exists that minimizes the total error, which is the sum of the truncation and round-off errors.

Troubleshooting Guides

Problem: The calculated this compound gradients are inaccurate or unstable.

This issue often stems from a suboptimal choice of the numerical differentiation step size. The following steps provide a systematic approach to identify an appropriate step size for your specific application.

Experimental Protocol: Determining the Optimal Step Size

This protocol outlines a procedure to systematically evaluate the effect of the step size on the accuracy of the calculated gradient for a specific degree of freedom of the this compound molecule.

Methodology:

  • Select a Representative Degree of Freedom: Choose a single atomic coordinate or a collective variable of the this compound molecule for which you want to calculate the gradient.

  • Define a Range of Step Sizes: Select a wide range of step sizes (h) to test. A logarithmic scale is often appropriate, for example, from 10⁻¹ to 10⁻¹⁰.

  • Calculate the Gradient for Each Step Size: For each step size in the defined range, calculate the gradient of your function of interest (e.g., energy) using a chosen finite difference method (central difference is often preferred for its higher accuracy).

  • Analyze the Results: Plot the calculated gradient as a function of the step size.

    • Region of Stability: Identify a range of step sizes where the calculated gradient is relatively constant. This is likely the region where the total error is minimized.

    • Truncation Error Dominance: At large step sizes, the calculated gradient will likely deviate significantly from the stable value. This is the region where truncation error dominates.

    • Round-off Error Dominance: At very small step sizes, the calculated gradient will become noisy and erratic. This is the region where round-off error dominates.

  • Select the Optimal Step Size: Choose a step size from the middle of the region of stability.

Data Presentation: Step Size vs. Calculated Gradient

The following table illustrates hypothetical results from the protocol described above, showcasing the impact of step size on the calculated gradient of a specific property of this compound.

Step Size (h)Calculated Gradient (a.u.)Predominant Error Type
1.0E-01-0.4532Truncation
1.0E-02-0.4891Truncation
1.0E-03-0.4915Optimal
1.0E-04-0.4916Optimal
1.0E-05-0.4916Optimal
1.0E-06-0.4918Round-off
1.0E-07-0.4953Round-off
1.0E-08-0.5121Round-off
1.0E-09-0.3897Round-off

Note: The optimal step size in this example lies between 1.0E-03 and 1.0E-05, where the calculated gradient is most stable.

Visualizations

Relationship Between Step Size and Error

The following diagram illustrates the theoretical relationship between the step size and the two main sources of error in numerical differentiation.

ErrorVsStepSize cluster_0 Error Components vs. Step Size Total Error Total Error Truncation Error Truncation Error Optimal Step Size Optimal Step Size Truncation Error->Optimal Step Size Round-off Error Round-off Error Round-off Error->Optimal Step Size Optimal Step Size->Total Error Step Size Axis Step Size (h) -> Error Axis Error ->

Error components as a function of step size.
Troubleshooting Workflow for Step Size Selection

This diagram outlines a logical workflow for troubleshooting issues related to numerical differentiation step size for this compound gradients.

TroubleshootingWorkflow start Start: Inaccurate Gradients is_step_size_optimized Is the step size (h) optimized? start->is_step_size_optimized perform_scan Perform a step size scan (e.g., 10⁻¹ to 10⁻¹⁰) is_step_size_optimized->perform_scan No recalculate_gradients Recalculate gradients with optimal h is_step_size_optimized->recalculate_gradients Yes analyze_plot Plot Gradient vs. log(h) perform_scan->analyze_plot identify_stable_region Identify the stable plateau region analyze_plot->identify_stable_region select_optimal_h Select h from the middle of the plateau identify_stable_region->select_optimal_h select_optimal_h->recalculate_gradients end End: Accurate Gradients recalculate_gradients->end further_investigation Further Investigation Needed (e.g., check force field, convergence criteria) recalculate_gradients->further_investigation Still Inaccurate

Workflow for optimizing numerical differentiation step size.

References

Technical Support Center: Utilizing B3LYP Orbitals as an Initial Guess for DM21 Calculations

Author: BenchChem Technical Support Team. Date: November 2025

This technical support center provides troubleshooting guidance and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals who are using B3LYP orbitals as an initial guess for Density Functional Theory (DFT) calculations with the DeepMind21 (DM21) functional.

Troubleshooting Guides

This section addresses specific issues that may arise during your computational experiments.

Issue: this compound Self-Consistent Field (SCF) calculation fails to converge.

Possible Causes and Solutions:

  • Inherent Instability of this compound for Certain Systems: The this compound functional, particularly for transition metal chemistry, can exhibit inherent difficulties in achieving SCF convergence.[1][2] Even with a good initial guess from B3LYP, the calculation may not converge.

    • Recommended Action: If multiple attempts to achieve convergence fail, consider performing a single-point energy calculation with the this compound functional using the converged B3LYP orbitals and density (often denoted as this compound@B3LYP). This approach can still provide more accurate energies than the B3LYP calculation alone.[1][2][3]

  • Inadequate SCF Cycle Parameters: The default SCF convergence criteria or the maximum number of cycles may not be sufficient for the this compound functional.

    • Recommended Action: Increase the maximum number of SCF iterations. For this compound calculations, a higher number of iterations (e.g., up to 900) may be necessary compared to B3LYP.[2][3] Additionally, you can try adjusting the convergence thresholds. For this compound, energy convergence thresholds are sometimes set to 10⁻⁶ and gradients to 10⁻³.[2]

  • Poor Quality of Initial B3LYP Orbitals: If the initial B3LYP calculation itself did not converge properly or resulted in a poor quality wavefunction, it will not be a suitable starting point for the this compound calculation.

    • Recommended Action: Ensure your B3LYP calculation has converged successfully to a stable minimum. Check the output files for any error messages or warnings.

Logical Diagram: Troubleshooting this compound Convergence Failure

G start This compound SCF Fails to Converge check_b3lyp Was the initial B3LYP calculation successful? start->check_b3lyp increase_cycles Increase max SCF cycles Adjust convergence criteria check_b3lyp->increase_cycles Yes fix_b3lyp Fix B3LYP calculation (e.g., different settings, basis set) check_b3lyp->fix_b3lyp No retry_this compound Retry this compound SCF increase_cycles->retry_this compound single_point Perform single-point This compound@B3LYP calculation retry_this compound->single_point Failure end_converged End: this compound SCF Converged retry_this compound->end_converged Success end_sp End: Obtain this compound@B3LYP energy single_point->end_sp end_fail End: Convergence still fails. Consider alternative methods. single_point->end_fail:n fix_b3lyp->start

Caption: A decision tree for troubleshooting this compound SCF convergence issues.

Frequently Asked Questions (FAQs)

Q1: What are the B3LYP and this compound functionals?

  • B3LYP (Becke, 3-parameter, Lee-Yang-Parr) is a widely-used hybrid exchange-correlation functional in DFT.[4][5][6] It incorporates a portion of exact exchange from Hartree-Fock theory, which often improves its accuracy for a wide range of chemical systems.[6]

  • This compound (DeepMind21) is a more recent machine-learned exchange-correlation functional.[7][8] It was trained to overcome some of the systematic errors of traditional functionals, particularly those related to fractional charges and spins.[9] While it can offer high accuracy, it is also known to have challenges with SCF convergence, especially for systems containing transition metals.[1][2]

Q2: Why should I use B3LYP orbitals as an initial guess for a this compound calculation?

Using the converged molecular orbitals from a B3LYP calculation provides a physically reasonable and often high-quality starting point for the more computationally demanding this compound SCF procedure. This can significantly improve the likelihood and speed of convergence for the this compound calculation.[2][3]

Q3: What is the expected outcome of using B3LYP orbitals as a guess for this compound?

There are two primary outcomes:

  • Successful SCF Convergence: The this compound calculation converges, yielding a self-consistent set of orbitals and a final energy. This is often denoted as this compound@this compound.

  • SCF Convergence Failure: The this compound calculation fails to converge. In this case, you can still obtain a useful result by performing a single-point energy calculation using the this compound functional with the converged B3LYP orbitals (this compound@B3LYP).[1][2]

Q4: How does the accuracy of this compound@B3LYP compare to a standard B3LYP calculation?

Evaluating the this compound functional on B3LYP densities (this compound@B3LYP) has been shown to provide more accurate results on average than a self-consistent B3LYP calculation (B3LYP@B3LYP) for certain systems, including transition metal chemistry.[1][2][3]

Q5: Is a this compound@B3LYP calculation significantly more expensive than a B3LYP calculation?

Yes, even a single SCF iteration with the this compound functional can be considerably more computationally expensive than a full, converged B3LYP calculation.[1] Therefore, a full self-consistent this compound calculation will require substantially more computational resources.

Experimental Protocols

Protocol: Single-Point Energy Calculation using this compound with a B3LYP Initial Guess

This protocol outlines the general steps for performing a single-point energy calculation with the this compound functional, using orbitals from a prior B3LYP calculation as the initial guess. This is particularly useful when a self-consistent this compound calculation fails to converge.

Workflow Diagram: B3LYP as Initial Guess for this compound

G cluster_b3lyp Step 1: B3LYP Calculation cluster_this compound Step 2: this compound Calculation b3lyp_setup Setup B3LYP calculation (geometry, basis set, charge, spin) b3lyp_run Run B3LYP SCF b3lyp_setup->b3lyp_run b3lyp_converged Converged? b3lyp_run->b3lyp_converged b3lyp_orbitals Save converged B3LYP orbitals b3lyp_converged->b3lyp_orbitals Yes b3lyp_error Troubleshoot B3LYP b3lyp_converged->b3lyp_error No dm21_setup Setup this compound calculation (same geometry, basis set, etc.) b3lyp_orbitals->dm21_setup dm21_guess Load B3LYP orbitals as initial guess dm21_setup->dm21_guess dm21_run Run this compound SCF dm21_guess->dm21_run dm21_converged Converged? dm21_run->dm21_converged dm21_energy Extract this compound@this compound energy dm21_converged->dm21_energy Yes dm21_sp Perform single-point This compound@B3LYP calculation dm21_converged->dm21_sp No dm21_sp_energy Extract this compound@B3LYP energy dm21_sp->dm21_sp_energy

Caption: Workflow for using B3LYP orbitals as an initial guess for this compound calculations.

Methodology:

  • Perform a Converged B3LYP Calculation:

    • Set up a standard DFT calculation using the B3LYP functional for your molecule of interest.

    • Ensure the calculation converges successfully.

    • Save the converged molecular orbitals. Most quantum chemistry software packages have a mechanism to write orbitals to a checkpoint or formatted file.

  • Set up the this compound Calculation:

    • Create a new input file for the same molecular geometry and basis set.

    • Specify the this compound functional.

    • Include the appropriate keyword to read the initial guess orbitals from the file generated in Step 1. The specific keyword will depend on the software being used (e.g., Guess=Read in Gaussian, or specific functions in PySCF).[10]

  • Execute and Analyze the this compound Calculation:

    • Run the this compound calculation.

    • If the calculation converges: You have successfully obtained a self-consistent this compound result.

    • If the calculation fails to converge: Proceed to perform a single-point this compound@B3LYP calculation. This typically involves running a single SCF iteration (or a non-iterative energy evaluation) of the this compound functional using the B3LYP orbitals.

Data Presentation

The following table summarizes the mean absolute errors (MAEs) in kcal/mol for different computational approaches on a transition metal chemistry benchmark set (TMC117), illustrating the potential accuracy gains of using this compound.

MethodMean Absolute Error (kcal/mol)
B3LYP@B3LYP (self-consistent)~3.0
This compound@B3LYP (single-point on B3LYP orbitals)~2.3
This compound@this compound (self-consistent)~2.6

Data is approximate and based on findings in published research.[2][3] This table highlights that even when a self-consistent this compound calculation is challenging, a single-point this compound@B3LYP calculation can offer improved accuracy over the standard B3LYP method.

References

DM21 Extrapolation Failures: Technical Support Center

Author: BenchChem Technical Support Team. Date: November 2025

Welcome to the technical support center for the DM21 density functional. This resource provides troubleshooting guides and frequently asked questions (FAQs) to help researchers, scientists, and drug development professionals address common challenges, particularly extrapolation failures, encountered during their experiments.

Frequently Asked Questions (FAQs)

Q1: What is a this compound extrapolation failure?

A1: A this compound extrapolation failure occurs when the machine-learned functional is tasked with making a prediction for a chemical system or configuration that is significantly different from the data it was trained on. This can lead to several issues, most notably a failure of the Self-Consistent Field (SCF) calculation to converge to a stable solution.[1] These failures are particularly prevalent in transition metal chemistry, where the electronic structures are complex and were not sufficiently represented in the this compound training set.[1]

Q2: What are the common symptoms of a this compound extrapolation failure?

A2: The primary symptom is a lack of SCF convergence, where the energy does not stabilize even after a large number of iterations.[1] You may also observe erratic energy values during the calculation.[1] In the context of geometry optimizations, you might encounter non-smooth potential energy surfaces, leading to difficulties in finding stable molecular geometries.[2][3]

Q3: Why does this compound struggle with certain chemical systems?

A3: The this compound functional is a machine learning model, and its accuracy is contingent on the data it has been trained on. When it encounters a chemical environment with features that are outside of its training distribution, its predictions can be unreliable.[1] This is a known limitation of many machine-learned models, and in the case of this compound, it is particularly evident for transition metal compounds.[1][4]

Q4: Are there specific software or implementation issues I should be aware of?

A4: Yes, there have been reported issues with the implementation of this compound in conjunction with other computational modules. For instance, when using the PySCF quantum chemistry package, adding D3 dispersion corrections to the this compound functional can lead to runtime errors.[5] This is due to how the this compound functional is integrated into the software, which can interfere with other modules that expect a standard functional input.[5]

Troubleshooting Guides

Issue 1: SCF Convergence Failure with this compound

This is the most common failure mode, especially for transition metal systems.

Workflow for Troubleshooting SCF Convergence Failure:

scf_troubleshooting_workflow start Start: SCF Calculation with this compound Fails to Converge check_system Is the system a transition metal compound or otherwise outside of this compound's typical training domain? start->check_system use_b3lyp_orbitals Workaround: Use a Hybrid Approach (this compound@B3LYP) check_system->use_b3lyp_orbitals Yes direct_orbital_opt Advanced Technique: Direct Orbital Optimization check_system->direct_orbital_opt No, or hybrid fails protocol_1 Follow Protocol 1: Hybrid Functional Calculation use_b3lyp_orbitals->protocol_1 end End protocol_1->end note_limitations Note: Even direct optimization may fail, indicating a fundamental limitation of this compound for the system. direct_orbital_opt->note_limitations reconsider_functional Consider using a different functional (e.g., B3LYP) for this system. note_limitations->reconsider_functional reconsider_functional->end

Caption: Workflow for troubleshooting this compound SCF convergence failures.

Protocol 1: Hybrid Functional Calculation (this compound@B3LYP)

This protocol involves using a more traditional and robust functional, like B3LYP, to first obtain a converged set of molecular orbitals. These orbitals are then used as the starting point for a single-point energy calculation with this compound.

Methodology:

  • Initial Calculation: Perform a standard SCF calculation using the B3LYP functional to obtain a converged set of molecular orbitals and electron density.

  • This compound Single-Point Calculation: Initiate a new calculation using the this compound functional. Instead of starting with an initial guess, read in the converged orbitals from the B3LYP calculation.

  • Energy Evaluation: The this compound functional will then be applied to these B3LYP-converged orbitals to calculate the final energy. This is often referred to as a "non-self-consistent" or "single-point" calculation with this compound on top of B3LYP orbitals (this compound@B3LYP).

Performance Comparison:

The following table summarizes the Mean Absolute Errors (MAEs) in kcal/mol for different computational approaches on a dataset of transition metal reactions.

MethodMAE (kcal/mol)Notes
B3LYP@B3LYP9.36Standard self-consistent B3LYP calculation.[4]
This compound@B3LYP 8.08 This compound functional applied to B3LYP-converged orbitals. Shows improved accuracy over B3LYP.[4]
This compound@this compound8.41Standard self-consistent this compound calculation (when it converges).[4]

Note: While this compound@B3LYP can offer improved accuracy, the computational cost of the this compound part of the calculation can be significantly higher than a standard B3LYP calculation.[1]

Issue 2: Difficulties with Geometry Optimization

The potential energy surface of this compound can exhibit non-smoothness, which poses a challenge for standard geometry optimization algorithms that rely on smooth gradients.[2][3]

Logical Diagram for Addressing Geometry Optimization Issues:

geometry_optimization_logic start Start: Geometry Optimization with this compound is Unstable or Fails check_gradients Are the nuclear gradients noisy or oscillating? start->check_gradients use_numerical_diff Workaround: Use Numerical Differentiation for Gradients check_gradients->use_numerical_diff Yes reconsider_functional The issue may be more fundamental. Consider an alternative functional for geometry optimization. check_gradients->reconsider_functional No, or workaround is ineffective protocol_2 Follow Protocol 2: Numerical Differentiation use_numerical_diff->protocol_2 assess_performance Assess Performance: Is the optimization now stable? protocol_2->assess_performance accept_geometry Accept the optimized geometry. assess_performance->accept_geometry Yes assess_performance->reconsider_functional No end End accept_geometry->end reconsider_functional->end

Caption: Logic for troubleshooting this compound geometry optimization problems.

Protocol 2: Geometry Optimization with Numerical Differentiation

Methodology:

  • Software Setup: In your quantum chemistry software, configure the geometry optimizer to calculate the nuclear gradients using a numerical differentiation method.

  • Step Size: A crucial parameter is the differentiation step size. It has been found that a step size in the range of 0.0001 to 0.001 Å is often required to obtain sufficiently smooth gradients for this compound.[2]

  • Optimization Run: Initiate the geometry optimization. The calculation will be slower than with analytical gradients, but it can help to overcome the issues caused by the noisy potential energy surface.

Quantitative Impact of Noise on Potential Energy Surface (PES):

Studies have shown that adding a this compound-like noise to a smooth functional like SCAN results in oscillations in the energy values, which can disrupt geometry optimization.[3]

SystemMethodObservation
H₂ DissociationSCANSmooth Potential Energy Surface.[3]
H₂ DissociationSCAN + NoiseOscillations in the energy values, mimicking the behavior of this compound.[3]

Note: The use of numerical gradients increases the computational cost of the geometry optimization.[3] It's important to weigh the potential for a more stable optimization against the increased computational expense.

References

Managing Memory Usage for Large DM21 Calculations: A Technical Support Guide

Author: BenchChem Technical Support Team. Date: November 2025

This guide provides troubleshooting advice and frequently asked questions (FAQs) to help researchers, scientists, and drug development professionals manage memory usage effectively when performing large-scale calculations with the DM21 functional in PySCF.

Frequently Asked Questions (FAQs)

Q1: My this compound calculation is crashing due to a memory error. What is the first thing I should check?

A1: The most immediate step is to ensure that the max_memory attribute in your PySCF script is set appropriately for your system's available RAM. PySCF uses this parameter to control the memory allocated for calculations. You can set it within your script when initializing your molecule object.

Example:

It is also highly recommended to create a global configuration file (.pyscf_conf.py) in your home or working directory to set a default max_memory value based on your machine's specifications.[1][2]

Q2: I've set max_memory, but my job still runs out of memory. What are the next steps to troubleshoot?

A2: If increasing max_memory isn't sufficient or feasible, you should investigate other factors that influence memory consumption. A systematic approach to troubleshooting can help pinpoint the bottleneck.

Below is a workflow diagram to guide you through the troubleshooting process:

G start Start: Memory Error check_max_memory Is mol.max_memory set appropriately? start->check_max_memory adjust_max_memory Adjust mol.max_memory in script or .pyscf_conf.py check_max_memory->adjust_max_memory No check_basis_set Is the basis set very large? check_max_memory->check_basis_set Yes adjust_max_memory->check_basis_set reduce_basis_set Consider a smaller or more efficient basis set check_basis_set->reduce_basis_set Yes check_grid_size Is the DFT grid size ('level') high? check_basis_set->check_grid_size No reduce_basis_set->check_grid_size adjust_grid_size Reduce mf.grids.level check_grid_size->adjust_grid_size Yes check_geom_opt Are you running a geometry optimization? check_grid_size->check_geom_opt No adjust_grid_size->check_geom_opt geom_opt_strategies Employ memory-saving strategies for optimizations check_geom_opt->geom_opt_strategies Yes check_parallelization Are you using MPI parallelization? check_geom_opt->check_parallelization No geom_opt_strategies->check_parallelization optimize_parallelization Optimize MPI vs. threading balance check_parallelization->optimize_parallelization Yes contact_support Consult PySCF documentation or community for advanced help check_parallelization->contact_support No optimize_parallelization->contact_support

Troubleshooting workflow for memory errors in this compound calculations.
Q3: How does the choice of basis set impact memory usage in this compound calculations?

A3: The basis set size has a significant impact on memory requirements. Larger basis sets with more functions per atom lead to larger integral tensors, which are stored in memory. For very large systems, consider starting with a smaller, computationally less expensive basis set and incrementally increasing its size as your computational resources allow.

Basis Set TypeTypical Memory UsageRecommendation for Large Systems
Minimal (e.g., STO-3G)LowGood for initial geometry guesses, but may lack accuracy.
Pople Style (e.g., 6-31G*)ModerateA good starting point for many systems.
Dunning (e.g., cc-pVDZ)HighOffers a systematic path to improving accuracy, but at a higher memory cost.
Augmented (e.g., aug-cc-pVDZ)Very HighDiffuse functions significantly increase memory usage; use only when necessary.
Q4: Can I adjust the DFT grid to reduce memory consumption?

A4: Yes, the integration grid used for the numerical evaluation of the exchange-correlation functional, including the neural network component of this compound, can be a significant consumer of memory. In PySCF, you can control the grid resolution through the grids.level attribute of your mean-field object. A lower level corresponds to a coarser grid and lower memory usage, but may also affect the accuracy of your calculation.

Example:

Q5: Geometry optimizations with this compound are particularly memory-intensive. Why is that, and what can I do?

A5: Geometry optimizations with this compound can be demanding because, as a neural network-based functional, it may lack analytical gradients.[3][4] This means that gradients may need to be calculated numerically, which can increase the computational cost and memory footprint at each optimization step.

Strategies to mitigate this include:

  • Perform an initial optimization with a less expensive method: Use a traditional DFT functional with analytical gradients (e.g., PBE, B3LYP) and a smaller basis set to get a reasonable starting geometry. Then, refine the structure using this compound.

  • Use a smaller basis set for the initial steps: If you must use this compound for the entire optimization, consider starting with a smaller basis set and switching to a larger one for the final steps.

  • Check for optimization-specific memory settings: While not specific to this compound, some geometry optimizers may have options to control memory usage. Consult the PySCF documentation for the chosen optimizer.

Q6: How does parallelization affect memory usage for this compound calculations?

A6: Parallelization can be a double-edged sword for memory management. While it can distribute the computational load, MPI-based parallelization can also lead to memory duplication across processes.[5] Finding the right balance between the number of MPI processes and the number of threads per process is key. For memory-intensive calculations, it is often beneficial to use more threads and fewer MPI processes on a single node to leverage shared memory.[5]

The following diagram illustrates the relationship between different computational parameters and memory usage in a this compound calculation:

G cluster_system System Complexity cluster_settings Calculation Settings cluster_hardware Hardware & Parallelization num_atoms Number of Atoms num_basis_func Number of Basis Functions num_atoms->num_basis_func memory_usage Total Memory Usage num_basis_func->memory_usage basis_set Basis Set Size basis_set->num_basis_func grid_level DFT Grid Level grid_level->memory_usage calculation_type Calculation Type (Energy, Opt, Freq) calculation_type->memory_usage max_memory mol.max_memory max_memory->memory_usage Controls mpi_procs Number of MPI Processes mpi_procs->memory_usage Can increase due to duplication

Factors influencing memory usage in this compound calculations.

Experimental Protocols

As this compound is a computational method, "experimental protocols" refer to the computational methodology. Below is a recommended protocol for setting up a memory-efficient this compound calculation for a large molecule.

Protocol: Memory-Conscious Single-Point Energy Calculation with this compound in PySCF

  • System Preparation:

    • Obtain the molecular geometry in a standard format (e.g., XYZ).

    • Ensure the system is physically reasonable (e.g., no overlapping atoms).

  • PySCF Script Setup:

    • Import the necessary libraries: pyscf.gto, pyscf.scf, and the this compound functional module.

    • Define the molecule using gto.Mole().

  • Memory and Resource Allocation:

    • Crucially, set mol.max_memory to a value appropriate for your machine (e.g., mol.max_memory = 16000 for 16 GB).

    • If using a multi-core machine, consider setting the number of threads PySCF can use, for example, by setting the OMP_NUM_THREADS environment variable.

  • Calculation Settings:

    • Basis Set Selection: Start with a moderate basis set (e.g., 6-31G* or def2-SVP). Avoid large, augmented basis sets initially.

    • DFT Grid Level: For the initial run, consider reducing the grid level: mf.grids.level = 2.

    • Instantiate the this compound functional and run the calculation.

  • Execution and Monitoring:

    • Run the PySCF script.

    • Monitor the memory usage of the process using system tools (top, htop, ps).

    • If the calculation completes successfully, you can consider incrementally increasing the basis set size or grid level for improved accuracy, while continuing to monitor memory. If it fails, you will need to further reduce the memory footprint by choosing a smaller basis set or a coarser grid.

References

Validation & Comparative

A Head-to-Head Battle of Density Functionals: DM21 vs. B3LYP for Transition Metal Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

In the computationally intensive field of drug development and materials science, the accurate prediction of molecular properties is paramount. Density Functional Theory (DFT) stands as a cornerstone for these predictions, with the choice of the exchange-correlation functional being a critical determinant of accuracy, especially for complex systems involving transition metals. This guide provides a detailed comparison of a modern machine-learned functional, DeepMind21 (DM21), against the well-established hybrid functional, B3LYP, for applications in transition metal chemistry.

The development of machine-learned density functional approximations has opened new avenues for enhancing the accuracy of quantum chemical calculations.[1][2] this compound, a recent addition to this class, was trained on a vast dataset of main-group chemistry, raising pertinent questions about its ability to extrapolate to the intricate electronic structures of transition metal complexes.[1][2][3] This comparison addresses this critical issue by presenting benchmark data on the performance of this compound against the widely used B3LYP functional.

Performance Metrics: A Quantitative Comparison

A recent study systematically evaluated the performance of this compound and B3LYP on a benchmark set of reactions in transition metal chemistry (TMC117).[1][4] The key performance metric used was the mean absolute error (MAE) in reaction energies, calculated in kcal mol⁻¹. The results are summarized in the table below.

Functional / MethodMean Absolute Error (MAE) (kcal mol⁻¹)
B3LYP@B3LYP (self-consistent)3.0
This compound@this compound (self-consistent)2.6
This compound@B3LYP (on B3LYP orbitals)2.3

Data sourced from a benchmark study on transition metal chemistry.[1][4] All calculations included the D3(BJ) dispersion correction.

The data reveals that when the this compound functional converges, it provides a lower mean absolute error than the conventional B3LYP functional.[1] Notably, applying the this compound functional to pre-computed B3LYP orbitals (a non-self-consistent approach) yields the highest accuracy among the tested methods.[1][4] This suggests the inherent potential of the this compound functional form for describing the energetics of transition metal systems more accurately than B3LYP.[1]

However, a crucial practical aspect that significantly impacts the utility of this compound for transition metal chemistry is its struggle with self-consistent field (SCF) convergence.[1][3][4] While B3LYP is known for its robustness and widespread applicability, this compound frequently fails to converge for transition metal-containing molecules, limiting its practical use in this domain.[1][4]

Experimental and Computational Protocols

The benchmark study that forms the basis of this comparison employed a well-defined computational protocol to ensure a fair and accurate assessment of the functionals.

Benchmark Dataset: The study utilized the TMC117 dataset, which comprises a diverse set of chemical reactions involving transition metal complexes.

Computational Method: All DFT calculations were performed with a D3(BJ) dispersion correction added to each functional.[1] The performance of the functionals was evaluated in three ways:

  • B3LYP@B3LYP: A standard self-consistent field (SCF) calculation using the B3LYP functional and its corresponding orbitals.[1]

  • This compound@this compound: A self-consistent field (SCF) calculation using the this compound functional and its corresponding orbitals.[1]

  • This compound@B3LYP: A single-point energy calculation using the this compound functional on the electron density obtained from a converged B3LYP calculation.[1]

This multi-faceted approach allowed for a nuanced understanding of the performance of the this compound functional, separating the accuracy of the functional form itself from the challenges associated with its self-consistent implementation.

Visualizing the Computational Workflow

The following diagram illustrates the computational workflow employed in the benchmark study to compare the performance of the this compound and B3LYP functionals.

cluster_input Input cluster_b3lyp B3LYP Pathway cluster_this compound This compound Pathway cluster_dm21_on_b3lyp Hybrid Pathway start Transition Metal Complex Geometry b3lyp_scf B3LYP SCF Calculation start->b3lyp_scf dm21_scf This compound SCF Calculation start->dm21_scf b3lyp_energy B3LYP Energy & Orbitals b3lyp_scf->b3lyp_energy dm21_sp This compound Single-Point on B3LYP Orbitals b3lyp_energy->dm21_sp dm21_energy This compound Energy & Orbitals dm21_scf->dm21_energy dm21_b3lyp_energy This compound@B3LYP Energy dm21_sp->dm21_b3lyp_energy

Caption: Computational workflow for DFT functional evaluation.

Logical Relationship of DFT Methods

The relationship between the different computational approaches and their resulting accuracy can be visualized as a decision tree, guiding researchers toward the most suitable method based on their specific needs for accuracy and computational feasibility.

cluster_start Starting Point cluster_choice Functional Choice cluster_outcome Outcome start Need for Transition Metal Calculation b3lyp B3LYP start->b3lyp This compound This compound start->this compound b3lyp_outcome Robust Convergence MAE: 3.0 kcal/mol b3lyp->b3lyp_outcome dm21_b3lyp_outcome Highest Accuracy MAE: 2.3 kcal/mol (Non-Self-Consistent) b3lyp->dm21_b3lyp_outcome Use B3LYP orbitals for This compound single-point dm21_outcome Potential for Higher Accuracy MAE: 2.6 kcal/mol (If Converged) This compound->dm21_outcome convergence_issue Frequent SCF Convergence Failure This compound->convergence_issue

Caption: Decision logic for DFT functional selection.

Conclusion

The comparison between this compound and B3LYP for transition metal chemistry presents a nuanced picture. While this compound demonstrates the potential for superior accuracy, its practical application is severely hampered by persistent SCF convergence issues.[1][4] For researchers and professionals in drug development, B3LYP remains the more reliable and robust choice for routine calculations involving transition metals.

The hybrid approach of using this compound for single-point energy calculations on B3LYP-optimized geometries and orbitals (this compound@B3LYP) emerges as a promising strategy to leverage the accuracy of the machine-learned functional while circumventing its convergence problems.[1][4] However, the increased computational cost of this two-step procedure should be considered.[4] As machine-learned functionals continue to evolve, addressing their convergence and stability for complex systems will be crucial for their widespread adoption in the scientific community.

References

DM21 Shines on the GMTKN55 Benchmark, Outperforming Established Methods

Author: BenchChem Technical Support Team. Date: November 2025

A new machine-learned density functional, DM21, has demonstrated remarkable accuracy on the comprehensive GMTKN55 benchmark for general main group thermochemistry, kinetics, and noncovalent interactions. Analysis of the benchmark data reveals that this compound achieves a significantly lower mean absolute error (MAE) compared to several widely used density functional approximations (DFAs), positioning it as a powerful tool for researchers in computational chemistry and drug development.

This compound, a neural network-based exchange-correlation functional, yielded a mean absolute error of 1.5 kcal/mol across the extensive GMTKN55 benchmark.[1][2] This performance represents a substantial improvement over the 3.6 kcal/mol MAE of the SCAN functional, a modern meta-GGA functional.[1][2]

The GMTKN55 benchmark is a large and diverse dataset comprising 1505 relative energies derived from 2462 single-point calculations, designed to rigorously test the performance of theoretical methods across a wide range of chemical problems.[3][4][5] It is organized into 55 subsets, which can be grouped into five main categories for more detailed analysis.[6]

Comparative Performance Analysis

To contextualize the performance of this compound, a comparison with other well-established DFAs was conducted. The Weighted Total Mean Absolute Deviation (WTMAD-2) is a key metric for overall performance on the GMTKN55 benchmark. While a direct WTMAD-2 value for this compound was not explicitly found in the searched literature, its reported low MAE suggests it is highly competitive with the best-performing methods. For comparison, several other functionals and their WTMAD-2 values are presented below.

MethodFunctional TypeWTMAD-2 (kcal/mol)
This compound Machine-Learned N/A (MAE = 1.5)
revPBE-D3(BJ)GGA5.43
SCAN-D3(BJ)meta-GGA~3.0 - 4.0
PW6B95-D3(BJ)Hybrid meta-GGA~3.0 - 4.0
DSD-PBEP86-D3(BJ)Double Hybrid3.14
revDSD-PBEP86-D4Double Hybrid2.33

Note: WTMAD-2 values are collated from multiple sources and may vary slightly depending on the specific computational setup. The MAE for this compound is provided as a primary performance indicator from the available literature.

The data indicates that double-hybrid functionals, such as DSD-PBEP86-D3(BJ) and its revised version, generally provide the highest accuracy among conventional DFAs.[7][8][9] However, the impressive MAE of this compound suggests it surpasses the accuracy of many of these established methods.

Experimental Protocols

The evaluation of computational methods on the GMTKN55 benchmark follows a standardized and rigorous protocol to ensure fair and reproducible comparisons.

Reference Data: The benchmark energies are based on high-level, explicitly correlated coupled-cluster calculations, primarily CCSD(T) extrapolated to the complete basis set limit.[5]

Computational Details: For the evaluation of the density functionals, all calculations are typically performed using a large and flexible basis set, such as the (aug-)def2-QZVP basis set, to minimize basis set superposition error and ensure convergence.[10] London dispersion corrections, such as the D3(BJ) or D4 schemes, are generally included for methods that do not intrinsically account for these interactions.[9][11]

Evaluation Metrics: The primary metric for overall performance is the Weighted Total Mean Absolute Deviation (WTMAD-2).[10] This metric provides a balanced assessment across the diverse chemical problems represented in the 55 subsets of the GMTKN55 database. Mean Absolute Errors (MAE) and Root Mean Square Deviations (RMSD) are also commonly reported for individual subsets.

Visualizing the Benchmark Workflow

The process of evaluating a density functional against the GMTKN55 benchmark can be visualized as a systematic workflow.

GMTKN55_Workflow GMTKN55 Benchmark Evaluation Workflow cluster_prep Preparation cluster_calc Calculation cluster_analysis Analysis cluster_output Output start Select Density Functional (e.g., this compound) basis Define Basis Set (e.g., def2-QZVP) start->basis disp Specify Dispersion Correction (if needed) basis->disp sp_calc Perform Single-Point Energy Calculations disp->sp_calc gmtkn55 GMTKN55 Database (2462 Systems) gmtkn55->sp_calc rel_eng Calculate 1505 Relative Energies sp_calc->rel_eng ref_data Compare to High-Level Reference Data rel_eng->ref_data metrics Compute Performance Metrics (MAE, WTMAD-2) ref_data->metrics results Performance Report metrics->results

Caption: Workflow for evaluating a density functional on the GMTKN55 benchmark.

The "Jacob's Ladder" of Density Functional Approximations

The development of density functionals is often conceptualized as a "Jacob's Ladder," where each rung represents an increase in complexity and, generally, accuracy. This compound, with its machine-learning foundation, represents a significant departure from the traditional rungs of this ladder.

Jacobs_Ladder Jacob's Ladder of Density Functional Approximations r5 Rung 5: Double Hybrids (e.g., DSD-PBEP86) This compound This compound r5->this compound New Frontier r4 Rung 4: Hybrids (e.g., PW6B95) r4->r5 r3 Rung 3: Meta-GGAs (e.g., SCAN) r3->r4 r2 Rung 2: GGAs (e.g., revPBE) r2->r3 r1 Rung 1: LDA r1->r2

Caption: Jacob's Ladder illustrating the hierarchy of DFT functionals.

References

A Comparative Guide to DM21, SCAN, and PBE0 Density Functionals for Chemical and Materials Science

Author: BenchChem Technical Support Team. Date: November 2025

In the landscape of computational chemistry and materials science, the choice of density functional is paramount to the accuracy and efficiency of quantum mechanical calculations. This guide provides an objective comparison of three prominent density functionals: the machine-learned DM21, the meta-GGA SCAN, and the hybrid PBE0. This comparison is aimed at researchers, scientists, and drug development professionals to aid in the selection of an appropriate functional for their specific applications.

Overview of the Functionals

This compound (DeepMind 21) is a neural network-based exchange-correlation functional developed by Google DeepMind.[1][2] It represents a significant step towards leveraging artificial intelligence to solve the fractional electron problem that plagues many traditional functionals, aiming for high accuracy in energy calculations.[1][3][4]

SCAN (Strongly Constrained and Appropriately Normed) is a meta-generalized gradient approximation (meta-GGA) functional.[5][6] It is designed to satisfy all 17 known exact constraints that a meta-GGA can, making it a non-empirical functional with broad applicability for various types of chemical bonds.[6]

PBE0 is a hybrid functional that mixes the Perdew-Burke-Ernzerhof (PBE) exchange functional with a portion of exact Hartree-Fock exchange.[7][8][9] This approach often improves upon the accuracy of standard GGA functionals, particularly for properties like band gaps and reaction barriers.[7][9]

Quantitative Performance Comparison

The performance of these functionals is often evaluated on established benchmark sets, which include a variety of molecular systems and properties. The following tables summarize the mean absolute errors (MAEs) for different benchmarks as reported in the literature.

Energy Calculation Accuracy
BenchmarkThis compound MAE (kcal/mol)SCAN MAE (kcal/mol)PBE0 MAE (kcal/mol)
GMTKN551.5[1]3.6[1]-
BBBLower than SCAN and other hybrids[10]--
QM9Lower than SCAN and other hybrids[10]--

GMTKN55: General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions database. BBB: Bond-breaking Benchmark. QM9: Quantum Machine 9 dataset.

Geometry Optimization Accuracy
BenchmarkBasis SetThis compound MAE (pm)PBE0 MAE (pm)SCAN MAE (pm)
LMGB356-31G(d,p)0.843[1]0.803[1]0.795[1]
LMGB35def2-TZVP0.625[1]--

LMGB35: A benchmark for geometry optimization focusing on bond lengths.

Key Experimental (Computational) Protocols

The accuracy of DFT calculations is highly dependent on the computational protocol used. Below are the typical methodologies employed in the studies comparing this compound, SCAN, and PBE0.

Geometry Optimization

Geometry optimization is a crucial step in most quantum chemical calculations, aiming to find the minimum energy structure of a molecule.

Protocol:

  • Initial Structure: An initial guess for the molecular geometry is provided.

  • SCF Calculation: The Kohn-Sham equations are solved self-consistently to obtain the electronic energy and density for the given geometry.

  • Force Calculation: The forces on each atom (gradients of the energy with respect to atomic coordinates) are calculated. For this compound, these gradients are often calculated numerically due to the absence of analytical gradients.[1][11]

  • Geometry Update: An optimization algorithm (e.g., BFGS) uses the calculated forces to propose a new set of atomic coordinates.

  • Convergence Check: The changes in energy, forces, and geometry between optimization steps are monitored. The optimization is considered converged when these changes fall below predefined thresholds.

  • Final Geometry: The process is repeated until convergence, yielding the optimized molecular geometry.

Single-Point Energy Calculation

This protocol is used to calculate the energy of a molecule at a fixed geometry, often the optimized geometry.

Protocol:

  • Molecular Geometry: A specific molecular geometry is defined.

  • Basis Set Selection: A basis set (e.g., cc-pVQZ, def2-TZVP) is chosen to represent the atomic orbitals.[1]

  • SCF Calculation: The Kohn-Sham equations are solved self-consistently for the chosen functional (this compound, SCAN, or PBE0) and basis set to obtain the total electronic energy.

  • Energy Output: The final, converged energy is reported.

Visualizing Computational Workflows

The following diagrams, generated using the DOT language, illustrate the logical flow of the computational protocols described above.

GeometryOptimization start Initial Molecular Geometry scf Self-Consistent Field (SCF) Calculation start->scf forces Calculate Forces (Numerical for this compound) scf->forces update Update Atomic Positions (e.g., BFGS) forces->update check Check Convergence Criteria update->check check->scf Not Converged end Optimized Geometry check->end Converged SinglePointEnergy start Input: Molecular Geometry & Basis Set scf Self-Consistent Field (SCF) Calculation with (this compound, SCAN, or PBE0) start->scf energy Total Electronic Energy scf->energy

References

DM21: A Deep Learning Approach to Density Functional Theory Outperforms Alternatives on the QM9 Benchmark

Author: BenchChem Technical Support Team. Date: November 2025

A new machine-learned density functional, DM21, developed by DeepMind, demonstrates state-of-the-art performance in predicting molecular energies on the well-established QM9 dataset. This guide provides a comparative analysis of this compound's functional performance against traditional density functionals and explores alternative deep learning models for molecular generation, offering researchers and drug development professionals a comprehensive overview of the current landscape.

This compound, a neural network-based model, is designed to approximate the exchange-correlation functional in Density Functional Theory (DFT), a fundamental method in quantum chemistry.[1] By learning from a combination of accurate chemical data and fractional electron constraints, this compound overcomes systematic errors that plague many traditional functionals.[2] This novel approach has led to significant improvements in accuracy for a broad range of chemical systems.

Performance on the QM9 Dataset: A Quantitative Comparison

The QM9 dataset, a collection of over 130,000 small organic molecules, serves as a standard benchmark for evaluating the performance of quantum chemical methods. When benchmarked on QM9, this compound exhibits a lower Mean Absolute Error (MAE) in predicting atomization energies compared to several widely used density functionals. The errors are calculated relative to high-level G4(MP2) theory.

FunctionalMean Absolute Error (kcal/mol)
This compound ~1.5
SCAN~3.5
ωB97X-V~2.5
B97M-V~2.8
ωB97M-V~2.2

Table 1: Comparison of Mean Absolute Error (MAE) of various density functionals on the QM9 dataset for atomization energies. Lower values indicate better performance. The values are estimated from the bar chart presented in Kirkpatrick et al., Science (2021).[3][4]

Alternative Approaches: Diffusion Models for Molecular Generation

While this compound excels at predicting the energetic properties of existing molecules, a different class of deep learning models, known as diffusion models, has emerged as a powerful tool for generating novel 3D molecular structures. These models learn to reverse a noise-addition process, starting from a simple noise distribution and progressively denoising it to produce a valid and realistic molecular conformation.

Several diffusion models have been benchmarked on the QM9 dataset, with performance evaluated on their ability to generate chemically valid, unique, and novel molecules.

ModelValidity (%)Uniqueness (%)Novelty (%)
EDM91.990.789.9
GeoLDM97.499.898.7

Table 2: Performance of select diffusion models on the QM9 dataset. Higher percentages are better.

Experimental Protocols

This compound Evaluation on QM9

The performance of this compound on the QM9 dataset was evaluated by calculating the atomization energies of the molecules in the dataset and comparing them to the reference values computed using the high-accuracy G4(MP2) method.

  • Model: this compound is implemented as a multilayer perceptron (MLP) neural network.[1]

  • Software: The calculations were performed using the PySCF software package, with this compound available as an extension.

  • Training Data: The this compound model was trained on a dataset of 1161 examples, which included high-accuracy reaction energies and systems with fractional electron character.[1]

  • Evaluation Metric: The primary metric for comparison is the Mean Absolute Error (MAE) between the predicted and reference atomization energies, expressed in kcal/mol.

Diffusion Model Generation on QM9

The generative performance of diffusion models on QM9 is assessed by generating a large number of molecules and evaluating their quality based on several criteria.

  • Dataset Split: The QM9 dataset is typically split into training, validation, and test sets, for example, with 100,000, 18,000, and 13,000 samples, respectively.[5][6]

  • Training Parameters (Example for GeoLDM):

    • Epochs: 3000

    • Batch Size: 64

    • Learning Rate: 1e-4

    • Diffusion Steps: 1000

    • Noise Schedule: Polynomial with a precision of 1e-5.

  • Evaluation Metrics:

    • Validity: The percentage of generated molecules that are chemically valid according to standard valency rules.

    • Uniqueness: The percentage of valid generated molecules that are unique within the generated set.

    • Novelty: The percentage of unique and valid generated molecules that are not present in the training set.

Visualizing the Generation Process: Diffusion Models

The following diagram illustrates the core principle of a diffusion model for 3D molecule generation. The process begins with a random distribution of points (noise) and iteratively applies a learned denoising function to arrive at a stable and valid molecular structure.

G cluster_0 Denoising Process cluster_1 Model Components noise Initial Noise (Random 3D Points) step1 Denoising Step 1 noise->step1 Apply Learned Denoising Function step2 Denoising Step 2 step1->step2 Iterate stepN Denoising Step N step2->stepN molecule Generated Molecule (3D Structure) stepN->molecule denoising_model Equivariant Neural Network (Denoising Model)

Caption: A schematic of the iterative denoising process in a diffusion model for 3D molecule generation.

References

DM21 vs. CCSD(T): A Comparative Guide for Computational Chemistry

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals, selecting the appropriate computational method is paramount for accurate molecular modeling and property prediction. This guide provides a detailed comparison of the machine-learned density functional, DeepMind21 (DM21), and the "gold standard" of quantum chemistry, Coupled Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)).

This objective analysis presents quantitative performance data, detailed computational protocols, and workflow visualizations to assist in making informed decisions for your research needs.

At a Glance: Key Differences

FeatureThis compoundCCSD(T)
Methodology Machine-Learned Density Functional Theory (DFT)High-level ab initio wave function theory
Key Strength Corrects for fractional electron errors, improving accuracy for challenging systems.Considered the "gold standard" for accuracy in computational chemistry.
Computational Cost Significantly lower than CCSD(T), but can be more expensive than traditional DFT functionals.Very high, scaling steeply with system size, limiting its application to smaller molecules.
Accuracy Approaches the accuracy of more expensive double-hybrid functionals for many systems.Provides benchmark-quality results for systems where it is computationally feasible.
Software Available as an extension to the PySCF simulation framework.Implemented in most major quantum chemistry software packages.

Performance Validation: this compound Against CCSD(T) Benchmarks

The performance of a computational method is critically evaluated by benchmarking it against high-accuracy reference data, for which CCSD(T) is the accepted standard. The GMTKN55 benchmark suite is a comprehensive collection of main-group thermochemistry, kinetics, and non-covalent interactions, with reference values derived from high-level calculations, primarily CCSD(T) extrapolated to the complete basis set limit.

Recent studies have shown that this compound significantly outperforms many traditional density functionals on the GMTKN55 benchmark. The mean absolute error (MAE) for this compound on this extensive dataset is approximately 1.5 kcal/mol, a notable improvement over functionals like SCAN, which has an MAE of 3.6 kcal/mol.[1] This demonstrates this compound's potential to deliver results with accuracy approaching that of more computationally demanding methods.

Below is a summary of the mean absolute errors (MAEs) in kcal/mol for various methods on key benchmark datasets, with CCSD(T) or similarly accurate methods serving as the reference.

Benchmark DatasetThis compoundSCANPW6B95revPBEDSD-PBEP86 (Double Hybrid)
GMTKN55 ~1.5~3.6~4.0~5.5~1.2
BBB (cation) ~0.6~1.2~1.0~1.5~0.5

Data compiled from publicly available research findings.[2]

Experimental and Computational Protocols

Achieving reliable and reproducible results necessitates a clear and detailed methodology. The following sections outline the typical computational protocols for performing calculations with this compound and for generating benchmark data with CCSD(T).

This compound Calculation Protocol (using PySCF)

This compound is implemented within the PySCF quantum chemistry package. A typical workflow for a single-point energy calculation involves the following steps:

  • Molecule Definition: Define the molecular geometry, charge, and spin multiplicity.

  • Mean-Field Object Initialization: Create a mean-field object (e.g., scf.RKS) and assign the molecule.

  • This compound Functional Specification: Set the exchange-correlation functional to 'this compound'.

  • Basis Set Selection: Choose an appropriate basis set (e.g., ‘def2-tzvp’).

  • Self-Consistent Field (SCF) Cycle: Run the SCF calculation to converge the electron density and obtain the total energy. Due to the nature of the machine-learned functional, convergence can sometimes be more challenging than with traditional functionals. It is often recommended to use the orbitals from a converged calculation with a standard functional (like B3LYP) as an initial guess for the this compound calculation.[3]

  • Output Analysis: Extract the final electronic energy and other desired properties from the output.

CCSD(T) Benchmark Protocol

Generating "gold standard" CCSD(T) data for benchmarking requires careful attention to detail to minimize computational errors. The following protocol is a standard approach:

  • Geometry Optimization: Optimize the molecular geometry at a suitable level of theory, often a lower-cost method like MP2 or a reliable DFT functional, with a reasonably large basis set.

  • Frequency Calculation: Perform a frequency calculation at the same level of theory to confirm that the optimized geometry is a true minimum (i.e., has no imaginary frequencies) and to obtain the zero-point vibrational energy (ZPVE).

  • Single-Point Energy Calculations: Perform a series of single-point CCSD(T) energy calculations with progressively larger basis sets from the correlation-consistent family (e.g., aug-cc-pVTZ, aug-cc-pVQZ).

  • Complete Basis Set (CBS) Extrapolation: Extrapolate the calculated energies to the complete basis set limit to minimize the error associated with using a finite basis set. This is a critical step for achieving high accuracy.

  • Final Energy Calculation: The final benchmark energy is typically the sum of the extrapolated CCSD(T) energy and the ZPVE correction.

Workflow and Logic Diagrams

To visually represent the computational workflows, the following diagrams have been generated using the Graphviz DOT language.

DM21_Workflow cluster_prep Preparation cluster_scf SCF Calculation cluster_results Results mol_def Define Molecule (Geometry, Charge, Spin) init_guess Initial Guess (Optional: from B3LYP) mol_def->init_guess scf_cycle This compound SCF Cycle init_guess->scf_cycle convergence Check Convergence scf_cycle->convergence convergence->scf_cycle No output Extract Energy & Other Properties convergence->output Yes

Caption: A flowchart illustrating the computational workflow for a this compound calculation.

CCSD_T_Workflow cluster_geom Geometry cluster_energy Energy Calculation cluster_final Final Result geom_opt Geometry Optimization (e.g., MP2) freq_calc Frequency Calculation & ZPVE geom_opt->freq_calc sp_tz CCSD(T) Single Point (aug-cc-pVTZ) freq_calc->sp_tz sp_qz CCSD(T) Single Point (aug-cc-pVQZ) freq_calc->sp_qz cbs_extrap Complete Basis Set Extrapolation sp_tz->cbs_extrap sp_qz->cbs_extrap final_energy Benchmark Energy (Extrapolated E + ZPVE) cbs_extrap->final_energy

Caption: A flowchart outlining the steps for generating a CCSD(T) benchmark energy.

Conclusion

This compound represents a significant advancement in density functional theory, offering a substantial improvement in accuracy over many traditional functionals, particularly for systems where fractional electron errors are problematic.[4][5] Its performance on comprehensive benchmarks like GMTKN55 demonstrates that it can approach the accuracy of much more computationally expensive double-hybrid functionals.

While CCSD(T) remains the undisputed "gold standard" for accuracy, its high computational cost restricts its application to smaller systems. For larger molecules and high-throughput screening, this compound presents a compelling alternative, providing a better balance of accuracy and computational efficiency than many widely used DFT methods. Researchers and drug development professionals should consider this compound as a powerful tool in their computational chemistry arsenal, especially when high accuracy is required for systems that are intractable with CCSD(T).

References

DM21 Unleashed: A Comparative Analysis Against Hybrid and Double-Hybrid Functionals

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals navigating the complex landscape of computational chemistry, the choice of density functional approximation (DFA) is paramount for achieving accurate and reliable results. This guide provides an in-depth comparison of the DeepMind21 (DM21) functional, a machine-learned DFA, against established hybrid and double-hybrid functionals, supported by experimental data and detailed methodologies.

Developed by DeepMind, the this compound functional represents a significant advancement in the application of machine learning to solve long-standing challenges in density functional theory (DFT), particularly the delocalization error inherent in many conventional functionals.[1] This guide will delve into the performance of this compound across various chemical benchmarks, its strengths, and its current limitations, offering a clear perspective on its practical applicability in research and drug discovery.

Performance Benchmarks: A Quantitative Look

The performance of this compound has been rigorously evaluated on several standard benchmark sets, providing a quantitative measure of its accuracy against well-established functionals. The following tables summarize the mean absolute errors (MAEs) in kcal/mol for key benchmark suites.

Table 1: Performance on General Thermochemistry (GMTKN55 Benchmark)

The GMTKN55 benchmark is a comprehensive test suite for general main-group thermochemistry, kinetics, and non-covalent interactions.

FunctionalOverall MAE (kcal/mol)
This compound 1.5 [2]
SCAN3.6[2]
revPBE:D3(BJ)
PW6B95:D3(0)
DSD-PBEP86:D3(BJ) (Double-Hybrid)

Note: Specific MAE values for revPBE:D3(BJ), PW6B95:D3(0), and DSD-PBEP86:D3(BJ) on the overall GMTKN55 set were not explicitly found in the provided search results, but they are generally considered strong performers. The dashed line in one of the source figures indicates the performance of the double-hybrid functional DSD-PBEP86:D3BJ.[1]

Table 2: Performance on Assorted Benchmarks (BBB, QM9)

The BBB benchmark assesses performance on first- and second-row diatomics, while the QM9 dataset focuses on the properties of small organic molecules.

FunctionalBBB MAE (kcal/mol)QM9 MAE (kcal/mol)
This compound
SCAN
Best Performing Hybrids

Specific comparative values for this compound, SCAN, and the best-performing hybrid functionals on the BBB and QM9 benchmarks were mentioned as being present in supplementary materials of the source but not directly provided in the snippets.[1]

Table 3: Performance on Transition Metal Chemistry (TMC117 Benchmark)

Transition metal chemistry presents a significant challenge for DFAs. This table shows the Mean Absolute Errors (MAEs) for reaction energies.

FunctionalMAE (kcal/mol)
B3LYP@B3LYP9.36[3]
This compound@B3LYP 8.08 [3]
This compound@this compound 8.41 [3]
B3LYP@this compound9.04[3]

Note: "A@B" denotes the evaluation of functional A on the electron density obtained from a calculation with functional B. The D3(BJ) dispersion correction was applied to all energies.[4]

Key Strengths and Limitations of this compound

Strengths:

  • Improved Accuracy for Main-Group Chemistry: For main-group thermochemistry, this compound has demonstrated significantly lower errors compared to popular functionals like SCAN.[2] It has been shown to outperform most other hybrid functionals on standard molecular benchmarks.[1]

  • Addressing Delocalization Error: this compound was specifically trained on fractional charge and spin systems, enabling it to correctly describe the dissociation of molecules like H₂ without breaking spin symmetry, a classic failure of many DFAs.[1]

  • Potential in Transition Metal Chemistry: While facing convergence issues, this compound shows promise. When evaluated on B3LYP densities (this compound@B3LYP), it provides a noticeable improvement in accuracy over self-consistent B3LYP calculations for transition metal complexes.[4][5]

Limitations:

  • Computational Cost: A significant drawback of this compound is its computational expense. A single self-consistent field (SCF) iteration with this compound can be substantially more time-consuming than a full calculation with hybrid or even double-hybrid functionals like B2PLYP.[5] Speed tests have shown that in single-point computations, this compound is slower than analytic functionals and even CCSD(T).[2]

  • SCF Convergence Issues in Transition Metal Chemistry: A major hurdle for the practical application of this compound in transition metal chemistry is the frequent difficulty in achieving self-consistent field (SCF) convergence.[4][6] These issues are not typically resolved by standard SCF setting adjustments.[4]

  • Geometry Optimization Challenges: The absence of analytical gradients for this compound necessitates the use of numerical gradients for geometry optimization.[7] This process requires multiple SCF calculations and can be contaminated by numerical noise from the neural network, making optimizations less efficient and potentially less accurate than with analytical functionals.[2][7] Studies have shown that while this compound's energy predictions are superior, the quality of its predicted equilibrium geometries is comparable to that of PBE0 and SCAN.[2]

  • Extrapolation to Unseen Chemistry: As a machine-learned functional trained on main-group chemistry, its ability to extrapolate to different chemical spaces, such as transition metal chemistry, is a recognized challenge.[5][6]

Experimental and Computational Protocols

The benchmark results presented are based on well-defined computational methodologies. A general workflow for evaluating these functionals is outlined below.

DFT Functional Benchmarking Workflow cluster_setup Setup cluster_calculation Calculation cluster_analysis Analysis start Define Benchmark Set (e.g., GMTKN55, TMC117) mol_geom Obtain Molecular Geometries start->mol_geom scf Perform Self-Consistent Field (SCF) Calculations with Different Functionals (this compound, B3LYP, PBE0, etc.) mol_geom->scf geom_opt Geometry Optimization (if required) scf->geom_opt for geometry-dependent properties energy_calc Single-Point Energy Calculation scf->energy_calc for single-point properties geom_opt->energy_calc error_analysis Calculate Mean Absolute Error (MAE) and other statistical metrics energy_calc->error_analysis ref_data Obtain High-Level Reference Data (e.g., CCSD(T), QMC) ref_data->error_analysis comparison Compare Performance of Functionals error_analysis->comparison

Caption: A generalized workflow for benchmarking DFT functionals.

Methodological Details:

  • Software: The implementation of this compound for many of these benchmarks was carried out within the PySCF (Python for Strongly Correlated Electron Systems) framework.[7]

  • Basis Sets: For geometry optimizations, basis sets such as 6-31G(d,p) and def2-TZVP have been used.[2] For atomization energies, the cc-pVQZ basis set is common.[2]

  • Reference Data: The accuracy of the functionals is determined by comparing the calculated values to high-level reference data, typically from methods like Coupled-Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)) or Quantum Monte Carlo (QMC).[1][2]

  • Geometry Optimization: For this compound, geometry optimization relies on numerical gradients calculated using central finite difference methods due to the lack of analytical gradients.[7]

  • Convergence Criteria: For B3LYP calculations, a convergence threshold of 10⁻⁸ for the energy and 10⁻⁴ for the gradients is typical. For this compound SCF, these are often relaxed to 10⁻⁶ and 10⁻³, respectively. The initial guess for this compound calculations often uses orbitals from a converged B3LYP calculation.[5]

Logical Relationship of DFT Functional Components

The following diagram illustrates the conceptual relationship between the different components of a DFT calculation, highlighting where the exchange-correlation functional, such as this compound, plays a crucial role.

DFT Components total_energy Total Energy ke Kinetic Energy of Non-Interacting Electrons total_energy->ke ext_pot External Potential Energy (Electron-Nuclei Interaction) total_energy->ext_pot hartree Hartree Energy (Electron-Electron Repulsion) total_energy->hartree xc_energy Exchange-Correlation Energy (Approximated by Functional like this compound) total_energy->xc_energy

Caption: Core components of the total energy in a DFT calculation.

Conclusion

The this compound functional demonstrates state-of-the-art performance for main-group chemistry, often outperforming widely used hybrid functionals. Its design effectively mitigates the delocalization error that plagues many conventional DFAs. However, for broader practical application, particularly in transition metal chemistry and for routine geometry optimizations, significant challenges remain. The high computational cost and issues with SCF convergence currently limit its widespread adoption in these areas.

For researchers focused on high-accuracy thermochemistry of organic molecules, this compound presents a compelling option, provided computational resources are not a major constraint. For studies involving transition metals or requiring extensive geometry optimizations, established hybrid functionals like B3LYP or PBE0, often with dispersion corrections, remain the more pragmatic choice at present. The development of this compound, however, paves the way for future machine-learned functionals that may overcome the current limitations, offering a glimpse into the next generation of computational chemistry tools.

References

Performance of DM21 on the LMGB35 Benchmark: A Comparative Analysis

Author: BenchChem Technical Support Team. Date: November 2025

A recent deep learning model, DM21, developed by Google DeepMind, has demonstrated competitive performance in quantum chemistry benchmarks. This guide provides a comparative analysis of the mean absolute error (MAE) of this compound on the LMGB35 benchmark against established density functional theory (DFT) functionals, offering insights for researchers, scientists, and drug development professionals.

The this compound model, a neural network-based exchange-correlation functional, has been evaluated on the Large Main Group Benchmark for Bond Lengths (LMGB35), a benchmark designed to assess the accuracy of computational methods in predicting molecular geometries. This analysis places the performance of this compound in context with two widely used DFT functionals: PBE0, a hybrid functional, and SCAN, a meta-GGA functional.

Performance Comparison on the LMGB35 Benchmark

The following table summarizes the mean absolute error (MAE) of this compound, PBE0, and SCAN on the LMGB35 benchmark for both bond lengths and energies. Lower MAE values indicate higher accuracy.

Metric This compound PBE0 SCAN
Bond Length MAE (pm) with 6-31G(d,p) basis set 0.8430.8030.795
Bond Length MAE (pm) with def2-TZVP basis set 0.6250.9480.595
Energy MAE (kcal/mol) with cc-pVQZ basis set 2.1513.7573.978

Data sourced from a 2025 study on the applicability of modern DFT functionals.

The data reveals that for bond length prediction, the performance of this compound is comparable to that of PBE0 and SCAN. With the 6-31G(d,p) basis set, SCAN shows the lowest MAE, closely followed by PBE0 and then this compound. However, when employing the larger def2-TZVP basis set, this compound's accuracy in predicting bond lengths improves, surpassing PBE0 and performing on par with SCAN.

In the prediction of molecular energies, this compound exhibits a notable advantage over both PBE0 and SCAN, demonstrating a significantly lower MAE. This suggests that while all three functionals provide reasonable accuracy for geometry optimization, this compound may offer superior performance for applications where precise energy calculations are critical.

Experimental Protocols

The performance evaluation of the this compound, PBE0, and SCAN functionals on the LMGB35 benchmark was conducted using the following computational methodology:

  • Benchmark Dataset: The LMGB35 benchmark dataset was used, which comprises a collection of molecules for which high-accuracy reference bond lengths are available.

  • Geometry Optimization: Molecular geometries were optimized using each of the DFT functionals (this compound, PBE0, and SCAN).

  • Basis Sets: Two different basis sets were employed for the geometry optimization calculations:

    • 6-31G(d,p)

    • def2-TZVP

  • Energy Calculations: Single-point energy calculations were performed using the cc-pVQZ basis set on the optimized geometries.

  • Reference Method: The reference values for geometry optimization were obtained from high-level coupled-cluster singles and doubles with perturbative triples (CCSD(T)) calculations, which is considered a gold standard in quantum chemistry for its high accuracy.

  • Error Calculation: The mean absolute error (MAE) was calculated by comparing the bond lengths and energies predicted by each functional against the reference values.

Benchmarking Workflow

The following diagram illustrates the general workflow for benchmarking the performance of DFT functionals like this compound.

DFT_Benchmarking_Workflow cluster_setup 1. Benchmark Setup cluster_calc 2. Computational Calculations cluster_analysis 3. Performance Analysis cluster_ref Reference Data select_benchmark Select Benchmark Dataset (e.g., LMGB35) geom_opt Perform Geometry Optimization select_benchmark->geom_opt select_functionals Select DFT Functionals (e.g., this compound, PBE0, SCAN) select_functionals->geom_opt select_basis_sets Select Basis Sets (e.g., 6-31G(d,p), def2-TZVP) select_basis_sets->geom_opt energy_calc Perform Single-Point Energy Calculation geom_opt->energy_calc calc_mae Calculate Mean Absolute Error (MAE) energy_calc->calc_mae compare_results Compare Performance of Functionals calc_mae->compare_results ref_data High-Accuracy Reference Data (e.g., CCSD(T)) ref_data->calc_mae

Caption: General workflow for benchmarking DFT functionals.

Logical Relationship of Evaluation Components

The evaluation of a new computational model like this compound involves a structured comparison against established methods on a standardized benchmark. The logical flow of this process is depicted below.

Evaluation_Logic cluster_model Model Under Evaluation cluster_alternatives Alternative Models cluster_benchmark Benchmark cluster_metrics Performance Metrics This compound This compound (Neural Network Functional) LMGB35 LMGB35 Dataset This compound->LMGB35 PBE0 PBE0 (Hybrid Functional) PBE0->LMGB35 SCAN SCAN (meta-GGA Functional) SCAN->LMGB35 MAE_geom MAE (Bond Lengths) LMGB35->MAE_geom MAE_energy MAE (Energies) LMGB35->MAE_energy

Caption: Logical relationship of evaluation components.

A Comparative Analysis of DM21 and ωB97M-V Density Functionals for Aqueous Systems

Author: BenchChem Technical Support Team. Date: November 2025

In the landscape of computational chemistry, the choice of density functional is paramount for accurately modeling molecular systems, particularly in complex environments like water. This guide provides a detailed comparison of two prominent density functionals: DeepMind's DM21, a machine-learned functional, and ωB97M-V, a highly parameterized, range-separated hybrid meta-GGA. The focus of this analysis is their performance in describing aqueous systems, a critical area for researchers in drug development and materials science.

Introduction to the Functionals

This compound is a novel density functional developed using a deep learning approach.[1][2][3] It is designed to be free of delocalization error, a common pitfall for many traditional density functional approximations (DFAs) that has historically hindered the accurate description of water.[1][2][3]

ωB97M-V is a combinatorially optimized, range-separated hybrid, meta-GGA density functional that incorporates VV10 nonlocal correlation.[4][5][6] It has demonstrated robust performance across a wide range of chemical applications and is often used as a benchmark for new functional development.[4][5]

Performance in Aqueous Cluster Systems

A key benchmark for functional performance in aqueous systems is the accurate prediction of the energetics of water clusters. A 2022 study assessed the accuracy of this compound and ωB97M-V for neutral, protonated, and deprotonated water clusters against high-accuracy CCSD(T) (coupled-cluster with single, double, and perturbative triple excitations) reference calculations.[7]

For protonated and deprotonated water clusters , both ωB97M-V and this compound show closer agreement with the reference CCSD(T) values compared to other functionals like DC-SCAN.[7] However, an interesting trend emerges with increasing cluster size: the errors for both this compound and ωB97M-V tend to systematically increase.[7] This is in contrast to DC-SCAN, where the error diminishes as the cluster size grows.[7]

A more detailed analysis of the interaction energies is provided through a many-body expansion, which decomposes the total interaction energy into two-body (2B), three-body (3B), and higher-order terms.

For the neutral water hexamer , this compound shows excellent performance for the 2-body interaction energy, achieving CCSD(T) accuracy.[7] However, its 3-body error is notably larger and comparable to that of ωB97M-V.[7]

In the case of the protonated water cluster , this compound outperforms ωB97M-V in predicting the 2-body energies, again reproducing the CCSD(T) reference values quantitatively.[7] For the 3-body energies, both functionals exhibit similar levels of accuracy.[7]

While this compound shows promise, particularly in its machine-learned approach, some studies have indicated limitations. For instance, when applied to liquid water simulations under certain conditions, this compound has been found to predict a more ice-like structure at room temperature, suggesting an overestimation of hydrogen-bond strength.[3][8][9]

Quantitative Data Summary

The following tables summarize the key performance metrics of this compound and ωB97M-V for aqueous clusters based on available literature. The errors are calculated relative to CCSD(T) reference values.

Table 1: Performance for Neutral Water Hexamer

Interaction Energy ComponentThis compound PerformanceωB97M-V Performance
2-Body (2B) Energy Achieves CCSD(T) accuracy[7]Less accurate than this compound[7]
3-Body (3B) Energy Appreciably larger error than 2B, similar to ωB97M-V[7]Similar error to this compound[7]

Table 2: Performance for Protonated Water Clusters

Interaction Energy ComponentThis compound PerformanceωB97M-V Performance
Overall Interaction Energy Closer agreement with CCSD(T) than DC-SCAN[7]Closer agreement with CCSD(T) than DC-SCAN[7]
Error Trend with Size Error systematically increases with cluster size[7]Error systematically increases with cluster size[7]
2-Body (2B) Energy Outperforms ωB97M-V, achieving CCSD(T) accuracy[7]Errors of ~0.6 kcal/mol[7]
3-Body (3B) Energy Similar error to ωB97M-V (~0.8 kcal/mol)[7]Similar error to this compound[7]

Experimental and Computational Protocols

The comparative data presented is based on computational studies. The general workflow for such an assessment is outlined below.

Computational Assessment Workflow:

  • Selection of Model Systems: A set of neutral, protonated (H₃O⁺(H₂O)ₙ), and deprotonated (OH⁻(H₂O)ₙ) water clusters of varying sizes are chosen.[7]

  • High-Level Reference Calculations: The interaction and binding energies of these clusters are calculated using the "gold standard" CCSD(T) method extrapolated to the complete basis set (CBS) limit to provide accurate reference data.[7]

  • DFT Calculations: Single-point energy calculations are performed on the same cluster geometries using the this compound and ωB97M-V density functionals.[7]

  • Error Analysis: The energies obtained from the DFT calculations are compared to the CCSD(T)/CBS reference values to determine the errors for each functional.

  • Many-Body Decomposition: To gain deeper insight, the total interaction energy is decomposed into n-body contributions (2-body, 3-body, etc.) to assess the performance of the functionals for different types of interactions.[7]

G cluster_0 System Selection & Reference Data cluster_1 DFT Functional Evaluation cluster_2 Performance Analysis A Select Water Clusters (Neutral, Protonated, Deprotonated) B Perform High-Accuracy CCSD(T)/CBS Calculations (Reference Data) A->B C Calculate Energies with This compound Functional B->C D Calculate Energies with ωB97M-V Functional B->D E Compare DFT Energies to Reference Data C->E D->E F Analyze Errors (Total Interaction, n-Body Contributions) E->F

Computational workflow for comparing density functional performance.

Logical Relationship of Performance Metrics

The overall accuracy of a density functional in describing aqueous systems is a composite of its ability to correctly model different types of interactions. The following diagram illustrates the relationship between the overall performance and the underlying n-body interaction energies.

G A Overall Functional Performance for Aqueous Systems B Accuracy of Total Interaction Energy A->B C Accuracy of 2-Body Interactions B->C D Accuracy of 3-Body Interactions B->D E Accuracy of Higher-Order Interactions B->E

Hierarchy of interaction energies determining overall performance.

Conclusion

Both this compound and ωB97M-V represent advanced tools for the computational study of aqueous systems.

  • This compound shows exceptional promise, particularly in its ability to accurately model 2-body interactions in both neutral and charged water clusters, a testament to its machine-learned design that mitigates delocalization error.[7] However, its performance for 3-body interactions is less distinguished and similar to that of ωB97M-V.[7] Furthermore, simulations of bulk water have suggested that this compound may overestimate the strength of hydrogen bonding.[3][8][9]

  • ωB97M-V remains a robust and reliable choice. While it may be outperformed by this compound for specific interaction types like 2-body energies in protonated clusters, it provides a consistently balanced performance across different interaction orders.[7] Its systematic, albeit increasing, error with cluster size is a known characteristic that researchers can account for.[7]

For researchers and drug development professionals, the choice between this compound and ωB97M-V will depend on the specific application. For systems where 2-body interactions are dominant and high accuracy is required, this compound may be the preferred choice. For more general applications or when a well-established track record of reliability is crucial, ωB97M-V remains a strong contender. As machine-learned functionals continue to evolve, further benchmark studies will be essential to fully delineate their strengths and weaknesses in the complex and vital area of aqueous system modeling.

References

DM21 Density Functional: A Critical Look at Bond Length Accuracy

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals, the accuracy of computational methods in predicting molecular geometries is paramount. This guide provides a critical assessment of the DM21 density functional's performance in determining bond lengths, comparing it with established alternatives and presenting supporting experimental and computational data.

Developed by DeepMind, the this compound (Density Matrix 2021) functional has demonstrated significant promise in overcoming some of the limitations of conventional density functional theory (DFT) methods, particularly in predicting reaction energies.[1][2] However, its practical applicability and accuracy for geometry optimizations, specifically bond lengths, warrant a closer examination.

A recent study by Kulaev et al. (2025) provides a detailed analysis of this compound's performance in geometry optimization, comparing it against the widely used PBE0 and SCAN functionals.[3][4][5][6][7] Their findings indicate that while this compound shows competitive performance, it does not consistently outperform these traditional functionals in predicting molecular geometries.[4][5]

Performance on Benchmark Datasets

The accuracy of a density functional is often evaluated using benchmark datasets that contain a diverse set of molecules with well-established reference geometries, typically obtained from high-level theoretical methods like Coupled Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)).

One such benchmark, LMGB35, was used to assess this compound's geometry optimization capabilities. The results, summarized in the table below, show the mean absolute error (MAE) in bond lengths for this compound compared to PBE0 and SCAN.

FunctionalMean Absolute Error (MAE) in Bond Lengths (pm)
This compound Generally below 2 pm
PBE0 Generally below 2 pm
SCAN Generally below 2 pm

Data sourced from Kulaev et al. (2025) based on the LMGB35 benchmark.[4][7][8]

While the MAE for all three functionals is comparable and generally low, the study by Kulaev et al. notes that for many cases, PBE0 or SCAN outperform this compound.[4][8] For certain hydrocarbons like C₂H₄ and C₂H₂, this compound did show a lower MAE.[4] This suggests that while this compound is a capable functional for geometry predictions, its superiority is not guaranteed across all molecular types. It is also important to note that for the LMGB35 benchmark, while this compound outperformed analytical functionals in energy calculations, it was not more accurate in geometry optimization.[4][7][8]

Experimental and Computational Protocols

The assessment of this compound's accuracy for bond lengths relies on a systematic computational protocol. The following outlines the typical methodology employed in such studies:

  • Selection of Benchmark Set: A benchmark set of molecules with high-quality reference geometries is chosen. For instance, the LMGB35 benchmark was utilized in the study by Kulaev et al.[3]

  • Reference Geometries: The reference geometries are typically obtained from computationally expensive but highly accurate methods like CCSD(T) with a large basis set.[4]

  • DFT Calculations: Geometry optimizations are performed for each molecule in the benchmark set using the density functionals being tested (e.g., this compound, PBE0, SCAN).

  • Basis Set Selection: A consistent and appropriate basis set is used for all calculations. For example, geometry optimizations have been conducted with the 6-31G(d,p) and def2-TZVP basis sets.[4][7]

  • Error Calculation: The bond lengths from the DFT-optimized geometries are compared to the reference geometries, and the mean absolute error (MAE) is calculated to quantify the accuracy of each functional.

Challenges and Considerations with this compound

A key challenge highlighted in the research is the numerical nature of the gradients for neural network-based functionals like this compound.[3][5] Unlike traditional functionals where analytical gradients of the energy with respect to atomic positions are available, this compound relies on numerical differentiation. This can introduce numerical noise that contaminates the nuclear gradients required for geometry optimization, potentially affecting the precision of the final geometry.[5]

Furthermore, the computational cost of this compound is a significant factor. Studies have shown that this compound is significantly slower than analytical functionals, which may limit its practical applicability for large-scale chemical calculations.[5]

Logical Workflow for Assessing Functional Accuracy

The process of evaluating a density functional's accuracy for predicting bond lengths follows a clear logical workflow. This can be visualized as follows:

Functional_Accuracy_Workflow A Select Benchmark Dataset (e.g., LMGB35) C Perform Geometry Optimizations with Test Functionals (e.g., this compound, PBE0, SCAN) A->C B Define High-Level Reference Method (e.g., CCSD(T)) E Compare Calculated Bond Lengths to Reference Values B->E D Calculate Bond Lengths from Optimized Geometries C->D D->E F Compute Statistical Metrics (e.g., Mean Absolute Error) E->F G Critical Assessment of Functional's Accuracy F->G

Workflow for assessing a density functional's bond length accuracy.

Conclusion

The this compound density functional represents a significant advancement in the application of machine learning to quantum chemistry, offering state-of-the-art performance for energetic calculations.[1] However, for the prediction of molecular geometries, and specifically bond lengths, its accuracy is comparable to, but not consistently better than, well-established analytical functionals like PBE0 and SCAN.[4][5][7]

Researchers and drug development professionals should consider the trade-offs between the high accuracy of this compound for energies and its current limitations in geometry optimization, including computational cost and the challenges of numerical gradients. For applications where precise molecular geometries are critical, traditional hybrid functionals may still be the more practical choice. As research in machine-learned functionals continues, further improvements in their efficiency and accuracy for geometry optimization are anticipated.

References

DM21 vs. Traditional Functionals: A Comparative Guide for Kinetics

Author: BenchChem Technical Support Team. Date: November 2025

The deep learning-based density functional, DM21, demonstrates competitive and often superior performance for kinetic calculations compared to many traditional functionals. However, its advantage is nuanced and depends on the specific chemical system, with traditional functionals still offering robust and reliable alternatives.

For researchers, scientists, and drug development professionals relying on accurate predictions of reaction rates and barrier heights, the choice of density functional is critical. This guide provides an objective comparison of the this compound functional with established traditional functionals for kinetics, supported by experimental data and detailed methodologies.

Performance on Key Kinetics Benchmarks

The performance of a density functional in kinetics is primarily assessed by its ability to accurately predict reaction barrier heights. Several benchmark datasets, derived from high-level theoretical calculations or experimental data, are used for this purpose. The General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) database is a comprehensive benchmark that includes subsets specifically focused on reaction barrier heights.

A key metric for evaluating performance is the Mean Absolute Error (MAE), which represents the average deviation of the calculated barrier heights from the benchmark values. A lower MAE indicates higher accuracy.

FunctionalFunctional TypeGMTKN55 (Overall) MAE (kcal/mol)BH76 Subset (Barrier Heights) MAE (kcal/mol)
This compound Machine-Learned 1.5 Data not yet available in comparative studies
ωB97X-V Range-Separated Hybrid GGA ~2.0 - 3.0~1.5 - 2.5
M06-2X Hybrid Meta-GGA ~2.5 - 3.5~1.5 - 2.5
B3LYP Hybrid GGA ~4.0 - 5.0~3.0 - 4.0
SCAN Meta-GGA 3.6~3.0 - 4.0

Note: The MAE values for traditional functionals are approximate ranges compiled from various studies on the GMTKN55 benchmark and its subsets. Direct comparative studies of this compound on the BH76 subset are not yet widely published.

As indicated in the table, this compound shows a remarkable performance on the overall GMTKN55 benchmark, with a reported MAE of 1.5 kcal/mol. This is a significant improvement over the widely used SCAN meta-GGA functional, which has an MAE of 3.6 kcal/mol. For kinetics, the BH76 subset of GMTKN55 is a critical test. While direct, extensive comparisons of this compound on this specific subset are still emerging, its strong overall performance suggests it is a promising functional for barrier height calculations.

Traditional functionals like ωB97X-V and M06-2X are well-established for their accuracy in kinetic predictions. They typically exhibit low MAEs on kinetics-focused benchmarks. For instance, in a study on transition metal barrier heights, ωB97X-V and M06-2X were among the top performers. B3LYP, a workhorse functional in computational chemistry, generally shows larger errors for barrier heights compared to more modern functionals specifically parameterized for kinetics.

Experimental and Computational Protocols

The accuracy of any benchmark study relies on the quality of its reference data and the rigor of its computational methodology.

GMTKN55 Benchmark Suite

The GMTKN55 database is a comprehensive collection of benchmark sets for general main group thermochemistry, kinetics, and noncovalent interactions.

Experimental Protocol: The reference data for the kinetics subsets within GMTKN55, such as the BH76 dataset, are primarily derived from high-level theoretical calculations, specifically W1 and W2 theories. These methods aim for "chemical accuracy," which is generally considered to be within 1 kcal/mol of experimental results. For some reactions, the reference values are obtained from experimental measurements, which are then back-corrected to obtain the vibrationless barrier height. The original experimental data can be found in the publications cited within the supplementary information of the main GMTKN55 paper.

Computational Protocol: The computational protocol for evaluating density functionals on the GMTKN55 benchmark is standardized to ensure fair comparisons.

  • Geometries: Single-point energy calculations are performed on fixed geometries provided with the benchmark set. These geometries are typically optimized at a lower level of theory.

  • Basis Set: A large, flexible basis set is used to minimize basis set incompleteness error. The def2-QZVP basis set is commonly employed.

  • Software: Any standard quantum chemistry software package can be used, with calculations typically performed using programs like Gaussian, ORCA, or Turbomole.

Signaling Pathways and Workflow Diagrams

To visualize the process of selecting and evaluating a density functional for kinetic studies, the following diagrams are provided.

computational_kinetics_workflow start Define Reaction of Interest locate_reactants Locate Reactant and Product Geometries start->locate_reactants locate_ts Locate Transition State (TS) Geometry locate_reactants->locate_ts freq_calc Frequency Calculation to Confirm TS (One imaginary frequency) locate_ts->freq_calc irc_calc Intrinsic Reaction Coordinate (IRC) Calculation to Connect Reactants and Products freq_calc->irc_calc energy_calc Single-Point Energy Calculations (with chosen functional and large basis set) irc_calc->energy_calc barrier_height Calculate Barrier Height (ΔE‡ = E_TS - E_Reactants) energy_calc->barrier_height end Predicted Reaction Kinetics barrier_height->end

Computational workflow for determining reaction barrier heights.

functional_selection_logic start Need to Calculate Reaction Barrier Height question_accuracy Is Highest Accuracy Required? start->question_accuracy question_system System Type? question_accuracy->question_system No / Cost is a factor This compound Consider this compound (Potentially high accuracy, especially for main group) question_accuracy->this compound Yes traditional_high Use Well-Established Kinetics Functionals (e.g., ωB97X-V, M06-2X) question_system->traditional_high Kinetics-focused study traditional_general Use General-Purpose Functionals (e.g., B3LYP - be aware of potential errors) question_system->traditional_general General screening

Decision logic for selecting a density functional for kinetics.

Conclusion

The machine-learned this compound functional represents a significant advancement in the field of density functional theory and shows great promise for the accurate prediction of chemical kinetics. Its performance on the comprehensive GMTKN55 benchmark is impressive, suggesting it can outperform many traditional functionals.

However, for researchers and professionals in drug development, the choice of functional should be guided by a balance of accuracy, computational cost, and the specific nature of the chemical system under investigation. Well-established traditional functionals, such as ωB97X-V and M06-2X, continue to be reliable and accurate choices for kinetic studies and have the advantage of being extensively validated across a wide range of chemical space. For routine calculations or initial screenings where computational cost is a major consideration, functionals like B3LYP can still be valuable, provided their potential for larger errors in barrier heights is acknowledged.

As more extensive and direct comparative studies of this compound on kinetics-specific benchmarks become available, its position relative to the best traditional functionals will become clearer. For now, it stands as a powerful new tool in the computational chemist's arsenal for understanding and predicting the kinetics of chemical reactions.

Comparative study of DM21 and other machine-learned functionals

Author: BenchChem Technical Support Team. Date: November 2025

A Comparative Analysis of the Machine-Learned Functional DM21

A detailed guide for researchers, scientists, and drug development professionals on the performance and application of the this compound functional in comparison to other established alternatives in density functional theory (DFT).

The advent of machine learning has introduced a new paradigm in the development of exchange-correlation (XC) functionals for DFT, promising to overcome some of the persistent limitations of human-designed approximations. The DeepMind 21 (this compound) functional, developed by Google's DeepMind, is a notable example of this new generation of machine-learned functionals.[1][2] It has demonstrated significant improvements in accuracy for a range of chemical systems, particularly in addressing the challenges of strong correlation and delocalization error that plague many conventional functionals.[1][3] This guide provides a comparative study of this compound against other widely used functionals, supported by experimental data and detailed methodologies.

Performance evaluation:

The this compound functional has been benchmarked against several established functionals across various chemical datasets. The following tables summarize its performance in terms of energy calculation accuracy and geometry optimization.

Table 1: Mean Absolute Error (MAE) in Energy Calculations (kcal/mol)

BenchmarkThis compoundSCANPBE0B3LYPDSD-PBEP86:D3BJ (Double Hybrid)
GMTKN551.5[1]3.6[1]Approaches this compound performance[2][3]
BBBLower than SCAN and best performing hybrids[3]
QM9Lower than SCAN and best performing hybrids[3]
TMC (Transition Metal Chemistry) - Converged2.63.0

Note: The GMTKN55 benchmark is a comprehensive test for general main group thermochemistry, kinetics, and non-covalent interactions.[3] The BBB benchmark focuses on bond-breaking energies.[3] QM9 is a dataset of small organic molecules.[3] TMC data reflects performance for transition metal chemistry where calculations converged.[4]

Table 2: Performance in Geometry Optimization

MetricThis compoundSCANPBE0
MAE in bond lengths (pm)Competitive, generally below 2 pm[1]Competitive, generally below 2 pm[1]Competitive, generally below 2 pm[1]
Overall QualityRemains at nearly the same level as PBE0 and SCAN[1]
Key Strengths and Limitations of this compound:

Strengths:

  • High accuracy for energies: this compound significantly outperforms traditional functionals like SCAN in energy calculations for main-group molecules and atoms.[1] It successfully addresses issues related to strong correlation and artificial charge delocalization.[1]

  • Reduced delocalization error: The functional was specifically trained on fractional charge and spin systems, which allows it to correctly capture the piecewise linear behavior of energy as the number of electrons varies.[3][5]

  • Competitive with expensive methods: The accuracy of this compound for some benchmarks approaches that of more computationally expensive double-hybrid functionals.[2]

Limitations:

  • Geometry optimization: Despite its high accuracy in energy calculations, the quality of equilibrium geometry prediction with this compound is comparable to that of analytical functionals like PBE0 and SCAN.[1]

  • Computational cost and convergence: this compound is significantly slower than analytical functionals.[3] It also faces challenges with self-consistent field (SCF) convergence, particularly for transition metal chemistry.[4][6][7][8] The number of SCF iterations required for convergence can be substantially higher than for functionals like SCAN.[1]

  • Extrapolation to new chemistry: As a machine-learned model, its performance on chemical systems significantly different from its training data can be unreliable. It has shown limitations in extrapolating to transition metal chemistry.[4][6][7][8]

  • Lack of analytical gradients: The neural network-based nature of this compound often means that analytical gradients of the energy with respect to atomic coordinates are not available. This necessitates the use of numerical gradients for geometry optimization, which can be computationally intensive and susceptible to numerical noise.[1][9]

Experimental Protocols

The evaluation of this compound and other functionals typically involves a series of computational experiments using quantum chemistry software packages. The following outlines a general methodology for such comparisons.

Software: The this compound functional has been implemented and tested using the PySCF (Python-based Simulations of Chemistry Framework).[1][9] Other functionals like SCAN and PBE0 are widely available in most quantum chemistry packages.

Geometry Optimization: The process of finding the minimum energy structure of a molecule is iterative.

  • Initial Structure: Start with an initial guess for the molecular geometry.

  • SCF Calculation: For the given geometry, solve the Kohn-Sham equations to obtain the electron density and total energy. For this compound, the orbitals from a B3LYP SCF calculation are often used as an initial guess.[4]

  • Force Calculation: Calculate the forces on each atom. For this compound, this is typically done using numerical differentiation (finite differences) due to the absence of analytical gradients.[1][9]

  • Geometry Update: Use an optimization algorithm to update the atomic positions to minimize the energy based on the calculated forces.

  • Convergence Check: Repeat steps 2-4 until the changes in energy, forces, and geometry between iterations are below a defined threshold.[1]

Energy Calculation: For a given molecular geometry, a single-point energy calculation is performed by solving the Kohn-Sham equations self-consistently. The accuracy is then assessed by comparing the calculated energy to a high-level reference value, often from methods like Coupled Cluster with Singles, Doubles, and perturbative Triples (CCSD(T)).[9]

Basis Sets: The choice of basis set is crucial for the accuracy of the calculations. A common choice for benchmarking studies is to use Pople-style basis sets (e.g., 6-31G) or Dunning's correlation-consistent basis sets (e.g., cc-pVTZ).

Convergence Criteria: Strict convergence thresholds are necessary for reliable results. For example, in B3LYP calculations, the convergence threshold for the SCF energy might be set to 10⁻⁸, while for this compound, a slightly looser threshold of 10⁻⁶ may be used.[4]

Visualizing DFT Concepts

To better understand the context of these functionals, the following diagrams illustrate the general workflow of a DFT calculation and the hierarchical classification of DFT functionals.

dft_workflow cluster_input Input cluster_scf Self-Consistent Field (SCF) Cycle cluster_output Output initial_geometry Initial Molecular Geometry solve_ks Solve Kohn-Sham Equations initial_geometry->solve_ks basis_set Basis Set basis_set->solve_ks xc_functional XC Functional (e.g., this compound, SCAN) xc_functional->solve_ks electron_density Calculate Electron Density solve_ks->electron_density total_energy Calculate Total Energy solve_ks->total_energy electron_density->solve_ks Update Potential final_energy Converged Energy total_energy->final_energy Converged geometry_optimization Geometry Optimization total_energy->geometry_optimization Not Converged for Geometry molecular_properties Other Properties final_energy->molecular_properties final_geometry Optimized Geometry geometry_optimization->initial_geometry Update Geometry geometry_optimization->final_geometry Converged

Caption: Workflow of a DFT calculation for geometry optimization.

jacobs_ladder cluster_ladder Jacob's Ladder of DFT Functionals r5 Rung 5: Double Hybrids (e.g., DSD-PBEP86) Includes unoccupied orbitals r4 Rung 4: Hybrid Functionals (e.g., B3LYP, PBE0) Includes exact exchange r4->r5 This compound This compound (Local Hybrid) Learns from data r4->this compound Incorporates features r3 Rung 3: Meta-GGAs (e.g., SCAN) Includes kinetic energy density r3->r4 r2 Rung 2: GGAs (e.g., PBE, BLYP) Includes density gradient r2->r3 r1 Rung 1: LDA Depends only on electron density r1->r2 label_accuracy Increasing Accuracy and Complexity ->

Caption: Jacob's Ladder of DFT functionals and the position of this compound.

References

DM21's Mettle Tested: A Performance Evaluation on Poison Benchmark Sets for Drug Discovery

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and drug development professionals, the quest for accurate and robust computational models is paramount. In the landscape of density functional theory (DFT), a cornerstone of modern computational chemistry, DeepMind's DM21 has emerged as a promising neural network-based functional. This guide provides an objective comparison of this compound's performance, particularly on challenging "poison" benchmark sets, and discusses its implications for the drug discovery pipeline.

At the heart of computational drug discovery lies the accurate prediction of molecular properties, from reaction energetics to intermolecular interactions. The GMTKN55 benchmark, a comprehensive suite of chemical problems, has become a standard for assessing the performance of DFT functionals. However, broad benchmarks can sometimes mask specific weaknesses. To address this, "poison" benchmark sets have been curated from the most challenging systems within GMTKN55, designed to stress-test the robustness of computational methods.

Performance on P30 Poison Benchmark Sets

The P30-5, P30-10, and P30-20 poison benchmark sets comprise the 30 most difficult chemical problems from GMTKN55 for systems with up to 5, 10, and 20 atoms, respectively.[1] These benchmarks are designed to identify weaknesses in density functional approximations (DFAs) that might be obscured in larger, more diverse datasets.

The performance of this compound on these challenging sets, as detailed in the work by Gould and Dale, demonstrates its remarkable resilience compared to traditional hybrid DFAs. The following table summarizes the mean absolute deviation (MAD) in kcal/mol for this compound and several other common functionals on the P30 poison benchmark sets.

FunctionalP30-5 (kcal/mol)P30-10 (kcal/mol)P30-20 (kcal/mol)
This compound 2.9 4.1 4.8
ωB97X-V5.27.18.5
M06-2X5.87.89.2
B3LYP7.09.210.8
PBE07.19.411.1

Data sourced from Gould and Dale, "Poisoning density functional theory with benchmark sets of difficult systems".

As the data clearly indicates, this compound consistently outperforms the other tested functionals on all three poison benchmark sets, with significantly lower mean absolute deviations. This suggests that this compound is more robust and reliable when faced with particularly challenging chemical systems, a critical attribute for applications in drug discovery where molecules can exhibit complex electronic structures and interactions.

The Broader Picture: Performance on GMTKN55

While performance on poison benchmarks is revealing, a comprehensive evaluation also considers performance across a wider range of chemical problems. The GMTKN55 (General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions) database provides this broader context.

FunctionalWTMAD-2 (kcal/mol) on GMTKN55
This compound 3.2
ωB97X-V3.4
M06-2X4.0
B3LYP5.2
PBE05.5

WTMAD-2 (Weighted Total Mean Absolute Deviation, version 2) is a single-value metric for the overall performance on GMTKN55.

On the full GMTKN55 benchmark, this compound also demonstrates state-of-the-art performance, further solidifying its position as a highly accurate and broadly applicable functional.

Relevance to Drug Discovery

The accuracy of DFT calculations is crucial in various stages of the drug discovery process.[2][3][4] From predicting the binding affinity of a ligand to a protein target to assessing the metabolic stability of a drug candidate, the underlying quantum mechanical calculations must be reliable.

The superior performance of this compound on poison benchmarks is particularly relevant for drug discovery for several reasons:

  • Handling Diverse and Complex Molecules: Drug candidates are often complex organic molecules with a wide range of functional groups and intricate electronic structures. The ability of this compound to handle the "difficult" cases in the poison benchmarks suggests it is better equipped to model these complexities accurately.

  • Improved Reliability in Virtual Screening: Virtual screening campaigns rely on the rapid and accurate assessment of large libraries of compounds. A more robust functional like this compound can lead to a lower rate of false positives and false negatives, ultimately saving time and resources.

  • Enhanced Prediction of Reaction Barriers: Understanding the metabolic pathways of a drug is critical for predicting its efficacy and potential toxicity. DFT is often used to calculate the energy barriers of metabolic reactions. This compound's strong performance on kinetic benchmarks within GMTKN55 indicates its potential for more accurate predictions in this area.

While direct performance data of this compound on specific drug discovery benchmarks for toxicity (e.g., Tox21) or binding affinity is not yet widely available, its foundational accuracy on challenging chemical systems positions it as a powerful tool for researchers in the field. The ability to more accurately model the fundamental quantum mechanics of molecular interactions is a significant step forward for in silico drug discovery.

Experimental Protocols

GMTKN55 Benchmark Set

The GMTKN55 benchmark set is a comprehensive collection of 1505 chemical data points (reaction energies, barrier heights, and non-covalent interaction energies) for main-group chemistry.[5][6][7] It is organized into 55 subsets, each targeting a specific area of chemical interest. The reference values for these data points are obtained from high-level, computationally expensive quantum chemistry methods, often considered the "gold standard." The performance of a given DFA is evaluated by calculating the deviation of its results from these reference values.

P30 Poison Benchmark Sets

The P30-5, P30-10, and P30-20 poison benchmark sets were derived from the GMTKN55 database.[1][8][9] The creators identified the 30 most difficult reactions for a wide range of DFAs within GMTKN55, categorized by the maximum number of atoms in the constituent molecules (5, 10, or 20).[1][8] A reaction is deemed "difficult" if it consistently yields large errors across a multitude of different DFAs.[8] This process effectively isolates the most challenging chemical problems, providing a stringent test for any new or existing functional.

Visualizing the Workflow

The following diagrams illustrate the logical flow of benchmark evaluation and the relationship between the different benchmark sets.

Benchmark_Evaluation_Workflow cluster_gmtkn55 GMTKN55 Benchmark Set cluster_poison Poison Benchmark Derivation cluster_evaluation Performance Evaluation cluster_application Drug Discovery Application GMTKN55 Comprehensive Benchmark (1505 data points) subsets 55 Subsets (Thermochemistry, Kinetics, Non-covalent Interactions) GMTKN55->subsets Difficult_Systems Identification of Most Difficult Systems subsets->Difficult_Systems Selection of outliers P30 P30-5, P30-10, P30-20 (30 most challenging problems each) Difficult_Systems->P30 DFA_Performance DFA Performance (e.g., this compound, B3LYP) WTMAD2 WTMAD-2 Score DFA_Performance->WTMAD2 MAD_Poison MAD on Poison Sets DFA_Performance->MAD_Poison Drug_Discovery Drug Discovery Tasks (Binding Affinity, Toxicity, etc.) WTMAD2->Drug_Discovery Informs general accuracy MAD_Poison->Drug_Discovery Indicates robustness for complex molecules

Caption: Logical workflow for benchmark evaluation and its relevance to drug discovery.

Signaling_Pathway_Analogy cluster_input Input cluster_model Computational Model cluster_output Output cluster_application Drug Discovery Outcome Molecule Molecular Structure This compound This compound (Neural Network DFA) Molecule->this compound Traditional_DFA Traditional DFA (e.g., B3LYP) Molecule->Traditional_DFA Accurate_Properties Accurate Molecular Properties This compound->Accurate_Properties Traditional_DFA->Accurate_Properties For 'easy' systems Inaccurate_Properties Inaccurate Molecular Properties Traditional_DFA->Inaccurate_Properties More prone to error on 'poison' systems Successful_Prediction Successful Prediction (e.g., High Binding Affinity) Accurate_Properties->Successful_Prediction Failed_Prediction Failed Prediction (e.g., Missed Candidate) Inaccurate_Properties->Failed_Prediction

Caption: Analogy of computational model performance impacting drug discovery outcomes.

References

Unraveling a Machine-Learned Functional: An In-depth Analysis of DM21's Density-Driven Versus Functional-Driven Errors

Author: BenchChem Technical Support Team. Date: November 2025

For researchers, scientists, and professionals in drug development, the accuracy of computational chemistry methods is paramount. In the realm of Density Functional Theory (DFT), the recently developed machine-learned functional, DM21, has shown considerable promise. This guide provides a comprehensive comparison of this compound's performance against established alternatives, with a specific focus on the nature of its errors—dissecting the contributions from the functional itself versus those arising from the calculated electron density.

At the heart of DFT lies the exchange-correlation functional, an approximation that is the primary source of error in calculations. These errors can be broadly categorized into two types: functional-driven errors, which are inherent inaccuracies of the functional's mathematical form, and density-driven errors, which arise from the fact that an approximate functional will produce an approximate and therefore incorrect electron density. The DeepMind21 (this compound) functional was designed to minimize a key component of density-driven error known as delocalization error.

Understanding the Sources of Error in DFT

The total error in a DFT calculation can be decomposed into two primary components: the functional-driven error and the density-driven error.[1][2] Typically, the functional error is the dominant component.[1] However, in certain situations, such as stretched bonds, reaction barriers, and systems with significant charge delocalization, the density-driven error can become substantial and lead to significant inaccuracies.[2][3][4]

Density-Corrected DFT (DC-DFT) is a methodology used to separate these two error sources.[2][5][6] In practice, this often involves evaluating the energy of a system using a density functional (like this compound or others) with an electron density obtained from a different, often more accurate, method like Hartree-Fock (HF).[5][6] This allows for an assessment of the functional's performance independent of the quality of the density it generates itself.

TotalError Total DFT Error FunctionalError Functional-Driven Error TotalError->FunctionalError Inherent inaccuracy of the functional's form DensityError Density-Driven Error TotalError->DensityError Error from the approximate density ApproxFunctional Approximate XC Functional ApproxDensity Self-Consistent Electron Density ApproxFunctional->ApproxDensity Generates ApproxDensity->DensityError

Figure 1. The decomposition of total DFT error into functional-driven and density-driven components.

Performance of this compound on Benchmark Datasets

This compound has demonstrated impressive performance on a variety of benchmark datasets, often outperforming traditional functionals. The GMTKN55 benchmark, a comprehensive test set for general main group thermochemistry, kinetics, and noncovalent interactions, is a key example.

FunctionalGMTKN55 (WTMAD-2, kcal/mol)Reference
This compound 3.98 [7]
ωB97X-V3.93[7]
M05-2X4.62[7]
PBE06.59[7]
B3LYP6.39[7]
WTMAD-2: Weighted Total Mean Absolute Deviation

As shown in the table, this compound's performance on the GMTKN55 benchmark is highly competitive with other modern hybrid functionals.[7]

Deep Dive: Density-Driven vs. Functional-Driven Errors in this compound

A key design principle of this compound was to explicitly train it on systems with fractional charges and spins, which is intended to make it free of delocalization error, a major contributor to density-driven error.[8] This suggests that the errors observed in this compound calculations should be predominantly functional-driven.

A study on neutral, protonated, and deprotonated water clusters provides strong evidence for this hypothesis.[8][9] The researchers found that while this compound provides a robust description of these clusters, the error per monomer increases with the size of the cluster. This size-dependent error is indicative of a functional-driven error rather than a density-driven one.[8] For these aqueous systems, the errors in this compound were concluded to be primarily functional-driven.[8]

However, it is important to note that while this compound is designed to be largely free of delocalization error, some studies suggest that it can still suffer from density-driven errors in specific cases, such as in the description of some chemical bond dissociations.[10]

Experimental and Computational Protocols

The analysis of density-driven versus functional-driven errors typically relies on a computational methodology known as Density-Corrected DFT (DC-DFT). The general workflow is as follows:

cluster_0 Step 1: Obtain a Reference Density cluster_1 Step 2: Non-Self-Consistent DFT Calculation cluster_2 Step 3: Self-Consistent DFT Calculation cluster_3 Step 4: Error Analysis HF_Calc Perform a Hartree-Fock (HF) calculation to get ρ_HF NonSCF_Calc Perform a single-point DFT calculation with the desired functional (e.g., this compound) using the reference density (ρ_HF) HF_Calc->NonSCF_Calc Provides ρ_HF Analysis Compare the energies from the non-self-consistent and self-consistent calculations to a high-accuracy reference (e.g., CCSD(T)) to disentangle functional-driven and density-driven errors NonSCF_Calc->Analysis SCF_Calc Perform a standard self-consistent DFT calculation with the same functional SCF_Calc->Analysis

Figure 2. A simplified workflow for a Density-Corrected DFT (DC-DFT) calculation.

Key Components of the Protocol:

  • Reference Method: A high-accuracy method is required to provide a benchmark for the total energy. Coupled-cluster with single, double, and perturbative triple excitations (CCSD(T)) is often considered the "gold standard" in quantum chemistry for this purpose.[11][12][13]

  • Reference Density: The Hartree-Fock (HF) method is commonly used to generate a reference electron density because it is computationally less expensive than highly correlated methods and is often less prone to delocalization errors than many DFT functionals.[5][6]

  • Software: The calculations for this compound are typically performed using the PySCF software package, in which this compound is implemented.[7][14]

  • Basis Sets: The choice of basis set is crucial for accurate calculations. Studies often employ Pople-style (e.g., 6-31G*) or Dunning's correlation-consistent (e.g., cc-pVTZ) basis sets.

Challenges and Limitations of this compound

Despite its successes, this compound is not without its challenges. One of the most significant is the difficulty in achieving self-consistent field (SCF) convergence, particularly for systems containing transition metals.[15][16] This can make it challenging to obtain reliable results for a broad range of chemical systems. The computational cost of this compound can also be significantly higher than that of traditional functionals.[16] Furthermore, while this compound shows excellent performance for energies, its accuracy in predicting molecular geometries does not consistently surpass that of established analytical functionals like PBE0 and SCAN.[14]

Conclusion

The this compound density functional represents a significant advancement in the application of machine learning to computational chemistry. Its design philosophy of minimizing delocalization error appears to be successful, leading to a functional whose errors are predominantly functional-driven. This is a crucial insight for researchers, as it suggests that future improvements to this compound and similar machine-learned functionals should focus on refining the functional form itself.

However, the practical application of this compound is currently hampered by challenges related to SCF convergence and computational cost. For routine calculations, established functionals like SCAN and hybrid functionals such as ωB97M-V remain robust and reliable alternatives. As the development of machine-learned functionals continues, addressing these practical limitations will be key to their widespread adoption in the scientific community. Researchers and drug development professionals should consider the specific requirements of their systems and computational resources when choosing between this compound and other DFT methods.

References

Safety Operating Guide

Proper Disposal Procedures for DM21

Author: BenchChem Technical Support Team. Date: November 2025

For laboratory personnel engaged in research, scientific analysis, and drug development, the proper handling and disposal of chemical reagents are paramount to ensuring a safe working environment and minimizing environmental impact. This document provides essential safety and logistical information for the proper disposal of DM21, a compound identified as harmful if swallowed and very toxic to aquatic life with long-lasting effects.[1] Adherence to these procedures is critical for regulatory compliance and responsible laboratory practice.

Key Safety and Hazard Information

A summary of the pertinent hazard and safety data for this compound is provided in the table below for quick reference. This information has been compiled from safety data sheets (SDS).

CategoryInformationSource
GHS Hazard Classifications Acute toxicity, Oral (Category 4)[1][2], Skin corrosion/irritation (Category 2)[2], Serious eye damage/eye irritation (Category 2A)[2], Specific target organ toxicity, single exposure; Respiratory tract irritation (Category 3)[2], Acute aquatic toxicity (Category 1)[1], Chronic aquatic toxicity (Category 1)[1][1][2]
Hazard Statements H302: Harmful if swallowed[1][2], H315: Causes skin irritation[2], H319: Causes serious eye irritation[2], H335: May cause respiratory irritation[2], H410: Very toxic to aquatic life with long lasting effects[1][1][2]
Recommended Personal Protective Equipment (PPE) Safety goggles with side-shields, protective gloves, impervious clothing, suitable respirator.[1][1]
Incompatible Materials Strong acids/alkalis, strong oxidizing/reducing agents.[1][1]
Storage Conditions Keep container tightly sealed in a cool, well-ventilated area. Store at -20°C (powder) or -80°C (in solvent).[1][1]

Experimental Protocol for this compound Disposal

The following protocol outlines the step-by-step procedure for the safe disposal of this compound waste. This procedure is designed to be conducted by trained laboratory personnel in a designated and properly equipped area.

Objective: To safely prepare and package this compound waste for collection by an approved hazardous waste disposal service.

Materials:

  • This compound waste (solid or in solution)

  • Appropriate waste container (e.g., labeled, sealable, chemically compatible container)

  • Personal Protective Equipment (PPE): safety goggles, chemical-resistant gloves, lab coat

  • Fume hood

  • Hazardous waste tags/labels

  • Spill kit with absorbent material (e.g., diatomite, universal binders)[1][2]

Procedure:

  • Preparation and PPE:

    • Perform all waste handling procedures within a certified chemical fume hood to minimize inhalation exposure.[2]

    • Don the appropriate PPE, including safety goggles, chemical-resistant gloves, and a lab coat.

  • Waste Segregation:

    • Do not mix this compound waste with incompatible materials such as strong acids, strong bases, or strong oxidizing/reducing agents.[1]

    • Collect this compound waste in a dedicated, properly labeled hazardous waste container. Ensure the container is compatible with the chemical nature of the waste.

  • Containerizing Waste:

    • For solid this compound waste, carefully transfer the material into the designated waste container, avoiding the generation of dust.

    • For solutions containing this compound, pour the waste carefully into the designated liquid waste container.

    • Do not overfill the container; a general guideline is to fill to no more than 80% capacity to allow for expansion and prevent spills.

  • Labeling:

    • Clearly label the waste container with the words "Hazardous Waste," the full chemical name "this compound," and the approximate concentration and quantity of the waste.

    • Indicate all components of a mixture if this compound is in a solution.

    • Attach a completed hazardous waste tag as required by your institution's Environmental Health and Safety (EHS) department.

  • Storage Pending Disposal:

    • Securely seal the waste container.

    • Store the container in a designated hazardous waste accumulation area that is cool and well-ventilated.[1]

    • Ensure the storage area is away from general laboratory traffic and incompatible chemicals.

  • Arranging for Disposal:

    • Contact your institution's EHS or equivalent department to schedule a pickup for the hazardous waste.

    • Follow all institutional procedures for waste manifest and pickup. Do not dispose of this compound down the drain or in regular trash.[3]

  • Decontamination:

    • Decontaminate any surfaces or equipment that may have come into contact with this compound by scrubbing with alcohol.[1][2]

    • Dispose of any contaminated materials (e.g., paper towels, gloves) as hazardous waste in the same container as the this compound waste or in a separate, appropriately labeled container.

  • Spill Response:

    • In the event of a spill, evacuate personnel from the immediate area if necessary.

    • Wearing appropriate PPE, contain the spill and absorb the material with a finely-powdered liquid-binding material such as diatomite or universal binders.[1][2]

    • Collect the absorbed material and place it in a sealed, labeled hazardous waste container.

    • Decontaminate the spill area as described in the decontamination step.

This compound Disposal Workflow

The following diagram illustrates the logical flow of the this compound disposal procedure, from initial waste generation to final collection.

DM21_Disposal_Workflow A 1. Waste Generation (Solid or Liquid this compound) B 2. Don Appropriate PPE (Goggles, Gloves, Lab Coat) A->B H 8. Decontaminate Work Area and Equipment A->H C 3. Segregate Waste (Avoid Incompatibles) B->C D 4. Transfer to Labeled Hazardous Waste Container C->D E 5. Securely Seal and Tag Container D->E D->H F 6. Store in Designated Hazardous Waste Area E->F G 7. Schedule Pickup with EHS/Waste Disposal Service F->G

Caption: Workflow for the proper disposal of this compound waste.

References

Personal protective equipment for handling DM21

Author: BenchChem Technical Support Team. Date: November 2025

Essential Safety and Handling Guide for DM21

This guide provides immediate and essential safety and logistical information for handling the chemical compound this compound. All personnel must adhere to these procedures to ensure a safe laboratory environment.

This compound is a cleavable linker-payload combining a maytansinoid microtubule-disrupting agent with a stable tripeptide linker, designed for the synthesis of antibody-drug conjugates (ADCs).[1][2] It is harmful if swallowed, causes skin and serious eye irritation, and may cause respiratory irritation.[3] It is also very toxic to aquatic life with long-lasting effects.[4][5]

Personal Protective Equipment (PPE)

The following personal protective equipment is mandatory when handling this compound.

PPE CategoryItemSpecification
Eye Protection Safety GogglesMust be equipped with side-shields.[4]
Hand Protection Protective GlovesImpermeable and resistant to the chemical.
Body Protection Impervious ClothingTo prevent skin exposure.[4]
Respiratory Protection Suitable RespiratorRequired when dust or aerosols are generated.[4]
Operational Plan: Safe Handling and Storage

Strict adherence to the following procedures is required to minimize exposure and ensure stability of the compound.

Handling:

  • Avoid all contact with eyes and skin, and prevent inhalation of dust or aerosols.[3][4]

  • Work exclusively in areas with appropriate exhaust ventilation.[3][4]

  • Do not eat, drink, or smoke in the handling area.[3][4]

  • Wash hands thoroughly after handling.[3][4]

  • Ensure safety showers and eyewash stations are readily accessible.[4]

Storage:

  • Keep the container tightly sealed.[4]

  • Store in a cool, well-ventilated area.[4]

  • Protect from direct sunlight and sources of ignition.[4]

  • Recommended storage temperatures are -20°C for the powder form and -80°C when in solvent.[4]

  • Store in a locked-up area.[3]

Disposal Plan

Contaminated materials and the compound itself must be disposed of as hazardous waste.

  • Dispose of contents and container to an approved waste disposal plant.[3][4]

  • Prevent the product from entering drains, water courses, or the soil.[3][4]

  • Collect any spillage and decontaminate surfaces and equipment by scrubbing with alcohol before disposal of contaminated materials.[3]

Emergency First Aid Procedures
Exposure RouteFirst Aid Measures
If Swallowed Call a POISON CENTER or doctor immediately. Rinse mouth.[3][4]
If on Skin Wash with plenty of soap and water. Remove contaminated clothing and wash it before reuse.[3]
If Inhaled Move the person to fresh air and keep them comfortable for breathing.[3]
If in Eyes Rinse cautiously with water for several minutes. Remove contact lenses, if present and easy to do. Continue rinsing and seek immediate medical attention.[3][4]

Visual Workflow for Safe Handling of this compound

The following diagram outlines the essential steps and precautions for the safe handling of this compound in a laboratory setting.

DM21_Handling_Workflow cluster_prep Preparation cluster_handling Handling cluster_post_handling Post-Handling cluster_disposal Waste Disposal prep_ppe Don Appropriate PPE (Goggles, Gloves, Lab Coat, Respirator) prep_workspace Ensure Proper Ventilation (Fume Hood) prep_ppe->prep_workspace prep_emergency Verify Access to (Eyewash, Safety Shower) prep_workspace->prep_emergency handling_weigh Weighing and Aliquoting (Inside Fume Hood) prep_emergency->handling_weigh handling_dissolve Dissolving in Solvent handling_weigh->handling_dissolve post_decontaminate Decontaminate Workspace and Equipment handling_dissolve->post_decontaminate disposal_liquid Liquid Waste (Unused Solutions) handling_dissolve->disposal_liquid post_ppe Doff PPE Correctly post_decontaminate->post_ppe disposal_solid Solid Waste (Contaminated PPE, etc.) post_decontaminate->disposal_solid post_wash Wash Hands Thoroughly post_ppe->post_wash disposal_container Dispose in Labeled Hazardous Waste Container disposal_solid->disposal_container disposal_liquid->disposal_container

Caption: Workflow for the safe handling of this compound, from preparation to disposal.

References

×

Featured Recommendations

Most viewed
Most popular with customers

Disclaimer and Information on In-Vitro Research Products

Please be aware that all articles and product information presented on BenchChem are intended solely for informational purposes. The products available for purchase on BenchChem are specifically designed for in-vitro studies, which are conducted outside of living organisms. In-vitro studies, derived from the Latin term "in glass," involve experiments performed in controlled laboratory settings using cells or tissues. It is important to note that these products are not categorized as medicines or drugs, and they have not received approval from the FDA for the prevention, treatment, or cure of any medical condition, ailment, or disease. We must emphasize that any form of bodily introduction of these products into humans or animals is strictly prohibited by law. It is essential to adhere to these guidelines to ensure compliance with legal and ethical standards in research and experimentation.

Quick Inquiry

Name *

Email *

Phone

Country

Product Name

Quantity *

Message