Mocpac
描述
准备方法
合成路线和反应条件： MOCPAC 的合成涉及多个步骤，从核心结构 4-甲基-2-氧代-2H-色烯-7-羧酸的制备开始。然后通过一系列缩合反应，将该中间体与丙酰胺基戊基链偶联。 最后一步是将氨基甲酸酯基团苄基化，得到所需产物 .
工业生产方法： this compound 的工业生产通常遵循相同的合成路线，但规模更大。该过程涉及优化反应条件，例如温度、溶剂选择和反应时间，以最大限度地提高产率和纯度。 采用重结晶和色谱等先进的纯化技术，确保化合物满足研究应用所需的标准 .
化学反应分析
反应类型： MOCPAC 经历了各种化学反应，包括：
氧化： this compound 在特定条件下可以被氧化形成相应的氧化物。
还原： 还原反应可以将 this compound 转化为其还原形式，改变其生物化学性质。
常用试剂和条件：
氧化： 常用的氧化剂包括高锰酸钾和过氧化氢。
还原： 使用硼氢化钠和氢化铝锂等还原剂。
主要产物： 由这些反应形成的主要产物取决于所用试剂和条件。 例如，氧化可能产生氧化物，而还原可能产生醇或胺 .
科学研究应用
MOCPAC 在科学研究中有着广泛的应用：
化学： 它被用作有机合成中的试剂，以及分析化学中的标准物质。
生物学： this compound 用于涉及酶动力学和蛋白质相互作用的研究。
医学： 它作为 HDAC1 底物的作用使其在基因调控和表观遗传学研究中具有价值。
作用机制
MOCPAC 通过选择性地结合组蛋白脱乙酰酶 1 (HDAC1) 来发挥其作用。这种结合抑制了组蛋白的脱乙酰作用，导致染色质结构开放，基因表达增加。 分子靶点包括组蛋白，所涉及的途径主要与染色质重塑和基因调控有关 .
类似化合物：
曲古霉素 A： 另一种 HDAC 抑制剂，但具有更广泛的特异性。
伏立诺他： 一种临床使用的 HDAC 抑制剂，在癌症治疗中应用。
罗米地辛： 一种抑制 HDAC 并用于癌症治疗的环状肽
独特性： this compound 的独特性在于其对 HDAC1 的选择性抑制，使其成为研究特定基因调控途径而不会影响其他 HDAC 的宝贵工具。 这种选择性在研究和潜在治疗应用中提供了更具针对性的方法 .
相似化合物的比较
Trichostatin A: Another HDAC inhibitor but with a broader specificity.
Vorinostat: A clinically used HDAC inhibitor with applications in cancer therapy.
Romidepsin: A cyclic peptide that inhibits HDACs and is used in cancer treatment
Uniqueness: MOCPAC’s uniqueness lies in its selective inhibition of HDAC1, making it a valuable tool for studying specific gene regulation pathways without affecting other HDACs. This selectivity provides a more targeted approach in research and potential therapeutic applications .
属性
IUPAC Name |
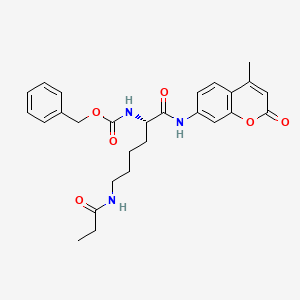
benzyl N-[(2S)-1-[(4-methyl-2-oxochromen-7-yl)amino]-1-oxo-6-(propanoylamino)hexan-2-yl]carbamate |
Source
|
|---|---|---|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
InChI |
InChI=1S/C27H31N3O6/c1-3-24(31)28-14-8-7-11-22(30-27(34)35-17-19-9-5-4-6-10-19)26(33)29-20-12-13-21-18(2)15-25(32)36-23(21)16-20/h4-6,9-10,12-13,15-16,22H,3,7-8,11,14,17H2,1-2H3,(H,28,31)(H,29,33)(H,30,34)/t22-/m0/s1 |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
InChI Key |
BFDGUJKFQRJHJM-QFIPXVFZSA-N |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Canonical SMILES |
CCC(=O)NCCCCC(C(=O)NC1=CC2=C(C=C1)C(=CC(=O)O2)C)NC(=O)OCC3=CC=CC=C3 |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Isomeric SMILES |
CCC(=O)NCCCC[C@@H](C(=O)NC1=CC2=C(C=C1)C(=CC(=O)O2)C)NC(=O)OCC3=CC=CC=C3 |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
Molecular Formula |
C27H31N3O6 |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
DSSTOX Substance ID |
DTXSID10462150 |
Source
|
| Record name | MOCPAC | |
| Source | EPA DSSTox | |
| URL | https://comptox.epa.gov/dashboard/DTXSID10462150 | |
| Description | DSSTox provides a high quality public chemistry resource for supporting improved predictive toxicology. | |
Molecular Weight |
493.6 g/mol |
Source
|
| Source | PubChem | |
| URL | https://pubchem.ncbi.nlm.nih.gov | |
| Description | Data deposited in or computed by PubChem | |
CAS No. |
787549-26-2 |
Source
|
| Record name | Phenylmethyl N-[(1S)-1-[[(4-methyl-2-oxo-2H-1-benzopyran-7-yl)amino]carbonyl]-5-[(1-oxopropyl)amino]pentyl]carbamate | |
| Source | CAS Common Chemistry | |
| URL | https://commonchemistry.cas.org/detail?cas_rn=787549-26-2 | |
| Description | CAS Common Chemistry is an open community resource for accessing chemical information. Nearly 500,000 chemical substances from CAS REGISTRY cover areas of community interest, including common and frequently regulated chemicals, and those relevant to high school and undergraduate chemistry classes. This chemical information, curated by our expert scientists, is provided in alignment with our mission as a division of the American Chemical Society. | |
| Explanation | The data from CAS Common Chemistry is provided under a CC-BY-NC 4.0 license, unless otherwise stated. | |
| Record name | MOCPAC | |
| Source | EPA DSSTox | |
| URL | https://comptox.epa.gov/dashboard/DTXSID10462150 | |
| Description | DSSTox provides a high quality public chemistry resource for supporting improved predictive toxicology. | |
Retrosynthesis Analysis
AI-Powered Synthesis Planning: Our tool employs the Template_relevance Pistachio, Template_relevance Bkms_metabolic, Template_relevance Pistachio_ringbreaker, Template_relevance Reaxys, Template_relevance Reaxys_biocatalysis model, leveraging a vast database of chemical reactions to predict feasible synthetic routes.
One-Step Synthesis Focus: Specifically designed for one-step synthesis, it provides concise and direct routes for your target compounds, streamlining the synthesis process.
Accurate Predictions: Utilizing the extensive PISTACHIO, BKMS_METABOLIC, PISTACHIO_RINGBREAKER, REAXYS, REAXYS_BIOCATALYSIS database, our tool offers high-accuracy predictions, reflecting the latest in chemical research and data.
Strategy Settings
| Precursor scoring | Relevance Heuristic |
|---|---|
| Min. plausibility | 0.01 |
| Model | Template_relevance |
| Template Set | Pistachio/Bkms_metabolic/Pistachio_ringbreaker/Reaxys/Reaxys_biocatalysis |
| Top-N result to add to graph | 6 |
Feasible Synthetic Routes
体外研究产品的免责声明和信息
请注意，BenchChem 上展示的所有文章和产品信息仅供信息参考。 BenchChem 上可购买的产品专为体外研究设计，这些研究在生物体外进行。体外研究，源自拉丁语 "in glass"，涉及在受控实验室环境中使用细胞或组织进行的实验。重要的是要注意，这些产品没有被归类为药物或药品，他们没有得到 FDA 的批准，用于预防、治疗或治愈任何医疗状况、疾病或疾病。我们必须强调，将这些产品以任何形式引入人类或动物的身体都是法律严格禁止的。遵守这些指南对确保研究和实验的法律和道德标准的符合性至关重要。
![(3aS,5R,6R,6aS)-5-[(4S)-2,2-dimethyl-1,3-dioxolan-4-yl]-2,2-dimethyl-3a,5,6,6a-tetrahydrofuro[2,3-d][1,3]dioxol-6-ol](/img/structure/B1609770.png)
![7-Nitro-1,2,3,4-tetrahydro-9h-pyrido[3,4-b]indole](/img/structure/B1609773.png)
![3-(Piperidin-4-yl)-3H-imidazo[4,5-b]pyridine](/img/structure/B1609780.png)
![4-[Methyl(phenyl)amino]benzaldehyde](/img/structure/B1609781.png)
