MAOEA

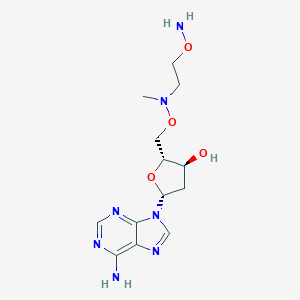
• IUPAC Name: (2R,3S,5R)-2-[[2-aminooxyethyl(methyl)amino]oxymethyl]-5-(6-aminopurin-9-yl)oxolan-3-ol
• InChI: InChI=1S/C13H21N7O4/c1-19(2-3-22-15)23-5-9-8(21)4-10(24-9)20-7-18-11-12(14)16-6-17-13(11)20/h6-10,21H,2-5,15H2,1H3,(H2,14,16,17)/t8-,9+,10+/m0/s1
• InChI Key: VRAHREWXGGWUKL-IVZWLZJFSA-N
• Canonical SMILES: CN(CCON)OCC1C(CC(O1)N2C=NC3=C(N=CN=C32)N)O
• Isomeric SMILES: CN(CCON)OC[C@@H]1[C@H](C[C@@H](O1)N2C=NC3=C(N=CN=C32)N)O
• Molecular Formula: C13H21N7O4
• DSSTOX Substance ID: DTXSID70920847
• Molecular Weight: 339.35 g/mol
• CAS No.: 112621-39-3

Description

MAOEA refers to a class of evolutionary algorithms designed to solve optimization problems with four or more conflicting objectives (many-objective optimization problems, MaOPs). These algorithms aim to balance convergence (approximating the Pareto-optimal front) and diversity (distributing solutions uniformly across the front). This compound frameworks are widely applied in domains such as recommender systems, engineering design, and drug discovery.

For example, in hybrid recommendation systems, this compound optimizes multiple objectives like accuracy, diversity, novelty, and coverage by combining collaborative filtering (CF) and content-based techniques . The algorithm employs population-based search mechanisms, where candidate solutions evolve through crossover, mutation, and environmental selection strategies. Key variants include this compound/IGD (using the Inverted Generational Distance indicator) and this compound/DS (dual selection strategy), which have demonstrated success in balancing exploration and exploitation .

Biological Activity

MAOEA, or Monoamine Oxidase Enzyme Activity, has garnered attention in recent years due to its potential therapeutic applications, particularly in the context of neurodegenerative diseases and cancer. This article explores the biological activity of this compound, focusing on its mechanisms of action, efficacy as an inhibitor of monoamine oxidases (MAOs), and its antiproliferative effects.

Overview of this compound

Monoamine oxidases (MAOs) are enzymes that catalyze the oxidative deamination of monoamines, playing a crucial role in neurotransmitter metabolism. Inhibition of MAOs can lead to increased levels of neurotransmitters such as serotonin, norepinephrine, and dopamine, which are critical in treating mood disorders and neurodegenerative diseases.

This compound primarily functions as an inhibitor of MAO-A and MAO-B isozymes. The inhibition mechanism can be competitive or non-competitive, depending on the compound structure. Recent studies have shown that certain derivatives exhibit potent inhibitory activity against both isoforms.

Key Findings:

• Inhibition Potency : Compounds designed as MAO inhibitors displayed half-maximal inhibitory concentration (IC50) values ranging from 0.038 μM to 0.077 μM for MAO-A and 0.040 μM to 0.072 μM for MAO-B .
• Reversibility : The inhibition is often reversible, which is advantageous for therapeutic applications .
• Time-Dependence : Studies indicate that some inhibitors do not exhibit time-dependent behavior, suggesting a stable interaction with the enzyme .

Antiproliferative Activity

In addition to its role as an MAO inhibitor, this compound has demonstrated significant antiproliferative effects on various cancer cell lines. This dual action makes it a candidate for multi-targeted therapies.

Case Studies:

• LN-229 Glioblastoma Cells : Compounds exhibiting strong MAO inhibition also showed cytotoxic effects on LN-229 glioblastoma cells with a growth inhibition (GI50) value of less than 1 μM . This suggests that the overexpression of MAOs in glioblastoma may be targeted effectively using these compounds.
• Mechanisms of Cytotoxicity : The cytotoxic effects were attributed not only to MAO inhibition but also potentially to other cellular pathways influenced by the compounds .

Table 1: Inhibitory Activity of Selected Compounds on MAOs

Compound	IC50 (MAO-A)	IC50 (MAO-B)	Remarks
Compound 3a	0.051 μM	0.048 μM	Potent dual inhibitor
Compound 3c	0.038 μM	0.040 μM	Stronger against MAO-A
Compound 3e	0.077 μM	0.072 μM	Effective but less potent

Table 2: Antiproliferative Effects on LN-229 Cells

Compound	GI50 (μM)	Mechanism
Compound 4	<1	MAO inhibition + other targets
Compound 5	<1	Primarily MAO inhibition

Comparison with Similar Compounds

Comparison with Similar Algorithms

Performance Metrics and Test Suites

MAOEAs are benchmarked on standardized test suites (e.g., DTLZ, WFG, MaF) using metrics like IGD+ (convergence and diversity) and HV (Hypervolume, measuring dominated space). Below is a comparative analysis of MAOEA variants against state-of-the-art algorithms:

Table 1: Key Performance Comparisons

Algorithm	Strengths	Weaknesses	Test Problems (Best Performance)	Source
This compound/IGD	Excels on linear Pareto fronts (e.g., DTLZ1, DTLZ7); competitive HV scores	Struggles with convex/concave PFs (e.g., WFG2, WFG3)	Wins 9/12 cases on linear PFs
NSGA-III	Robust on concave PFs; low computational complexity	Poor diversity on disconnected or degenerate PFs (e.g., WFG3)	Dominates WFG8 (8-objective)
MOEA/D	Effective decomposition-based approach; scalable to high dimensions	Sensitive to weight vector distribution; struggles with multimodal PFs	Best on DTLZ4 (15-objective)
ASES	Integrates Pareto dominance and decomposition; superior IGD/HV	Limited testing on irregular PFs	Wins 27/52 test instances (HV and IGD)
This compound/d2	Dual-distance mechanism improves diversity and convergence	Higher computational cost	Outperforms NSGA-III on DTLZ1-DTLZ4
RVEA	Reference vector adaptation for dynamic PF shapes	Poor performance on high-dimensional MaOPs (>15 objectives)	Best on WFG6 (15-objective)

Case Studies

Linear Pareto Fronts (DTLZ1, DTLZ7)

• This compound/IGD achieves the best HV scores on 20-objective DTLZ3 and linear PFs due to its IGD-based reference point sampling . However, it underperforms on WFG2 (convex PF) compared to RVEA and NSGA-III .
• MOEA/TS (Three States) dominates 52 test cases, including DTLZ and WFG suites, by balancing exploration and exploitation phases .

Irregular Pareto Fronts (WFG3, MaF1)

• LSEA (Local Search Evolutionary Algorithm) outperforms This compound/IGD and NSGA-III on 25/36 test instances with irregular PFs (e.g., MaF1–MaF9) through adaptive boundary selection .
• This compound/IS-DED (Indicator Selection and Density Evaluation Deletion) demonstrates superior diversity on WFG4–WFG9 (concave PFs) by combining ε-indicator selection and density-based deletion .

Computational Complexity

• NSGA-II and NSGA-III have lower complexity ($O(MN^2)$) but struggle with >10 objectives due to non-dominated sorting inefficiencies .
• HypE (Hypervolume Estimator) suffers from exponential complexity in high dimensions, whereas This compound/IGD maintains efficiency using IGD’s linear computational cost .