Bicep
Description
BenchChem offers high-quality this compound suitable for many research applications. Different packaging options are available to accommodate customers' requirements. Please inquire for more information about this compound including the price, delivery time, and more detailed information at info@benchchem.com.
Properties
CAS No. |
59316-87-9 |
|---|---|
Molecular Formula |
C23H36Cl2N6O2 |
Molecular Weight |
499.5 g/mol |
IUPAC Name |
2-chloro-N-(2-ethyl-6-methylphenyl)-N-(1-methoxypropan-2-yl)acetamide;6-chloro-4-N-ethyl-2-N-propan-2-yl-1,3,5-triazine-2,4-diamine |
InChI |
InChI=1S/C15H22ClNO2.C8H14ClN5/c1-5-13-8-6-7-11(2)15(13)17(14(18)9-16)12(3)10-19-4;1-4-10-7-12-6(9)13-8(14-7)11-5(2)3/h6-8,12H,5,9-10H2,1-4H3;5H,4H2,1-3H3,(H2,10,11,12,13,14) |
InChI Key |
NZJFTRDXVFTTGC-UHFFFAOYSA-N |
SMILES |
CCC1=CC=CC(=C1N(C(C)COC)C(=O)CCl)C.CCNC1=NC(=NC(=N1)Cl)NC(C)C |
Canonical SMILES |
CCC1=CC=CC(=C1N(C(C)COC)C(=O)CCl)C.CCNC1=NC(=NC(=N1)Cl)NC(C)C |
Synonyms |
primextra |
Origin of Product |
United States |
Foundational & Exploratory
Bicep compound mechanism of action
An in-depth search for a compound referred to as "Bicep" within the context of drug development and molecular biology has yielded no specific information. The scientific literature and public databases do not appear to contain a compound with this designation. The term "this compound" is predominantly associated with the biceps brachii muscle in anatomical and physiological contexts.
It is possible that "this compound" may be an internal codename, a very recent discovery not yet in the public domain, or a misspelling of another compound. Without a specific, recognized compound name, it is not possible to provide the requested in-depth technical guide on its mechanism of action, associated data, and signaling pathways.
To receive the requested information, please provide the correct or alternative name of the compound of interest. Once a valid compound is identified, a comprehensive technical guide can be compiled, adhering to the specified requirements for data presentation, experimental protocols, and visualizations.
An In-depth Technical Guide to the Core Components of Bicep II Magnum® Herbicide
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of the active ingredients in the herbicide Bicep II Magnum®, focusing on their chemical structures, physicochemical properties, mechanisms of action, and relevant experimental protocols. This compound II Magnum® is a widely used herbicide for the control of broadleaf and grassy weeds in various crops.[1] Its efficacy is derived from the synergistic action of its two primary components: Atrazine and S-metolachlor.
Chemical Identity and Physicochemical Properties
The two active ingredients in this compound II Magnum®, Atrazine and S-metolachlor, have distinct chemical structures and properties that dictate their behavior in the environment and their biological activity.
1.1 Atrazine
Atrazine is a triazine herbicide used for selective control of broadleaf and some grassy weeds.[2][3]
-
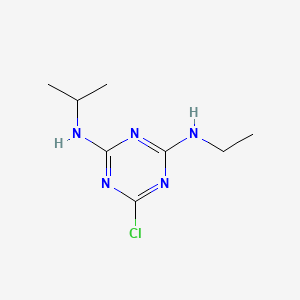
IUPAC Name: 6-chloro-N2-ethyl-N4-(propan-2-yl)-1,3,5-triazine-2,4-diamine[2]
-
Chemical Structure:
1.2 S-Metolachlor
S-metolachlor is a chloroacetanilide herbicide, primarily effective against grasses and some broadleaf weeds.[1][8] It is the S-isomer of metolachlor, which has higher herbicidal activity than the R-isomer.[8]
-
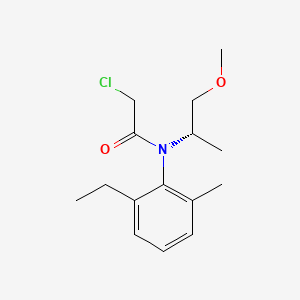
IUPAC Name: 2-chloro-N-(2-ethyl-6-methylphenyl)-N-[(2S)-1-methoxypropan-2-yl]acetamide[9]
-
Chemical Structure:
1.3 Physicochemical Data
The following tables summarize the key physicochemical properties of Atrazine and S-metolachlor.
Table 1: Physicochemical Properties of Atrazine
| Property | Value | References |
| Molecular Weight | 215.68 g/mol | [7] |
| Melting Point | 173-175 °C | [7] |
| Boiling Point | 200 °C | [11] |
| Water Solubility | 33 mg/L at 25°C | [12] |
| Vapor Pressure | 0.04 mPa at 20°C | [13] |
| log Kow | 2.6 | [7] |
Table 2: Physicochemical Properties of S-Metolachlor
| Property | Value | References |
| Molecular Weight | 283.79 g/mol | [9][10] |
| Freezing Point | -61.1 °C | [14] |
| Boiling Point | Approx. 334 °C | [14] |
| Water Solubility | 488 mg/L at 22°C | [15] |
| Vapor Pressure | 3.7 x 10⁻³ Pa at 25°C | [14] |
| log Kow | 3.1 | [9] |
Mechanism of Action and Signaling Pathways
2.1 Atrazine: Inhibition of Photosynthesis
Atrazine's primary mode of action in plants is the inhibition of photosynthesis.[3][5][16] It binds to the plastoquinone-binding protein (D1 protein) in Photosystem II (PSII) of the chloroplast thylakoid membranes.[2][16] This binding blocks the electron transport from QA to QB, thereby inhibiting CO₂ fixation and the production of ATP and NADPH₂, which are essential for plant growth.[16] The disruption of electron flow leads to the formation of reactive oxygen species, causing oxidative damage and ultimately plant death.[2][3]
References
- 1. S-Metolachlor Mode of Action: How It Works for Weed Control & OEM Supply [allpesticides.com]
- 2. Atrazine - Wikipedia [en.wikipedia.org]
- 3. fbn.com [fbn.com]
- 4. researchgate.net [researchgate.net]
- 5. How Atrazine Enhances Weed Control in Modern Agriculture [jindunchemical.com]
- 6. Atrazine [webbook.nist.gov]
- 7. Atrazine | C8H14ClN5 | CID 2256 - PubChem [pubchem.ncbi.nlm.nih.gov]
- 8. S-metolachlor - Revista Cultivar [revistacultivar.com]
- 9. S-Metolachlor | C15H22ClNO2 | CID 11140605 - PubChem [pubchem.ncbi.nlm.nih.gov]
- 10. scbt.com [scbt.com]
- 11. Atrazine CAS#: 1912-24-9 [m.chemicalbook.com]
- 12. NCCOS | Data Collection [products.coastalscience.noaa.gov]
- 13. publications.iarc.who.int [publications.iarc.who.int]
- 14. ec.europa.eu [ec.europa.eu]
- 15. ars.usda.gov [ars.usda.gov]
- 16. Aatrex / atrazine | CALS [cals.cornell.edu]
Pharmacological Properties of "Bicep": A Review of Current Scientific Understanding
Executive Summary: A comprehensive search of scientific and pharmacological literature reveals that there is no recognized pharmacological substance or drug known as "Bicep." The term "biceps" predominantly refers to the biceps brachii, a large muscle in the upper arm.[1] While various pharmacological agents can affect the biceps muscle, the muscle itself is not a therapeutic agent. This document will address the common contexts in which "this compound" appears in scientific literature and clarify the absence of a pharmacological agent by this name.
The term "this compound" has been identified in other, non-pharmacological contexts, including "this compound II Magnum," a herbicide containing atrazine and S-metolachlor.[2] Additionally, research has been conducted on signaling pathways within the biceps muscle related to exercise and muscle growth.[3][4] However, these studies do not refer to an external pharmacological agent named "this compound."
The Biceps Brachii Muscle
The biceps brachii is a prominent muscle located in the anterior compartment of the upper arm.[1] Its primary functions are flexion of the elbow and supination of the forearm.[1] The muscle is a frequent subject of study in biomechanics, sports medicine, and physiology.
Clinical Significance:
-
Biceps Tendonitis: Inflammation of the long head of the biceps tendon, often caused by overuse or injury.[5] Treatment can involve rest, anti-inflammatory drugs (NSAIDs), and steroid injections directly into the tendon sheath.[5][6]
-
Tendon Rupture: Tears of the biceps tendon can occur at the shoulder or the elbow and may require surgical repair.[5]
-
Muscle Growth and Atrophy: The biceps muscle is a key focus in studies of resistance exercise, which can induce hypertrophy (growth) through specific signaling pathways.[3][4]
Pharmacological Interventions Affecting the Biceps Muscle
While "this compound" is not a drug, various pharmacological agents are used to treat conditions affecting the biceps muscle or are studied for their effects on muscle tissue in general.
-
Corticosteroids: Injected to reduce inflammation and pain in conditions like biceps tendonitis.[5][6]
-
Nonsteroidal Anti-Inflammatory Drugs (NSAIDs): Oral or topical NSAIDs are used to manage pain and inflammation associated with biceps injuries.[5]
-
Anabolic Steroids: These drugs, related to testosterone, are known to increase muscle mass and are sometimes used illicitly by bodybuilders.[7] Their use carries significant health risks.[7]
-
Synthol: A substance injected directly into muscles, including the biceps, to increase their size.[8][9] It does not increase strength and can cause severe, permanent muscle damage.[9]
-
BPC-157: An experimental peptide that has shown potential in preclinical studies for promoting healing in musculoskeletal injuries, including muscle tears.[10]
Signaling Pathways in Skeletal Muscle
Research into the molecular mechanisms of muscle growth and adaptation has identified several key signaling pathways. These are often studied in the context of exercise, including exercises that target the biceps.
-
Resistance Exercise-Specific Signaling: Studies have identified a pathway involving MKK3b/6, p38, MK2, and mTORC1 that is activated by resistance exercise and promotes muscle growth.[3][4]
-
Calcium-Triggered Pathways: Neuromuscular activity leads to changes in intracellular calcium levels, which in turn activates signaling pathways involving calcineurin and Ca2+-calmodulin-dependent protein kinases (CaMK) that regulate gene expression related to muscle phenotype.[11][12]
The query for the pharmacological properties of "this compound" appears to be based on a misunderstanding. There is no existing pharmacological agent with this name. The scientific literature overwhelmingly uses the term "biceps" to refer to the biceps brachii muscle. For researchers and drug development professionals, the relevant areas of investigation are the pharmacological agents that can be used to treat conditions of the biceps muscle and the signaling pathways that govern muscle physiology. Future research in these areas will continue to be of high value for sports medicine, rehabilitation, and the treatment of muscle-wasting diseases.
References
- 1. Biceps - Wikipedia [en.wikipedia.org]
- 2. This compound II Magnum - Herbicide Product & Label Information | Syngenta US [syngenta-us.com]
- 3. Identification of a Resistance Exercise-Specific Signaling Pathway that Drives Skeletal Muscle Growth - PubMed [pubmed.ncbi.nlm.nih.gov]
- 4. pdfs.semanticscholar.org [pdfs.semanticscholar.org]
- 5. my.clevelandclinic.org [my.clevelandclinic.org]
- 6. Biceps Tendon Sheath Injection - StatPearls - NCBI Bookshelf [ncbi.nlm.nih.gov]
- 7. Anabolic steroid - Wikipedia [en.wikipedia.org]
- 8. indiatoday.in [indiatoday.in]
- 9. healthline.com [healthline.com]
- 10. Emerging Use of BPC-157 in Orthopaedic Sports Medicine: A Systematic Review - PMC [pmc.ncbi.nlm.nih.gov]
- 11. Brain and biceps: Understanding signaling in brain; study explores | Health [hindustantimes.com]
- 12. Interaction between signalling pathways involved in skeletal muscle responses to endurance exercise - PubMed [pubmed.ncbi.nlm.nih.gov]
A Technical Guide to Biological Target Identification Utilizing Bicyclic Peptide Technology
For Researchers, Scientists, and Drug Development Professionals
Introduction
The identification of novel biological targets is a critical first step in the development of new therapeutics. This guide provides an in-depth overview of a proprietary platform technology from Bicycle Therapeutics that utilizes bicyclic peptides, referred to as Bicycles®, for the discovery and validation of therapeutic targets. This technology offers a unique approach, combining the advantageous properties of both small molecules and biologics to address previously "undruggable" targets. This document will detail the core principles of the Bicycle platform, the experimental protocols for target identification and validation, quantitative data from preclinical and clinical studies of their pipeline candidates, and the signaling pathways of key targets.
The Bicycle® Platform: A Novel Therapeutic Modality
Bicycle Therapeutics has pioneered a novel class of medicines based on their proprietary bicyclic peptide technology. These are fully synthetic short peptides constrained by a chemical scaffold to form two loops, which stabilizes their geometry and confers high affinity and selectivity to their targets.[1][2] This constrained structure allows them to engage with a large surface area on a target protein, enabling the modulation of protein-protein interactions, a challenge for traditional small molecules.[3]
The Bicycle platform offers several key advantages:
-
High Affinity and Selectivity: Bicyclic peptides can be engineered to bind to targets with antibody-like affinity and specificity.[2]
-
Small Size: With a molecular weight of 1.5-2.5 kDa, Bicycles are significantly smaller than antibodies (~150 kDa), allowing for rapid and deep tissue penetration, a crucial factor for treating solid tumors.[4][5]
-
Tunable Pharmacokinetics: Their peptidic nature allows for a "tunable" pharmacokinetic half-life and a renal route of clearance, which can minimize liver and gastrointestinal toxicity often associated with other drug modalities.[5][6]
-
Versatile Conjugation: Bicycles can be readily conjugated to a variety of payloads, including toxins to create Bicycle Toxin Conjugates (BTCs)®, radioisotopes for Bicycle Radio Conjugates (BRCs™), and other Bicycle molecules to create multimers like Bicycle Tumor-Targeted Immune Cell Agonists (Bicycle TICAs®).[7][8]
Experimental Protocols for Target Identification and Validation
The core of Bicycle Therapeutics' target identification strategy is a proprietary phage display screening platform. This high-throughput method allows for the rapid identification of specific Bicycle molecules against a wide range of therapeutic targets.[6][9]
Phage Display Screening for Bicyclic Peptides
The process begins with the creation of vast and diverse libraries of linear peptides displayed on the surface of bacteriophage.[9][10] These libraries can contain upwards of 100 billion unique peptide sequences.[10]
Experimental Workflow:
-
Library Construction: Diverse libraries of genes encoding peptides with three cysteine residues spaced by random amino acids are fused to a phage coat protein gene.[4]
-
On-Phage Cyclization: The phage-displayed linear peptides are chemically cyclized by reacting the cysteine residues with a trivalent chemical scaffold, such as tris-(bromomethyl)benzene, to form bicyclic structures on the phage surface.[4][9] This on-phage cyclization is a key step in creating the constrained Bicycle® structure.
-
Affinity Selection (Panning): The phage library displaying the bicyclic peptides is then incubated with the target protein of interest. This can be a soluble protein or a cell-surface target on whole cells.[9][11]
-
Phage that display Bicycles with high affinity for the target will bind.
-
Non-binding phage are washed away.
-
-
Elution and Amplification: The bound phage are eluted and then amplified by infecting E. coli host cells.[12]
-
Iterative Rounds of Selection: The amplified phage are used for subsequent rounds of panning, progressively enriching the library for high-affinity binders.[4][9]
-
Hit Identification and Sequencing: After several rounds of selection, the DNA from the enriched phage is sequenced to identify the amino acid sequences of the high-affinity bicyclic peptides.[8]
-
Affinity Maturation: Initial hits can be further optimized through additional rounds of phage display where specific residues are kept constant while others are randomized to improve binding affinity and other properties.[1]
Target Validation
Once high-affinity bicyclic peptides are identified, they are synthesized and further characterized to validate their interaction with the target and their potential therapeutic effect.
Key Validation Steps:
-
Binding Affinity and Specificity Assays:
-
Surface Plasmon Resonance (SPR): To determine the binding kinetics (association and dissociation rates) and affinity (KD) of the synthesized Bicycle for its target.[1]
-
Cell-Based Binding Assays: To confirm binding to the target in a more physiological context, especially for cell-surface receptors.[13]
-
Selectivity Profiling: To assess binding against other related proteins to ensure target specificity.[13]
-
-
In Vitro Functional Assays:
-
Enzyme Inhibition Assays: For targets that are enzymes, to measure the potency (IC50) of the Bicycle in inhibiting enzymatic activity.
-
Cell Proliferation/Cytotoxicity Assays: For oncology targets, to determine the efficacy (EC50) of Bicycle Toxin Conjugates in killing cancer cells.
-
Signaling Pathway Modulation: To confirm that binding of the Bicycle to its target modulates the intended downstream signaling pathways.
-
-
In Vivo Efficacy Studies:
-
Xenograft Models: To evaluate the anti-tumor activity of Bicycle therapeutics in animal models bearing human tumors.[3][5]
-
Pharmacokinetic (PK) and Pharmacodynamic (PD) Studies: To assess the absorption, distribution, metabolism, and excretion (ADME) properties of the Bicycle molecules and their effect on the target in vivo.[14]
-
Quantitative Data Summary
The following tables summarize key quantitative data for some of Bicycle Therapeutics' clinical-stage candidates.
Table 1: Binding Affinities of Bicyclic Peptides
| Bicycle Molecule | Target | Affinity (KD) | Assay Method | Reference(s) |
| BT8009 | Nectin-4 | 2.5 nM | SPR | [1] |
| BT8009 | Nectin-4 | 12.9 nM (apparent Kd) | Cell-based | [1][13] |
| Family 2 Phage Hit | Nectin-4 | 208 nM | Phage Screen | [1] |
| Family 1 Phage Hit | Nectin-4 | 508 nM | Phage Screen | [1] |
| Family 3 Phage Hit | Nectin-4 | 888 nM | Phage Screen | [1] |
| PK15 | Kallikrein | 1.5 nM (Ki) | Enzyme Assay | [4] |
Table 2: Clinical Efficacy of Bicycle Toxin Conjugates (BTCs)®
| Drug Candidate | Target | Indication | Dose | Overall Response Rate (ORR) | Disease Control Rate (DCR) | Reference(s) |
| Zelenectide pevedotin (BT8009) | Nectin-4 | Metastatic Urothelial Cancer | 5.0 mg/m² weekly | 43% | 71% | [15] |
| Zelenectide pevedotin (BT8009) | Nectin-4 | Metastatic Urothelial Cancer | 2.5 mg/m² weekly | 25% (1 of 4 patients with PR) | 75% | [15] |
| BT5528 | EphA2 | Urothelial Cancer | 6.5-10 mg/m² every other week | 100% (2 of 2 patients with PR) | - | [15] |
| BT5528 | EphA2 | Ovarian Cancer (EphA2+) | 6.5-8.5 mg/m² every other week | 20% (1 of 5 patients with PR) | 80% (4 of 5 with antitumor activity) | [15] |
| BT5528 | EphA2 | Advanced Solid Tumors | 6.5 mg/m² every 2 weeks | 6.7% | 20.0% | [16][17] |
Table 3: Pharmacokinetic Properties of BTCs®
| Drug Candidate | Half-life (t1/2) | Clearance | Key Findings | Reference(s) |
| BT5528 | 0.4 - 0.7 hours | Renal | Rapid distribution and elimination. | [16][17] |
| MMAE (from BT5528) | 35 - 47 hours | - | Longer half-life of the payload, retained in the tumor. | [16][17] |
| BT8009 | Short systemic exposure (~1h) | Renal | Rapid tumor penetration and fast renal elimination. | [1] |
Key Signaling Pathways
Bicycle Therapeutics is targeting several key signaling pathways implicated in cancer progression. Below are simplified diagrams of these pathways.
Nectin-4 Signaling Pathway
Nectin-4 is a cell adhesion molecule that is overexpressed in various cancers and is involved in cell proliferation, migration, and angiogenesis.[18][19] It can activate the PI3K/AKT signaling pathway, which is a central regulator of cell growth and survival.[18][19][20][21]
EphA2 Signaling Pathway
EphA2 is a receptor tyrosine kinase that is often overexpressed in cancer and is associated with poor prognosis.[15] Its signaling can promote cell proliferation, migration, and invasion.[22]
MT1-MMP Signaling Pathway
Membrane Type 1 Matrix Metalloproteinase (MT1-MMP) is a transmembrane enzyme that degrades components of the extracellular matrix, facilitating cancer cell invasion and metastasis.[23] It is also involved in intracellular signaling that promotes cell migration.[24][25]
CD137 Signaling Pathway in T-cells (Target for Bicycle TICAs®)
CD137 (also known as 4-1BB) is a co-stimulatory molecule expressed on activated T-cells. Its agonism leads to T-cell proliferation and enhances their anti-tumor activity. Bicycle TICAs® are designed to co-engage a tumor antigen (like Nectin-4) and CD137 on T-cells, leading to tumor-localized immune activation.
Conclusion
The Bicycle® platform represents a significant advancement in the field of drug discovery, offering a versatile and powerful tool for the identification and validation of novel biological targets. The ability to rapidly screen vast libraries of bicyclic peptides and generate drug candidates with a unique combination of properties opens up new avenues for targeting diseases that have been intractable to traditional therapeutic modalities. The preclinical and clinical data for Bicycle Therapeutics' pipeline candidates demonstrate the potential of this technology to deliver highly potent and selective therapies with favorable safety profiles. This guide provides a foundational understanding of the Bicycle platform and its application in modern drug development, intended to aid researchers and scientists in this dynamic field.
References
- 1. pubs.acs.org [pubs.acs.org]
- 2. bicycletherapeutics.com [bicycletherapeutics.com]
- 3. Discovery of BT8009: A Nectin-4 Targeting Bicycle Toxin Conjugate for the Treatment of Cancer - PubMed [pubmed.ncbi.nlm.nih.gov]
- 4. bicycletherapeutics.com [bicycletherapeutics.com]
- 5. bicycletherapeutics.com [bicycletherapeutics.com]
- 6. bicycletherapeutics.com [bicycletherapeutics.com]
- 7. ascopubs.org [ascopubs.org]
- 8. Screening of structurally diverse bicyclic peptide libraries by phage display [infoscience.epfl.ch]
- 9. bicycletherapeutics.com [bicycletherapeutics.com]
- 10. Generation of a 100-billion cyclic peptide phage display library having a high skeletal diversity - PubMed [pubmed.ncbi.nlm.nih.gov]
- 11. bicycletherapeutics.com [bicycletherapeutics.com]
- 12. life.sjtu.edu.cn [life.sjtu.edu.cn]
- 13. BT8009; A Nectin-4 Targeting Bicycle Toxin Conjugate for Treatment of Solid Tumors - PMC [pmc.ncbi.nlm.nih.gov]
- 14. MMAE Delivery Using the Bicycle Toxin Conjugate BT5528 - PubMed [pubmed.ncbi.nlm.nih.gov]
- 15. onclive.com [onclive.com]
- 16. ascopubs.org [ascopubs.org]
- 17. Results From First-in-Human Phase I Dose-Escalation Study of a Novel Bicycle Toxin Conjugate Targeting EphA2 (BT5528) in Patients With Advanced Solid Tumors - PubMed [pubmed.ncbi.nlm.nih.gov]
- 18. Nectin-4 promotes gastric cancer progression via the PI3K/AKT signaling pathway - PubMed [pubmed.ncbi.nlm.nih.gov]
- 19. Nectin-4: New Antibody-Drug Conjugate (ADC) Target | Biopharma PEG [biochempeg.com]
- 20. Frontiers | Therapeutic prospects of nectin-4 in cancer: applications and value [frontiersin.org]
- 21. researchgate.net [researchgate.net]
- 22. researchgate.net [researchgate.net]
- 23. The Diverse Pathways for Cell Surface MT1-MMP Localization in Migratory Cells - PMC [pmc.ncbi.nlm.nih.gov]
- 24. mdpi.com [mdpi.com]
- 25. MEMBRANE TYPE 1-MATRIX METALLOPROTEINASE (MT1-MMP) IDENTIFIED AS A MULTIFUNCTIONAL REGULATOR OF VASCULAR RESPONSES - PMC [pmc.ncbi.nlm.nih.gov]
An In-depth Technical Guide to the Solubility and Stability of Biceps Muscle Proteins
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of the core principles and experimental methodologies for studying the solubility and stability of the primary proteins found in the biceps brachii muscle: actin and myosin. Understanding these properties is crucial for various applications, from fundamental muscle physiology research to the development of therapeutic agents targeting muscle disorders.
Introduction to Biceps Muscle Proteins: Actin and Myosin
The biceps brachii is a large skeletal muscle responsible for the flexion and supination of the forearm.[1] Its contractile function is driven by the interaction of two major proteins, actin and myosin, which form the myofilaments within muscle fibers.
-
Actin: A globular, multi-functional protein that polymerizes to form thin filaments (F-actin). In its monomeric form (G-actin), it is a water-soluble globular protein with a molecular weight of approximately 42 kDa.[2]
-
Myosin: A motor protein that forms the thick filaments. It is a larger, more complex protein with a molecular weight of about 520 kDa, consisting of two heavy chains and four light chains. Myosin's solubility is highly dependent on ionic strength.
The stability and solubility of these proteins are critical for maintaining muscle structure and function. Factors such as pH, temperature, and ionic strength can significantly impact their native conformation, leading to denaturation, aggregation, and loss of function.
Quantitative Data on Actin and Myosin Solubility and Stability
The following tables summarize key quantitative data regarding the solubility and stability of actin and myosin under various conditions.
Table 1: Solubility of Myosin at Varying Ionic Strengths
| Ionic Strength (mol/L NaCl) | Myosin Solubility | Observations |
| 0.0 - 0.2 | Low | Myosin tends to aggregate and form insoluble thick filaments at low ionic strength.[3] |
| 0.3 | Significantly Higher | Increased ionic strength begins to solubilize myosin filaments.[3] |
| 0.6 | High | Solubility shows an upward trend and starts to plateau.[3] |
| 0.8 - 1.0 | High (slight decrease may be observed) | High ionic strengths maintain high solubility, though a slight decrease can occur due to the salting-out effect.[3] |
Table 2: Thermal Stability of Actin and Myosin
| Protein | Condition | Melting Temperature (Tm) | Method |
| Myosin | pH 7.0, 0.5M KCl | 43 °C | Thermal Denaturation |
| pH 7.0, 0.15M KCl | 44 °C | Thermal Denaturation | |
| pH 6.5 | 37 °C | Thermal Denaturation | |
| G-Actin | Physiological Buffer | ~60.5 °C | Differential Scanning Calorimetry (DSC) |
| F-Actin | Physiological Buffer | 65 - 72 °C | Differential Scanning Calorimetry (DSC) |
Experimental Protocols
This section details the methodologies for key experiments used to assess the solubility and stability of actin and myosin.
Protein Solubility Assay
This protocol outlines a general method for determining protein solubility, which can be adapted for actin and myosin.
Objective: To quantify the amount of soluble protein in a given solvent.
Materials:
-
Purified actin or myosin
-
Buffer solutions of varying pH and ionic strength
-
Microcentrifuge
-
UV-Vis Spectrophotometer
-
Bradford or BCA protein assay reagents
Procedure:
-
Sample Preparation: Prepare a stock solution of the purified protein.
-
Solubilization: Add a known amount of the protein stock to different buffer solutions (e.g., varying pH from 4.0 to 9.0 or NaCl concentration from 0.1 M to 1.0 M).
-
Incubation: Gently mix and incubate the samples for a set period (e.g., 1 hour) at a controlled temperature (e.g., 4°C or 25°C) to allow the protein to dissolve.
-
Centrifugation: Centrifuge the samples at high speed (e.g., >100,000 x g) for a specified time (e.g., 30-60 minutes) to pellet the insoluble protein aggregates.[4]
-
Quantification: Carefully collect the supernatant containing the soluble protein. Determine the protein concentration in the supernatant using a UV-Vis spectrophotometer (measuring absorbance at 280 nm) or a colorimetric protein assay (Bradford or BCA).[4]
-
Calculation: The solubility is expressed as the concentration of protein in the supernatant (e.g., in mg/mL) or as a percentage of the total protein added.
Differential Scanning Calorimetry (DSC) for Thermal Stability
DSC is a powerful technique to measure the thermal stability of proteins by detecting the heat change that occurs during thermal denaturation.
Objective: To determine the melting temperature (Tm) and thermodynamic parameters of protein unfolding.
Materials:
-
Purified actin or myosin solution (0.1 - 2 mg/mL)[5]
-
Matched buffer solution (used for protein purification or dialysis)
-
Differential Scanning Calorimeter
Procedure:
-
Sample and Reference Preparation: Prepare the protein sample in the desired buffer. Use the exact same buffer as the reference. It is crucial to have a precisely matched buffer for accurate baseline subtraction.[5]
-
Instrument Setup:
-
Set the temperature range for the scan. This should typically start 10-20°C below the expected Tm and end 10-20°C above the final Tm.[5]
-
Set the scan rate. A typical scan rate for proteins is 60-90 °C/hour.[5]
-
Set the feedback mode and pre-scan thermostat according to the instrument's recommendations for protein samples.[5]
-
-
Data Acquisition:
-
Perform a buffer-buffer baseline scan first by loading the reference and sample cells with the matched buffer.
-
Clean the cells and load the protein sample into the sample cell and the matched buffer into the reference cell.
-
Run the temperature scan.
-
-
Data Analysis:
-
Subtract the buffer-buffer baseline from the protein scan to obtain the thermogram of protein unfolding.
-
The peak of the thermogram corresponds to the melting temperature (Tm), which is the temperature at which 50% of the protein is unfolded.
-
The area under the peak is used to calculate the calorimetric enthalpy (ΔH) of unfolding.
-
Signaling Pathways and Regulation
The solubility and stability of actin and myosin are intrinsically linked to the dynamic processes of protein synthesis and degradation within the muscle cell. These processes are tightly regulated by complex signaling pathways.
mTOR Pathway: Regulating Muscle Protein Synthesis
The mammalian target of rapamycin (mTOR) is a key kinase that regulates cell growth, proliferation, and protein synthesis in response to various stimuli, including growth factors (like IGF-1) and nutrients (amino acids). In skeletal muscle, the mTOR pathway is central to muscle hypertrophy (growth).
Caption: The mTOR signaling pathway in skeletal muscle.
Ubiquitin-Proteasome Pathway: Regulating Muscle Protein Degradation
The ubiquitin-proteasome system (UPS) is the primary pathway for the degradation of most intracellular proteins, including actin and myosin. This pathway involves the tagging of substrate proteins with a polyubiquitin chain, which marks them for degradation by the 26S proteasome.
Caption: The Ubiquitin-Proteasome Pathway for protein degradation.
Experimental Workflow for Solubility and Stability Studies
The following diagram illustrates a logical workflow for a comprehensive investigation into the solubility and stability of biceps muscle proteins.
Caption: A typical experimental workflow for protein solubility and stability studies.
Conclusion
The study of actin and myosin solubility and stability is fundamental to understanding muscle physiology and pathology. This guide has provided a technical overview of the key concepts, quantitative data, experimental protocols, and regulatory pathways involved. By employing the described methodologies, researchers can gain valuable insights into the physicochemical properties of these critical biceps muscle proteins, paving the way for advancements in both basic science and therapeutic development.
References
- 1. researchgate.net [researchgate.net]
- 2. Bioinformatics Analysis of Actin Molecules: Why Quantity Does Not Translate Into Quality? - PMC [pmc.ncbi.nlm.nih.gov]
- 3. Preliminary Exploration on the Regulatory Mechanism of Ionic Strength on Conformation and Hydration of Silver Carp Myosin - PMC [pmc.ncbi.nlm.nih.gov]
- 4. Kinetic Solubility Assays Protocol | AxisPharm [axispharm.com]
- 5. Best Practices for Differential Scanning Calorimetry of Proteins and Biopolymers | Malvern Panalytical [malvernpanalytical.com]
Early Cytotoxicity Assessment of Bispecific T-cell Engagers (BiTEs): A Technical Guide
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of the methodologies for the early in vitro assessment of cytotoxicity mediated by Bispecific T-cell Engagers (BiTEs). BiTEs represent a promising class of immunotherapy drugs that redirect a patient's T-cells to attack and eliminate cancer cells.[1][2][3] This document details the underlying mechanism of action, key experimental protocols for evaluating cytotoxicity, and guidance on data presentation and interpretation.
Mechanism of Action: Bridging T-cells and Tumor Cells
BiTEs are artificial bispecific antibodies composed of two single-chain variable fragments (scFvs) connected by a flexible linker.[1][4] One scFv targets the CD3 receptor, a component of the T-cell receptor (TCR) complex on T-cells, while the other binds to a tumor-associated antigen (TAA) expressed on the surface of cancer cells.[2][3][4]
This dual-binding capability allows the BiTE molecule to form a physical bridge, or an "immunological synapse," between a T-cell and a tumor cell.[2][5] This engagement triggers the activation of the T-cell, a process that is independent of the major histocompatibility complex (MHC) class I or co-stimulatory molecules that are typically required for T-cell activation.[1][6][7]
Upon activation, the T-cell releases cytotoxic granules containing perforin and granzymes directly into the tumor cell.[1][8] Perforin creates pores in the tumor cell's membrane, allowing granzymes to enter and initiate a cascade of events leading to apoptosis, or programmed cell death.[1][9] This potent, redirected lysis of the cancer cell is the primary mechanism behind the therapeutic effect of BiTEs.
Key In Vitro Cytotoxicity Assays
Several robust methods are available to quantify the cytotoxic potential of BiTEs in an in vitro setting. The choice of assay depends on the specific information required, throughput needs, and available laboratory equipment.
Chromium-51 (⁵¹Cr) Release Assay
This classic radioisotope assay is a sensitive method for quantifying cell-mediated cytotoxicity.[10]
Principle: Target tumor cells are pre-loaded with radioactive ⁵¹Cr. If the effector T-cells, redirected by the BiTE, lyse the target cells, the ⁵¹Cr is released into the cell culture supernatant.[10][11] The amount of radioactivity in the supernatant is directly proportional to the number of lysed cells.[10]
Experimental Protocol:
-
Target Cell Labeling:
-
Co-culture Setup:
-
Plate the ⁵¹Cr-labeled target cells in a 96-well round-bottom plate.[11][14]
-
Isolate effector cells (e.g., Peripheral Blood Mononuclear Cells - PBMCs) from healthy donors.
-
Add effector cells at various Effector-to-Target (E:T) ratios (e.g., 10:1, 5:1, 1:1).[14]
-
Add the BiTE molecule at a range of concentrations.
-
Include control wells:
-
-
Incubation: Incubate the plate for 4-6 hours at 37°C in a CO₂ incubator.[10][14]
-
Measurement:
-
Data Analysis:
-
Calculate the percentage of specific lysis using the following formula: % Specific Lysis = [(Experimental Release - Spontaneous Release) / (Maximum Release - Spontaneous Release)] x 100[11]
-
Lactate Dehydrogenase (LDH) Release Assay
This non-radioactive, colorimetric assay is a common alternative to the ⁵¹Cr release assay.[15]
Principle: Lactate dehydrogenase (LDH) is a stable cytosolic enzyme that is released into the culture medium upon cell lysis or damage to the plasma membrane.[15][16] The released LDH can be quantified by a coupled enzymatic reaction that results in the conversion of a tetrazolium salt into a colored formazan product.[15] The amount of color produced is proportional to the number of lysed cells.
Experimental Protocol:
-
Cell Plating:
-
Co-culture Setup:
-
Add effector cells at various E:T ratios.
-
Add the BiTE molecule at a range of concentrations.
-
Include control wells:
-
-
Incubation: Incubate the plate for the desired exposure period (typically 4-24 hours) at 37°C.[15]
-
Measurement:
-
Centrifuge the plate to pellet the cells.[9]
-
Transfer the supernatant to a new, optically clear 96-well plate.[9]
-
Add the LDH reaction mixture from a commercial kit to each well.[9][16]
-
Incubate at room temperature for up to 30 minutes, protected from light.[9][16]
-
Add the stop solution provided in the kit.[9]
-
Measure the absorbance at the appropriate wavelength (e.g., 490 nm) using a plate reader.[9][17]
-
-
Data Analysis:
-
Subtract the medium background absorbance from all other readings.
-
Calculate the percentage of cytotoxicity using a formula similar to the ⁵¹Cr release assay, accounting for spontaneous release from both target and effector cells.
-
Flow Cytometry-Based Apoptosis Assay (Annexin V/PI Staining)
Flow cytometry allows for the detailed analysis of individual cells and can differentiate between different stages of cell death.[18]
Principle: This method uses two key reagents:
-
Annexin V: A protein that binds to phosphatidylserine (PS).[19] In healthy cells, PS is located on the inner leaflet of the plasma membrane. During early apoptosis, PS flips to the outer leaflet, where it can be detected by fluorescently-labeled Annexin V.[19][20]
-
Propidium Iodide (PI): A fluorescent dye that can only enter cells with compromised membranes.[20] It is used to identify necrotic or late-stage apoptotic cells.
By using both reagents, one can distinguish between:
-
Early apoptotic cells: Annexin V-positive and PI-negative.[21]
-
Late apoptotic/necrotic cells: Annexin V-positive and PI-positive.[21]
Experimental Protocol:
-
Co-culture: Set up the co-culture of target cells, effector cells, and BiTEs as described in the previous assays and incubate for the desired time.
-
Cell Harvesting: Collect all cells (both adherent and suspension) from each well.[20]
-
Washing: Wash the collected cells with cold Phosphate-Buffered Saline (PBS).[20][21]
-
Staining:
-
Analysis: Analyze the cells immediately by flow cytometry.[21] Collect data on a sufficient number of events for statistical significance.
-
Data Analysis: Quantify the percentage of cells in each quadrant (healthy, early apoptotic, late apoptotic/necrotic).
Data Presentation
Quantitative data from cytotoxicity assays should be summarized in a clear and organized manner to facilitate comparison and interpretation.
Table 1: Example Presentation of BiTE-mediated Cytotoxicity Data (LDH Assay)
| BiTE Concentration | E:T Ratio | % Cytotoxicity (Mean ± SD) |
| Control BiTE | ||
| 100 ng/mL | 10:1 | 5.2 ± 1.1 |
| Test BiTE | ||
| 0.01 ng/mL | 10:1 | 25.6 ± 3.4 |
| 0.1 ng/mL | 10:1 | 58.9 ± 4.2 |
| 1 ng/mL | 10:1 | 85.3 ± 2.9 |
| 10 ng/mL | 10:1 | 88.1 ± 3.5 |
| 100 ng/mL | 10:1 | 89.5 ± 2.7 |
| 1 ng/mL | 5:1 | 62.4 ± 5.1 |
| 1 ng/mL | 1:1 | 31.7 ± 3.8 |
This table illustrates how to present dose-dependent and E:T ratio-dependent cytotoxicity. EC₅₀ values can be calculated from the dose-response curves.[23]
Table 2: Cytokine Release Profile from Co-culture Supernatants
The activation of T-cells by BiTEs also leads to the release of pro-inflammatory cytokines, which is a critical aspect of their biological activity and potential for toxicity (e.g., Cytokine Release Syndrome - CRS).[4][9][24]
| BiTE Concentration | IFN-γ (pg/mL) | TNF-α (pg/mL) | IL-6 (pg/mL) | IL-2 (pg/mL) |
| No BiTE | < 10 | < 5 | < 5 | < 20 |
| 0.1 ng/mL | 250 ± 35 | 150 ± 22 | 80 ± 15 | 450 ± 55 |
| 1 ng/mL | 1800 ± 210 | 950 ± 110 | 450 ± 60 | 2500 ± 300 |
| 10 ng/mL | 2100 ± 250 | 1100 ± 130 | 520 ± 75 | 2800 ± 350 |
Cytokine levels are typically measured from the same co-culture supernatants using methods like ELISA or multiplex bead arrays.[6][25]
Important Considerations and Troubleshooting
-
Effector-to-Target (E:T) Ratio: An excessively high E:T ratio can lead to rapid and non-specific target cell lysis. It is crucial to optimize this ratio to achieve specific killing.[9]
-
Bystander Killing: High concentrations of BiTEs can lead to over-activation of T-cells and the release of high levels of cytokines, which may induce apoptosis in nearby antigen-negative "bystander" cells.[9][26]
-
Cell Health: The health and viability of both target and effector cells prior to the assay are critical for obtaining reliable and reproducible results. High background cell death can obscure the specific cytotoxic effect.[9]
-
Target Antigen Expression: Confirm the expression level of the TAA on target cells using flow cytometry. Low or heterogeneous expression can result in weak cytotoxic responses.[9]
Conclusion
The early in vitro assessment of BiTE-mediated cytotoxicity is a critical step in the preclinical development of these potent immunotherapies. A combination of assays, including ⁵¹Cr release, LDH release, and flow cytometry, provides a comprehensive profile of a BiTE candidate's efficacy and mechanism of action. Careful experimental design, including appropriate controls and optimization of parameters like the E:T ratio, is essential for generating high-quality, interpretable data that can guide further development.
References
- 1. Bi-specific T-cell engager - Wikipedia [en.wikipedia.org]
- 2. researchgate.net [researchgate.net]
- 3. Bispecific T cell engagers for cancer immunotherapy - PMC [pmc.ncbi.nlm.nih.gov]
- 4. Bispecific T-Cell Engagers Therapies in Solid Tumors: Focusing on Prostate Cancer - PMC [pmc.ncbi.nlm.nih.gov]
- 5. researchgate.net [researchgate.net]
- 6. aacrjournals.org [aacrjournals.org]
- 7. Frontiers | Therapeutic Bispecific T-Cell Engager Antibody Targeting the Transferrin Receptor [frontiersin.org]
- 8. cumming.ucalgary.ca [cumming.ucalgary.ca]
- 9. benchchem.com [benchchem.com]
- 10. benchchem.com [benchchem.com]
- 11. revvity.com [revvity.com]
- 12. bitesizebio.com [bitesizebio.com]
- 13. Rutgers New Jersey Medical School [njms.rutgers.edu]
- 14. scispace.com [scispace.com]
- 15. LDH cytotoxicity assay [protocols.io]
- 16. sigmaaldrich.com [sigmaaldrich.com]
- 17. LDH assay kit guide: Principles and applications | Abcam [abcam.com]
- 18. bio-rad-antibodies.com [bio-rad-antibodies.com]
- 19. bitesizebio.com [bitesizebio.com]
- 20. Protocol for Apoptosis Assay by Flow Cytometry Using Annexin V Staining Method - PMC [pmc.ncbi.nlm.nih.gov]
- 21. Annexin V and PI Staining Protocol for Apoptosis by Flow Cytometry | Bio-Techne [bio-techne.com]
- 22. BestProtocols: Annexin V Staining Protocol for Flow Cytometry | Thermo Fisher Scientific - JP [thermofisher.com]
- 23. agilent.com [agilent.com]
- 24. Bispecific T-Cell Engagers (BiTEs) as Treatment of B-Cell Lymphoma - PMC [pmc.ncbi.nlm.nih.gov]
- 25. BiTE secretion from in situ-programmed myeloid cells results in tumor-retained pharmacology - PMC [pmc.ncbi.nlm.nih.gov]
- 26. Bispecific T cell engager (BiTE®) antibody constructs can mediate bystander tumor cell killing - PMC [pmc.ncbi.nlm.nih.gov]
Unraveling "Bicep": A Critical Clarification for In-Depth Cellular Pathway Analysis
An in-depth analysis of the term "Bicep" within the context of molecular and cellular biology reveals a significant ambiguity that precludes the development of a detailed technical guide as requested. While "biceps" commonly refers to the biceps brachii muscle, the scientific literature and biological databases do not identify a specific protein, gene, or signaling molecule with the standalone name "this compound." To provide an accurate and relevant technical whitepaper for researchers, scientists, and drug development professionals, clarification on the precise identity of "this compound" is essential.
Initial research into "this compound" as a biological term has yielded several possibilities, none of which definitively align with the request for a molecule that "interacts with cellular pathways" in a way that would warrant a dedicated technical guide on its own. The potential interpretations include:
-
Biceps Brachii Muscle: The most common biological meaning of "biceps" relates to the muscle in the upper arm. While the cellular and molecular biology of muscle tissue, including signaling pathways for hypertrophy and protein synthesis like the mTOR pathway, is a rich field of study, it does not center on a single entity named "this compound" that interacts with these pathways.[1][2][3][4][5][6]
-
Acronyms in Research and Biotechnology: "this compound" or similar terms can be acronyms for techniques or tools. Examples include:
-
BICePs (Bayesian Inference of Conformational Populations): An algorithm used to study the shapes of molecules.[7]
-
BiCAP (Bimolecular Complementation Affinity Purification): A method for studying interactions between proteins.[8]
-
pCMV-BICEP-4: A commercially available expression vector used in labs to study protein-protein interactions.[9]
-
-
A Novel or Proprietary Molecule: It is possible that "this compound" refers to a newly discovered protein, a drug candidate, or a proprietary molecule within a specific company or research group that has not yet entered the public scientific lexicon.
Given the highly technical and specific nature of the user's request—including demands for quantitative data, detailed experimental protocols, and Graphviz diagrams of signaling pathways—it is crucial to identify the correct "this compound." Without this clarification, any attempt to generate the requested content would be based on speculation and would not meet the standards of a scientific or technical document.
To proceed with the creation of an in-depth technical guide, please provide more specific information regarding "this compound." For example:
-
If "this compound" is an acronym, what is its full name?
-
If it is a protein or gene, what is its official symbol or accession number (e.g., from UniProt or GenBank)?
-
If it is a research project or a proprietary name, could you provide a link to a relevant publication or website?
Once the identity of "this compound" is clarified, a comprehensive and accurate technical guide on its interaction with cellular pathways can be developed to meet the detailed requirements of the intended scientific audience.
References
- 1. Biceps - Wikipedia [en.wikipedia.org]
- 2. The molecular biology behind exercise [asbmb.org]
- 3. Skeletal muscle - Wikipedia [en.wikipedia.org]
- 4. hingehealth.com [hingehealth.com]
- 5. youtube.com [youtube.com]
- 6. ssgopalganj.in [ssgopalganj.in]
- 7. Frontiers | Reconciling Simulations and Experiments With BICePs: A Review [frontiersin.org]
- 8. m.youtube.com [m.youtube.com]
- 9. sigmaaldrich.com [sigmaaldrich.com]
An In-depth Technical Guide to the Discovery and Core Principles of Bispecific Antibodies
For Researchers, Scientists, and Drug Development Professionals
This technical guide provides a comprehensive overview of the discovery, origin, and core principles of bispecific antibodies (bsAbs). It is designed for researchers, scientists, and drug development professionals seeking a detailed understanding of this rapidly evolving class of therapeutics. The guide covers the historical development, molecular formats, mechanisms of action, and key experimental protocols for the characterization of bispecific antibodies.
Discovery and Origin of Bispecific Antibodies
The concept of bispecific antibodies has a rich history, dating back over half a century. The initial idea of creating an antibody with dual specificity was first described in the 1960s.[1][2][3][4][5] These early iterations involved the chemical re-association of antigen-binding fragments (F(ab')) from two different polyclonal sera to create a bispecific F(ab')2 molecule.[2][5]
A significant breakthrough came in 1975 with the development of hybridoma technology by Köhler and Milstein, which enabled the production of monoclonal antibodies.[6][7] This technology paved the way for more defined and reproducible bispecific antibody generation. In 1983, the creation of "hybrid-hybridoma" or "quadroma" technology allowed for the production of the first monoclonal bispecific antibodies.[7] However, this method was often inefficient and resulted in a mixture of different antibody species, making purification challenging.[8]
The advent of recombinant DNA technology and antibody engineering has led to an explosion in the number of bispecific antibody formats.[5] A key innovation was the "knobs-into-holes" technology developed in 1996, which facilitated the correct pairing of two different antibody heavy chains, a critical step in producing IgG-like bispecific antibodies.[7] Today, over 100 different bispecific antibody formats have been developed, with many in preclinical and clinical development, and several already approved for therapeutic use.[1][9]
Molecular Formats of Bispecific Antibodies
Bispecific antibodies can be broadly categorized into two main classes: those with an Fc region (IgG-like) and those without (non-IgG-like).
IgG-like Bispecific Antibodies: These formats resemble conventional monoclonal antibodies and retain the Fc region, which can confer effector functions like Antibody-Dependent Cell-Mediated Cytotoxicity (ADCC) and Complement-Dependent Cytotoxicity (CDC), as well as a longer serum half-life.[10][11] Examples include:
-
Knobs-into-holes: This strategy involves engineering the CH3 domains of the two different heavy chains to promote heterodimerization.
-
DuoBody: This technology is based on a controlled Fab arm exchange process.[8]
-
Dual-Variable-Domain-IgG (DVD-Ig): A format with four antigen-binding sites, where the variable domains of two different antibodies are fused in tandem.
Non-IgG-like Bispecific Antibodies: These are typically smaller antibody fragments, which can offer advantages such as better tissue penetration.[10][12] However, their smaller size often leads to a shorter half-life in the body.[9][10] Common formats include:
-
Bispecific T-cell Engagers (BiTEs®): These molecules consist of two single-chain variable fragments (scFvs) connected by a flexible linker. One scFv binds to a tumor-associated antigen and the other binds to CD3 on T-cells.[13]
-
Diabodies: These are small, bivalent antibody fragments composed of two scFvs.[10]
-
Tandem scFv: Two scFvs are linked together on a single polypeptide chain.[10]
Mechanisms of Action
Bispecific antibodies can exert their therapeutic effects through several distinct mechanisms of action:
-
Bridging Cells: A primary application is to redirect immune effector cells, such as T-cells or Natural Killer (NK) cells, to target and kill tumor cells.[9][10] This is the mechanism employed by BiTEs, which physically link T-cells to cancer cells.[14]
-
Bridging Receptors: By simultaneously blocking two different signaling pathways, bispecific antibodies can overcome resistance mechanisms that may arise with single-target therapies.[9]
-
Bridging Factors: Some bispecific antibodies are designed to bring two factors together to form a functional complex, for example, mimicking the activity of a missing clotting factor in hemophilia A.[9]
Quantitative Data Summary
The development and characterization of bispecific antibodies involve the precise measurement of their binding and functional properties. The following tables summarize key quantitative data for representative bispecific antibodies.
Table 1: Binding Affinity of Bispecific Antibodies
| Bispecific Antibody | Target 1 | Target 2 | KD (Target 1) | KD (Target 2) | Cell Line | Reference |
| Blinatumomab | CD19 | CD3 | 1.5 nM | 79 nM | NALM-6 | F. Hoffmann-La Roche |
| Emicizumab | Factor IXa | Factor X | 1.9 nM | 110 nM | N/A | Chugai Pharmaceutical |
| Amivantamab | EGFR | MET | 0.2 nM | 1.1 nM | H1975 | Janssen Biotech |
KD (dissociation constant) is a measure of binding affinity; a lower KD indicates stronger binding.
Table 2: In Vitro Cytotoxicity of Bispecific T-cell Engagers
| BiTE Molecule | Target Cell Line | Effector:Target Ratio | EC50 | Max. Lysis (%) | Reference |
| Blinatumomab | NALM-6 (ALL) | 10:1 | 10 pg/mL | 85% | Amgen |
| Solitomab | A549 (NSCLC) | 10:1 | 50 pg/mL | 70% | Amgen |
| Teclistamab | MM.1S (Multiple Myeloma) | 10:1 | 0.2 nM | 90% | Janssen |
EC50 (half-maximal effective concentration) is the concentration of a drug that gives half of the maximal response.
Detailed Experimental Protocols
The characterization of bispecific antibodies requires a suite of specialized assays to assess their binding, potency, and functional activity.
Bispecific Antibody Production and Purification Workflow
The production of bispecific antibodies is a multi-step process that requires careful optimization to ensure the generation of a pure and active therapeutic.
Protocol:
-
Vector Construction: Genes encoding the heavy and light chains of the two specificities are cloned into mammalian expression vectors.
-
Cell Line Development: The expression vectors are transfected into a host cell line, typically Chinese Hamster Ovary (CHO) cells. Clones with high and stable expression of the bispecific antibody are selected.
-
Cell Culture Expansion: The selected clone is grown in large-scale bioreactors to produce the bispecific antibody.
-
Harvest: The cell culture supernatant containing the secreted bispecific antibody is collected.
-
Protein A Chromatography: The initial purification step for IgG-like bispecifics, which binds to the Fc region.
-
Polishing Steps: Additional chromatography steps, such as ion exchange and size exclusion chromatography, are used to remove impurities like homodimers and aggregates.[15]
-
Final Formulation: The purified bispecific antibody is formulated in a stable buffer for storage and administration.
Bispecific T-cell Engager (BiTE) Signaling Pathway
BiTEs mediate their cytotoxic effect by creating an artificial synapse between a T-cell and a tumor cell, leading to T-cell activation and tumor cell lysis.
Mechanism:
-
The BiTE molecule simultaneously binds to a tumor-associated antigen on the cancer cell and the CD3 receptor on the T-cell.[13]
-
This bridging brings the T-cell into close proximity with the tumor cell, forming an immune synapse.[3]
-
The engagement of CD3, part of the T-cell receptor (TCR) complex, initiates a signaling cascade within the T-cell, independent of MHC I presentation.[16]
-
This leads to the activation of downstream signaling molecules, resulting in the release of cytotoxic granules containing perforin and granzymes.[13]
-
Perforin creates pores in the tumor cell membrane, allowing granzymes to enter and induce apoptosis (programmed cell death).[16]
Cytotoxicity Assay Protocol
A critical in vitro assay to determine the potency of a T-cell redirecting bispecific antibody is the cytotoxicity assay.
References
- 1. tandfonline.com [tandfonline.com]
- 2. The making of bispecific antibodies - PMC [pmc.ncbi.nlm.nih.gov]
- 3. m.youtube.com [m.youtube.com]
- 4. Bispecific antibodies: design, therapy, perspectives - PMC [pmc.ncbi.nlm.nih.gov]
- 5. The development of bispecific antibodies and their applications in tumor immune escape - PMC [pmc.ncbi.nlm.nih.gov]
- 6. researchgate.net [researchgate.net]
- 7. Bispecific monoclonal antibody - Wikipedia [en.wikipedia.org]
- 8. Bispecific antibody production - ProteoGenix [proteogenix.science]
- 9. sinobiological.com [sinobiological.com]
- 10. precisepeg.com [precisepeg.com]
- 11. Bispecific Antibody Production Guide - evitria [evitria.com]
- 12. rapidnovor.com [rapidnovor.com]
- 13. Bi-specific T-cell engager - Wikipedia [en.wikipedia.org]
- 14. Bispecific T-Cell Engagers (BiTEs) | Moffitt [moffitt.org]
- 15. youtube.com [youtube.com]
- 16. Bispecific T cell engagers and their synergistic tumor immunotherapy with oncolytic viruses - PMC [pmc.ncbi.nlm.nih.gov]
Methodological & Application
Application Notes and Protocols for Bicep-Related Cell Culture Techniques
This document provides detailed application notes and experimental protocols related to two distinct "Bicep" methodologies in the context of cell culture: This compound (Bispecific Chimeric Engager Protein) technology for cancer immunotherapy and the isolation and culture of tendon-derived cells from the long head of the biceps tendon for regenerative medicine applications.
Part 1: this compound (Bispecific Chimeric Engager Protein) Technology
Introduction
Bispecific Chimeric Engager Proteins (BiCEPs) are engineered molecules designed to enhance anti-tumor immunity by simultaneously binding to an activating receptor on immune cells and a surface antigen on tumor cells.[1] This dual-targeting mechanism effectively creates a bridge between the immune cell and the cancer cell, leading to a targeted cytotoxic response. A common implementation of this compound involves linking a protein that binds to the NKG2D receptor on Natural Killer (NK) and CD8+ T cells with a ligand that targets a tumor-specific marker, such as the Epidermal Growth Factor Receptor (EGFR).[1]
Signaling Pathway
The mechanism of action for a this compound molecule targeting EGFR on tumor cells and NKG2D on immune cells involves the following signaling cascade:
Caption: this compound molecule engagement of a tumor cell and an immune cell.
Experimental Workflow
The general workflow for evaluating the efficacy of this compound molecules involves co-culturing immune cells and tumor cells in the presence of the this compound molecule and assessing tumor cell viability.
Caption: Experimental workflow for this compound in vitro efficacy testing.
Protocol: In Vitro Tumor Cell Killing Assay
This protocol outlines a method to assess the ability of this compound molecules to engage NK and T cells to kill tumor cells in vitro.[1]
Materials:
-
Target tumor cell line (e.g., expressing EGFR)
-
Immune cells (e.g., NK cells or CD8+ T cells)
-
This compound molecule
-
Cell culture medium (e.g., RPMI-1640) supplemented with 10% FBS
-
6-well tissue culture plates
-
Cell viability assay kit (e.g., MTS or Calcein-AM)
-
Incubator (37°C, 5% CO2)
Procedure:
-
Cell Seeding: Seed the target tumor cells into 6-well plates at a density of 1 x 10^5 cells per well and incubate overnight to allow for attachment.
-
Co-culture Preparation: On the following day, add the immune cells to the wells containing the tumor cells at a desired effector-to-target (E:T) ratio (e.g., 5:1).
-
This compound Addition: Add the this compound molecule to the co-culture at various concentrations. Include control wells with no this compound.
-
Incubation: Incubate the plates for 24-72 hours at 37°C with 5% CO2.
-
Viability Assessment: At the end of the incubation period, assess the viability of the tumor cells using a standard cell viability assay according to the manufacturer's instructions.
-
Data Analysis: Calculate the percentage of specific cell lysis for each this compound concentration compared to the control wells.
| Parameter | Condition | Purpose |
| Tumor Cells | 1 x 10^5 cells/well | Target for immune cell-mediated killing |
| Immune Cells | E:T ratio of 5:1 | Effector cells that mediate killing |
| This compound | Varies (e.g., 0.1-10 µg/mL) | To determine dose-dependent efficacy |
| Incubation Time | 24-72 hours | To allow for immune cell activation and killing |
Part 2: Isolation and Culture of Tendon-Derived Cells from Biceps Tendon
Introduction
The long head of the biceps (LHB) tendon is a potential source of tendon-derived cells (TDCs) for applications in tissue engineering and regenerative medicine.[2] These cells can be isolated and expanded in culture for subsequent use in research or therapeutic development.
Experimental Workflow
The process of isolating and culturing TDCs from the LHB tendon involves several key steps from tissue acquisition to cell expansion.
Caption: Workflow for isolation and culture of tendon-derived cells.
Protocol: Isolation and Culture of Human Biceps Tendon-Derived Cells
This protocol is based on a previously published method for isolating and culturing tenocytes from tendon biopsies.[3]
Materials:
-
Human long head of biceps tendon biopsy
-
Cell culture medium (DMEM/HAM's F12)
-
Phosphate-buffered saline (PBS)
-
Petri dishes
-
Incubator (37°C, 5% CO2)
-
Trypsin-EDTA
-
Hemocytometer
Procedure:
-
Sample Preparation:
-
Transport the tendon biopsy to the laboratory in cell culture medium.
-
Wash the sample three times with sterile PBS.
-
Carefully remove the surrounding paratenon.
-
Mince the tendon into small pieces (approximately 2-3 mm).
-
-
Explant Culture:
-
Place the minced tendon pieces into a petri dish containing 10 mL of cell culture medium.
-
Incubate at 37°C with 5% CO2.
-
Change the culture medium every 2-3 days.
-
-
Cell Migration and Expansion:
-
Monitor the culture for the migration of tenocytes from the tendon explants, which typically begins after 2-4 days.
-
After approximately 3 weeks, when a sufficient number of cells have migrated and formed colonies, transfer the tendon explants to new petri dishes to start a new migration cycle. Up to three migration cycles can be performed.[3]
-
-
Cell Passaging:
-
Once the cells reach 80-90% confluency, remove the culture medium and wash the cells with PBS.
-
Add trypsin-EDTA and incubate for 3-5 minutes to detach the cells.
-
Neutralize the trypsin with culture medium and transfer the cell suspension to a conical tube.
-
Centrifuge the cells, resuspend the pellet in fresh medium, and count the cells using a hemocytometer.
-
Seed the cells into new culture flasks for further expansion.
-
| Parameter | Condition/Value | Notes |
| Culture Medium | DMEM/HAM's F12 | Can be supplemented with FBS and antibiotics |
| Incubation | 37°C, 5% CO2 | Standard cell culture conditions |
| First Cell Migration | 2-4 days | Time for initial cell outgrowth |
| Migration Cycle | ~3 weeks | Duration for each explant culture period |
| Passaging | 80-90% confluency | Standard practice to maintain cell health |
References
- 1. Co-delivery of novel bispecific and trispecific engagers by an amplicon vector augments the therapeutic effect of an HSV-based oncolytic virotherapy - PMC [pmc.ncbi.nlm.nih.gov]
- 2. Tendon-derived stem cells from the long head of the biceps tendon: Inflammation does not affect the regenerative potential - PMC [pmc.ncbi.nlm.nih.gov]
- 3. The long head of the biceps tendon is a suitable cell source for tendon tissue regeneration - PMC [pmc.ncbi.nlm.nih.gov]
Application Notes & Protocols for In Vivo Estrogenicity Assessment Using Transgenic Zebrafish Biosensors
For Researchers, Scientists, and Drug Development Professionals
These application notes provide a comprehensive guide for utilizing transgenic zebrafish biosensor models to assess the estrogenic activity of chemical compounds. This technology offers a powerful in vivo platform for screening potential endocrine-disrupting chemicals (EDCs) and evaluating the estrogenic effects of new drug candidates. The protocols detailed below cover the generation of transgenic animals, experimental procedures for compound exposure, and methods for data acquisition and analysis.
Application Notes
Introduction to Transgenic Estrogen Biosensor Models
Transgenic zebrafish have emerged as a highly effective in vivo model for studying the effects of estrogenic compounds.[1][2] These models typically incorporate a genetic construct containing multiple copies of the estrogen response element (ERE), a DNA sequence that binds to the estrogen receptor (ER) when activated by a ligand.[3][4][5] Downstream of the EREs, a reporter gene, most commonly encoding a fluorescent protein like Green Fluorescent Protein (GFP), is placed.[3][4][6] When an estrogenic compound is introduced, it binds to the ER, which then binds to the EREs in the transgene, inducing the expression of the fluorescent reporter. The resulting fluorescence can be visualized and quantified in the transparent zebrafish embryos and larvae, providing a direct measure of estrogenic activity in a living organism.[1][2]
Key Advantages of the Zebrafish Model
-
In Vivo System: Offers the complexity of a whole-animal system, including metabolic processes, which is crucial for assessing the biological activity of compounds.[1]
-
Optical Transparency: The embryos and larvae are transparent, allowing for real-time, non-invasive imaging of fluorescent reporter expression in various tissues.[4]
-
High-Throughput Screening: The small size of zebrafish embryos, their rapid development, and the ability to handle them in multi-well plates make them suitable for high-throughput screening of compound libraries.[6]
-
Sensitivity: Advanced genetic engineering techniques, such as the use of the Gal4ff-UAS system, can enhance the sensitivity of these biosensors, allowing for the detection of estrogenic compounds at environmentally relevant concentrations.[3][4]
-
Conservation of Signaling Pathways: The estrogen signaling pathways in zebrafish are highly homologous to those in humans, making them a relevant model for predicting potential effects in mammals.[7]
Applications in Research and Drug Development
-
Endocrine Disruptor Screening: A primary application is the screening of environmental chemicals, industrial byproducts, and consumer products for estrogenic activity.[1][2]
-
Pharmaceutical Profiling: New drug candidates can be assessed for off-target estrogenic or anti-estrogenic effects early in the development pipeline.
-
Mechanistic Studies: These models can be used to investigate the tissue-specific and temporal dynamics of estrogen signaling in response to different compounds.[7]
-
Dose-Response Analysis: The quantitative nature of the fluorescent reporter output allows for the determination of dose-response relationships and the calculation of potency for different estrogenic compounds.[6][8]
Experimental Protocols
Protocol 1: Generation of Transgenic Estrogen-Responsive Zebrafish
This protocol describes a general method for creating transgenic zebrafish using plasmid microinjection. A common approach involves a two-component system: an "enhancer trap" vector containing the EREs and a Gal4ff transcription factor, and a "reporter" vector with a UAS promoter driving GFP expression.[3][4][5]
Materials:
-
pBR Tol2-3ERE-Gal4ff plasmid
-
UAS-GFP reporter plasmid
-
Transposase mRNA
-
Microinjection apparatus (micromanipulator, microinjector, pulled glass capillaries)
-
Zebrafish breeding pairs
-
Embryo collection dishes
-
Stereomicroscope
Procedure:
-
Prepare Injection Mix: Prepare an injection mix containing the pBR Tol2-3ERE-Gal4ff plasmid (e.g., 18 ng/µL) and transposase mRNA (e.g., 36 ng/µL) in nuclease-free water.[3]
-
Zebrafish Breeding and Egg Collection: Set up breeding tanks with adult zebrafish. Collect freshly fertilized eggs shortly after the lights turn on.
-
Microinjection: Using a stereomicroscope and microinjection apparatus, inject the plasmid/mRNA mix into the cytoplasm of one-cell stage zebrafish embryos.
-
Raise Founder Fish (F0): Raise the injected embryos to adulthood. These are the founder (F0) generation.
-
Screen for Germline Transmission: Outcross the F0 founder fish with wild-type fish.
-
Identify Transgenic Progeny (F1): Collect the eggs from the outcross and expose them to a known estrogenic compound, such as 100 ng/L 17α-ethinylestradiol (EE2), for approximately 3 days.[3]
-
Select GFP-Positive Embryos: Screen the F1 embryos for GFP expression using a fluorescence microscope. GFP-positive embryos indicate successful germline transmission of the transgene.
-
Establish Stable Transgenic Lines: Raise the GFP-positive F1 embryos to adulthood. Subsequent generations can be screened to establish stable transgenic lines.
Protocol 2: Exposure of Zebrafish Embryos to Test Compounds
This protocol details the procedure for exposing transgenic zebrafish embryos to chemical compounds to assess their estrogenic activity.
Materials:
-
Transgenic estrogen-responsive zebrafish embryos
-
Multi-well plates (e.g., 24-well or 96-well)
-
Test compounds and a known estrogen (e.g., 17β-estradiol, E2) as a positive control.
-
Solvent (e.g., DMSO), if required for dissolving compounds.
-
Embryo medium (e.g., E3 medium)
-
Incubator set to 28.5 °C
Procedure:
-
Prepare Test Solutions: Prepare stock solutions of the test compounds and the positive control (E2) in a suitable solvent. Create a dilution series of each compound in embryo medium. The final solvent concentration should be kept low (e.g., <0.01%) to avoid toxicity.[9]
-
Embryo Collection and Staging: Collect healthy, fertilized embryos and stage them under a stereomicroscope.
-
Dechorionation (Optional but Recommended): For early exposure, embryos can be dechorionated enzymatically or manually to increase compound uptake.[8]
-
Exposure Setup: Place one embryo per well in a multi-well plate containing the test solutions. Include a vehicle control (embryo medium with solvent) and a positive control group.
-
Incubation: Incubate the plates at 28.5 °C. The duration of exposure can vary depending on the experimental design (e.g., from a few hours to several days).[6][8]
-
Medium Refreshment: For longer exposures, it is advisable to refresh the test solutions every 24-48 hours.[9]
Protocol 3: In Vivo Imaging and Quantification of GFP Expression
This protocol describes how to image and quantify the fluorescent reporter signal in live zebrafish larvae.
Materials:
-
Exposed zebrafish larvae
-
Anesthetic (e.g., tricaine methanesulfonate, MS-222)
-
Mounting medium (e.g., low-melting-point agarose)
-
Microscope slides with depressions or imaging dishes
-
Fluorescence microscope (e.g., confocal or epifluorescence) with a camera
-
Image analysis software (e.g., ImageJ/Fiji)
Procedure:
-
Anesthetize Larvae: Anesthetize the larvae in a solution of MS-222 in embryo medium.
-
Mount Larvae: Carefully mount the anesthetized larvae in a drop of low-melting-point agarose on a microscope slide or in an imaging dish. Position the larvae for optimal viewing of the tissues of interest (e.g., lateral or dorsal view).
-
Image Acquisition: Acquire fluorescent and brightfield images using the fluorescence microscope. Use consistent settings (e.g., exposure time, gain) across all experimental groups to ensure comparability.
-
Qualitative Analysis: Visually inspect the images to determine the presence and location of GFP expression in different tissues (e.g., liver, heart, brain).[3][4]
-
Quantitative Analysis:
-
Percentage of Responders: Count the number of larvae exhibiting GFP expression in a specific tissue (e.g., liver) for each treatment group and express this as a percentage of the total number of larvae in that group.[6][8]
-
Fluorescence Intensity/Area: Use image analysis software to measure the area and/or mean fluorescence intensity of the GFP signal in a defined region of interest (ROI), such as the liver.[6][8]
-
-
Data Analysis: Plot the quantitative data (e.g., percentage of positive larvae, fluorescence intensity) against the compound concentration to generate dose-response curves.
Quantitative Data Summary
The following tables summarize representative dose-response data for known estrogenic compounds in transgenic zebrafish biosensor models.
Table 1: Dose-Response of 17β-Estradiol (E2) on Hepatic EGFP Expression in tg[vtg1:EGFP] Zebrafish Larvae [6][8]
| E2 Concentration (nM) | Percentage of Larvae with Hepatic EGFP Expression (at 6 dpf) |
| 0 (Control) | 0% |
| 1 | ~5% |
| 2.5 | ~20% |
| 5 | ~80% |
| 25 | ~95% |
| 125 | 100% |
| 625 | 100% |
Table 2: Dose-Response of Bisphenol A (BPA) on Hepatic EGFP Expression in tg[vtg1:EGFP] Zebrafish Larvae [6][8]
| BPA Concentration (µM) | Percentage of Larvae with Hepatic EGFP Expression (at 5 dpf) |
| 0 (Control) | 0% |
| 5 | ~5% |
| 10 | ~25% |
| 20 | ~60% |
| 30 | ~75% |
Signaling Pathway and Experimental Workflow Diagrams
Caption: Genomic estrogen signaling pathway.
Caption: Non-genomic estrogen signaling pathway.
Caption: Experimental workflow for estrogenicity assessment.
References
- 1. Use of Reporter Genes to Analyze Estrogen Response: The Transgenic Zebrafish Model | Springer Nature Experiments [experiments.springernature.com]
- 2. researchgate.net [researchgate.net]
- 3. Biosensor Zebrafish Provide New Insights into Potential Health Effects of Environmental Estrogens - PMC [pmc.ncbi.nlm.nih.gov]
- 4. researchgate.net [researchgate.net]
- 5. Item - Development of ERE-Transgenic Zebrafish for Studying Health Effects of Environmental Oestrogens - University of Exeter - Figshare [ore.exeter.ac.uk]
- 6. Fluorescent Reporter Zebrafish Line for Estrogenic Compound Screening Generated Using a CRISPR/Cas9-Mediated Knock-in System - PMC [pmc.ncbi.nlm.nih.gov]
- 7. Frontiers | Application of Transgenic Zebrafish Models for Studying the Effects of Estrogenic Endocrine Disrupting Chemicals on Embryonic Brain Development [frontiersin.org]
- 8. Fluorescent Reporter Zebrafish Line for Estrogenic Compound Screening Generated Using a CRISPR/Cas9-Mediated Knock-in System - PubMed [pubmed.ncbi.nlm.nih.gov]
- 9. mdpi.com [mdpi.com]
Application Notes and Protocols for Bicep Dosage Calculation in In Vivo Studies
For Researchers, Scientists, and Drug Development Professionals
These application notes provide a comprehensive guide for the dosage calculation and in vivo evaluation of "Bicep," a hypothetical small molecule inhibitor targeting the PI3K/Akt/mTOR signaling pathway. The protocols outlined below are intended for preclinical cancer research in murine models.
Introduction to this compound
This compound is a potent and selective small molecule inhibitor of the PI3K/Akt/mTOR signaling pathway, a critical cellular cascade that is frequently dysregulated in various human cancers. By targeting this pathway, this compound aims to inhibit tumor cell growth, proliferation, and survival. These notes will guide researchers through the essential steps of determining the appropriate dosage of this compound for in vivo studies, from initial in vitro characterization to efficacy testing in xenograft models.
In Vitro Characterization of this compound
Prior to in vivo studies, it is crucial to determine the in vitro potency of this compound in relevant cancer cell lines. This is typically achieved by measuring the half-maximal inhibitory concentration (IC50).
Table 1: In Vitro IC50 of this compound in Human Cancer Cell Lines
| Cell Line | Cancer Type | IC50 (nM) |
| MCF-7 | Breast Cancer | 50 |
| PC-3 | Prostate Cancer | 120 |
| A549 | Lung Cancer | 250 |
| U-87 MG | Glioblastoma | 85 |
Protocol 1: In Vitro Cell Viability Assay (MTT Assay)
-
Cell Seeding: Plate cancer cells in 96-well plates at a density of 5,000-10,000 cells per well and allow them to adhere overnight.
-
Drug Treatment: Prepare serial dilutions of this compound in culture medium and treat the cells for 72 hours.
-
MTT Addition: Add MTT reagent (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) to each well and incubate for 4 hours to allow the formation of formazan crystals.
-
Solubilization: Add solubilization solution (e.g., DMSO) to dissolve the formazan crystals.
-
Absorbance Reading: Measure the absorbance at 570 nm using a microplate reader.
-
IC50 Calculation: Plot the percentage of cell viability against the log concentration of this compound to determine the IC50 value.
In Vivo Maximum Tolerated Dose (MTD) Study
The MTD study is essential to determine the highest dose of this compound that can be administered without causing unacceptable toxicity.
Table 2: Example MTD Study Design for this compound in Mice
| Group | Dose (mg/kg) | Administration Route | Dosing Schedule | Number of Animals |
| 1 | Vehicle | Oral Gavage | Daily for 14 days | 5 |
| 2 | 10 | Oral Gavage | Daily for 14 days | 5 |
| 3 | 30 | Oral Gavage | Daily for 14 days | 5 |
| 4 | 60 | Oral Gavage | Daily for 14 days | 5 |
| 5 | 100 | Oral Gavage | Daily for 14 days | 5 |
Protocol 2: MTD Study in Nude Mice
-
Animal Acclimation: Acclimate healthy female nude mice (6-8 weeks old) for at least one week.
-
Group Assignment: Randomly assign mice to treatment groups.
-
Drug Administration: Prepare this compound in a suitable vehicle (e.g., 0.5% methylcellulose) and administer daily via oral gavage for 14 consecutive days.
-
Monitoring: Monitor the animals daily for clinical signs of toxicity, including changes in behavior, appearance, and body weight. Body weight should be recorded at least three times a week.
-
Endpoint: The MTD is defined as the highest dose that does not result in more than 15-20% body weight loss or any signs of severe toxicity.
In Vivo Efficacy Study in a Xenograft Model
Once the MTD is established, the anti-tumor efficacy of this compound can be evaluated in a tumor xenograft model.
Table 3: Example Efficacy Study Design for this compound
| Group | Treatment | Dose (mg/kg) | Dosing Schedule | Number of Animals |
| 1 | Vehicle | - | Daily for 21 days | 10 |
| 2 | This compound | 30 | Daily for 21 days | 10 |
| 3 | This compound | 60 | Daily for 21 days | 10 |
Protocol 3: Xenograft Tumor Efficacy Study
-
Tumor Cell Implantation: Subcutaneously implant human cancer cells (e.g., MCF-7) into the flank of nude mice.
-
Tumor Growth: Allow the tumors to grow to a palpable size (e.g., 100-150 mm³).
-
Randomization: Randomize the tumor-bearing mice into treatment groups.
-
Treatment: Administer this compound or vehicle as per the study design.
-
Tumor Measurement: Measure tumor volume using calipers at least twice a week. Tumor volume can be calculated using the formula: (Length x Width²)/2.
-
Endpoint: The study is typically terminated when the tumors in the vehicle group reach a predetermined size. Tumor growth inhibition (TGI) is calculated for each treatment group.
Visualizations
Signaling Pathway of this compound
Caption: this compound inhibits the PI3K/Akt/mTOR signaling pathway.
Experimental Workflow for In Vivo Studies
Caption: Workflow for preclinical in vivo evaluation of this compound.
Dose Selection Logic
Caption: Logic for selecting doses for efficacy studies.
Application Notes and Protocols: Preparation and Storage of Protein Solutions
For Researchers, Scientists, and Drug Development Professionals
This document provides detailed guidelines and protocols for the preparation and storage of protein solutions to ensure their stability and functionality for research and drug development applications. Proper handling and storage are critical to prevent degradation, aggregation, and loss of biological activity.
General Guidelines for Protein Solution Preparation
The initial preparation of a protein solution is a critical step that dictates its short-term and long-term stability. The primary goal is to solubilize the protein in a buffer system that maintains its native conformation and activity.
Key Considerations:
-
Buffer System: The choice of buffer is crucial for maintaining a stable pH. Common biological buffers include phosphate-buffered saline (PBS), Tris-HCl, and HEPES. The optimal pH for a protein is typically at or near its physiological pH, but may need to be optimized to prevent aggregation.
-
Protein Concentration: Dilute protein solutions (<1 mg/ml) may be more susceptible to adsorption to storage vessel surfaces. It is often advisable to store proteins at a higher concentration and dilute as needed. To mitigate binding to surfaces, adding a "filler" protein like Bovine Serum Albumin (BSA) can be beneficial.[1]
-
Additives: Various additives can be included in the buffer to enhance protein stability:
-
Reducing Agents: To prevent oxidation of cysteine residues, reducing agents like dithiothreitol (DTT) or 2-mercaptoethanol (2-ME) can be added at final concentrations of 1-5 mM.[2]
-
Protease Inhibitors: To prevent proteolytic degradation, a cocktail of protease inhibitors (e.g., EDTA, PMSF) should be added, especially during the initial extraction and purification stages.[1]
-
Antimicrobial Agents: For short-term storage at 4°C, including an antimicrobial agent such as sodium azide (0.05% w/v) or thimerosal (0.01% w/v) can prevent microbial growth.[1]
-
Protein Solution Storage
The appropriate storage condition depends on the required shelf life and the nature of the protein.
Table 1: Comparison of Protein Storage Conditions
| Storage Condition | Typical Shelf Life | Requires Sterile Conditions/Antibacterial Agent | Suitability for Repeated Use | Key Considerations |
| Solution at 4°C | Days to Weeks | Yes | Many times | Convenient for frequent use, but higher risk of microbial growth and proteolysis.[2][3] |
| Solution with Cryoprotectant at -20°C | Up to 1 Year | Usually | Many times | Cryoprotectants (25-50% glycerol or ethylene glycol) prevent ice crystal formation.[1][2][3] |
| Frozen at -80°C or in Liquid Nitrogen | Years | No | Single-use aliquots recommended | Ideal for long-term storage; repeated freeze-thaw cycles must be avoided as they can degrade proteins.[1][2][3] |
| Lyophilized (Freeze-Dried) | Years | No | Reconstitution needed before each use | Offers excellent long-term stability, but the lyophilization process itself can damage some proteins.[1][2][3] |
Experimental Protocols
Protocol 1: Preparation of a Stock Protein Solution
Objective: To prepare a concentrated, stable stock solution of a purified protein.
Materials:
-
Purified protein (lyophilized powder or from a purification column)
-
Sterile, high-purity water
-
Sterile buffer components (e.g., Tris base, HCl, NaCl, EDTA)
-
Glycerol (optional, for -20°C storage)
-
Protease inhibitor cocktail
-
Sterile polypropylene microcentrifuge tubes
-
Calibrated pipettes and sterile tips
-
pH meter
-
Spectrophotometer
Procedure:
-
Buffer Preparation:
-
Prepare the desired buffer (e.g., 50 mM Tris-HCl, 150 mM NaCl, 1 mM EDTA, pH 7.4).
-
Filter the buffer through a 0.22 µm filter to ensure sterility.
-
-
Protein Solubilization:
-
If starting with a lyophilized powder, allow the vial to equilibrate to room temperature before opening to prevent condensation.[4]
-
Gently add the sterile buffer to the protein powder. To aid dissolution, gently swirl or pipette the solution up and down. Avoid vigorous shaking or vortexing, which can cause denaturation and aggregation.
-
-
Concentration Determination:
-
Measure the protein concentration using a spectrophotometer (e.g., at 280 nm) or a colorimetric assay (e.g., Bradford or BCA assay).
-
-
Addition of Stabilizers (if required):
-
Add protease inhibitors to the freshly prepared solution.
-
If preparing for storage at -20°C, add sterile glycerol to a final concentration of 25-50% (v/v) and mix gently.[1]
-
-
Aliquoting:
-
Storage:
-
Label the aliquots clearly with the protein name, concentration, date, and buffer composition.
-
Store the aliquots at the appropriate temperature as determined by the desired storage duration (see Table 1).
-
Protocol 2: Assessment of Protein Stability by Cycloheximide Chase Assay
Objective: To determine the in-cell half-life of a protein by inhibiting protein synthesis and observing its degradation over time.
Materials:
-
Cultured cells expressing the protein of interest
-
Complete cell culture medium
-
Cycloheximide (CHX) stock solution (e.g., 100 mg/mL in DMSO)
-
Phosphate-Buffered Saline (PBS)
-
Cell lysis buffer (e.g., RIPA buffer) with protease inhibitors
-
Apparatus for SDS-PAGE and Western blotting
-
Primary antibody specific to the protein of interest
-
Secondary antibody (e.g., HRP-conjugated)
-
Chemiluminescence substrate
Procedure:
-
Cell Culture: Plate cells at an appropriate density and allow them to adhere and grow for 24-48 hours.
-
Cycloheximide Treatment:
-
Treat the cells with cycloheximide at a final concentration that effectively inhibits protein synthesis in the specific cell line (e.g., 10-100 µg/mL).[5]
-
This marks the "time zero" (t=0) point.
-
-
Time Course Collection:
-
Harvest cells at various time points after CHX addition (e.g., 0, 2, 4, 6, 8, 12, 24 hours).
-
To harvest, wash the cells with ice-cold PBS and then add lysis buffer.
-
-
Protein Quantification and Analysis:
-
Collect the cell lysates and determine the total protein concentration for each time point.
-
Normalize the samples to ensure equal protein loading for SDS-PAGE.
-
-
Western Blotting:
-
Separate the protein lysates by SDS-PAGE and transfer them to a membrane.
-
Probe the membrane with the primary antibody against the protein of interest, followed by the HRP-conjugated secondary antibody.
-
-
Data Analysis:
-
Detect the protein bands using a chemiluminescence imaging system.
-
Quantify the band intensity for each time point.
-
Plot the band intensity versus time and fit the data to a one-phase decay curve to calculate the protein's half-life.
-
Visualizations
Experimental Workflow for Protein Solution Preparation and Storage
Caption: Workflow for Protein Solution Preparation and Storage
Decision Tree for Protein Storage Method Selection
Caption: Decision Tree for Selecting a Protein Storage Method
References
Application of BICeps in Molecular Biology Assays: Application Notes and Protocols
For Researchers, Scientists, and Drug Development Professionals
Introduction
In the realm of molecular biology and drug development, understanding the conformational dynamics of proteins and other biomolecules is paramount to deciphering their function and interactions. While computational methods like molecular dynamics (MD) simulations provide valuable insights into these dynamics, they are often limited by the accuracy of the underlying force fields. Experimental techniques, such as Nuclear Magnetic Resonance (NMR) spectroscopy, offer exquisitely sensitive measurements of molecular structure and dynamics, but often provide sparse data that is challenging to interpret on its own.
To bridge this gap, the Bayesian Inference of Conformational Populations (BICePs) algorithm has emerged as a powerful tool. BICeps is a computational method that integrates theoretical predictions from molecular simulations with experimental data to produce a more accurate and experimentally-consistent conformational ensemble of a molecule.[1][2][3] This is achieved through a rigorous Bayesian statistical framework that reweights the populations of different conformational states from a simulation to better match the experimental observables.[1][2]
This document provides detailed application notes and protocols for utilizing BICePs in conjunction with molecular biology assays, with a focus on leveraging NMR spectroscopy data.
Core Concepts of BICePs
The fundamental principle of BICePs is to refine a theoretical model of a molecule's conformational landscape by incorporating experimental data. The key inputs for a BICePs analysis are:
-
A theoretical conformational ensemble: This is typically generated from a molecular dynamics (MD) simulation, which provides a set of discrete conformational states and their predicted populations based on a force field.[1][4]
-
Experimental observables: These are quantitative measurements from molecular biology assays that are sensitive to the molecule's conformation. BICePs is particularly well-suited for use with NMR-derived data, including:
The output of a BICePs calculation is a set of reweighted conformational populations that represent a more accurate description of the molecule's behavior in solution.[1] A key feature of BICePs is the calculation of a BICePs score , a metric that quantifies how well a given theoretical model (e.g., a force field) agrees with the experimental data, allowing for objective model selection.[2][3]
Application: Refining the Conformational Ensemble of a Peptide
A primary application of BICePs is to refine the structural ensembles of peptides and proteins. By combining MD simulations with experimental NMR data, researchers can obtain a more accurate picture of the dynamic behavior of these molecules, which is crucial for understanding their biological function, including protein-protein interactions and ligand binding.
Key Experiments and Methodologies
The following sections outline the experimental and computational protocols for a typical BICePs-based analysis of a peptide's conformational ensemble.
1. Experimental Protocol: NMR Data Acquisition
High-quality NMR data is crucial for a successful BICePs analysis. The following protocols are for the acquisition of common NMR restraints for a peptide sample.
a) Sample Preparation:
-
Dissolve the isotopically labeled (e.g., ¹⁵N, ¹³C) peptide in a suitable buffer (e.g., 20 mM sodium phosphate, 100 mM NaCl, pH 6.5) to a final concentration of 0.5-1.0 mM.
-
Add 5-10% D₂O to the sample for the lock signal.
b) Nuclear Overhauser Effect (NOE) Data:
-
Experiment: 2D ¹H-¹H NOESY (Nuclear Overhauser Effect Spectroscopy).
-
Purpose: To measure through-space proton-proton distances (typically < 6 Å).[6]
-
Protocol:
-
Set the spectrometer to the appropriate temperature (e.g., 298 K).
-
Acquire a series of 2D NOESY spectra with varying mixing times (e.g., 50, 100, 150, 200 ms).
-
Process the spectra using software such as NMRPipe.
-
Integrate the cross-peak volumes to determine NOE intensities.
-
Convert NOE intensities to distance restraints using a calibration protocol.
-
c) J-Coupling Constants:
-
Experiment: 3D HNHA (for ³J(HN-Hα) couplings).
-
Purpose: To measure through-bond scalar couplings, which are related to dihedral angles via Karplus relationships.[7]
-
Protocol:
-
Acquire a 3D HNHA spectrum.
-
Process the spectrum and measure the splitting of cross-peaks to determine the coupling constants.
-
d) Chemical Shift Data:
-
Experiment: 2D ¹H-¹⁵N HSQC (Heteronuclear Single Quantum Coherence).
-
Purpose: To obtain the chemical shifts of backbone amide protons and nitrogens.[8]
-
Protocol:
-
Acquire a high-resolution 2D ¹H-¹⁵N HSQC spectrum.
-
Process the spectrum and pick the peak positions to determine the chemical shifts for each assigned residue.
-
2. Computational Protocol: BICePs Workflow
The following protocol outlines the steps for performing a BICePs analysis using the acquired NMR data and a pre-existing molecular dynamics simulation trajectory of the peptide.
a) Preparation of Input Files:
-
Conformational Ensemble:
-
Cluster the MD trajectory to obtain a set of representative conformational states.
-
For each state, calculate the "forward model" for each experimental observable. The forward model is a theoretical prediction of the observable for a given conformation.[1]
-
Create a file containing the forward model predictions for each state and each restraint.
-
-
Experimental Restraints File:
-
Create a formatted text file containing the experimentally measured values for each restraint (NOE distances, J-couplings, chemical shifts) and their corresponding uncertainties.
-
b) Running the BICePs Calculation:
The BICePs software is a Python package.[9] The general workflow involves the following steps:
-
Initialization: Import the biceps library and load the experimental data and forward model predictions into a biceps.Preparation object.[1]
-
Ensemble Setup: Create a biceps.Ensemble object, which links the conformational states with the experimental restraints.[5]
-
Posterior Sampling: Use the biceps.PosteriorSampler to perform a Markov Chain Monte Carlo (MCMC) simulation to sample the posterior probability distribution of the conformational populations and nuisance parameters (which account for experimental and forward model uncertainties).[1]
-
Analysis: Use the biceps.Analysis class to analyze the results of the MCMC simulation, including calculating the reweighted conformational populations and the BICePs score.[5]
c) Visualization of the BICePs Workflow:
Caption: Workflow for BICePs analysis.
Data Presentation
The results of a BICePs analysis can be summarized in tables for easy comparison and interpretation.
Table 1: Comparison of Conformational Populations Before and After BICePs Reweighting
| Conformational Cluster | Initial Population (from MD) | Reweighted Population (BICePs) |
| 1 | 0.25 | 0.45 |
| 2 | 0.30 | 0.20 |
| 3 | 0.15 | 0.10 |
| 4 | 0.10 | 0.15 |
| 5 | 0.20 | 0.10 |
Table 2: BICePs Score for Different Force Fields
| Force Field | BICePs Score |
| AMBER99SB-ILDN | -150.2 |
| CHARMM36m | -125.8 |
| GROMOS54a7 | -180.5 |
A lower BICePs score indicates better agreement between the simulation and experimental data.
Signaling Pathway and Logical Relationship Visualization
BICePs can be used to study how the conformational dynamics of a protein are altered upon binding to a signaling partner. The reweighted conformational ensembles can provide insights into the allosteric mechanisms that govern signal transduction.
Caption: Ligand binding shifts conformational equilibrium.
Conclusion
The BICePs algorithm provides a robust and statistically rigorous framework for integrating computational and experimental data to refine our understanding of molecular dynamics. For researchers in molecular biology and drug development, BICePs offers a powerful tool to generate more accurate models of protein conformational ensembles, leading to deeper insights into protein function, protein-protein interactions, and the mechanisms of drug action. By following the detailed protocols outlined in this document, scientists can effectively apply BICePs to their own research, ultimately accelerating the pace of discovery.
References
- 1. BICePs v2.0: Software for Ensemble Reweighting using Bayesian Inference of Conformational Populations - PMC [pmc.ncbi.nlm.nih.gov]
- 2. Reconciling Simulations and Experiments With BICePs: A Review - PMC [pmc.ncbi.nlm.nih.gov]
- 3. Model Selection Using BICePs: A Bayesian Approach for Force Field Validation and Parameterization - PMC [pmc.ncbi.nlm.nih.gov]
- 4. Frontiers | Reconciling Simulations and Experiments With BICePs: A Review [frontiersin.org]
- 5. BICePs - Bayesian Inference of Conformational Populations — BICePs 2.0 documentation [biceps.readthedocs.io]
- 6. pubs.acs.org [pubs.acs.org]
- 7. Protein NMR. J(HN-HA) Coupling Constants [imserc.northwestern.edu]
- 8. protein-nmr.org.uk [protein-nmr.org.uk]
- 9. pubs.acs.org [pubs.acs.org]
Application Notes and Protocols for High-Throughput Screening Assays
For Researchers, Scientists, and Drug Development Professionals
These application notes provide detailed methodologies for high-throughput screening (HTS) of two innovative therapeutic modalities: bicyclic peptides and bispecific antibodies. The protocols outlined below are designed to guide researchers through the complex workflows of hit identification and characterization.
Part 1: High-Throughput Screening of Bicyclic Peptides
Bicyclic peptides are a novel class of therapeutics that combine the affinity and specificity of antibodies with the manufacturing and tissue penetration advantages of small molecules. High-throughput screening is essential for identifying lead candidates from vast combinatorial libraries. The most common method for discovering bicyclic peptides is through phage display.
Signaling Pathway of a Bicyclic Peptide Modulator
Bicyclic peptides can be designed to interact with a wide range of targets, including cell surface receptors, enzymes, and protein-protein interactions. The following diagram illustrates a generic signaling pathway where a bicyclic peptide acts as an antagonist to a receptor tyrosine kinase (RTK).
Caption: Bicyclic peptide antagonizing an RTK signaling pathway.
Experimental Workflow: Phage Display Screening for Bicyclic Peptides
The following workflow outlines the key steps in a typical phage display campaign to identify bicyclic peptides that bind to a specific target protein.
Caption: Phage display workflow for bicyclic peptide discovery.
Protocol: Phage Display Panning for Bicyclic Peptides
This protocol describes a single round of affinity selection (panning) against an immobilized protein target.
Materials:
-
Phage library displaying bicyclic peptides
-
Target protein, biotinylated
-
Streptavidin-coated magnetic beads
-
Panning buffer (e.g., PBS with 0.1% Tween-20 and 1% BSA)
-
Wash buffer (e.g., PBS with 0.1% Tween-20)
-
Elution buffer (e.g., 100 mM glycine-HCl, pH 2.2)
-
Neutralization buffer (e.g., 1 M Tris-HCl, pH 9.1)
-
Log-phase E. coli culture
-
LB agar plates
Procedure:
-
Bead Preparation: Resuspend streptavidin-coated magnetic beads in panning buffer.
-
Target Immobilization: Incubate the beads with the biotinylated target protein for 1 hour at room temperature with gentle rotation.
-
Blocking: Wash the beads three times with panning buffer to remove unbound target protein. Block the beads with panning buffer for 30 minutes.
-
Phage Binding: Add the bicyclic peptide phage library to the blocked beads. Incubate for 2 hours at room temperature with gentle rotation.
-
Washing:
-
Separate the beads using a magnetic stand and discard the supernatant.
-
Wash the beads 5-10 times with wash buffer. Increase the stringency of washing in subsequent panning rounds.
-
-
Elution:
-
Resuspend the beads in elution buffer and incubate for 10 minutes to release the bound phage.
-
Separate the beads and transfer the supernatant containing the eluted phage to a new tube.
-
Neutralize the eluted phage with neutralization buffer.
-
-
Amplification:
-
Infect a log-phase E. coli culture with the neutralized, eluted phage.
-
Plate the infected bacteria on LB agar plates and incubate overnight at 37°C.
-
Harvest the amplified phage for the next round of panning.
-
Quantitative Data: Bicyclic Peptide Screening
The following table summarizes representative data from a hypothetical screening campaign to identify inhibitors of a target protein.
| Parameter | Round 1 | Round 2 | Round 3 | Round 4 |
| Input Phage Titer (pfu/ml) | 1 x 10¹² | 1 x 10¹² | 1 x 10¹² | 1 x 10¹² |
| Output Phage Titer (pfu/ml) | 1 x 10⁵ | 2 x 10⁶ | 5 x 10⁷ | 8 x 10⁸ |
| Enrichment Factor | - | 20 | 25 | 16 |
| Number of Unique Hits | >1000 | 250 | 45 | 12 |
| Affinity of Top Hit (nM) | Not Determined | 500 | 85 | 15 |
Part 2: High-Throughput Screening of Bispecific Antibodies
Bispecific antibodies (BsAbs) can simultaneously bind to two different epitopes, enabling novel mechanisms of action such as redirecting immune cells to tumor cells. HTS is critical for identifying BsAb candidates with optimal functional activity from large panels of parental antibodies.
Logical Relationship: Bispecific T-Cell Engager (BiTE) Mechanism
This diagram illustrates the mechanism of action for a BiTE, a common type of BsAb that engages T-cells to kill tumor cells.
Caption: Mechanism of action for a bispecific T-cell engager.
Experimental Workflow: Combinatorial Screening of Bispecific Antibodies
This workflow describes a high-throughput approach to screen a matrix of parental antibodies to identify the most potent bispecific combinations.
Caption: Combinatorial screening workflow for bispecific antibodies.
Protocol: ELISA-Based Dual-Target Bridging Assay
This protocol is for a common ELISA format used to confirm that a BsAb can simultaneously bind to both of its targets.
Materials:
-
96-well microplates
-
Target A protein
-
Target B protein, biotinylated
-
Bispecific antibody samples and controls
-
Coating buffer (e.g., carbonate-bicarbonate buffer, pH 9.6)
-
Blocking buffer (e.g., PBS with 1% BSA)
-
Wash buffer (e.g., PBS with 0.05% Tween-20)
-
Streptavidin-HRP
-
TMB substrate
-
Stop solution (e.g., 2 M H₂SO₄)
-
Plate reader
Procedure:
-
Coating: Coat the wells of a 96-well plate with Target A protein (2 µg/mL in coating buffer) and incubate overnight at 4°C.
-
Washing & Blocking:
-
Wash the plate three times with wash buffer.
-
Block the plate with blocking buffer for 1 hour at 37°C.
-
-
BsAb Binding:
-
Wash the plate three times.
-
Add serial dilutions of the bispecific antibody to the wells and incubate for 1 hour at 37°C.
-
-
Biotinylated Target Binding:
-
Wash the plate three times.
-
Add biotinylated Target B protein (2 µg/mL in blocking buffer) and incubate for 1 hour at 37°C.
-
-
Detection:
-
Wash the plate three times.
-
Add Streptavidin-HRP (diluted 1:1000 in blocking buffer) and incubate for 1 hour at 37°C.
-
-
Development & Reading:
-
Wash the plate three times.
-
Add TMB substrate and incubate for 10-15 minutes at room temperature.
-
Stop the reaction with stop solution.
-
Read the absorbance at 450 nm using a plate reader.
-
Quantitative Data: Bispecific Antibody Functional Screen
The following table shows representative data from a high-throughput screen of different BsAb combinations targeting Tumor Antigen X and CD3 for T-cell mediated tumor cell killing.
| BsAb Combination | Parental Ab A (Anti-Tumor Ag) | Parental Ab B (Anti-CD3) | % Tumor Cell Lysis (at 1 nM) | EC₅₀ (pM) |
| 1 | Clone A1 | Clone B1 | 75% | 150 |
| 2 | Clone A1 | Clone B2 | 82% | 95 |
| 3 | Clone A2 | Clone B1 | 60% | 320 |
| 4 | Clone A2 | Clone B2 | 68% | 250 |
| Monospecific Control | Clone A1 | - | <5% | N/A |
| Monospecific Control | - | Clone B2 | <5% | N/A |
Application Notes and Protocols for Intracellular Delivery Methods in Laboratory Research
For Researchers, Scientists, and Drug Development Professionals
Introduction
The delivery of therapeutic and research molecules into living cells is a critical process in a wide range of laboratory and clinical applications, from basic research to drug development. The cell membrane presents a formidable barrier to the entry of many macromolecules, including proteins, peptides, and nucleic acids. This document provides an overview and detailed protocols for several key methods used to overcome this barrier, with a focus on peptide-based delivery and physical transfection methods. While the term "Bicep delivery" is not a standard nomenclature in the field, it is interpreted here to encompass methods involving biological molecules (like peptides) and physical forces for intracellular penetration, such as Cell-Penetrating Peptides (CPPs) and Biolistics.
I. Cell-Penetrating Peptide (CPP)-Mediated Delivery
Cell-Penetrating Peptides (CPPs) are short peptides, typically fewer than 30 amino acids long, that can translocate across cellular membranes and facilitate the intracellular delivery of various molecular cargoes.[1][2] They represent a versatile and efficient method for transporting molecules that would otherwise be membrane-impermeable.[3]
Mechanism of Action: CPPs utilize various mechanisms to enter cells, which can be broadly categorized into direct membrane translocation and endocytosis-dependent pathways.[4]
-
Direct Translocation: Some CPPs can directly penetrate the plasma membrane, a process that is often initiated by electrostatic interactions with negatively charged components of the cell surface.[1]
-
Endocytosis: Many CPPs and their cargo are internalized through various endocytic pathways.[4] A key challenge is the subsequent escape from endosomes to release the cargo into the cytoplasm.[1]
Advantages:
-
High efficiency for a variety of cargo types (small molecules, proteins, nucleic acids).[5]
-
Low cytotoxicity at effective concentrations.[5]
-
Amenable to chemical modification and synthesis.[5]
Limitations:
-
Lack of cell-type specificity can be a concern for targeted therapies.[3]
-
Susceptibility to proteolytic degradation in vivo.[2]
-
Potential for endosomal entrapment of the cargo.[2]
Experimental Protocol: CPP-Mediated Delivery of a Fluorescently Labeled Protein
This protocol describes the delivery of a fluorescently labeled protein into cultured mammalian cells using a commercially available CPP.
Materials:
-
Cultured mammalian cells (e.g., HeLa, HEK293)
-
Complete cell culture medium
-
Phosphate-Buffered Saline (PBS)
-
Fluorescently labeled protein (e.g., GFP, RFP)
-
Cell-Penetrating Peptide (e.g., TAT, Penetratin)
-
Serum-free cell culture medium
-
Fluorescence microscope
Procedure:
-
Cell Seeding: The day before the experiment, seed the mammalian cells in a 24-well plate at a density that will result in 70-80% confluency on the day of transfection.
-
Complex Formation:
-
Dilute the fluorescently labeled protein to the desired final concentration in serum-free medium.
-
Dilute the CPP to the desired final concentration in a separate tube of serum-free medium.
-
Add the diluted CPP solution to the diluted protein solution and mix gently by pipetting.
-
Incubate the mixture at room temperature for 30 minutes to allow for the formation of CPP-protein complexes.
-
-
Cell Treatment:
-
Aspirate the culture medium from the cells and wash once with PBS.
-
Add the CPP-protein complex solution to the cells.
-
Incubate the cells at 37°C in a CO2 incubator for 4 hours.
-
-
Post-Incubation:
-
Aspirate the CPP-protein complex solution.
-
Wash the cells three times with PBS to remove extracellular complexes.
-
Add fresh, complete culture medium to the cells.
-
-
Visualization:
-
Observe the cells under a fluorescence microscope to visualize the intracellular delivery of the fluorescent protein.
-
Signaling Pathway for CPP-Mediated Endocytic Uptake
References
- 1. mdpi.com [mdpi.com]
- 2. Cell-Penetrating Peptides as Valuable Tools for Nose-to-Brain Delivery of Biological Drugs - PMC [pmc.ncbi.nlm.nih.gov]
- 3. Smart Cell-Penetrating Peptide-Based Techniques for Intracellular Delivery of Therapeutic Macromolecules - PubMed [pubmed.ncbi.nlm.nih.gov]
- 4. mdpi.com [mdpi.com]
- 5. Applications of cell penetrating peptide-based drug delivery system in immunotherapy - PMC [pmc.ncbi.nlm.nih.gov]
Application Note: Quantifying Binding Immunoglobulin Protein (BiP) in Biological Samples
Audience: Researchers, scientists, and drug development professionals.
Note on Terminology: This document provides protocols for the quantification of the Binding Immunoglobulin Protein (BiP), also known as 78 kDa glucose-regulated protein (GRP78) or HSPA5. It is presumed that the query "Bicep" was a typographical error for the molecular chaperone "BiP," a protein of significant interest in cellular stress pathways and disease.
Introduction
The Binding Immunoglobulin Protein (BiP), also known as GRP78, is a master chaperone protein residing in the endoplasmic reticulum (ER).[1] As a member of the Heat Shock Protein 70 (HSP70) family, BiP is essential for maintaining cellular homeostasis.[2][3] Its canonical functions include aiding in the proper folding and assembly of nascent proteins, preventing the aggregation of misfolded proteins, and targeting irreparable proteins for degradation.[4][5]
BiP is also a central regulator of the Unfolded Protein Response (UPR), a critical signaling network activated by ER stress.[4] Under normal conditions, BiP binds to and inactivates the three main ER stress sensors: PERK, IRE1, and ATF6.[5] Upon accumulation of unfolded proteins, BiP releases these sensors, initiating downstream signaling to restore ER homeostasis or, if the stress is prolonged, trigger apoptosis.[6]
Given its crucial role in proteostasis and cell survival, aberrant BiP expression or function is implicated in numerous diseases, including cancer, neurodegenerative disorders, and metabolic diseases.[2][7] In oncology, elevated BiP levels are often associated with tumor progression, therapeutic resistance, and poor prognosis.[7][8] Consequently, the accurate quantification of BiP in various biological samples—such as serum, plasma, tissue lysates, and cell culture supernatants—is vital for biomarker discovery, diagnostics, and the development of novel therapeutic strategies targeting the UPR pathway.[9][10]
This application note provides detailed protocols for three common methods for BiP quantification: Enzyme-Linked Immunosorbent Assay (ELISA), Western Blotting, and Mass Spectrometry.
Methods for BiP Quantification
Enzyme-Linked Immunosorbent Assay (ELISA)
ELISA is a highly sensitive and high-throughput method ideal for quantifying BiP in liquid samples like serum, plasma, and cell culture supernatants.[11] The sandwich ELISA format is most common, where the target protein is "sandwiched" between a capture antibody coated on a microplate well and a detection antibody, providing high specificity.[12]
Western Blotting (Semi-Quantitative)
Western blotting allows for the semi-quantitative analysis of BiP in cell or tissue lysates. This technique separates proteins by molecular weight, enabling visualization of the ~78 kDa BiP protein.[13] By normalizing the BiP band intensity to a loading control (e.g., β-actin or GAPDH), relative changes in protein expression between samples can be determined.[14]
Mass Spectrometry (MS)
Mass spectrometry offers a highly specific and sensitive platform for absolute protein quantification.[15] In a typical "bottom-up" proteomics workflow, proteins are digested into peptides, which are then analyzed by liquid chromatography-tandem mass spectrometry (LC-MS/MS).[16] By spiking the sample with a known quantity of a stable isotope-labeled synthetic peptide corresponding to a unique BiP peptide, the absolute concentration of the endogenous BiP protein can be precisely determined.[17]
Data Presentation: Typical BiP Concentrations
The concentration of BiP can vary significantly depending on the biological sample, species, and pathological state. The following tables summarize representative quantitative data from published studies.
Table 1: BiP/GRP78 Concentration in Human Clinical Samples
| Sample Type | Condition | Mean Concentration (Range) | Method | Reference(s) |
| Serum | Metabolic Syndrome | 9.15 µg/mL (5.85–16.73 µg/mL) | ELISA | [9] |
| Serum | Healthy Controls | 4.15 µg/mL (2.91–5.76 µg/mL) | ELISA | [9] |
| Serum | Non-Small Cell Lung Cancer (Late-Stage) | 1227 ± 223.6 pg/mL | ELISA | [10] |
| Serum | Non-Small Cell Lung Cancer (Early-Stage) | 326.5 ± 49.77 pg/mL | ELISA | [10] |
| Serum | COVID-19 with Mucormycosis | 374.3 ± 127.3 pg/mL | ELISA | [18] |
| Serum | COVID-19 Controls | 246.4 ± 67.0 pg/mL | ELISA | [18] |
| Serum | Healthy Controls (COVID-19 Study) | 184.8 ± 23.2 pg/mL | ELISA | [18] |
| Bone Marrow Plasma | Multiple Myeloma (Relapsed/Refractory) | 4.0 ng/mL (1.6–7.8 ng/mL) | ELISA | [19] |
Table 2: BiP/GRP78 Concentration in In Vitro Samples
| Sample Type | Condition/Cell Line | Mean Concentration (per 5 µg/mL load) | Method | Reference(s) |
| Cell Extract | HeLa (Tunicamycin-treated) | 7.72 ng/mL | ELISA | |
| Cell Extract | HeLa (Untreated) | 2.19 ng/mL | ELISA |
Experimental Protocols & Visualizations
General Experimental Workflow
The quantification of BiP follows a multi-step process from sample acquisition to final data analysis.
Caption: General workflow for BiP quantification.
Protocol 1: Sandwich ELISA for BiP Quantification
This protocol is adapted from commercially available human BiP/GRP78 ELISA kits.[12][20]
A. Materials:
-
BiP ELISA Kit (containing pre-coated 96-well plate, BiP standard, detection antibody, HRP conjugate, wash buffer, substrate, and stop solution)
-
Biological samples (serum, plasma, cell culture supernatant)
-
Microplate reader capable of reading absorbance at 450 nm
-
Precision pipettes and tips
-
Deionized water
B. Reagent Preparation:
-
Bring all reagents and samples to room temperature.
-
BiP Standard: Reconstitute the lyophilized BiP standard with the provided diluent to create a stock solution (e.g., 40 ng/mL).[20] Perform serial dilutions as per the kit manual to generate a standard curve (e.g., 40, 20, 10, 5, 2.5, 1.25, 0.63, 0 ng/mL).[20]
-
Wash Buffer: Dilute the concentrated wash buffer to 1X with deionized water.
C. Assay Procedure:
-
Add 100 µL of each standard, blank (0 ng/mL), and sample to the appropriate wells of the pre-coated microplate.
-
Cover the plate and incubate for 90 minutes at 37°C.[20]
-
Aspirate the liquid from each well. Wash each well 3 times with 300 µL of 1X Wash Buffer. Ensure complete removal of liquid after the final wash.
-
Add 100 µL of Biotinylated Detection Antibody to each well.
-
Cover the plate and incubate for 1 hour at 37°C.[20]
-
Aspirate and wash the wells 3 times as in step 3.
-
Add 100 µL of HRP Conjugate to each well.
-
Cover the plate and incubate for 30 minutes at 37°C.[20]
-
Aspirate and wash the wells 5 times as in step 3.
-
Add 90 µL of Substrate Reagent to each well. Incubate for 15 minutes at 37°C in the dark. A blue color will develop.
-
Add 50 µL of Stop Solution to each well. The color will change to yellow.
-
Read the absorbance of each well at 450 nm immediately.
D. Data Analysis:
-
Subtract the average absorbance of the blank from all other readings.
-
Plot the absorbance values for the standards against their known concentrations.
-
Generate a standard curve using a four-parameter logistic (4-PL) curve-fit.
-
Interpolate the concentration of BiP in the samples from the standard curve. Account for any sample dilution factors.
Protocol 2: Western Blot for Semi-Quantitative Analysis of BiP
This protocol is a general guide for detecting BiP in cell or tissue lysates.
A. Sample Preparation & Protein Quantification:
-
Lyse cells or homogenize tissue in RIPA buffer supplemented with protease inhibitors.
-
Centrifuge at ~14,000 x g for 15 minutes at 4°C to pellet cell debris.
-
Collect the supernatant (lysate) and determine the total protein concentration using a BCA or Bradford assay.
-
Prepare samples for loading by mixing 20-30 µg of total protein with Laemmli sample buffer and heating at 95-100°C for 5 minutes.
B. SDS-PAGE and Transfer:
-
Load prepared samples and a molecular weight marker onto a 4-12% SDS-PAGE gel.
-
Run the gel until adequate separation is achieved.
-
Transfer the separated proteins from the gel to a PVDF or nitrocellulose membrane.
-
(Optional) Stain the membrane with Ponceau S to verify transfer efficiency.
C. Immunodetection:
-
Blocking: Block the membrane in 5% non-fat dry milk or 5% BSA in Tris-Buffered Saline with 0.1% Tween-20 (TBST) for 1 hour at room temperature with gentle agitation.
-
Primary Antibody: Incubate the membrane with a primary antibody specific for BiP/GRP78 (e.g., rabbit anti-BiP, diluted 1:1000-1:5000 in blocking buffer) overnight at 4°C or for 1-2 hours at room temperature.[13][21]
-
Washing: Wash the membrane 3 times for 10 minutes each with TBST.
-
Secondary Antibody: Incubate the membrane with an HRP-conjugated secondary antibody (e.g., anti-rabbit IgG-HRP, diluted in blocking buffer) for 1 hour at room temperature.
-
Washing: Wash the membrane 3 times for 10 minutes each with TBST.
D. Detection and Analysis:
-
Incubate the membrane with an Enhanced Chemiluminescence (ECL) substrate according to the manufacturer's instructions.
-
Capture the chemiluminescent signal using a digital imager or X-ray film.
-
Perform densitometry analysis using imaging software. Quantify the band intensity for BiP (~78 kDa) and a loading control (e.g., β-actin, ~42 kDa).
-
Calculate the relative BiP expression by dividing the BiP band intensity by the corresponding loading control intensity for each sample.
Protocol 3: Mass Spectrometry for Absolute Quantification of BiP
This protocol outlines a targeted, bottom-up proteomics workflow.
A. Sample Preparation and Digestion:
-
Prepare protein lysates as described in the Western Blot protocol (Section 4.3.A).
-
Take a precise amount of total protein (e.g., 50 µg) from each sample.
-
Spike each sample with a known amount of a heavy-isotope labeled synthetic BiP peptide (e.g., containing ¹³C/¹⁵N-labeled Arginine or Lysine).
-
Reduction & Alkylation: Reduce disulfide bonds with DTT and alkylate cysteine residues with iodoacetamide.
-
Digestion: Digest the protein mixture into peptides using sequencing-grade trypsin overnight at 37°C.
-
Clean up the resulting peptide mixture using a C18 solid-phase extraction (SPE) column.
B. LC-MS/MS Analysis:
-
Inject the cleaned peptide sample into a high-performance liquid chromatography (HPLC) system coupled to a tandem mass spectrometer (e.g., a Q-Exactive or Triple Quadrupole instrument).
-
Separate peptides using a reverse-phase chromatography gradient.
-
Analyze the eluting peptides using a targeted MS method, such as Parallel Reaction Monitoring (PRM) or Multiple Reaction Monitoring (MRM). This involves programming the instrument to specifically isolate and fragment the precursor ions of both the endogenous (light) and standard (heavy) BiP peptides.
C. Data Analysis:
-
Process the raw MS data using specialized software (e.g., Skyline, MaxQuant).
-
Extract the ion chromatograms (XICs) for the specific fragment ions of the light and heavy BiP peptides.
-
Calculate the peak area ratio of the light (endogenous) to the heavy (standard) peptide.
-
Determine the absolute concentration of the BiP peptide in the original sample using the known concentration of the spiked-in heavy standard. Convert this to the concentration of the BiP protein based on its molecular weight.
BiP Signaling Pathway Visualization
BiP is a key regulator of the Unfolded Protein Response (UPR). Under ER stress, BiP dissociates from the stress sensors IRE1, PERK, and ATF6, leading to their activation and downstream signaling to restore proteostasis.[22][23]
Caption: BiP's role in the Unfolded Protein Response.
References
- 1. ER chaperone GRP78/BiP translocates to the nucleus under stress and acts as a transcriptional regulator - PMC [pmc.ncbi.nlm.nih.gov]
- 2. pnas.org [pnas.org]
- 3. Frontiers | Heat shock proteins in osteoarthritis: molecular mechanisms, pathogenic roles, and therapeutic opportunities [frontiersin.org]
- 4. captodayonline.com [captodayonline.com]
- 5. Characterization and Mechanism of Stress-induced Translocation of 78-Kilodalton Glucose-regulated Protein (GRP78) to the Cell Surface - PMC [pmc.ncbi.nlm.nih.gov]
- 6. Unfolded protein response - Wikipedia [en.wikipedia.org]
- 7. Endoplasmic reticulum chaperone GRP78/BiP is critical for mutant Kras-driven lung tumorigenesis - PMC [pmc.ncbi.nlm.nih.gov]
- 8. The Clinicopathological Significance of BiP/GRP-78 in Breast Cancer: A Meta-Analysis of Public Datasets and Immunohistochemical Detection - PMC [pmc.ncbi.nlm.nih.gov]
- 9. The Circulating GRP78/BiP Is a Marker of Metabolic Diseases and Atherosclerosis: Bringing Endoplasmic Reticulum Stress into the Clinical Scenario - PMC [pmc.ncbi.nlm.nih.gov]
- 10. Serum GRP78 as a Tumor Marker and Its Prognostic Significance in Non-Small Cell Lung Cancers: A Retrospective Study - PMC [pmc.ncbi.nlm.nih.gov]
- 11. mybiosource.com [mybiosource.com]
- 12. img.abclonal.com [img.abclonal.com]
- 13. GRP78/BIP antibody (11587-1-AP) | Proteintech [ptglab.com]
- 14. researchgate.net [researchgate.net]
- 15. tandfonline.com [tandfonline.com]
- 16. Protein Quantification in Clinical Research: Key Techniques - Creative Proteomics [creative-proteomics.com]
- 17. researchgate.net [researchgate.net]
- 18. Serum glucose-regulated protein 78 (GRP78) levels in COVID-19-associated mucormycosis: results of a case–control study - PMC [pmc.ncbi.nlm.nih.gov]
- 19. Expression and release of glucose-regulated protein-78 (GRP78) in multiple myeloma - PMC [pmc.ncbi.nlm.nih.gov]
- 20. Human BIP/GRP78 ELISA kit | Cell Culture Supernatant, Plasma, Serum [antibodies-online.com]
- 21. BiP Antibody | Cell Signaling Technology [cellsignal.com]
- 22. researchgate.net [researchgate.net]
- 23. researchgate.net [researchgate.net]
Troubleshooting & Optimization
Troubleshooting Bicep precipitation in solution
Bicep Precipitation Troubleshooting Center
This technical support center provides detailed troubleshooting guides and frequently asked questions (FAQs) to help researchers, scientists, and drug development professionals address issues with this compound precipitation in solution.
Frequently Asked Questions (FAQs)
???+ question "What are the most common causes of this compound precipitation?"
???+ question "My this compound solution became cloudy after purification. What should I check first?"
???+ question "How can stabilizing additives improve this compound solubility?"
Troubleshooting Guides & Experimental Protocols
Issue: this compound precipitates during buffer exchange or concentration.
This is often due to the final buffer conditions being suboptimal for this compound at a higher concentration. A systematic screening of buffer conditions is the most effective way to identify a formulation that maintains this compound solubility.
This protocol outlines a method to screen various buffer pH and salt concentrations to find optimal conditions for this compound stability.
Methodology:
-
Prepare this compound Stock: Start with a soluble, purified stock of this compound in its initial buffer at a known concentration (e.g., 1-2 mg/mL).
-
Prepare Buffer Matrix: Create a matrix of buffers in a 96-well plate. Vary the pH (e.g., from 5.0 to 8.5) and the ionic strength by altering the salt concentration (e.g., 50 mM, 150 mM, 300 mM NaCl). Commonly used buffers include citrate, histidine, and phosphate.[1]
-
Buffer Exchange: Exchange small aliquots of the this compound stock into each buffer condition using micro-dialysis cassettes or small size-exclusion chromatography columns.
-
Incubation & Monitoring: Incubate the plate under desired stress conditions (e.g., 4°C for 24 hours, or a thermal ramp from 25°C to 60°C).
-
Assess Precipitation: Monitor for precipitation visually. Quantify turbidity by measuring the absorbance at a high wavelength (e.g., 340 nm or 600 nm), where higher absorbance indicates more significant aggregation.
-
Identify Optimal Conditions: The conditions that result in the lowest turbidity are considered optimal for maintaining this compound solubility.
| Buffer Component | pH Range | Common Use |
| Sodium Citrate | 3.0 - 6.2 | Often used for proteins stable at acidic pH. |
| L-Histidine | 5.5 - 6.5 | Popular for antibody formulations.[1] |
| Sodium Phosphate | 6.0 - 7.5 | Widely used due to its physiological relevance.[2] |
| Tris-HCl | 7.0 - 9.0 | Common for proteins stable at neutral to alkaline pH. |
Issue: this compound is soluble initially but precipitates over time during storage.
This suggests a slow, time-dependent aggregation process, which can often be mitigated by the inclusion of stabilizing additives.
This protocol is designed to test the efficacy of different common additives in preventing the time-dependent precipitation of this compound.
Methodology:
-
Prepare Additive Stocks: Make concentrated stock solutions of various stabilizing agents (see table below).
-
Sample Preparation: In separate microcentrifuge tubes, add your this compound solution (in its optimal buffer as determined by Protocol 1).
-
Add Excipients: Spike each tube with a different additive to a desired final concentration. Include a control sample with no additive.
-
Incubation: Store the samples at the intended storage temperature (e.g., 4°C or -20°C).
-
Monitor Over Time: At regular intervals (e.g., 1, 3, 7, and 14 days), remove a small aliquot from each tube and measure for aggregation. This can be done by measuring turbidity (A340) or using Dynamic Light Scattering (DLS) to detect the formation of larger particles.
-
Select Best Additive: The additive that best minimizes the increase in turbidity or particle size over time is the most suitable stabilizer for long-term storage.
| Additive Class | Example | Typical Working Concentration | Primary Mechanism of Action |
| Osmolyte/Polyol | Glycerol | 5 - 20% (v/v) | Preferential exclusion, increases protein hydration.[3] |
| Sugar | Sucrose / Trehalose | 200 - 300 mM | Stabilizes against thermal stress, cryoprotectant.[4] |
| Amino Acid | L-Arginine | 50 - 500 mM | Suppresses aggregation by binding to surface patches.[3][] |
| Reducing Agent | DTT / TCEP | 1 - 5 mM | Prevents oxidation and intermolecular disulfide bonds.[3] |
| Detergent | Tween-20 | 0.01 - 0.1% (v/v) | Solubilizes hydrophobic regions.[3] |
References
Technical Support Center: Optimizing BiTE Concentration for Cell-Based Assays
This technical support center provides researchers, scientists, and drug development professionals with comprehensive troubleshooting guides and frequently asked questions (FAQs) to effectively optimize Bispecific T-cell Engager (BiTE) concentration for cell-based assays.
Frequently Asked Questions (FAQs)
Q1: What is a BiTE molecule and what is its mechanism of action?
A1: A Bispecific T-cell Engager (BiTE) is an artificial bispecific antibody designed to engage T-cells to recognize and eliminate cancer cells.[1][2] It consists of two single-chain variable fragments (scFvs): one binds to the CD3 receptor on the surface of T-cells, and the other binds to a tumor-associated antigen (TAA) on cancer cells.[1][3][4] This dual binding creates a synapse between the T-cell and the tumor cell, leading to T-cell activation and the release of cytotoxic granules containing perforin and granzymes, which induce apoptosis (programmed cell death) in the cancer cell.[1][3][5]
Q2: Why is optimizing the BiTE concentration crucial for my cell-based assay?
A2: Optimizing the BiTE concentration is critical to achieve a therapeutic window that maximizes tumor cell killing (efficacy) while minimizing off-target effects and excessive cytokine release (toxicity).[6] Supra-optimal concentrations can lead to T-cell over-activation and non-specific cytotoxicity, while sub-optimal concentrations will result in insufficient tumor cell lysis.[6]
Q3: What is the typical concentration range for BiTEs in in vitro assays?
A3: The optimal concentration of a BiTE molecule is highly dependent on the specific BiTE construct, the target and effector cells used, and the assay format. However, dose-response experiments often cover a broad range, from picomolar (pM) to nanomolar (nM) concentrations. For example, in some T-cell dependent cellular cytotoxicity (TDCC) assays, EC50 values (the concentration at which 50% of the maximum effect is observed) can be in the low pM range.[7] A typical starting concentration for a dose-response curve could be around 100 pM.[8]
Q4: What is the Effector-to-Target (E:T) ratio, and how does it relate to BiTE concentration?
A4: The Effector-to-Target (E:T) ratio is the ratio of effector cells (e.g., T-cells) to target cells (cancer cells) in a co-culture assay. This ratio is a critical parameter that influences the outcome of BiTE-mediated cytotoxicity assays. The optimal E:T ratio is system-dependent and should be empirically determined.[9] Commonly tested ratios include 1:1, 5:1, and 10:1.[9] The BiTE concentration required to achieve a certain level of cytotoxicity will vary depending on the E:T ratio used.
Q5: What are the key cell-based assays for characterizing BiTEs?
A5: The primary cell-based assays for BiTE characterization include:
-
Cytotoxicity Assays: To measure the ability of the BiTE to induce T-cell mediated killing of target cancer cells.[10][11]
-
T-cell Activation Assays: To confirm that the BiTE is activating T-cells, often by measuring the expression of activation markers like CD25 and CD69 via flow cytometry.[12]
-
Cytokine Release Assays: To quantify the release of cytokines (e.g., IFN-γ, TNF-α, IL-2) from activated T-cells, which is an indicator of both efficacy and potential for toxicity (Cytokine Release Syndrome).[13][14]
-
Binding Assays: To confirm the dual binding of the BiTE to both T-cells and target cells, often performed using flow cytometry.
Troubleshooting Guides
This section addresses common issues encountered during BiTE cell-based assays and provides potential solutions.
| Problem | Potential Cause | Troubleshooting Steps |
| High Background Signal / Non-specific Cell Lysis | 1. BiTE concentration is too high: Supra-optimal concentrations can cause antigen-independent T-cell activation.[6] 2. High Effector-to-Target (E:T) ratio: An excess of effector cells can lead to non-specific killing.[6] 3. Poor cell health: Unhealthy target or effector cells can lead to high spontaneous cell death. 4. Contamination: Mycoplasma or other microbial contamination can affect cell viability and assay performance. 5. Inadequate blocking: In fluorescence or luminescence-based assays, insufficient blocking can lead to high background.[15] | 1. Perform a dose-response curve to determine the optimal BiTE concentration with a clear therapeutic window. 2. Titrate the E:T ratio to find the lowest ratio that still provides a robust signal.[9] 3. Ensure cells are healthy and in the logarithmic growth phase before starting the experiment. 4. Regularly test cell cultures for mycoplasma contamination. 5. Optimize blocking buffer composition and incubation time. |
| Low or No Target Cell Lysis | 1. BiTE concentration is too low: Insufficient BiTE to bridge effector and target cells. 2. Low E:T ratio: Not enough effector cells to kill the target cells. 3. Low target antigen expression: Target cells may not express sufficient levels of the target antigen. 4. Inactive effector cells: T-cells may not be sufficiently activated or may be exhausted. 5. Incorrect assay setup or timing: The incubation time may be too short to observe significant cell lysis. | 1. Increase the BiTE concentration or test a broader range in your dose-response curve. 2. Increase the E:T ratio. 3. Verify target antigen expression on your target cell line using flow cytometry. 4. Check the viability and activation status of your effector cells. Consider using pre-activated T-cells if necessary. 5. Perform a time-course experiment to determine the optimal assay endpoint (e.g., 24, 48, 72 hours). |
| High Variability Between Replicates | 1. Inconsistent cell seeding: Uneven distribution of cells in the microplate wells. 2. Pipetting errors: Inaccurate dispensing of cells, BiTEs, or reagents. 3. Edge effects: Evaporation from the outer wells of the microplate can lead to variability. 4. Improper mixing: Inhomogeneous distribution of cells and reagents within the wells. | 1. Ensure cell suspensions are homogenous before and during plating. 2. Calibrate pipettes regularly and use proper pipetting techniques. 3. To minimize edge effects, do not use the outer wells of the plate for experimental samples; instead, fill them with sterile media or PBS. 4. Gently mix the plate after adding all components. |
| Poor Signal-to-Noise Ratio | 1. Suboptimal assay parameters: Incorrect BiTE concentration, E:T ratio, or incubation time. 2. Inappropriate assay readout: The chosen detection method may not be sensitive enough. 3. High autofluorescence: Cell culture media components (e.g., phenol red, serum) can cause high background in fluorescence-based assays.[16] | 1. Systematically optimize all assay parameters. 2. Consider using a more sensitive detection method (e.g., a luminescence-based cytotoxicity assay over a colorimetric one). A signal-to-noise ratio greater than 5 is desirable.[17] 3. Use phenol red-free media and consider reducing serum concentration during the assay. |
Experimental Protocols
Protocol 1: BiTE-mediated T-cell Dependent Cellular Cytotoxicity (TDCC) Assay
This protocol describes a luminescence-based assay to measure BiTE-mediated cytotoxicity.
Materials:
-
Target cells (expressing the tumor-associated antigen) engineered to express luciferase.
-
Effector cells (e.g., human peripheral blood mononuclear cells - PBMCs).
-
BiTE antibody.
-
Isotype control antibody.
-
Assay medium (e.g., RPMI + 10% FBS).
-
White, flat-bottom 96-well plates.
-
Luminescence-based cell viability reagent (e.g., CellTiter-Glo®).
-
Plate reader with luminescence detection capabilities.
Methodology:
-
Cell Preparation:
-
Harvest target and effector cells and ensure they are viable and in the logarithmic growth phase.
-
Wash the cells and resuspend them in assay medium at the desired concentrations.
-
-
Assay Setup (96-well plate):
-
Seed the target cells at a density of 1 x 10^4 cells/well in 50 µL of assay medium.
-
Prepare serial dilutions of the BiTE and isotype control antibodies at 4x the final desired concentrations.
-
Add 25 µL of the diluted antibodies to the respective wells.
-
Add 25 µL of the effector cell suspension to achieve the desired E:T ratio (e.g., for a 10:1 ratio, add 1 x 10^5 cells/well).
-
Include control wells:
-
Target cells only (for maximum signal).
-
Target cells + effector cells (no BiTE).
-
Medium only (for background).
-
-
-
Incubation:
-
Incubate the plate at 37°C in a 5% CO2 incubator for 48-72 hours.
-
-
Luminescence Measurement:
-
Equilibrate the plate and the luminescence reagent to room temperature.
-
Add the luminescence reagent to each well according to the manufacturer's instructions.
-
Mix the contents on an orbital shaker for 2 minutes to induce cell lysis.
-
Incubate at room temperature for 10 minutes to stabilize the luminescent signal.
-
Measure the luminescence using a plate reader.
-
-
Data Analysis:
-
Calculate the percentage of specific cytotoxicity for each BiTE concentration using the following formula: % Specific Lysis = (1 - (Signal_Experimental - Signal_Background) / (Signal_Max - Signal_Background)) * 100
-
Plot the % specific lysis against the BiTE concentration (log scale) and fit a dose-response curve to determine the EC50.
-
Protocol 2: Cytokine Release Assay (ELISA)
This protocol outlines the measurement of IFN-γ release from T-cells upon BiTE-mediated activation.
Materials:
-
Supernatants from the TDCC assay (from Protocol 1).
-
IFN-γ ELISA kit.
-
Plate reader with absorbance detection at 450 nm.
Methodology:
-
Sample Collection:
-
After the co-incubation period in the TDCC assay, centrifuge the 96-well plate at 300 x g for 5 minutes.
-
Carefully collect the supernatant from each well without disturbing the cell pellet.
-
Store the supernatants at -80°C until use.
-
-
ELISA Procedure:
-
Perform the IFN-γ ELISA according to the manufacturer's protocol.
-
Briefly, this involves coating a 96-well plate with a capture antibody, adding the collected supernatants and standards, followed by a detection antibody, an enzyme conjugate, and a substrate.
-
-
Data Analysis:
-
Measure the absorbance at 450 nm.
-
Generate a standard curve using the provided IFN-γ standards.
-
Determine the concentration of IFN-γ in each sample by interpolating from the standard curve.
-
Plot the IFN-γ concentration against the BiTE concentration to generate a dose-response curve.
-
Visualizations
References
- 1. researchgate.net [researchgate.net]
- 2. researchgate.net [researchgate.net]
- 3. researchgate.net [researchgate.net]
- 4. researchgate.net [researchgate.net]
- 5. researchgate.net [researchgate.net]
- 6. benchchem.com [benchchem.com]
- 7. researchgate.net [researchgate.net]
- 8. BiTE® T cell-dependent cellular cytotoxicity (TDCC) assay [protocols.io]
- 9. benchchem.com [benchchem.com]
- 10. Characterization of bispecific T-cell Engager (BiTE) antibodies with a high-capacity T-cell dependent cellular cytotoxicity (TDCC) assay - PubMed [pubmed.ncbi.nlm.nih.gov]
- 11. Cell-based assays to assess bispecific T cell engagers (BiTE) - Download new in vitro case study - Explicyte Immuno-Oncology [explicyte.com]
- 12. A simplified function-first method for the discovery and optimization of bispecific immune engaging antibodies - PMC [pmc.ncbi.nlm.nih.gov]
- 13. researchgate.net [researchgate.net]
- 14. Frontiers | Computational Analysis of Cytokine Release Following Bispecific T-Cell Engager Therapy: Applications of a Logic-Based Model [frontiersin.org]
- 15. azurebiosystems.com [azurebiosystems.com]
- 16. bitesizebio.com [bitesizebio.com]
- 17. nanotempertech.com [nanotempertech.com]
Technical Support Center: Enhancing Protein Stability for Long-Term Experiments
This technical support center provides researchers, scientists, and drug development professionals with comprehensive guidance on improving the stability of proteins, here referred to as "Bicep," for long-term experimental use. Below you will find troubleshooting guides, frequently asked questions (FAQs), and detailed experimental protocols to address common stability challenges.
Troubleshooting Guides
This section addresses specific issues that may arise during your experiments, with a question-and-answer format to guide you through potential solutions.
Issue: Protein Aggregation
Q1: What are the initial signs of this compound protein aggregation?
A1: Initial signs of this compound instability and aggregation can include the appearance of visible particulates or cloudiness in the solution (turbidity).[1] You might also observe a pellet after centrifugation.[1] Other indicators are a loss of biological activity and the presence of high molecular weight species in size-exclusion chromatography or dynamic light scattering analysis.[2][3]
Q2: My this compound protein is aggregating upon concentration. What can I do?
A2: Aggregation during concentration is a common issue.[4] Consider the following troubleshooting steps:
-
Reduce Protein Concentration: Higher concentrations increase the risk of aggregation.[2][5] If possible, work with a lower concentration or increase the sample volume during purification steps.[2]
-
Optimize Buffer Conditions: The pH and ionic strength of your buffer are critical.[5][6] Experiment with different pH values, typically +/- 1 unit from your protein's isoelectric point (pI), and screen various salt concentrations.[2][7]
-
Add Stabilizing Excipients: The addition of certain molecules can enhance stability. Consider including:
-
Glycerol or Ethylene Glycol: These cryoprotectants can prevent aggregation, especially during freeze-thaw cycles.[8][9] A concentration of 10-50% is a good starting point.[4][9]
-
Amino Acids: Arginine and glutamate can increase solubility by interacting with charged and hydrophobic regions on the protein surface.[2]
-
Detergents: Low concentrations of non-denaturing detergents (e.g., Tween 20, CHAPS) can help solubilize aggregates.[2][3]
-
-
Work at a Different Temperature: Performing purification and concentration steps at a lower temperature (e.g., 4°C) can sometimes reduce aggregation.[5]
Issue: Protein Degradation
Q3: I'm observing extra bands on my SDS-PAGE gel, suggesting this compound degradation. How can I prevent this?
A3: The appearance of extra, lower molecular weight bands is a classic sign of proteolytic degradation.[1][10] To mitigate this, consider these strategies:
-
Use Protease Inhibitor Cocktails: Add a commercially available protease inhibitor cocktail to your lysis and purification buffers immediately before use.[10]
-
Maintain a Cold Chain: Perform all purification steps at 4°C to minimize the activity of co-purifying proteases.[10][11]
-
Work Quickly: Minimize the time your protein spends in solution, especially during the initial purification stages when protease concentrations may be highest.[10]
-
Optimize pH: Proteases have optimal pH ranges for their activity. Working at a pH outside of this range can reduce their efficacy.[10]
Issue: Loss of Function
Q4: My this compound protein is losing its biological activity over time. What could be the cause?
A4: Loss of activity can be due to several factors, including aggregation, degradation, or improper folding.[12]
-
Confirm Structural Integrity: Use techniques like circular dichroism to check if the secondary structure of your protein is maintained.
-
Assess for Aggregation and Degradation: Follow the troubleshooting steps outlined above to rule out aggregation and degradation as the root cause.
-
Optimize Storage Conditions: Improper storage is a frequent cause of activity loss.[8] Ensure you are storing your protein at the optimal temperature and in a suitable buffer. For long-term storage, flash-freezing aliquots in liquid nitrogen and storing at -80°C is often recommended.[8][9][13] Avoid repeated freeze-thaw cycles.[8][14]
-
Add Stabilizing Additives: Besides cryoprotectants, consider adding:
-
Reducing Agents: For proteins with cysteine residues, including a reducing agent like DTT or TCEP (typically 1-5 mM) can prevent oxidation and maintain activity.[7][9]
-
Metal Chelators: If your protein is sensitive to metal-induced oxidation, add EDTA (1-5 mM) to your buffer.[13]
-
BSA as a Carrier Protein: For dilute protein solutions (<1 mg/mL), adding a carrier protein like Bovine Serum Albumin (BSA) can prevent loss of protein due to binding to storage tubes and can also have a stabilizing effect.[8][13]
-
Frequently Asked Questions (FAQs)
Q1: What is the best way to store my this compound protein for long-term experiments?
A1: For long-term storage (months to years), it is generally best to store the protein in single-use aliquots at -80°C or in liquid nitrogen.[8][9][13] The addition of a cryoprotectant like 50% glycerol can prevent damage from freezing.[8][14] Avoid repeated freeze-thaw cycles as they can lead to protein denaturation and aggregation.[8][14] For short-term storage (days to weeks), 4°C is often sufficient, but the risk of microbial growth and proteolytic degradation increases.[8][13]
Q2: How do I choose the right buffer for my this compound protein?
A2: The optimal buffer will depend on the specific properties of your protein.[6] Key factors to consider are:
-
pH: The buffer's pKa should be within one pH unit of your desired pH.[7] A common starting point is a pH of 7.4 to mimic physiological conditions, but the optimal pH for stability may be different.[7] Screening a range of pH values is recommended.[15]
-
Buffering Agent: Common buffers include Tris, PBS, histidine, and citrate.[6] Ensure the buffer itself does not interfere with your protein's activity or downstream applications.
-
Salt Concentration: The ionic strength of the buffer, controlled by the salt concentration, affects protein solubility and stability.[2] It's often necessary to empirically determine the optimal salt concentration.
Q3: What are some common additives to include in my protein buffer for enhanced stability?
A3: Several additives can be included to improve protein stability:[9][13]
-
Cryoprotectants: Glycerol or ethylene glycol (25-50%) for storage at -20°C or below.[9]
-
Reducing Agents: DTT or TCEP (1-5 mM) to prevent oxidation of cysteine residues.[7][9]
-
Metal Chelators: EDTA (1-5 mM) to prevent metal-induced oxidation.[13]
-
Antimicrobial Agents: Sodium azide (0.02-0.05%) or thimerosal (0.01%) to inhibit microbial growth during storage at 4°C.[9][13]
-
Inert Proteins: BSA (0.1-0.5%) to stabilize dilute protein solutions.[13]
Quantitative Data Summary
The following tables summarize key parameters for optimizing this compound stability based on common experimental observations.
Table 1: Recommended Buffer Conditions for this compound Stability
| Parameter | Recommended Range | Rationale |
| pH | pI ± 1 unit | Minimizes charge-charge repulsion or attraction that can lead to aggregation.[2][7] |
| Salt Concentration | 50-200 mM | Modulates electrostatic interactions to improve solubility.[2] |
| Buffer Concentration | 20-100 mM | Ensures sufficient buffering capacity.[7] |
Table 2: Common Additives for Enhancing this compound Stability
| Additive | Typical Concentration | Purpose |
| Glycerol | 10-50% (v/v) | Cryoprotectant, prevents aggregation.[8][9] |
| DTT/TCEP | 1-5 mM | Reducing agent, prevents cysteine oxidation.[7][9] |
| EDTA | 1-5 mM | Metal chelator, prevents oxidation.[13] |
| BSA | 0.1-1 mg/mL | Carrier protein, stabilizes dilute solutions.[13] |
| Sodium Azide | 0.02-0.05% (w/v) | Antimicrobial agent for 4°C storage.[13] |
Experimental Protocols
Protocol 1: Differential Scanning Fluorimetry (DSF) for Buffer Optimization
DSF is a rapid and high-throughput method to assess protein thermal stability by monitoring the fluorescence of a dye that binds to hydrophobic regions of a protein as it unfolds with increasing temperature. A higher melting temperature (Tm) indicates greater stability.
Methodology:
-
Prepare a master mix of your this compound protein (final concentration ~2 µM) and a fluorescent dye (e.g., SYPRO Orange).
-
In a 96-well or 384-well qPCR plate, dispense a range of different buffer conditions to be tested (varying pH, salt, and additives).
-
Add the protein/dye master mix to each well.
-
Seal the plate and briefly centrifuge.
-
Place the plate in a qPCR instrument and run a melt curve experiment, typically ramping the temperature from 25°C to 95°C.[1]
-
Analyze the data by plotting fluorescence versus temperature. The midpoint of the unfolding transition is the Tm.
-
Conditions that result in a higher Tm are considered more stabilizing for your this compound protein.[1]
Protocol 2: Dynamic Light Scattering (DLS) for Aggregate Detection
DLS is a non-invasive technique that measures the size distribution of particles in a solution, making it ideal for detecting the formation of protein aggregates over time.
Methodology:
-
Prepare samples of your this compound protein in the different buffer conditions you wish to evaluate.
-
Filter the samples through a 0.22 µm filter to remove any pre-existing large aggregates.[1]
-
Measure the initial particle size distribution using a DLS instrument.
-
Incubate the samples under the desired experimental conditions (e.g., prolonged storage at 4°C, elevated temperature).
-
Periodically take DLS measurements to monitor for changes in the particle size distribution.
-
An increase in the average particle size or the appearance of a new population of larger particles is indicative of aggregation.[1]
Visualizations
Caption: A flowchart for troubleshooting common this compound protein stability issues.
Caption: Workflow for systematically optimizing this compound protein stability.
References
- 1. benchchem.com [benchchem.com]
- 2. info.gbiosciences.com [info.gbiosciences.com]
- 3. biozentrum.unibas.ch [biozentrum.unibas.ch]
- 4. reddit.com [reddit.com]
- 5. benchchem.com [benchchem.com]
- 6. 5-considerations-for-buffer-optimization-during-biologics-pre-formulation [resources.nanotempertech.com]
- 7. bitesizebio.com [bitesizebio.com]
- 8. documents.thermofisher.com [documents.thermofisher.com]
- 9. bitesizebio.com [bitesizebio.com]
- 10. researchgate.net [researchgate.net]
- 11. youtube.com [youtube.com]
- 12. Surmodics - Guide to Determining Protein Stability in an Assay [shop.surmodics.com]
- 13. biocompare.com [biocompare.com]
- 14. neb.com [neb.com]
- 15. leukocare.com [leukocare.com]
Technical Support Center: Overcoming BiTE Resistance in Cell Lines
This technical support center provides researchers, scientists, and drug development professionals with comprehensive troubleshooting guides and frequently asked questions (FAQs) to address challenges encountered during in vitro experiments with Bispecific T-cell Engagers (BiTEs).
Frequently Asked Questions (FAQs)
Q1: What is the fundamental mechanism of action for BiTE antibodies in vitro?
A1: Bispecific T-cell Engagers (BiTEs) are artificial antibodies designed to physically link a T-cell to a cancer cell.[1][2] One arm of the BiTE molecule binds to the CD3 receptor on the surface of a T-cell, a key component of the T-cell receptor complex. The other arm binds to a specific tumor-associated antigen (TAA) on the surface of a cancer cell.[1][2] This cross-linking forces an immunological synapse to form between the T-cell and the tumor cell, leading to T-cell activation independent of major histocompatibility complex (MHC) presentation.[3] Activated T-cells then release cytotoxic granules containing perforin and granzymes, which induce apoptosis (programmed cell death) in the target cancer cell.[4]
Q2: What are the primary categories of BiTE resistance observed in cell line models?
A2: BiTE resistance in cell lines can be broadly categorized into two main types:
-
Tumor-Intrinsic Resistance: This originates from changes within the cancer cells themselves. Common mechanisms include the loss or downregulation of the target antigen, rendering the cancer cell "invisible" to the BiTE.[5] Other intrinsic factors involve alterations in signaling pathways that regulate apoptosis, making the cancer cells less susceptible to T-cell-mediated killing.[1][6]
-
Tumor-Extrinsic Resistance: This involves factors related to the effector T-cells or the in vitro tumor microenvironment. A primary mechanism is T-cell exhaustion, which can occur after prolonged stimulation and is characterized by the upregulation of inhibitory receptors like PD-1.[7][8][9] Additionally, the expression of co-stimulatory molecules on cancer cells, such as CD58, can influence the potency of BiTE-mediated T-cell activation.[1][5][6]
Q3: How can I establish a BiTE-resistant cell line for my experiments?
A3: Developing a BiTE-resistant cell line in vitro typically involves continuous or escalating exposure of a sensitive cancer cell line to a BiTE in the presence of effector T-cells. The general steps are as follows:
-
Determine the initial IC50: First, establish the half-maximal inhibitory concentration (IC50) of the BiTE for the parental cancer cell line in a standard cytotoxicity assay.
-
Continuous or Pulsed Exposure: Culture the parental cells with T-cells and the BiTE at a concentration around the IC10-IC20. This can be done continuously or in a pulsed manner, where the BiTE is added for a period and then removed to allow for recovery and selection of resistant clones.[10][11]
-
Dose Escalation: As the cells begin to proliferate in the presence of the BiTE, gradually increase the concentration of the BiTE in subsequent passages.[10][12]
-
Characterization: Once a cell population is established that can proliferate at a significantly higher BiTE concentration, characterize the resistance. This includes determining the new, higher IC50 and investigating the underlying mechanisms of resistance (e.g., target antigen expression, apoptosis pathway alterations).[10][11] It is crucial to cryopreserve cells at various stages of resistance development.
Troubleshooting Guides
Problem 1: Low or No Cytotoxicity Observed
| Potential Cause | Troubleshooting Steps |
| Suboptimal BiTE Concentration | Perform a dose-response curve with a broad range of BiTE concentrations (e.g., 0.1 pM to 100 nM) to determine the optimal effective concentration (EC50).[6] |
| Suboptimal Effector-to-Target (E:T) Ratio | Test a range of E:T ratios (e.g., 1:1, 5:1, 10:1, 20:1) to find the optimal ratio for your specific cell lines. Higher E:T ratios may be needed for less responsive target cells.[4][6] |
| Low Target Antigen Expression | Confirm the expression level of the target antigen on your cancer cell line using flow cytometry. If expression is low or heterogeneous, consider using a different cell line or a method to upregulate antigen expression if known. |
| Inactive or Exhausted T-cells | Ensure T-cells are healthy and functional. If using cryopreserved PBMCs, allow for a recovery period after thawing. For prolonged co-culture experiments, be aware of potential T-cell exhaustion, which can be assessed by monitoring inhibitory markers like PD-1 and LAG-3.[7][8] |
| Incorrect Assay Endpoint | The kinetics of BiTE-mediated killing can vary. Perform a time-course experiment (e.g., 24h, 48h, 72h) to determine the optimal incubation time for your specific assay and cell lines.[6] |
Problem 2: High Background or Non-Specific Cell Death
| Potential Cause | Troubleshooting Steps |
| High Effector-to-Target (E:T) Ratio | An excessive number of T-cells can lead to non-specific killing and high background lysis. Optimize the E:T ratio to the lowest level that provides specific killing of target cells.[6] |
| High BiTE Concentration | Supra-optimal concentrations of the BiTE can lead to over-activation of T-cells and non-specific cytotoxicity. Ensure you are working within the optimal range of your dose-response curve.[6] |
| Unhealthy Cells | Poor health of either the target or effector cells prior to the assay can result in high background cell death. Ensure cells are in the logarithmic growth phase and have high viability before starting the experiment. |
| Contamination | Microbial contamination (e.g., bacteria, yeast, mycoplasma) can cause cell death. Regularly check your cell cultures for contamination.[13][14] |
| "Bystander" Killing | Activated T-cells release pro-inflammatory cytokines (e.g., IFN-γ, TNF-α) that can induce apoptosis in nearby antigen-negative cells. To minimize this, use the lowest effective E:T ratio and consider the duration of the assay.[6] |
Signaling Pathways in BiTE Resistance
Intrinsic Resistance: Apoptosis Pathway Modulation
Cancer cells can develop resistance to BiTE-mediated killing by altering the extrinsic apoptosis pathway. Upregulation of anti-apoptotic proteins like Bcl-2 and c-FLIP can inhibit the caspase cascade, thereby preventing cell death even when T-cells are engaged.[1][6]
Caption: Intrinsic resistance via apoptosis pathway modulation.
Extrinsic Resistance: T-Cell Exhaustion
Prolonged exposure to tumor antigens via BiTEs can lead to T-cell exhaustion. This is characterized by the upregulation of inhibitory receptors like PD-1 on the T-cell surface. When PD-1 binds to its ligand, PD-L1, on the tumor cell, it triggers a signaling cascade that dampens T-cell activation and cytotoxic function.[7][8][9]
Caption: Extrinsic resistance via T-cell exhaustion pathway.
Experimental Protocols
Protocol 1: In Vitro BiTE-mediated Cytotoxicity Assay (LDH Release)
This protocol outlines a lactate dehydrogenase (LDH) release assay, a common method to measure cytotoxicity. LDH is a cytosolic enzyme released into the culture medium upon cell lysis.
Materials:
-
Target cancer cells
-
Effector cells (e.g., human PBMCs)
-
BiTE antibody and isotype control
-
Complete culture medium
-
96-well flat-bottom tissue culture plates
-
LDH cytotoxicity assay kit
Procedure:
-
Cell Preparation:
-
Harvest target cells during their logarithmic growth phase. Wash and resuspend in complete medium to a concentration of 1 x 10^5 cells/mL.
-
Isolate effector cells (e.g., PBMCs) and resuspend in complete medium to the desired concentration to achieve the target E:T ratio.
-
-
Assay Setup (in a 96-well plate):
-
Target Cell Seeding: Add 100 µL of the target cell suspension (10,000 cells) to each well. Incubate for 4-6 hours to allow adherent cells to attach.
-
Controls:
-
Spontaneous LDH Release (Target Cells): Wells with target cells and 100 µL of medium.
-
Spontaneous LDH Release (Effector Cells): Wells with effector cells and 100 µL of medium.
-
Maximum LDH Release (Target Cells): Wells with target cells. Add lysis buffer from the kit 45 minutes before the end of incubation.
-
Medium Background: Wells with 200 µL of medium only.
-
-
BiTE Dilutions: Prepare serial dilutions of your BiTE antibody and isotype control at 2x the final desired concentration.
-
Co-culture: Add 50 µL of the effector cell suspension and 50 µL of the 2x BiTE/control antibody solution to the appropriate wells. The final volume in each well should be 200 µL.
-
-
Incubation: Incubate the plate at 37°C in a 5% CO2 incubator for the desired time (e.g., 24-72 hours).
-
LDH Measurement:
-
45 minutes before the end of the incubation, add lysis buffer to the "Maximum LDH Release" wells.
-
Centrifuge the plate at 250 x g for 4 minutes.
-
Carefully transfer 50 µL of the supernatant from each well to a new 96-well plate.
-
Add 50 µL of the LDH reaction mixture from the kit to each well.
-
Incubate at room temperature for 30 minutes, protected from light.
-
Add 50 µL of the stop solution from the kit.
-
Measure the absorbance at 490 nm using a plate reader.
-
-
Data Analysis:
-
Subtract the absorbance of the medium background from all other readings.
-
Calculate the percentage of specific lysis using the following formula: % Specific Lysis = 100 x (Experimental Release - Spontaneous Release) / (Maximum Release - Spontaneous Release)
-
Caption: General workflow for an LDH release cytotoxicity assay.
Protocol 2: Flow Cytometry Analysis of Target Antigen Expression
This protocol is for quantifying the expression of the TAA on the surface of cancer cells.
Materials:
-
Parental and BiTE-resistant cancer cell lines
-
Phosphate-buffered saline (PBS)
-
FACS buffer (PBS + 2% FBS)
-
Fluorochrome-conjugated primary antibody against the TAA
-
Isotype control antibody
-
Flow cytometer
Procedure:
-
Cell Preparation: Harvest approximately 0.5-1 x 10^6 cells per sample. Wash the cells once with cold PBS.
-
Staining:
-
Resuspend the cell pellet in 100 µL of FACS buffer.
-
Add the primary antibody or the isotype control at the manufacturer's recommended concentration.
-
Incubate for 30 minutes at 4°C in the dark.
-
-
Washing: Wash the cells twice with 1 mL of cold FACS buffer, centrifuging at 300 x g for 5 minutes between washes.
-
Acquisition: Resuspend the final cell pellet in 300-500 µL of FACS buffer and acquire the samples on a flow cytometer.
-
Data Analysis:
-
Gate on the live cell population based on forward and side scatter.
-
Compare the median fluorescence intensity (MFI) of the TAA-stained cells to the isotype control to confirm specific staining.
-
Compare the MFI and percentage of positive cells between the parental and resistant cell lines.
-
Quantitative Data Summary
The following tables provide examples of how to structure quantitative data from BiTE cytotoxicity experiments.
Table 1: Effect of BiTE Concentration on Target Cell Lysis
| BiTE Concentration (ng/mL) | % Specific Lysis (24h) | % Specific Lysis (48h) |
| 0 (Control) | 5% | 8% |
| 0.1 | 25% | 45% |
| 1 | 50% | 75% |
| 10 | 85% | 95% |
| 100 | 88% | 96% |
Table 2: Impact of E:T Ratio on Target Cell Lysis
| E:T Ratio | % Specific Lysis (at optimal BiTE concentration) |
| 1:1 | 30% |
| 5:1 | 65% |
| 10:1 | 85% |
| 20:1 | 87% |
Table 3: Characterization of a BiTE-Resistant Cell Line
| Cell Line | BiTE IC50 (ng/mL) | Target Antigen MFI | % PD-L1 Positive Cells |
| Parental | 1.5 | 50,000 | 15% |
| Resistant | 150 | 5,000 | 60% |
References
- 1. jitc.bmj.com [jitc.bmj.com]
- 2. Bispecific T-Cell Engagers (BiTEs) | Moffitt [moffitt.org]
- 3. STAT3 Role in T-Cell Memory Formation - PMC [pmc.ncbi.nlm.nih.gov]
- 4. Apoptosis and its pathways as targets for intracellular pathogens to persist in cells - PMC [pmc.ncbi.nlm.nih.gov]
- 5. Frontiers | Mechanistic insights into resistance mechanisms to T cell engagers [frontiersin.org]
- 6. researchgate.net [researchgate.net]
- 7. ashpublications.org [ashpublications.org]
- 8. Functional exhaustion of CD4+ T cells induced by co‐stimulatory signals from myeloid leukaemia cells - PMC [pmc.ncbi.nlm.nih.gov]
- 9. Unravelling T cell exhaustion through co‐inhibitory receptors and its transformative role in cancer immunotherapy - PMC [pmc.ncbi.nlm.nih.gov]
- 10. researchgate.net [researchgate.net]
- 11. Bi-specific T-cell engagers (BiTEs) in prostate cancer and strategies to enhance development: hope for a BiTE-r future - PMC [pmc.ncbi.nlm.nih.gov]
- 12. STAT3: A Target to Enhance Antitumor Immune Response - PMC [pmc.ncbi.nlm.nih.gov]
- 13. Oncolytic herpesvirus expressing PD-L1 BiTE for cancer therapy: exploiting tumor immune suppression as an opportunity for targeted immunotherapy - PMC [pmc.ncbi.nlm.nih.gov]
- 14. Focal adhesion kinase signaling – tumor vulnerabilities and clinical opportunities - PMC [pmc.ncbi.nlm.nih.gov]
Azure Bicep Off-Target Effects: A Technical Support Center
This technical support center provides troubleshooting guides and frequently asked questions (FAQs) to help researchers, scientists, and drug development professionals mitigate off-target effects during their Azure Bicep deployments. In the context of Infrastructure as Code (IaC), "off-target effects" refer to unintended or unexpected consequences of deploying or modifying your Azure resources using this compound. These can range from deployment failures to the creation of misconfigured or insecure resources.
Frequently Asked Questions (FAQs)
Q1: What are the most common causes of this compound deployment failures?
A1: this compound deployments can fail for a variety of reasons, often stemming from issues within the this compound code or the Azure environment itself. The most common causes include:
-
Syntax Errors: Simple mistakes in the this compound syntax, such as a missing comma or incorrect function usage, can prevent a deployment from starting.[1]
-
Resource Dependencies: If the dependencies between resources are not correctly defined, Azure may attempt to create a resource before its required dependency is available, leading to a failure.[1]
-
Parameter Mismatches: Errors can occur if the parameters defined in your this compound file do not match the values provided during deployment in terms of name, type, or value.[1]
-
Insufficient Permissions: The identity performing the deployment may lack the necessary permissions to create, modify, or delete resources in the specified scope.[1]
-
Azure Resource Limits: Deployments can fail if they attempt to create resources that would exceed your Azure subscription's quotas for a particular resource type (e.g., number of VMs, storage accounts).[1]
-
API Version Incompatibility: Using an outdated API version for a resource in your this compound file can lead to failures, as the specified properties may no longer be supported.[1][2]
-
Resource Conflicts: Attempting to create a resource with a name that already exists in a conflicting state or is locked can cause a deployment error.[1]
Q2: How can I preview the changes my this compound file will make before deploying?
A2: To prevent unintended changes, you can use the "what-if" operation. This command analyzes your this compound file and the current state of your Azure environment to provide a detailed report of the resources that will be created, modified, or deleted. The what-if operation does not make any actual changes to your resources.[3] You can run this operation using Azure CLI or Azure PowerShell.[3]
Q3: What is "idempotency" in this compound and why does it sometimes seem to fail?
A3: Idempotency is the principle that deploying the same this compound file multiple times should result in the same resource state, without causing errors on subsequent runs. This compound itself is declarative and aims for idempotency. However, issues with idempotency are often not with this compound itself, but with how the underlying Azure resource providers handle updates.[4] For example, some resources may not allow certain properties to be modified after creation, leading to a failed deployment on the second run. In other cases, a resource provider might have a bug that causes non-idempotent behavior.[4][5]
Q4: How can I manage sensitive information like passwords and keys in my this compound files?
A4: To avoid exposing secrets in your source code, you should never hardcode them in your this compound files.[6] Instead, use the @secure() decorator for string or object parameters that contain sensitive data. This ensures that the values are not logged or stored in the deployment history.[6] For passing these secure values during deployment, you can use a separate parameters file (and add it to your .gitignore) or pass them directly via the command line.[6]
Troubleshooting Guides
Issue: Deployment Fails with "Resource Not Found" Error
This error typically occurs when your this compound template references a resource that does not exist or that it cannot access.
Troubleshooting Steps:
-
Verify Resource Existence: Ensure that the resource you are referencing (e.g., a virtual network, storage account) already exists in the specified resource group and subscription.
-
Check for Typos: Double-check the symbolic name and any resource IDs used in your this compound file for typographical errors.
-
Dependency Management: If the resource is being created in the same this compound file, ensure you are using implicit dependencies by referencing the resource's symbolic name. Avoid using the reference() and resourceId() functions when possible, as symbolic names create a more robust dependency chain.[7]
-
Cross-Scope Deployment: If the resource exists in a different resource group or subscription, ensure you are using the existing keyword with the correct scope to reference it.
Issue: Deployment Fails Due to a "Conflict"
A conflict error usually indicates that you are trying to perform an operation on a resource that is in a state that does not allow that operation.
Troubleshooting Steps:
-
Concurrent Deployments: Check if there are other deployments targeting the same resource group that are currently in progress. Wait for the concurrent deployment to complete before retrying.[8]
-
Resource State: Some operations are only allowed when a resource is in a specific state. For example, resizing a virtual machine disk may only be possible when the VM is deallocated.[8]
-
Idempotency Issues: As mentioned in the FAQ, some resources may not handle updates gracefully. If you are redeploying a template with changes, you may need to manually delete and recreate the resource.
Mitigating Off-Target Effects: Best Practice Protocols
To minimize the risk of unintended consequences, follow these best practice protocols when developing and deploying your this compound files.
Protocol 1: Pre-Deployment Validation and Testing
Objective: To catch errors and unintended changes before they are applied to your Azure environment.
Methodology:
-
Linting: Use the this compound linter to check your code for syntax errors and violations of best practices. The linter is integrated into the this compound extension for Visual Studio Code and can also be run from the command line.[9][10]
-
Validation: Before executing a deployment, use the az deployment group validate (Azure CLI) or Test-AzResourceGroupDeployment (Azure PowerShell) command to perform a preflight validation. This checks for errors that would block the deployment from starting.[11]
-
What-If Analysis: As a final pre-deployment step, run the what-if operation to get a detailed preview of the changes that will be made to your environment.[3]
Protocol 2: Secure Parameter Handling
Objective: To prevent the exposure of sensitive data in your this compound deployments.
Methodology:
-
Identify Sensitive Parameters: Review your this compound file and identify all parameters that will handle sensitive information, such as passwords, API keys, and connection strings.
-
Apply the @secure() Decorator: For each sensitive parameter, add the @secure() decorator on the line above the parameter declaration.
-
Externalize Secret Values: Do not provide default values for secure parameters in your this compound file. Instead, pass the values at deployment time using one of the following methods:
-
A separate .json parameters file that is excluded from source control.
-
Directly through the command line.
-
By referencing a secret from an Azure Key Vault.
-
Quantitative Data Summary: Common this compound Linter Rules
| Rule Name | Description | Default Level |
| no-unused-params | Checks for parameters that are declared but not used in the this compound file. | Warning |
| no-unused-vars | Checks for variables that are declared but not used. | Warning |
| no-hardcoded-env-urls | Checks for hardcoded environment URLs and recommends using the environment() function instead. | Warning |
| secure-parameter-default | Checks for secure parameters that have a default value. | Error |
| no-loc-expr-outside-params | Recommends that the resourceGroup().location or deployment().location expressions are only used as default values for parameters. | Warning |
This table summarizes a selection of common this compound linter rules that can help prevent off-target effects by enforcing coding standards.
Visualizations
Diagram: this compound Pre-Deployment Workflow
This diagram illustrates the recommended workflow to follow before deploying a this compound file to mitigate off-target effects.
Caption: this compound Pre-Deployment Best Practice Workflow.
Diagram: this compound Implicit vs. Explicit Dependencies
This diagram illustrates the logical relationship between implicit and explicit dependencies in this compound.
Caption: Comparison of this compound Dependency Types.
References
- 1. sqlstad.nl [sqlstad.nl]
- 2. sqlstad.nl [sqlstad.nl]
- 3. This compound What-If: Preview Changes Before Deployment - Azure Resource Manager | Microsoft Learn [learn.microsoft.com]
- 4. Reddit - The heart of the internet [reddit.com]
- 5. idempotency of resource creation in microsoft azure creating a virtual network - Stack Overflow [stackoverflow.com]
- 6. 7 Azure this compound Security Mistakes To Avoid (and how to) [intercept.cloud]
- 7. Learn best practices when developing this compound files - Azure Resource Manager | Microsoft Learn [learn.microsoft.com]
- 8. Troubleshoot common Azure deployment errors - Azure Resource Manager | Microsoft Learn [learn.microsoft.com]
- 9. Overview of deployment troubleshooting for this compound files and ARM templates - Azure Resource Manager | Microsoft Learn [learn.microsoft.com]
- 10. rabobank.jobs [rabobank.jobs]
- 11. Overview of deployment troubleshooting for this compound files and ARM templates - Azure Resource Manager | Azure Docs [docs.azure.cn]
Technical Support Center: Refining Bicep Treatment Duration in Experimental Setups
This technical support center provides researchers, scientists, and drug development professionals with troubleshooting guides and frequently asked questions (FAQs) to address specific issues encountered when refining the treatment duration of bivalent chemical entities (referred to as "Bicep" for the purpose of this guide) in experimental setups.
Frequently Asked Questions (FAQs)
Q1: What is a typical starting point for this compound treatment duration in a new experiment?
A1: For initial experiments, it is advisable to test a broad range of time points. A common starting point is to perform a time-course experiment with treatment durations of 2, 4, 8, 16, and 24 hours to capture the kinetics of protein degradation.[1] Some studies suggest starting with shorter time points (e.g., 2, 4, 6 hours) and extending to longer durations (e.g., 12, 24, 48 hours) to identify the point of maximal degradation.[2]
Q2: How quickly can I expect to see degradation of the target protein?
A2: The onset of protein degradation is often rapid. Significant reduction in target protein levels can be observed within 1 to 2 hours of treatment in vitro. Maximal degradation (Dmax) is frequently achieved between 2 and 24 hours, depending on the specific this compound compound, its concentration, the target protein's half-life, and the cell line used.
Q3: What is the "hook effect" and how does it relate to treatment duration?
A3: The "hook effect" is a phenomenon where the efficacy of a bivalent degrader decreases at very high concentrations. This occurs because the this compound molecule forms separate binary complexes with the target protein and the E3 ligase, rather than the productive ternary complex required for degradation. While primarily a concentration-dependent effect, using excessively high concentrations for a prolonged duration can exacerbate this issue and lead to misleading results. It is crucial to perform a dose-response experiment to identify the optimal concentration range before settling on a treatment duration.
Q4: How long should I treat cells to observe downstream signaling effects?
A4: The necessary treatment duration to observe downstream effects depends on the specific pathway. Changes in the direct target's phosphorylation status can be rapid. However, effects on downstream signaling cascades and subsequent changes in gene expression or protein levels may require longer incubation times. For instance, degradation of the epigenetic reader BRD4 leads to a rapid decrease in MYC mRNA and protein levels, while the induction of apoptosis, a more downstream effect, may take 24 to 72 hours to become apparent.
Q5: Can prolonged this compound treatment lead to off-target effects?
A5: Yes, prolonged exposure to any bioactive compound, including this compound degraders, can potentially lead to off-target effects or cellular toxicity. It is essential to determine the shortest duration that achieves the desired level of target degradation and biological effect to minimize these risks. Shorter treatment times (e.g., under 6 hours) are often used in global proteomics studies to identify the direct targets of degradation. Off-target effects can also arise from the individual components of the this compound molecule (the target-binding ligand and the E3 ligase-binding ligand) independent of the degradation mechanism.
Troubleshooting Guides
Issue 1: No or minimal degradation of the target protein is observed.
| Possible Cause | Troubleshooting Steps |
| Inappropriate Treatment Duration | The selected time point may be too early or too late to observe maximal degradation. Perform a time-course experiment (e.g., 0, 2, 4, 8, 16, 24 hours) to identify the optimal degradation window. |
| Suboptimal this compound Concentration | The concentration may be too low for effective ternary complex formation or too high, leading to the "hook effect". Conduct a dose-response experiment with a wide range of concentrations (e.g., from picomolar to micromolar) to determine the DC50 (concentration for 50% degradation) and Dmax (maximal degradation). |
| Poor Cell Permeability | The this compound compound may not be efficiently entering the cells. Ensure proper solubilization of the compound (e.g., in DMSO) and consider alternative delivery methods if permeability is a known issue for the chemical scaffold. |
| Low E3 Ligase Expression | The cell line used may have low endogenous expression of the E3 ligase recruited by the this compound (e.g., CRBN or VHL). Verify the expression level of the relevant E3 ligase in your cell line using Western blot or qPCR. If expression is low, consider using a different cell line.[2] |
| Compound Instability | The this compound molecule may be unstable in the cell culture medium over the chosen treatment duration. Prepare fresh dilutions of the degrader for each experiment. |
Issue 2: Inconsistent degradation results between experiments.
| Possible Cause | Troubleshooting Steps |
| Variability in Cell Culture | Differences in cell density, passage number, or cell health can lead to variable responses. Maintain consistent cell culture practices, use cells within a defined passage number range, and ensure cells are in the logarithmic growth phase. |
| Reagent Preparation | Inconsistent preparation of this compound dilutions or lysis buffers can introduce variability. Prepare fresh dilutions of the this compound for each experiment from a validated stock solution. Ensure lysis buffers contain fresh protease and phosphatase inhibitors.[3] |
| Technical Variability in Western Blotting | Inconsistent protein loading, transfer efficiency, or antibody dilutions can lead to variable results. Use a reliable loading control (e.g., GAPDH, β-actin) and consider total protein staining (e.g., Ponceau S) to verify equal loading and transfer.[3] |
Issue 3: Target protein levels recover too quickly after this compound washout.
| Possible Cause | Troubleshooting Steps |
| Rapid Protein Re-synthesis | The target protein may have a high turnover rate, leading to rapid re-synthesis once the this compound is removed. Consider the kinetics of protein re-synthesis when designing experiments that require sustained target knockdown. A washout experiment followed by a time-course analysis of protein levels can characterize the recovery rate. |
| Incomplete Washout | Residual this compound compound may still be present at low levels, leading to incomplete recovery. Ensure a thorough washout procedure with multiple washes of fresh media. |
Data Presentation: Quantitative Effects of this compound Treatment
The following tables provide a summary of typical quantitative data for well-characterized bivalent degraders targeting BRD4 and BTK.
Table 1: Representative Degradation Kinetics of BRD4 Degraders
| Degrader | Cell Line | DC50 | Dmax | Optimal Treatment Duration | Reference |
| ARV-825 | Burkitt's Lymphoma | <1 nM | >95% | 18 hours | [4] |
| MZ1 | HeLa | ~100 nM | ~90% | 6-24 hours | [5] |
| dBET1 | AML | ~30 nM | >90% | 2-6 hours |
Table 2: Representative Degradation Kinetics of BTK Degraders
| Degrader | Cell Line | DC50 | Dmax | Optimal Treatment Duration | Reference |
| RC-1 | MOLM-14 | 8-40 nM | >90% | 16 hours | [6] |
| P13I | JeKo-1 | ~25 nM | >80% | 24 hours | [6] |
| NC-1 | CLL cells | <100 nM | >90% | 16 hours | [7] |
Experimental Protocols
Protocol 1: Time-Course Experiment for Determining Optimal this compound Treatment Duration
This protocol outlines the steps to determine the kinetics of target protein degradation following treatment with a this compound compound.
Materials:
-
Cells of interest
-
Complete cell culture medium
-
This compound compound stock solution (e.g., in DMSO)
-
Vehicle control (e.g., DMSO)
-
6-well or 12-well tissue culture plates
-
Ice-cold PBS
-
RIPA lysis buffer supplemented with protease and phosphatase inhibitors
-
BCA Protein Assay Kit
-
Laemmli sample buffer
-
Equipment for Western blotting
Procedure:
-
Cell Seeding: Seed cells at a density that will ensure they are in the logarithmic growth phase and do not exceed 90% confluency by the end of the experiment. Allow cells to adhere overnight.
-
This compound Treatment: Treat the cells with a fixed concentration of the this compound compound (a concentration known to be effective, e.g., 5-10 times the DC50, if known). Include a vehicle control (e.g., DMSO at a final concentration ≤ 0.1%).
-
Time-Course Collection: Harvest cells at various time points after treatment (e.g., 0, 2, 4, 8, 16, and 24 hours). The "0 hour" time point represents the untreated control.[1]
-
Cell Lysis:
-
Place the culture plates on ice.
-
Aspirate the medium and wash the cells twice with ice-cold PBS.
-
Add an appropriate volume of ice-cold RIPA buffer with inhibitors to each well.
-
Scrape the cells and transfer the lysate to a pre-chilled microcentrifuge tube.
-
Incubate on ice for 30 minutes, vortexing briefly every 10 minutes.
-
Centrifuge the lysates at 14,000 x g for 15 minutes at 4°C to pellet cell debris.
-
Transfer the supernatant (protein lysate) to a new, pre-chilled tube.
-
-
Protein Quantification: Determine the protein concentration of each lysate using a BCA assay according to the manufacturer's instructions.
-
Sample Preparation for Western Blot:
-
Normalize the protein concentration of all samples with lysis buffer.
-
Add Laemmli sample buffer to the lysates and boil at 95-100°C for 5-10 minutes to denature the proteins.
-
-
Western Blot Analysis:
-
Load equal amounts of protein (e.g., 20-30 µg) per lane on an SDS-PAGE gel.
-
Perform electrophoresis and transfer the proteins to a PVDF or nitrocellulose membrane.
-
Block the membrane and incubate with primary antibodies against the target protein and a loading control (e.g., GAPDH, β-actin).
-
Incubate with the appropriate HRP-conjugated secondary antibody.
-
Develop the blot using an ECL substrate and capture the chemiluminescent signal.
-
-
Data Analysis:
-
Quantify the band intensities for the target protein and the loading control.
-
Normalize the target protein signal to the loading control for each time point.
-
Calculate the percentage of remaining target protein at each time point relative to the 0-hour time point (set to 100%).
-
Plot the percentage of remaining protein versus time to visualize the degradation kinetics and determine the optimal treatment duration for maximal degradation.
-
Protocol 2: Cell Viability Assay (MTT Assay)
This protocol is used to assess the cytotoxicity of the this compound compound at different treatment durations.
Materials:
-
Cells of interest
-
Complete cell culture medium
-
This compound compound stock solution
-
96-well clear-bottom tissue culture plates
-
MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) solution (5 mg/mL in PBS)
-
Solubilization solution (e.g., DMSO or a solution of 10% SDS in 0.01 M HCl)
-
Microplate reader
Procedure:
-
Cell Seeding: Seed cells in a 96-well plate at a predetermined optimal density (e.g., 5,000-10,000 cells/well) in 100 µL of medium. Allow cells to adhere overnight.
-
Drug Treatment: Treat the cells with the desired concentrations of the this compound compound. Include a vehicle-only control.
-
Incubation: Incubate the plate for the desired treatment durations (e.g., 24, 48, 72 hours).
-
MTT Addition: At the end of each incubation period, add 10 µL of MTT solution to each well.
-
Incubation with MTT: Incubate the plate for 2-4 hours at 37°C, allowing viable cells to reduce the MTT to formazan crystals.
-
Solubilization: Add 100 µL of solubilization solution to each well and mix thoroughly to dissolve the formazan crystals.
-
Absorbance Measurement: Measure the absorbance at 570 nm using a microplate reader.
-
Data Analysis:
-
Subtract the background absorbance (from wells with medium only).
-
Calculate the percentage of cell viability for each treatment condition relative to the vehicle-treated control (set to 100%).
-
Plot the percentage of cell viability against the this compound concentration for each treatment duration.
-
Mandatory Visualizations
Signaling Pathways and Experimental Workflows
Mechanism of this compound-mediated protein degradation.
Experimental workflow for a time-course experiment.
Downstream signaling effects of BRD4 degradation.
Downstream signaling effects of BTK degradation.
References
- 1. researchgate.net [researchgate.net]
- 2. researchgate.net [researchgate.net]
- 3. creative-diagnostics.com [creative-diagnostics.com]
- 4. Degradation and inhibition of epigenetic regulatory protein BRD4 exacerbate Alzheimer’s disease-related neuropathology in cell models - PMC [pmc.ncbi.nlm.nih.gov]
- 5. benchchem.com [benchchem.com]
- 6. Targeting Protein Kinases Degradation by PROTACs - PMC [pmc.ncbi.nlm.nih.gov]
- 7. Proteolysis Targeting Chimeras for BTK Efficiently Inhibit B-Cell Receptor Signaling and Can Overcome Ibrutinib Resistance in CLL Cells - PMC [pmc.ncbi.nlm.nih.gov]
Technical Support Center: Bicep-X Solubility and Recommended Solvents
This guide provides researchers, scientists, and drug development professionals with essential information regarding the solubility of the hypothetical peptide therapeutic, Bicep-X. It includes frequently asked questions, troubleshooting advice, quantitative solubility data, and detailed experimental protocols.
Frequently Asked Questions (FAQs) & Troubleshooting
Q1: What is the best initial solvent to try for solubilizing this compound-X?
A1: For any new peptide, the recommended starting solvent is sterile, distilled water.[1] If this compound-X fails to dissolve in water, the next choice of solvent depends on the peptide's overall charge, which can be calculated based on its amino acid composition.[2][3]
-
For acidic peptides (net negative charge): Try a dilute basic solution like 0.1 M ammonium bicarbonate.[4]
-
For basic peptides (net positive charge): Use a dilute acidic solution, such as 10% acetic acid.[2][3]
-
For neutral or hydrophobic peptides: These may require a small amount of an organic solvent like Dimethyl Sulfoxide (DMSO) or Dimethylformamide (DMF) for initial dissolution, followed by slow dilution with your aqueous buffer.[4][5]
Q2: My this compound-X peptide won't dissolve, even after trying the recommended starting solvents. What are my next steps?
A2: If initial attempts fail, several techniques can help improve solubility:
-
Sonication: Brief periods of sonication in a water bath can help break up aggregates and facilitate dissolution.[3][4]
-
Gentle Warming: Warming the solution to a temperature below 40°C can increase solubility. However, this should be done with caution to avoid peptide degradation.[4][5]
-
pH Adjustment: The solubility of a peptide is often lowest at its isoelectric point (pI). Adjusting the pH of the solution to be at least one unit away from the pI can significantly improve solubility.[4][6]
-
Test a small amount first: Before dissolving the entire sample, it is best to test the solubility with a small portion.[1][2][5]
Q3: this compound-X dissolved in an organic solvent but precipitated when I added my aqueous buffer. How can I prevent this?
A3: This is a common issue when a peptide transitions from a favorable organic environment to a less favorable aqueous one. To mitigate this, add the organic stock solution dropwise into the vigorously stirring aqueous buffer.[4] This slow dilution helps to prevent localized high concentrations of the peptide that can lead to aggregation and precipitation.
Q4: Can I use DMSO to dissolve this compound-X for cell-based assays?
A4: DMSO is a common choice for dissolving hydrophobic peptides and is generally tolerated in cell culture at low concentrations.[5] However, it is crucial to keep the final concentration of DMSO in your assay below 1% (v/v) to avoid cytotoxicity.[7] If this compound-X contains cysteine or methionine residues, be aware that DMSO can oxidize these side chains.[7][8]
Q5: The this compound-X solution appears cloudy or has formed a gel. What does this indicate?
A5: A cloudy solution suggests that the peptide is suspended rather than fully dissolved. Gel formation can occur with peptides that are prone to forming intermolecular hydrogen bonds.[5] In both cases, a stronger solvent system or the use of chaotropic agents like 6M guanidine hydrochloride (for non-cellular assays) may be necessary to disrupt aggregation.[4]
Quantitative Solubility Data for this compound-X
The following table summarizes the approximate solubility of this compound-X in various solvents at 25°C. These values are intended as a guide; optimal conditions may vary.
| Solvent/Buffer System | Concentration (mg/mL) | Observations |
| Deionized Water | < 0.1 | Insoluble |
| Phosphate-Buffered Saline (PBS), pH 7.4 | < 0.1 | Insoluble |
| 10% (v/v) Acetic Acid in Water | > 10 | Forms a clear solution |
| 0.1 M Ammonium Bicarbonate, pH 8.0 | 0.5 | Forms a slightly hazy suspension |
| Dimethyl Sulfoxide (DMSO) | > 25 | Readily dissolves |
| Dimethylformamide (DMF) | > 25 | Readily dissolves |
| 50% Acetonitrile in Water | 1 | Soluble with sonication |
Detailed Experimental Protocols
Protocol for Determining Peptide Solubility
This protocol outlines a systematic approach to determine the solubility of this compound-X.
Materials:
-
Lyophilized this compound-X peptide
-
Sterile, deionized water
-
10% (v/v) acetic acid
-
0.1 M ammonium bicarbonate
-
DMSO
-
Vortex mixer
-
Centrifuge
-
Spectrophotometer or HPLC
Procedure:
-
Preparation: Allow the lyophilized this compound-X to warm to room temperature before opening the vial.
-
Initial Test in Water: Weigh out approximately 1 mg of this compound-X into a microcentrifuge tube. Add 100 µL of sterile, deionized water to achieve a target concentration of 10 mg/mL. Vortex the tube for 30 seconds.
-
Visual Inspection: Visually inspect the solution. If it is clear, the peptide is soluble at that concentration. If it is cloudy or contains visible particles, the peptide is not fully dissolved.
-
Systematic Solvent Testing: If the peptide is insoluble in water, proceed with testing other solvents on fresh 1 mg aliquots of the peptide. Test solvents in the following order, proceeding to the next only if the previous one fails:
-
10% Acetic Acid
-
0.1 M Ammonium Bicarbonate
-
DMSO
-
-
Quantification (Optional): To determine the exact solubility, centrifuge the suspension at 14,000 rpm for 10 minutes.[9] Carefully collect the supernatant and measure the peptide concentration using a spectrophotometer (at 280 nm, if the peptide contains Trp or Tyr) or by HPLC analysis. The concentration of the supernatant represents the solubility limit in that solvent.
-
Record Keeping: Document the solvent, the maximum concentration at which a clear solution is obtained, and any observations such as the need for vortexing, sonication, or warming.
Visualizations
Troubleshooting Workflow for this compound-X Solubility
The following diagram outlines a logical workflow for troubleshooting common solubility issues with this compound-X.
Caption: A workflow for troubleshooting this compound-X peptide solubility.
Hypothetical Signaling Pathway for this compound-X
This diagram illustrates a hypothetical signaling pathway where this compound-X acts as an antagonist to an orphan G-protein coupled receptor (GPCR).
Caption: Hypothetical signaling pathway for this compound-X as a GPCR antagonist.
References
- 1. genscript.com [genscript.com]
- 2. biobasic.com [biobasic.com]
- 3. Peptide Solubility Guidelines - How to solubilize a peptide [sb-peptide.com]
- 4. benchchem.com [benchchem.com]
- 5. wolfson.huji.ac.il [wolfson.huji.ac.il]
- 6. The Solubility Challenge in Peptide Therapeutics | Blog | Biosynth [biosynth.com]
- 7. jpt.com [jpt.com]
- 8. chemistry.stackexchange.com [chemistry.stackexchange.com]
- 9. Interpretation of the dissolution of insoluble peptide sequences based on the acid-base properties of the solvent - PMC [pmc.ncbi.nlm.nih.gov]
Technical Support Center: Preventing Protein Degradation During Sample Processing
This technical support center provides researchers, scientists, and drug development professionals with troubleshooting guides and frequently asked questions (FAQs) to mitigate protein degradation during sample processing.
Frequently Asked Questions (FAQs)
Q1: What are the primary causes of protein degradation during sample processing?
Protein degradation during sample processing is primarily caused by the activity of proteases, which are enzymes that break down proteins.[1][2][3] These proteases can be released from cellular compartments, such as lysosomes, during sample lysis.[4] Other contributing factors include:
-
Temperature: Elevated temperatures can increase protease activity and lead to protein denaturation.[5][6]
-
pH: Suboptimal pH can lead to protein instability and denaturation.[1][5] Proteases are often less active at basic pH.[2]
-
Mechanical Stress: Physical disruption methods like sonication or excessive agitation can cause protein denaturation and aggregation.[7]
-
Repeated Freeze-Thaw Cycles: Repeatedly freezing and thawing samples can lead to protein aggregation and degradation.[8][9]
-
Contaminants: The presence of contaminating agents or salts from purification buffers can lead to protein precipitation and denaturation.[7]
-
Oxidation: Exposure to oxygen and transition metals can lead to protein oxidation and subsequent decomposition.[6]
Q2: How can I minimize protease activity during my experiments?
Minimizing protease activity is crucial for preserving your protein of interest. Here are several effective strategies:
-
Work at Low Temperatures: Always keep your samples on ice or in a cold room (4°C) during processing to reduce enzymatic activity.[1][2][4]
-
Use Protease Inhibitor Cocktails: Add a commercially available protease inhibitor cocktail to your lysis buffer.[1][5][8] These cocktails contain a mixture of inhibitors that target different classes of proteases.
-
Maintain an Optimal pH: For many proteins, a slightly basic pH (around 9 or greater) can help reduce the activity of common proteases.[2]
-
Work Quickly: Minimize the time between sample collection and processing to limit the window for proteolytic degradation.[5]
Q3: What is the best way to store my protein samples to prevent degradation?
Proper storage is critical for long-term protein stability. The ideal storage method depends on the intended downstream application.
-
Snap-Freezing: For long-term storage, snap-freeze your protein aliquots in liquid nitrogen or on dry ice to prevent the formation of ice crystals that can damage proteins.[10]
-
Ultra-Low Temperature Storage: Store frozen aliquots at -80°C for long-term stability.[8][10] For indefinite storage, vapor-phase liquid nitrogen (around -150°C) is recommended.[10]
-
Avoid Repeated Freeze-Thaw Cycles: Aliquot your samples into smaller, single-use volumes to avoid repeated freezing and thawing, which can cause protein aggregation and degradation.[8]
-
Stabilizing Reagents: For short-term storage at 4°C or room temperature when freezing is not immediately possible, consider using stabilizing reagents like RNAlater for tissue samples.[10][11]
Troubleshooting Guide
Problem: I'm observing multiple bands or a smear on my Western blot, suggesting my protein is degraded.
This is a common issue that can often be resolved by optimizing your sample preparation protocol.
Possible Causes and Solutions:
| Possible Cause | Troubleshooting Steps |
| Protease Contamination | Add a fresh protease inhibitor cocktail to your lysis buffer immediately before use.[1][5][12] Consider using a broader spectrum cocktail. |
| Suboptimal Temperature | Ensure all steps of your sample processing are performed on ice or in a cold room (4°C).[1][2][4] |
| Incorrect pH | Check and adjust the pH of your lysis buffer. A basic pH (e.g., 9.0) can inactivate some proteases.[2] |
| Delayed Processing | Process samples as quickly as possible after collection.[5] |
| Inadequate Denaturation | Ensure complete denaturation by heating your samples in SDS-PAGE sample buffer at 95-100°C for 5-10 minutes immediately after addition of the buffer.[12][13] For membrane proteins that may aggregate upon heating, consider a milder denaturation at 37°C for 30-60 minutes.[7] |
| Repeated Freeze-Thaw Cycles | Prepare single-use aliquots of your samples to avoid multiple freeze-thaw cycles.[8] |
Experimental Protocols
Protocol 1: General Protein Extraction with Minimized Degradation
This protocol provides a basic framework for extracting proteins from cultured cells while minimizing degradation.
Materials:
-
Phosphate-buffered saline (PBS), ice-cold
-
Lysis Buffer (e.g., RIPA buffer) supplemented with a protease inhibitor cocktail (added fresh)
-
Cell scraper
-
Microcentrifuge tubes, pre-chilled
-
Refrigerated microcentrifuge (4°C)
Procedure:
-
Place the cell culture dish on ice and wash the cells with ice-cold PBS.
-
Aspirate the PBS and add ice-cold lysis buffer containing a freshly added protease inhibitor cocktail.
-
Scrape the cells from the dish and transfer the lysate to a pre-chilled microcentrifuge tube.
-
Incubate the lysate on ice for 30 minutes with gentle vortexing every 10 minutes.
-
Centrifuge the lysate at 13,000 rpm for 15 minutes at 4°C to pellet the cell debris.[9]
-
Carefully transfer the supernatant (containing the soluble proteins) to a new pre-chilled tube.
-
Determine the protein concentration using a standard protein assay.
-
Add SDS-PAGE sample buffer and immediately heat the samples at 95-100°C for 5-10 minutes.
-
Store the samples at -80°C in single-use aliquots.
Visual Guides
References
- 1. researchgate.net [researchgate.net]
- 2. youtube.com [youtube.com]
- 3. Proteases: Multifunctional Enzymes in Life and Disease - PMC [pmc.ncbi.nlm.nih.gov]
- 4. arrow.tudublin.ie [arrow.tudublin.ie]
- 5. researchgate.net [researchgate.net]
- 6. Instability Challenges and Stabilization Strategies of Pharmaceutical Proteins - PMC [pmc.ncbi.nlm.nih.gov]
- 7. researchgate.net [researchgate.net]
- 8. researchgate.net [researchgate.net]
- 9. researchgate.net [researchgate.net]
- 10. Long-Term Biological Sample Storage: Comprehensive Best Practices Guide — Veritas Innovation [veritasinnovation.com]
- 11. Assessment of different preservation techniques for human skeletal muscle biopsy samples: A comparative method study on freeze‐drying, RNAlater, and RNAlater‐ICE - PMC [pmc.ncbi.nlm.nih.gov]
- 12. researchgate.net [researchgate.net]
- 13. Common artifacts and mistakes made in electrophoresis - PMC [pmc.ncbi.nlm.nih.gov]
Technical Support Center: Optimizing BiP Efficacy in Different Buffer Systems
This technical support center is designed for researchers, scientists, and drug development professionals to provide guidance on optimizing experiments involving the Binding immunoglobulin Protein (BiP), also known as GRP78 or HSPA5. Here, you will find troubleshooting guides and frequently asked questions (FAQs) to address common issues encountered during in vitro assays of BiP efficacy.
Frequently Asked Questions (FAQs)
Q1: What is the optimal pH for BiP activity?
A1: The optimal pH for BiP's ATPase activity has been observed to be around 5.0 in some studies. However, to mimic physiological conditions of the endoplasmic reticulum, most in vitro assays are performed in a pH range of 7.0 to 8.0.[1] For instance, substrate binding assays are commonly conducted at pH 7.5, while ATPase activity is often measured at a pH of 7.8.[1][2] It is critical to use a reliable buffer to maintain a stable pH, as fluctuations can alter the charge of both BiP and its substrate, thereby affecting their interaction.
Q2: How does the choice of buffer system (e.g., HEPES vs. Tris vs. Phosphate) impact BiP efficacy?
A2: While many studies on BiP do not offer a direct comparative analysis of different buffer systems, the choice of buffer is crucial.
-
HEPES is frequently used for BiP assays due to its pKa of ~7.5, which provides stable buffering in the physiological pH range of 6.8-8.2.[1][3][4][5] It has minimal metal ion binding and is generally considered inert in many biological systems.[4]
-
Tris is another common buffer with an effective pH range of 7.0-9.2.[4][6] However, its pKa is more sensitive to temperature changes compared to HEPES.[4] Tris contains a primary amine that can potentially interact with other components in the assay.[4]
-
Phosphate buffer is widely used in biological research but can precipitate with divalent cations like Ca²⁺ and Mg²⁺, which are important for BiP's function.[4][6]
The optimal buffer is often protein-dependent, and it is recommended to screen different buffer systems if you encounter issues with BiP activity or stability.[3]
Q3: What is the effect of salt concentration (ionic strength) on BiP's function?
A3: Ionic strength is a critical parameter in BiP assays. Salt concentrations, typically using KCl or NaCl, between 50 mM and 150 mM are common.[1] The effect of salt can be substrate-dependent. For substrates where electrostatic interactions are important for binding to BiP, increasing the salt concentration can weaken the binding affinity due to charge screening.[1] For example, the binding of BiP to certain oligomerized client proteins is highly dependent on salt concentration.[1] In some ATPase assays, KCl has been shown to yield higher activity compared to NaCl at the same concentration.[7]
Q4: Why are nucleotides (ATP and ADP) essential in BiP assays?
A4: BiP's chaperone activity is tightly regulated by its ATP hydrolysis cycle.
-
ATP-bound state: BiP has a low affinity for its substrates, with fast binding and release rates.
-
ADP-bound state: After ATP hydrolysis, BiP transitions to a high-affinity state for its substrate, characterized by slow binding and release.[1] Therefore, for studying stable BiP-substrate binding, ADP should be included in the buffer. Conversely, to study substrate release, ATP is necessary.
Q5: What is the role of divalent cations like Mg²⁺ and Mn²⁺ in BiP assays?
A5: Divalent cations are essential cofactors for BiP's ATPase activity.[8] Both Mg²⁺ and Mn²⁺ can stimulate ATP hydrolysis, with optimal concentrations typically in the low micromolar to millimolar range.[2] Mg²⁺ is the most commonly used divalent cation in BiP assays. In contrast, Ca²⁺ does not support BiP's ATPase activity.[2]
Q6: Should I include detergents or reducing agents in my buffer?
A6:
-
Detergents: Low concentrations (e.g., 0.01% - 0.1%) of non-ionic detergents like Tween-20 or Triton X-100 can be beneficial to prevent non-specific binding of proteins to plates or other surfaces, and to reduce protein aggregation.[1]
-
Reducing Agents: If your experiment is sensitive to oxidation, including a reducing agent like DTT or TCEP can be important to maintain the integrity of cysteine residues in BiP and its substrates.
Data Presentation: Optimizing Buffer Conditions for BiP Assays
The following tables summarize key quantitative data on the influence of buffer components on BiP efficacy.
Table 1: Effect of pH on BiP ATPase Activity
| pH | Relative ATPase Activity (%) | Buffer System Used | Reference |
| 4.0 | ~40 | Various | [7] |
| 5.0 | 100 | Various | [7] |
| 6.0 | ~70 | Various | [7] |
| 7.0 | ~50 | Various | [7] |
| 8.0 | ~30 | Various | [7] |
| 9.0 | ~20 | Various | [7] |
Note: While the optimal pH for ATPase activity was found to be 5.0, most functional assays are conducted at a physiological pH of ~7.0-7.5 to better reflect the conditions of the endoplasmic reticulum.[7]
Table 2: Influence of Salt Type and Concentration on BiP ATPase Activity
| Salt | Concentration (mM) | Relative ATPase Activity (%) | Reference |
| KCl | 25 | 100 | [7] |
| NaCl | 25 | ~80 | [7] |
| KCl | 100 | ~75 | [7] |
| NaCl | 100 | ~60 | [7] |
| KCl | 200 | ~50 | [7] |
| NaCl | 200 | ~40 | [7] |
Table 3: Recommended Buffer Compositions for Different BiP Assays
| Assay Type | Buffer System | pH | Salt (mM) | Divalent Cation (mM) | Nucleotide (mM) | Other Additives | Reference |
| ATPase Activity | 30 mM HEPES-KOH | 7.8 | 150 NaCl | 2 MgCl₂ | 20 µM ATP | - | [2] |
| Substrate Binding (FP) | 50 mM HEPES | 7.5 | 100 KCl | 2 MgCl₂ | 1 ADP | 0.01% Tween-20 | [1] |
| Substrate Binding (ITC) | 20 mM HEPES | 7.5 | 100 NaCl | 2 MgCl₂ | 1 ADP | - | [1] |
| Protein Stability | 20 mM HEPES | 7.5 | 300 NaCl | - | - | 10% glycerol, 10 mM DTT |
Mandatory Visualization
Unfolded Protein Response (UPR) Signaling Pathway
Under normal conditions, BiP is bound to the luminal domains of three ER stress sensors: IRE1 (inositol-requiring enzyme 1), PERK (PKR-like ER kinase), and ATF6 (activating transcription factor 6), keeping them in an inactive state. Upon accumulation of unfolded proteins in the ER, BiP preferentially binds to these unfolded proteins, leading to its dissociation from the stress sensors. This dissociation triggers the activation of the UPR pathways to restore ER homeostasis.
The Unfolded Protein Response (UPR) signaling pathway initiated by BiP dissociation.
Experimental Protocols
BiP ATPase Activity Assay (Malachite Green-based)
This protocol measures the rate of ATP hydrolysis by quantifying the release of inorganic phosphate (Pi).[8]
Materials:
-
Purified BiP protein
-
Assay Buffer: 30 mM HEPES-KOH, pH 7.8, 150 mM NaCl[2]
-
10 mM ATP solution
-
100 mM MgCl₂ solution
-
Substrate of interest (optional)
-
Malachite Green reagent
-
Phosphate standard solution
-
96-well microplate
Procedure:
-
Prepare a phosphate standard curve: Create a series of dilutions of the phosphate standard in the assay buffer.
-
Reaction Setup: In a 96-well plate, prepare the reaction mixtures. Include the following controls:
-
No-Enzyme Control: All components except BiP, to measure non-enzymatic ATP hydrolysis.
-
No-Substrate Control: BiP and all other components except the substrate, to measure basal ATPase activity.
-
-
Initiate the Reaction: Pre-incubate the plate at the desired temperature (e.g., 37°C). Start the reaction by adding ATP to each well.
-
Incubation: Incubate the plate for a set period (e.g., 30-60 minutes), or take time points for a kinetic assay.
-
Stop and Detect: Stop the reaction by adding the Malachite Green reagent to all wells. This reagent is acidic and will terminate the enzymatic reaction.[8]
-
Read Absorbance: After a short incubation at room temperature to allow color development, read the absorbance at ~620 nm.
-
Calculate Activity: Subtract the absorbance of the no-enzyme control. Use the phosphate standard curve to determine the amount of phosphate released. Calculate the specific activity of BiP (e.g., in nmol Pi/min/mg BiP).
BiP Substrate Binding Assay (Fluorescence Polarization)
This assay measures the binding of a fluorescently labeled substrate to BiP.[1][9]
Materials:
-
Purified BiP protein
-
Fluorescently labeled substrate (e.g., a peptide with a FITC label)
-
Binding Buffer: 50 mM HEPES, pH 7.5, 100 mM KCl, 2 mM MgCl₂, 1 mM ADP, 0.01% Tween-20[1]
-
Black, low-volume 384-well plate
Procedure:
-
Prepare Serial Dilution of BiP: Prepare a 2x serial dilution of BiP in the binding buffer.
-
Prepare Labeled Substrate: Prepare a 2x solution of the fluorescently labeled substrate at a concentration well below the expected dissociation constant (Kd) (e.g., 2-20 nM).
-
Assay Setup:
-
Add 20 µL of the 2x BiP dilutions to the wells of the 384-well plate.
-
For "no protein" controls, add 20 µL of binding buffer.
-
Initiate the binding reaction by adding 20 µL of the 2x labeled substrate solution to all wells.
-
-
Incubation: Incubate the plate at room temperature for 30-60 minutes to reach equilibrium.
-
Measure Polarization: Measure the fluorescence polarization using a plate reader equipped with appropriate filters for the fluorophore.
-
Data Analysis: Plot the millipolarization (mP) values against the BiP concentration and fit the data to a one-site binding model to determine the Kd.
Troubleshooting Guides
Troubleshooting Low BiP ATPase Activity
| Problem | Possible Cause(s) | Suggested Solution(s) |
| Low or no ATPase activity | 1. Inactive BiP enzyme (degradation, aggregation).2. Incorrect protein concentration.3. Suboptimal buffer conditions (pH, ionic strength).4. Inactive ATP or divalent cation solution. | 1. Check BiP integrity on an SDS-PAGE gel. Use fresh aliquots stored at -80°C.[8]2. Verify protein concentration using a reliable method (e.g., BCA assay).3. Optimize pH (7.0-8.0) and salt concentration (50-150 mM). Ensure Mg²⁺ is present at an optimal concentration (e.g., 2 mM).[1][2]4. Prepare fresh ATP and MgCl₂ solutions. |
| High background signal (no-enzyme control) | 1. Spontaneous ATP hydrolysis.2. Phosphate contamination in reagents. | 1. Prepare ATP stock fresh and store on ice.2. Use high-purity water and reagents. Test individual reagents for phosphate contamination. |
| Inconsistent results between replicates | 1. Pipetting errors.2. Temperature fluctuations.3. Reagent instability. | 1. Use calibrated pipettes and ensure proper mixing.2. Pre-incubate all reagents and plates to the assay temperature.[8]3. Prepare detection reagents fresh for each experiment. |
Troubleshooting BiP Substrate Binding Assays (Fluorescence Polarization)
| Problem | Possible Cause(s) | Suggested Solution(s) |
| Low polarization signal change | 1. Labeled substrate is too large relative to BiP.2. Low binding affinity.3. Insufficient BiP concentration. | 1. Ensure the labeled molecule is significantly smaller than BiP.[1]2. Optimize buffer conditions (pH, salt) to enhance binding. Ensure ADP is included to stabilize the high-affinity state.3. Increase the concentration of BiP to achieve saturation. |
| No saturation observed at high protein concentrations | 1. Non-specific binding of the labeled substrate.2. Protein aggregation at high concentrations. | 1. Add a non-ionic detergent (e.g., 0.01% Tween-20) to the buffer.[1]2. Include a reducing agent (e.g., DTT) and/or glycerol to improve BiP stability. Confirm BiP is not aggregated using techniques like dynamic light scattering (DLS). |
| High variability between wells | 1. Pipetting inaccuracies.2. Bubbles in the wells.3. Labeled substrate sticking to the plate. | 1. Use a multichannel pipette for consistency.2. Centrifuge the plate briefly before reading.3. Include a non-ionic detergent in the buffer. |
References
- 1. benchchem.com [benchchem.com]
- 2. ATPase activity of human binding immunoglobulin protein (BiP) variants is enhanced by signal sequence and physiological concentrations of Mn2+ - PMC [pmc.ncbi.nlm.nih.gov]
- 3. benchchem.com [benchchem.com]
- 4. benchchem.com [benchchem.com]
- 5. Unlocking the Chemistry: HEPES vs. Tris Buffers - Choosing the Right Solution for Your Lab - Blog - Hopax Fine Chemicals [hopaxfc.com]
- 6. TRIS,phosphate,HEPES...... which one is the best for your experiments? [yacooscience.com]
- 7. researchgate.net [researchgate.net]
- 8. benchchem.com [benchchem.com]
- 9. benchchem.com [benchchem.com]
Common experimental errors with Bicep and solutions
Welcome to the Bicep Technical Support Center. This resource is designed for researchers, scientists, and drug development professionals who utilize Bayesian Inference of Conformational Populations (this compound) in their experimental workflows. Here you will find troubleshooting guides and frequently asked questions to address common issues encountered during the application of the this compound algorithm to reconcile theoretical models with experimental data.
Frequently Asked Questions (FAQs)
Q1: What is the this compound algorithm and what is its primary application in research?
The Bayesian Inference of Conformational Populations (this compound) algorithm is a computational method used to refine theoretical models of molecular conformations by incorporating experimental data.[1][2] In essence, it provides a statistically rigorous way to determine the different shapes (conformations) a molecule, such as a peptide or a potential drug candidate, adopts in solution. This is crucial in drug development for understanding how a molecule's shape influences its function and interactions with biological targets.
Q2: What are the most common sources of error when using the this compound algorithm?
Common errors in this compound applications often stem from the input data and the inherent assumptions of the model. These can be broadly categorized as:
-
Inaccurate Prior Information: The initial set of molecular conformations, typically generated from molecular dynamics simulations, may not be accurate due to limitations in the force field used.[1]
-
Noisy or Sparse Experimental Data: While this compound is designed to handle such data, significant noise or a lack of sufficient experimental restraints can lead to a poorly refined conformational ensemble.[2]
-
Forward Model Inaccuracies: The "forward model," which calculates the expected experimental observables from a given conformation, may not perfectly represent the true physical reality.
-
Conceptual Discrepancy: A key conceptual challenge is that the likelihood function in this compound often compares experimental data, which is an average over an entire ensemble of molecules, to individual conformational states.[2]
Q3: My this compound analysis results in a conformational ensemble that still doesn't match my experimental data well. What could be the issue?
This common problem can arise from several sources. A primary reason could be the quality of the initial conformational ensemble (the prior). If the force field used in the initial simulations is not well-suited for your molecule, the resulting conformations may be physically unrealistic, and this compound may struggle to correct them sufficiently.[1] Another possibility is that the experimental data itself is noisy or contains systematic errors that are not accounted for. Finally, the parameters of the forward model used to back-calculate experimental observables from the structures might be inaccurate.
Troubleshooting Guides
Issue 1: Poor Agreement Between this compound-Refined Ensemble and Experimental Data
Symptoms:
-
High Chi-squared values or poor correlation between back-calculated and experimental observables.
-
The this compound score, a metric for model quality, does not significantly improve after reweighting.[2]
Possible Causes and Solutions:
| Cause | Solution |
| Inaccurate Force Field | Use the this compound score to test multiple force fields and select the one that provides the best agreement with the experimental data before reweighting.[2] |
| Noisy Experimental Data | Re-examine the experimental data for outliers or systematic errors. If possible, acquire additional, higher-quality data to provide more robust restraints. |
| Inaccurate Forward Model Parameters | If using a forward model with adjustable parameters (e.g., for calculating NMR chemical shifts), consider optimizing these parameters. Some advanced implementations of this compound are exploring automatic forward model parameterization. |
| Insufficient Sampling in Prior Simulation | Ensure that the initial molecular dynamics simulation has been run long enough to explore a wide range of relevant conformations. |
Issue 2: Overfitting of the Conformational Ensemble to Noisy Data
Symptoms:
-
The reweighted ensemble shows very few dominant conformations that perfectly match the (potentially noisy) experimental data, which may not be physically realistic.
-
The uncertainty in the reweighted populations is very low, suggesting overconfidence in the result.
Possible Causes and Solutions:
| Cause | Solution |
| Sparse and/or Noisy Experimental Restraints | This compound is designed for this scenario, but it's crucial to use conservative reference potentials that do not make overly strong assumptions about the underlying distributions of the data.[2] |
| Conceptual Problem of Single State vs. Ensemble Average | A key conceptual issue with this compound is comparing ensemble-averaged experimental data to individual conformations.[2] An advanced solution being developed is "replica averaging," which aims to compare ensemble predictions to the experimental data directly.[1] For current use, being aware of this limitation is important for interpreting the results. |
Experimental and Computational Protocols
Protocol: A Typical this compound Workflow for Refining a Peptide Conformational Ensemble
This protocol outlines the key steps for using this compound to refine a conformational ensemble of a peptide based on NMR experimental data.
1. Generation of the Prior Conformational Ensemble:
- Perform a molecular dynamics (MD) simulation of the peptide using a chosen force field (e.g., AMBER, CHARMM).
- Run the simulation for a sufficient time to ensure thorough sampling of the conformational space.
- Cluster the MD trajectory to obtain a set of representative discrete conformational states and their initial populations (the prior).
2. Acquisition of Experimental Data:
- Experimentally measure relevant NMR observables for the peptide, such as Nuclear Overhauser Effects (NOEs), J-couplings, and chemical shifts.
3. This compound Calculation Setup:
- Prepare the input files for the this compound software. This includes the prior conformational ensemble (structures and populations) and the experimental restraints.
- Define the forward model that will be used to calculate the NMR observables from the atomic coordinates of the conformations.
4. Running the this compound Reweighting:
- Execute the this compound algorithm. This will typically involve a Markov Chain Monte Carlo (MCMC) simulation to sample the posterior distribution of conformational populations.
- The output will be a new set of weights for each conformation in the prior ensemble, representing the this compound-refined posterior distribution.
5. Analysis of the Results:
- Analyze the reweighted conformational ensemble. Identify the major conformations and their populations.
- Compare the back-calculated observables from the reweighted ensemble with the experimental data to assess the goodness of fit.
- Evaluate the this compound score to quantify the improvement of the model.
Visualizations
Caption: A typical experimental workflow for using the this compound algorithm.
Caption: Logical relationship for troubleshooting poor model-experiment agreement.
References
Validation & Comparative
Comparative Efficacy Analysis: SLU-PP-332 versus BPC-157 in Muscle Enhancement and Repair
This guide provides a comparative analysis of two novel compounds, SLU-PP-332 and BPC-157, which have demonstrated potential in modulating muscle physiology. The information is intended for researchers, scientists, and professionals in drug development interested in therapeutic agents for muscle growth, repair, and performance enhancement.
Compound Overview
SLU-PP-332: An "exercise mimetic" compound that has been shown in preclinical studies to stimulate metabolic pathways that are typically activated during physical exercise.[1][2] It functions by activating estrogen-related receptors (ERRs), which play a crucial role in regulating exercise-induced stress adaptation and other physiological processes within the muscle.[3][4]
BPC-157: A body protection compound, this pentadecapeptide is a naturally occurring peptide found in gastric juice.[5] Preclinical research suggests it has regenerative capabilities, promoting the healing of various tissues, including muscle, tendon, and ligament.[5]
Efficacy Data Comparison
The following table summarizes the key efficacy findings for SLU-PP-332 and BPC-157 based on available preclinical data.
| Efficacy Parameter | SLU-PP-332 | BPC-157 | Source |
| Primary Mechanism | ERR Agonist (Exercise Mimetic) | Growth Hormone Receptor Expression, Angiogenesis, Anti-inflammatory | [3][4][5] |
| Effect on Muscle Fiber | Increased fatigue-resistant muscle fibers | Improved muscle structure and myofibril diameter | [3][5] |
| Effect on Endurance | Increased running endurance in mice (ran nearly 50% further) | Not explicitly studied for endurance enhancement | [1] |
| Effect on Metabolism | Shifts metabolism to utilize fatty acids | Not a primary reported effect | [1][2] |
| Effect on Muscle Injury | Not a primary focus of reported studies | Improved functional, structural, and biomechanical outcomes in muscle transection and crush models | [5] |
| Effect on Weight | Led to weight loss in obese mice without affecting appetite | Not a primary reported effect | [1] |
Experimental Protocols
SLU-PP-332 Endurance Study in Mice:
-
Subjects: Normal-weight mice.
-
Treatment: Administration of SLU-PP-332.
-
Experiment: Mice were subjected to endurance testing on a rodent treadmill.
-
Primary Outcome: Measurement of running time and distance until exhaustion.
-
Results: Mice treated with SLU-PP-332 ran for a significantly longer duration and distance compared to the control group.[1]
BPC-157 Muscle Injury Model in Rats:
-
Subjects: Rats with induced muscle injuries (transection and crush models).
-
Treatment: Administration of BPC-157.
-
Experiment: Evaluation of muscle healing and functional recovery over time.
-
Primary Outcomes: Assessment of load to failure, motor function indices, muscle myofibril and macroscopic diameters, and reduction in atrophy.
-
Results: BPC-157 treatment led to improved structural, functional, and biomechanical properties of the injured muscle compared to controls.[5]
Visualizing Molecular Pathways and Experimental Logic
To further elucidate the mechanisms and applications of these compounds, the following diagrams illustrate their respective signaling pathways and the logical flow of a comparative in-vivo study.
Caption: SLU-PP-332 signaling cascade.
Caption: BPC-157's proposed healing mechanism.
References
- 1. Exercise-mimicking drug sheds weight, boosts muscle activity in mice News | University of Florida [news.ufl.edu]
- 2. sciencealert.com [sciencealert.com]
- 3. news-medical.net [news-medical.net]
- 4. acs.org [acs.org]
- 5. Emerging Use of BPC-157 in Orthopaedic Sports Medicine: A Systematic Review - PMC [pmc.ncbi.nlm.nih.gov]
A Comparative Analysis of Bicyclic Peptides and Their Therapeutic Analogs
In the landscape of modern drug development, the quest for therapeutic modalities that combine high specificity and potency with favorable pharmacokinetic properties is paramount. Bicyclic peptides have emerged as a promising class of drugs, bridging the gap between small molecules and large biologics. This guide provides a comparative analysis of bicyclic peptides, represented by the clinical-stage Bicycle Drug Conjugate (BDC) BT1718, with its therapeutic analogs: a function-blocking monoclonal antibody and a small molecule inhibitor, both targeting the same cancer-associated protein, Membrane Type 1 Matrix Metalloproteinase (MT1-MMP).
Data Presentation: A Quantitative Comparison
The following tables summarize key quantitative data for each therapeutic modality, offering a side-by-side comparison of their performance characteristics.
Table 1: Target Binding and In Vitro Potency
| Parameter | Bicyclic Peptide (BT1718) | Monoclonal Antibody (DX-2400) | Small Molecule (Marimastat) |
| Target | MT1-MMP (MMP-14) | MT1-MMP (MMP-14) | Multiple MMPs (including MMP-1, -2, -3, -7, -9, -12, -14) |
| Binding Affinity (KD) | ~3-5 nM[1][2] | ~0.6 nM (Ki)[3] | IC50 values in low nM range for various MMPs[4] |
| Specificity | High for MT1-MMP[1] | High for MT1-MMP[3] | Broad-spectrum MMP inhibitor[4] |
| In Vitro Cytotoxicity | Dose-dependent killing of MT1-MMP expressing cells[2] | Inhibition of MT1-MMP mediated cellular functions[3] | Inhibition of MMP-dependent processes |
Table 2: Pharmacokinetic Properties
| Parameter | Bicyclic Peptide (BT1718) | Monoclonal Antibody | Small Molecule (Marimastat) |
| Molecular Weight | ~2 kDa (peptide) | ~150 kDa | <1 kDa |
| Terminal Half-life (t1/2) | ~0.2 - 0.5 hours[5][6] | Days to weeks | ~4-10 hours[4][7] |
| Clearance Mechanism | Renal | Primarily via intracellular catabolism | Hepatic metabolism and renal excretion |
| Tumor Penetration | Rapid and deep[5][6] | Slow and often limited to perivascular regions | Variable, depends on physicochemical properties |
| Volume of Distribution (Vss) | ~12.5 L[5] | Confined to plasma and extracellular fluid | Wider distribution |
Experimental Protocols
Detailed methodologies for the key experiments cited are crucial for the interpretation and replication of the presented data.
Surface Plasmon Resonance (SPR) for Binding Affinity
Objective: To determine the binding affinity (KD), and association (ka) and dissociation (kd) rates of a therapeutic molecule to its target protein.
Methodology:
-
Immobilization: The target protein (e.g., recombinant human MT1-MMP) is immobilized on a sensor chip surface. Common surfaces include carboxymethylated dextran (CM5).
-
Analyte Preparation: The therapeutic molecule (bicyclic peptide, monoclonal antibody, or small molecule) is prepared in a series of concentrations in a suitable running buffer.
-
Association: The analyte solutions are injected over the sensor surface at a constant flow rate for a defined period, allowing for binding to the immobilized target. The change in the SPR signal, measured in response units (RU), is monitored in real-time.
-
Dissociation: After the association phase, the running buffer is flowed over the chip to monitor the dissociation of the analyte from the target.
-
Regeneration: A regeneration solution is injected to remove any remaining bound analyte, preparing the sensor surface for the next cycle.
-
Data Analysis: The resulting sensorgrams are fitted to a suitable binding model (e.g., 1:1 Langmuir binding) to calculate the kinetic parameters (ka, kd) and the equilibrium dissociation constant (KD = kd/ka).
In Vitro Cytotoxicity Assay (MTT/AlamarBlue)
Objective: To assess the ability of a therapeutic agent to induce cell death in cancer cell lines.
Methodology:
-
Cell Seeding: Cancer cells expressing the target of interest (e.g., HT-1080 cells for MT1-MMP) are seeded in 96-well plates and allowed to adhere overnight.
-
Compound Treatment: The cells are treated with serial dilutions of the therapeutic agent (e.g., BT1718) or vehicle control.
-
Incubation: The plates are incubated for a specified period (e.g., 72 hours) to allow the compound to exert its effect.
-
Viability Assessment: A viability reagent such as MTT (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) or AlamarBlue is added to each well. Metabolically active cells reduce the reagent, resulting in a colorimetric or fluorometric change.
-
Data Acquisition: The absorbance or fluorescence is measured using a microplate reader.
-
Data Analysis: The percentage of cell viability is calculated relative to the untreated control cells. The half-maximal inhibitory concentration (IC50) is determined by plotting cell viability against the logarithm of the drug concentration and fitting the data to a dose-response curve.
In Vivo Efficacy in Xenograft Mouse Models
Objective: To evaluate the anti-tumor efficacy of a therapeutic agent in a living organism.
Methodology:
-
Cell Implantation: Human cancer cells (e.g., from a cell line or a patient-derived xenograft) are subcutaneously implanted into immunodeficient mice.
-
Tumor Growth and Randomization: Tumors are allowed to grow to a palpable size. The mice are then randomized into treatment and control groups.
-
Treatment Administration: The therapeutic agent is administered to the treatment group according to a specific dosing schedule and route of administration (e.g., intravenous for BT1718). The control group receives a vehicle.
-
Monitoring: Tumor volume and the body weight of the mice are measured regularly throughout the study.
-
Endpoint: The study is concluded when the tumors in the control group reach a predetermined size, or at a specified time point.
-
Data Analysis: Tumor growth inhibition is calculated by comparing the average tumor volume in the treated group to the control group. Statistical analysis is performed to determine the significance of the observed anti-tumor effect.
Mandatory Visualizations
Signaling Pathway
Caption: MT1-MMP signaling pathway in cancer progression.
Experimental Workflow
Caption: General experimental workflow for preclinical drug evaluation.
Logical Relationship of Therapeutic Modalities
References
- 1. bicycletherapeutics.com [bicycletherapeutics.com]
- 2. bicycletherapeutics.com [bicycletherapeutics.com]
- 3. Selective function-blocking monoclonal human antibody highlights the important role of membrane type-1 matrix metalloproteinase (MT1-MMP) in metastasis - PMC [pmc.ncbi.nlm.nih.gov]
- 4. Results of single and repeat dose studies of the oral matrix metalloproteinase inhibitor marimastat in healthy male volunteers - PMC [pmc.ncbi.nlm.nih.gov]
- 5. Bicycle Therapeutics Announces Presentation of Updated Data from Phase I/IIa Trial Evaluating BT1718 in Patients with Advanced Solid Tumors at ESMO 2019 Annual Congress - BioSpace [biospace.com]
- 6. adcreview.com [adcreview.com]
- 7. Phase I trial of Marimastat, a novel matrix metalloproteinase inhibitor, administered orally to patients with advanced lung cancer - PubMed [pubmed.ncbi.nlm.nih.gov]
Navigating the Landscape of High-Throughput Proteomics: A Comparative Guide to Leading Platforms
An objective analysis of major proteomics technologies to guide researchers in selecting the optimal platform for their experimental needs. This guide synthesizes cross-platform validation data, offering insights into performance, reproducibility, and experimental considerations.
The term "Bicep" in the context of a specific, widely recognized proteomics platform remains ambiguous in current scientific literature. It is possible this refers to a proprietary in-house system, a novel technology not yet broadly published, or a misnomer for an existing platform. However, the core need for cross-laboratory and cross-platform validation of proteomic effects is a critical concern for researchers. This guide therefore addresses the user's request by providing a comprehensive comparison of the leading high-throughput proteomics technologies currently utilized across different laboratories: Mass Spectrometry (MS)-based platforms, Olink's Proximity Extension Assay (PEA), and SomaLogic's SomaScan.
Performance Comparison of Major Proteomics Platforms
The selection of a proteomics platform is a critical decision in experimental design, with significant implications for data quality, scope, and biological interpretation. The following tables summarize quantitative data from studies comparing the performance of Mass Spectrometry, Olink, and SomaScan platforms, providing a clear overview of their respective strengths and weaknesses.
| Platform | Proteome Coverage (Number of Proteins Detected) | Median Technical CV (%) | Data Completeness (%) | FDA-approved Biomarkers Covered (%) |
| SomaScan 11K | 9,645 | 5.3 | 96.2 | 88 |
| SomaScan 7K | 6,401 | 5.8 | 95.8 | 76 |
| Olink 5K | ~5,000 | 26.8 (12.4 after filtering) | 35.9 | Not Specified |
| Olink 3K | ~3,000 | 11.4 | Not Specified | Not Specified |
| MS-Nanoparticle | >13,000 (in some studies) | 26.4 | Not Specified | Not Specified |
| MS-HAP Depletion | Not Specified | 29.8 | Not Specified | Not Specified |
| MS-IS Targeted | Targeted | 8.3 | Not Specified | Not Specified |
CV: Coefficient of Variation, a measure of precision. Data synthesized from a comparative study of plasma proteomics platforms.[1][2]
| Platform Comparison | Average Correlation (r-value) | Key Considerations |
| SomaScan vs. Olink | 0.46 | Bimodal distribution of correlations, with about half of the protein pairs showing good to excellent correlation (r≥0.5) and the other half showing poor correlation (r<0.5).[3] |
| SomaScan vs. Targeted Immunoassays | Variable | 6 out of 18 assays showed good correlation (r≥0.8), while 10 were poorly correlated (r<0.5).[3] |
| Affinity-based vs. MS-based | Variable | Targeted MS with internal standards (MS-IS Targeted) showed the highest correlation with an affinity-based platform (r=0.62 with Olink 3K).[2] |
Experimental Protocols
Reproducibility and cross-laboratory validation are contingent on detailed and standardized experimental protocols. Below are generalized methodologies for key proteomics experiments based on common practices.
Plasma Proteome Profiling Workflow
A typical workflow for plasma proteomics analysis, whether using affinity-based or MS-based methods, involves several key steps from sample collection to data analysis. The goal is to ensure consistency and minimize pre-analytical variability.
References
Clarification Required: The Term "Bicep" in a Therapeutic Context is Ambiguous
To provide a comprehensive and accurate comparison guide as requested, clarification is needed regarding the term "Bicep." Initial research across medical and pharmaceutical databases does not yield a recognized therapeutic agent, drug, or technology platform under this name. The term predominantly refers to the biceps brachii muscle in the arm.
It is possible that "this compound" is an internal project name, a novel modality not yet in the public domain, or an acronym specific to a particular field of research. Given the audience of researchers, scientists, and drug development professionals, precision is paramount.
One potential interpretation, based on the sound of the word, is that "this compound" could be related to Bispecific T-cell Engager (BiTE®) therapies . BiTEs are a class of artificial bispecific monoclonal antibodies designed to direct a patient's T-cells to target and eliminate tumor cells.[1][2][3] This is a rapidly evolving area of cancer immunotherapy with several approved drugs and many more in development.[2][3][4][5]
To proceed with generating the requested comparison guide, please provide the following information:
-
Full Name and Nature of "this compound": Is it a specific molecule, a technology platform, or an acronym? If it is an acronym, please provide its full name.
-
Therapeutic Indication: What specific disease or condition is "this compound" intended to treat? (e.g., B-cell acute lymphoblastic leukemia, non-Hodgkin's lymphoma, a specific solid tumor).
-
Mechanism of Action: How does "this compound" work on a biological level?
Once this essential information is provided, a detailed and accurate comparison to the relevant standard-of-care treatments can be developed, complete with the requested data tables, experimental protocols, and visualizations.
For example, if "this compound" were a hypothetical BiTE therapy targeting CD19 for the treatment of relapsed or refractory B-cell acute lymphoblastic leukemia (ALL), the standard-of-care for comparison might include therapies like blinatumomab (a CD19-directed BiTE) or CAR-T cell therapies.[2][4] A guide would then be constructed comparing their efficacy, safety profiles, and the experimental methodologies used in pivotal clinical trials.
References
A Head-to-Head Comparison of Bicep with Other EGFR Inhibitors
A Guide for Researchers, Scientists, and Drug Development Professionals
Disclaimer: The term "Bicep" does not correspond to a recognized inhibitor in publicly available scientific literature. This guide uses "this compound" as a placeholder for a hypothetical, third-generation Epidermal Growth Factor Receptor (EGFR) inhibitor. The data presented for comparison involves established first- and third-generation EGFR inhibitors, Gefitinib and Osimertinib, respectively, to provide a framework for evaluating a novel agent like "this compound".
Introduction
The Epidermal Growth Factor Receptor (EGFR) signaling pathway is a cornerstone in regulating cell proliferation, survival, and differentiation.[1][2] Its dysregulation, often through activating mutations, is a key driver in the pathogenesis of various cancers, most notably non-small cell lung cancer (NSCLC).[3][4] This has led to the development of EGFR tyrosine kinase inhibitors (TKIs) as a primary therapeutic strategy.[5]
First-generation TKIs, such as Gefitinib, are reversible inhibitors that compete with ATP at the catalytic site of the EGFR kinase domain.[3] While effective against sensitizing mutations (e.g., Exon 19 deletions and L858R), their efficacy is often limited by the emergence of resistance, most commonly through the T790M "gatekeeper" mutation.[3]
Third-generation TKIs, exemplified by Osimertinib, were designed to overcome this resistance.[3][6] These are irreversible inhibitors that form a covalent bond with a specific cysteine residue (C797) in the ATP-binding pocket of the EGFR kinase, providing potent inhibition of both sensitizing and T790M resistance mutations while sparing wild-type (WT) EGFR.[3][6][7] This guide provides a comparative analysis of a hypothetical third-generation inhibitor, "this compound," against Gefitinib and Osimertinib.
Mechanism of Action
Gefitinib is a reversible, ATP-competitive inhibitor of the EGFR tyrosine kinase.[3][8] This inhibition prevents EGFR autophosphorylation and subsequent activation of downstream pro-survival signaling pathways.[3][8]
Osimertinib and the hypothetical "this compound" are third-generation, irreversible EGFR TKIs.[3][9] They selectively target both EGFR-sensitizing and T790M resistance mutations by forming a covalent bond with the C797 residue in the ATP-binding site.[6][7] This mechanism leads to sustained inhibition of mutant EGFR, while having significantly less activity against WT-EGFR, which is believed to contribute to a more favorable safety profile.[8][10]
Signaling Pathway and Point of Inhibition
Upon ligand binding (e.g., EGF), EGFR dimerizes and undergoes autophosphorylation, activating multiple downstream signaling cascades, primarily the RAS-RAF-MEK-ERK (MAPK) and the PI3K-AKT-mTOR pathways, which are crucial for cell proliferation and survival.[11][12] Both first- and third-generation inhibitors act by blocking the kinase activity of EGFR, thereby preventing the initiation of these downstream signals.[8]
Caption: Simplified EGFR signaling pathway and inhibitor targets.
Comparative Efficacy: In Vitro Data
The potency of EGFR inhibitors is typically assessed by determining their half-maximal inhibitory concentration (IC50) against various EGFR-mutant cell lines. A lower IC50 value indicates greater potency. Third-generation inhibitors are characterized by their high potency against the T790M resistance mutation, a key weakness of first-generation agents.[3][6]
Table 1: In Vitro Inhibitory Activity (IC50, nM)
| Cell Line | EGFR Mutation Status | Gefitinib (IC50, nM) | Osimertinib (IC50, nM) | [this compound] (IC50, nM) |
|---|---|---|---|---|
| PC9 | Exon 19 deletion | ~10-20[13] | <15[13] | Data Placeholder |
| H1975 | L858R/T790M | >5000[13] | <15[6][13] | Data Placeholder |
| WT EGFR | Wild-Type | Variable | ~480-1865[6] | Data Placeholder |
Comparative Efficacy: Clinical Data
Head-to-head clinical trials are the definitive measure of an inhibitor's efficacy and safety. The FLAURA trial is a pivotal Phase III study that compared Osimertinib with standard-of-care (SoC) first-generation EGFR-TKIs (Gefitinib or Erlotinib) in the first-line treatment of EGFR-mutated advanced NSCLC.[8]
Table 2: Clinical Trial Efficacy Data (FLAURA Trial - First-Line Treatment)
| Endpoint | Gefitinib / Erlotinib | Osimertinib | Hazard Ratio (95% CI) | p-value |
|---|---|---|---|---|
| Median Progression-Free Survival (PFS) | 10.2 months[13] | 18.9 months[13] | 0.46 (0.37-0.57)[13] | <0.001[13] |
| Median Overall Survival (OS) | 31.8 months[13] | 38.6 months[13] | 0.799 (0.641-0.997)[13] | 0.0462[13] |
| Objective Response Rate (ORR) | 76%[13] | 80%[13] | - | - |
| Median Duration of Response | 8.5 months[13] | 17.2 months[13] | - | - |
Experimental Protocols
In Vitro Kinase Assay (Biochemical)
Objective: To determine the direct inhibitory activity of a compound against purified EGFR kinase domains (wild-type and mutant).
Methodology (Illustrative Example: TR-FRET Assay): [14]
-
Reagent Preparation: Prepare kinase buffer, recombinant human EGFR kinase domain (WT, L858R, T790M, etc.), a biotinylated peptide substrate, and ATP. Prepare serial dilutions of test inhibitors (this compound, Osimertinib, Gefitinib).[14]
-
Assay Procedure:
-
Add diluted test compounds to a low-volume 384-well plate.[14]
-
Add the EGFR enzyme solution and incubate briefly.[14]
-
Initiate the kinase reaction by adding the substrate/ATP solution. Incubate for 60 minutes at room temperature.[14]
-
Stop the reaction by adding a detection solution containing EDTA, a europium-labeled anti-phosphotyrosine antibody, and streptavidin-allophycocyanin (SA-APC).[14]
-
-
Data Acquisition: Read the plate on a TR-FRET-compatible plate reader. The ratio of emission at 665 nm (APC) to 620 nm (europium) is proportional to the extent of substrate phosphorylation.[14]
-
Data Analysis: Calculate percent inhibition relative to controls and plot against inhibitor concentration to determine the IC50 value.
Cell-Based Proliferation Assay
Objective: To assess the effect of an inhibitor on the proliferation and viability of cancer cells harboring specific EGFR mutations.
Methodology (Illustrative Example: CellTiter-Glo® Luminescent Cell Viability Assay): [14][15]
-
Cell Seeding: Seed EGFR-mutant NSCLC cells (e.g., PC9, H1975) in 96-well plates and allow them to attach overnight.
-
Compound Treatment: Treat cells with serial dilutions of the test inhibitors.[14] Include vehicle (DMSO) as a negative control.
-
Incubation: Incubate the plates for 72 hours at 37°C in a 5% CO₂ incubator.[14]
-
Viability Assessment:
-
Data Acquisition: Measure luminescence using a plate reader.[14]
-
Data Analysis: Normalize the data to the vehicle-treated cells (100% viability). Plot the normalized viability versus the logarithm of the compound concentration and fit the data to a dose-response curve to determine the GI₅₀ (concentration for 50% growth inhibition).[14]
Caption: General workflow for inhibitor characterization.
Conclusion
The evolution from first- to third-generation EGFR inhibitors represents a significant advancement in targeted cancer therapy, driven by a deeper understanding of resistance mechanisms. A novel third-generation inhibitor like "this compound" would be expected to demonstrate a profile similar to Osimertinib: potent activity against both sensitizing and T790M resistance mutations, a high degree of selectivity over wild-type EGFR, and superior clinical efficacy in terms of progression-free and overall survival compared to first-generation agents. The experimental frameworks provided here offer a robust starting point for the preclinical and clinical evaluation of any new therapeutic candidate in this class.
References
- 1. A comprehensive pathway map of epidermal growth factor receptor signaling - PMC [pmc.ncbi.nlm.nih.gov]
- 2. creative-diagnostics.com [creative-diagnostics.com]
- 3. benchchem.com [benchchem.com]
- 4. aacrjournals.org [aacrjournals.org]
- 5. Comparison of Gefitinib in the treatment of patients with non-small cell lung cancer and clinical effects of Osimertinib and EGFR Gene mutation - PMC [pmc.ncbi.nlm.nih.gov]
- 6. Osimertinib in the treatment of non-small-cell lung cancer: design, development and place in therapy - PMC [pmc.ncbi.nlm.nih.gov]
- 7. What is the mechanism of action of Osimertinib mesylate? [synapse.patsnap.com]
- 8. benchchem.com [benchchem.com]
- 9. What is the mechanism of Osimertinib mesylate? [synapse.patsnap.com]
- 10. Mechanism of Action – TAGRISSO® (osimertinib) [tagrissohcp.com]
- 11. lifesciences.danaher.com [lifesciences.danaher.com]
- 12. ClinPGx [clinpgx.org]
- 13. benchchem.com [benchchem.com]
- 14. benchchem.com [benchchem.com]
- 15. Construction of a novel cell-based assay for the evaluation of anti-EGFR drug efficacy against EGFR mutation - PMC [pmc.ncbi.nlm.nih.gov]
Unraveling "Bicep": A Clarification on Terminology in Biological Target Validation
In the dynamic landscape of drug discovery and biomedical research, precise terminology is paramount. Our investigation into a product or technology named "Bicep" for the validation of biological target specificity has revealed that this term does not correspond to a recognized, specific experimental tool or platform within the life sciences community. The term "this compound" is associated with several distinct entities in other scientific and technical fields, which can lead to confusion.
Our findings indicate the following applications of the term "this compound" or its variations:
-
BICEPS: A European-based research consortium dedicated to advancing the understanding of Parkinson's disease by focusing on the immune system and utilizing systems biology and artificial intelligence. This is a collaborative research initiative rather than a specific commercial product for target validation.
-
BICEPP: A computational, statistical text-mining tool designed to predict the characteristics of drugs by analyzing MEDLINE abstracts. This is a bioinformatics approach and not a laboratory-based experimental method for target validation.
-
BICePs: A computational algorithm, "Bayesian Inference of Conformational Populations," which is used in molecular modeling to reconcile simulation data with experimental results, particularly for understanding the structures of molecules like peptidomimetics.
-
This compound: An internal designation for a "Biologics Characterization, Expression, and Purification" group within the pharmaceutical company Sanofi.
Furthermore, "this compound" is widely recognized as the name of a domain-specific language developed by Microsoft for deploying Azure resources, a context entirely separate from biological research.
Given the absence of a specific biological tool named "this compound" for target validation, we are unable to provide a direct product comparison as initially requested.
However, to address the core need for a comprehensive guide to validating the specificity of biological targets, we have pivoted to a comparison of established and cutting-edge technologies that are central to modern drug discovery. This guide will provide researchers, scientists, and drug development professionals with a clear overview of the available methods, their principles, and their relative strengths and weaknesses.
A Comparative Guide to Validating Biological Target Specificity: Key Technologies and Methodologies
Validating that a potential therapeutic agent interacts specifically with its intended biological target is a critical step in drug development. This process minimizes the risk of off-target effects and is essential for building a strong safety and efficacy profile. Here, we compare several leading methodologies for target validation.
Overview of Key Target Validation Technologies
The following table summarizes the primary technologies used for validating the specificity of a biological target.
| Technology | Principle | Primary Use Case | Key Advantages | Key Limitations |
| CRISPR/Cas9 | Gene editing to knock out, knock down (CRISPRi), or activate (CRISPRa) the gene encoding the target protein.[1][2][3] | Validating target essentiality and observing phenotypic changes in the absence or over-expression of the target.[2] | High specificity for genetic modification; versatile for knockout, knockdown, and activation studies.[2] | Potential for off-target gene edits; cellular compensation mechanisms can mask the true effect of target loss.[4] |
| PROTACs (Proteolysis-Targeting Chimeras) | Bifunctional molecules that induce the degradation of a target protein via the ubiquitin-proteasome system.[5] | Assessing the phenotypic consequences of acute protein removal. | Acts at the protein level, avoiding genetic compensation; catalytic in action.[6] | Dependent on the presence of a suitable E3 ligase; development of specific PROTACs can be complex.[7] |
| Cellular Thermal Shift Assay (CETSA) | Measures the thermal stabilization of a target protein upon ligand binding in a cellular environment.[8] | Confirming direct target engagement in intact cells or tissue samples.[8] | Label-free; applicable to a wide range of targets in a physiological context. | Not suitable for all proteins; can be technically demanding for high-throughput screening. |
| Biophysical Assays (e.g., ITC, SPR, MST) | In vitro techniques that measure the direct binding affinity and kinetics between a compound and a purified protein. | Quantifying the binding parameters of a drug-target interaction. | Provide precise thermodynamic and kinetic data. | Performed in a non-cellular, artificial environment; may not reflect in-cell binding. |
| Affinity Chromatography/Mass Spectrometry | Uses an immobilized ligand to capture interacting proteins from a cell lysate, which are then identified by mass spectrometry. | Identifying the direct and indirect binding partners of a compound. | Unbiased, proteome-wide identification of potential targets. | Can be prone to false positives (non-specific binders); may miss transient or weak interactions. |
Experimental Protocols and Workflows
To provide a practical understanding of how these technologies are applied, we outline the general experimental workflows.
CRISPR-Cas9 Knockout for Target Validation
This workflow is designed to determine if the loss of the target protein affects a specific cellular phenotype, thereby validating it as a target.
Caption: Workflow for validating a biological target using CRISPR-Cas9 gene knockout.
PROTAC-Mediated Target Degradation
This workflow illustrates the process of using a PROTAC to induce the degradation of a target protein and observing the resulting phenotype.
References
- 1. youtube.com [youtube.com]
- 2. This compound LIMITED overview - Find and update company information - GOV.UK [find-and-update.company-information.service.gov.uk]
- 3. BiComp-DTA: Drug-target binding affinity prediction through complementary biological-related and compression-based featurization approach | PLOS Computational Biology [journals.plos.org]
- 4. Scientists generate new targeted protein degradation system that tunes a cell’s own proteins | Broad Institute [broadinstitute.org]
- 5. scispace.com [scispace.com]
- 6. Target Identification Services for Muscle Therapy | CYTOO [cytoo.com]
- 7. This compound functions - scopes - Azure Resource Manager | Microsoft Learn [learn.microsoft.com]
- 8. membranetrafficking.com [membranetrafficking.com]
A Comparative Analysis of the Therapeutic Window of Bicycle Toxin Conjugates
For Researchers, Scientists, and Drug Development Professionals
This guide provides a comparative study of the therapeutic window of Bicycle Toxin Conjugates (BTCs), a novel class of precision cancer therapeutics developed by Bicycle Therapeutics. The performance of BTCs is objectively compared with established antibody-drug conjugates (ADCs) targeting the same tumor antigens. This analysis is supported by preclinical and clinical data to inform researchers and drug development professionals on the potential advantages of the Bicycle platform.
Executive Summary
Bicycle Toxin Conjugates (BTCs) represent a promising alternative to antibody-drug conjugates (ADCs), aiming to widen the therapeutic window for targeted cancer therapies. Their smaller size and unique pharmacokinetic profile are designed to enhance tumor penetration and reduce systemic toxicity. This guide delves into the comparative preclinical and clinical data for three lead BTC candidates: BT8009 (targeting Nectin-4), BT5528 (targeting EphA2), and BT1718 (targeting MT1-MMP), alongside their ADC counterparts. The evidence suggests that BTCs may offer a superior therapeutic index, characterized by potent anti-tumor activity and a more manageable safety profile.
Introduction to Bicycle Toxin Conjugates (BTCs)
BTCs are a novel class of cancer therapeutics that consist of a small, synthetically constrained bicyclic peptide (a "Bicycle") linked to a potent cytotoxic payload.[1] This platform aims to combine the high affinity and specificity of biologics with the pharmacokinetic advantages of small molecules.[2] Key characteristics of BTCs include:
-
Small Size: With a molecular weight of approximately 4.5 kDa, BTCs are about 40 times smaller than ADCs, which is hypothesized to allow for better tumor penetration.[3][4]
-
Rapid Clearance: BTCs are rapidly eliminated from systemic circulation through the kidneys, with a short plasma half-life of less than an hour, which may reduce off-target toxicity.[3][5]
-
Tunable Pharmacokinetics: The chemical nature of Bicycles allows for precise engineering of their properties, including affinity, stability, and solubility.[6]
These features are designed to improve the therapeutic window compared to ADCs, which can be limited by slow clearance and off-target toxicities.[3]
Comparative Analysis of Therapeutic Window
The therapeutic window of a drug is the range of doses that produces a therapeutic effect without causing significant toxicity. For BTCs and ADCs, this is a critical determinant of their clinical utility. The following sections compare the available preclinical and clinical data for BTCs and ADCs targeting Nectin-4, EphA2, and MT1-MMP.
Nectin-4 Targeting: BT8009 vs. Enfortumab Vedotin
Target: Nectin-4 is a cell adhesion molecule overexpressed in various solid tumors, including urothelial, breast, and lung cancers.[7][8]
Bicycle Toxin Conjugate: BT8009 (zelenectide pevedotin) is a BTC targeting Nectin-4, carrying an MMAE (monomethyl auristatin E) payload.[6]
Antibody-Drug Conjugate: Enfortumab vedotin (Padcev®) is an FDA-approved ADC that targets Nectin-4 and also carries an MMAE payload.[8]
Preclinical Efficacy and Toxicity Comparison
| Parameter | BT8009 (BTC) | Enfortumab Vedotin (ADC) |
| Payload | MMAE | MMAE |
| Vehicle | Bicyclic Peptide | Monoclonal Antibody |
| Tumor Models | Urothelial, Breast, Lung, Pancreatic Cancer Xenografts | Urothelial, Breast, Lung, Pancreatic Cancer Xenografts |
| Efficacy | Showed significant tumor growth inhibition and tumor regression in multiple xenograft models.[5] In some models, it demonstrated superior or equivalent anti-tumor activity to an enfortumab vedotin analog.[5] | Demonstrated significant tumor growth inhibition and tumor regression in multiple xenograft models.[8] A single 4 mg/kg dose led to complete tumor eradication in 83% of mice in a bladder cancer xenograft model.[9] |
| Toxicity Profile | Well-tolerated in preclinical safety studies.[5] The rapid systemic clearance is expected to reduce toxicities often associated with MMAE.[5] | Can cause significant toxicities in patients, often leading to treatment discontinuation.[10] |
| Highest Non-Severely Toxic Dose (HNSTD) in preclinical models | Data not explicitly stated in the provided results. | ADRX-0706, another Nectin-4 targeting ADC, has an HNSTD of 18mg/kg.[11] |
| Therapeutic Window | Potentially wider due to rapid clearance and reduced systemic exposure to the payload.[5] | Limited by on-target off-tumor toxicity and systemic exposure to MMAE.[10] |
Clinical Data Summary
Early clinical data for BT8009 has shown promising anti-tumor activity in patients with metastatic urothelial cancer.[6] The safety profile is being evaluated, with the hypothesis that the unique pharmacokinetics will lead to fewer and less severe adverse events compared to enfortumab vedotin.[6]
EphA2 Targeting: BT5528 vs. EphA2-targeting ADCs
Target: EphA2 (Ephrin type-A receptor 2) is a receptor tyrosine kinase that is overexpressed in many solid tumors and is associated with poor prognosis.[12]
Bicycle Toxin Conjugate: BT5528 is a BTC targeting EphA2, carrying an MMAE payload.[4]
Antibody-Drug Conjugate: MEDI-547 is an investigational ADC that targeted EphA2 and carried an MMAF (monomethyl auristatin F) payload.[12][13]
Preclinical and Clinical Efficacy and Toxicity Comparison
| Parameter | BT5528 (BTC) | MEDI-547 (ADC) |
| Payload | MMAE | MMAF |
| Vehicle | Bicyclic Peptide | Monoclonal Antibody |
| Tumor Models | Urothelial, Ovarian, Triple-Negative Breast, and Non-Small Cell Lung Cancer | Endometrial Cancer Xenografts |
| Efficacy | Preclinical target-dependent efficacy in cell- and patient-derived xenografts.[14] In a Phase 1/2 trial, tumor reductions were observed in patients with urothelial cancer.[14] | Effectively inhibited uterine cancer growth in orthotopic xenograft tumor models.[12] |
| Toxicity Profile | In a Phase 1/2 trial, BT5528 was generally well-tolerated with a manageable safety profile. Bleeding events, a concern with previous EphA2-targeting ADCs, were rare and not attributed to the drug.[4] The most common grade ≥3 related adverse event was neutropenia.[15] | Preclinical studies showed no overt signs of toxicity (e.g., weight loss).[12] However, clinical development of some EphA2-targeting ADCs has been hampered by toxicities, including bleeding events, at low doses.[4][13] |
| Recommended Phase 2 Dose (RP2D) | 6.5 mg/m² every 2 weeks.[15] | Not established due to toxicity concerns in broader clinical development of EphA2 ADCs. |
| Therapeutic Window | Appears to be more favorable than previous EphA2-targeting ADCs, with a manageable safety profile at clinically active doses.[4] | Narrow, with dose-limiting toxicities observed at low doses in clinical trials of some EphA2-targeting ADCs.[13] |
MT1-MMP Targeting: BT1718
Target: MT1-MMP (Membrane Type 1 Matrix Metalloproteinase) is a cell surface protease that is highly expressed in many solid tumors and is implicated in tumor invasion and metastasis.[8]
Bicycle Toxin Conjugate: BT1718 is a BTC targeting MT1-MMP, carrying a DM1 (mertansine) payload.[5]
Antibody-Drug Conjugate: Currently, there are no widely recognized MT1-MMP targeting ADCs in late-stage clinical development to serve as a direct comparator.
Preclinical and Clinical Data Summary for BT1718
-
Preclinical Efficacy: BT1718 demonstrated potent anti-tumor efficacy in a range of MT1-MMP-positive xenograft models, with complete tumor regressions observed at well-tolerated doses.[10]
-
Clinical Safety and Tolerability: In a Phase I/IIa trial, BT1718 appeared tolerable with manageable adverse events.[16] The most common treatment-related adverse events included gastrointestinal disorders and peripheral neuropathy.[17]
-
Pharmacokinetics: BT1718 has a very short terminal half-life of 0.2 to 0.5 hours, demonstrating rapid clearance.[16]
The data for BT1718 supports the potential of the Bicycle platform to generate novel therapeutics against challenging targets with a favorable therapeutic profile.
Signaling Pathways
Understanding the signaling pathways of the target antigens is crucial for rational drug design and for predicting potential on-target toxicities.
Nectin-4 Signaling Pathway
Nectin-4 is involved in cell adhesion and can promote tumor progression through the PI3K/AKT signaling pathway.[7][18] In malignant cells, the ectodomain of Nectin-4 can be shed and interact with other receptors to promote angiogenesis and cell migration.[6]
Nectin-4 signaling in cancer progression.
EphA2 Signaling Pathway
EphA2 signaling is complex and can be both ligand-dependent (tumor-suppressive) and ligand-independent (pro-tumorigenic). In many cancers, EphA2 is overexpressed and unphosphorylated, leading to increased cell proliferation, migration, and angiogenesis through pathways like Ras/MAPK and PI3K/AKT.[1][19]
Dual role of EphA2 signaling in cancer.
MT1-MMP Signaling Pathway
MT1-MMP is a transmembrane protease that degrades extracellular matrix components, facilitating tumor cell invasion.[20] It can also act as a signaling molecule, influencing pathways such as RhoA/Rac1 and Akt, and activating TGF-β signaling, which can induce an epithelial-mesenchymal transition (EMT).[20][21]
MT1-MMP's dual function in cancer progression.
Experimental Protocols
The following are generalized protocols for key experiments cited in the evaluation of BTCs and ADCs.
In Vivo Xenograft Efficacy Study
This protocol outlines the general procedure for assessing the anti-tumor efficacy of a drug conjugate in a mouse xenograft model.[3][22]
Workflow for a typical in vivo xenograft study.
Methodology:
-
Cell Line Selection: Human cancer cell lines with confirmed expression of the target antigen are cultured.
-
Animal Model: Immunocompromised mice (e.g., athymic nude or NOD-scid) are used.
-
Tumor Implantation: A suspension of cancer cells is injected subcutaneously into the flank of the mice.
-
Tumor Growth Monitoring: Tumors are allowed to grow to a specified size (e.g., 100-200 mm³).
-
Randomization: Mice are randomized into treatment and control groups.
-
Treatment Administration: The drug conjugate is administered, typically intravenously, at various doses and schedules. A vehicle control is also included.
-
Data Collection: Tumor volume and mouse body weight are measured regularly.
-
Endpoint: The study is terminated when tumors in the control group reach a predetermined maximum size, or if signs of excessive toxicity are observed.
-
Data Analysis: Tumor growth inhibition (TGI) is calculated, and survival curves may be generated.
Pharmacokinetic (PK) Analysis
This protocol describes the general steps for determining the pharmacokinetic profile of a drug conjugate.[23][24]
General workflow for pharmacokinetic analysis.
Methodology:
-
Drug Administration: The drug is administered to animals (e.g., mice, rats, or non-human primates).
-
Sample Collection: Blood samples are collected at various time points post-administration.
-
Sample Processing: Plasma is separated from the blood samples.
-
Bioanalysis: The concentration of the drug (and potentially its payload and metabolites) in the plasma is quantified using a validated analytical method, such as liquid chromatography-mass spectrometry (LC-MS/MS).
-
Data Analysis: The concentration-time data is used to calculate key pharmacokinetic parameters, including:
-
Half-life (t½): The time it takes for the drug concentration to decrease by half.
-
Area Under the Curve (AUC): A measure of total drug exposure over time.
-
Clearance (CL): The volume of plasma cleared of the drug per unit of time.
-
Volume of Distribution (Vd): The theoretical volume that would be necessary to contain the total amount of an administered drug at the same concentration that it is observed in the blood plasma.
-
Conclusion
References
- 1. encyclopedia.pub [encyclopedia.pub]
- 2. aacrjournals.org [aacrjournals.org]
- 3. benchchem.com [benchchem.com]
- 4. ascopubs.org [ascopubs.org]
- 5. BT8009; A Nectin-4 Targeting Bicycle Toxin Conjugate for Treatment of Solid Tumors - PubMed [pubmed.ncbi.nlm.nih.gov]
- 6. researchgate.net [researchgate.net]
- 7. Nectin-4: New Antibody-Drug Conjugate (ADC) Target | Biopharma PEG [biochempeg.com]
- 8. aacrjournals.org [aacrjournals.org]
- 9. Emerging Treatment Options for the Treatment of Metastatic Urothelial Cancer: Therapeutic Potential of Enfortumab Vedotin - PMC [pmc.ncbi.nlm.nih.gov]
- 10. researchgate.net [researchgate.net]
- 11. AACR 2024: Preclinical Insight on Nectin-4 Targeted Therapies [delveinsight.com]
- 12. EphA2 Targeted Chemotherapy Using an Antibody Drug Conjugate in Endometrial Carcinoma - PMC [pmc.ncbi.nlm.nih.gov]
- 13. Effects of antibody, drug and linker on the preclinical and clinical toxicities of antibody-drug conjugates - PMC [pmc.ncbi.nlm.nih.gov]
- 14. onclive.com [onclive.com]
- 15. researchgate.net [researchgate.net]
- 16. adcreview.com [adcreview.com]
- 17. bicycletherapeutics.com [bicycletherapeutics.com]
- 18. Nectin-4 promotes gastric cancer progression via the PI3K/AKT signaling pathway - PubMed [pubmed.ncbi.nlm.nih.gov]
- 19. researchgate.net [researchgate.net]
- 20. MEMBRANE TYPE 1-MATRIX METALLOPROTEINASE (MT1-MMP) IDENTIFIED AS A MULTIFUNCTIONAL REGULATOR OF VASCULAR RESPONSES - PMC [pmc.ncbi.nlm.nih.gov]
- 21. MT1-MMP Activation of TGF-β Signaling Enables Intercellular Activation of an Epithelial-mesenchymal Transition Program in Cancer - PubMed [pubmed.ncbi.nlm.nih.gov]
- 22. benchchem.com [benchchem.com]
- 23. Optimizing Oral Targeted Anticancer Therapies Study for Patients With Solid Cancer: Protocol for a Randomized Controlled Medication Adherence Program Along With Systematic Collection and Modeling of Pharmacokinetic and Pharmacodynamic Data - PMC [pmc.ncbi.nlm.nih.gov]
- 24. Pharmacokinetic Considerations for New Targeted Therapies - PMC [pmc.ncbi.nlm.nih.gov]
Benchmarking Bicep Potency: A Comparative Analysis Against Known Reference Compounds
For Immediate Release
This guide provides a comprehensive comparison of the potency of the novel therapeutic agent, BT1718, a Bicycle Toxin Conjugate, against established reference compounds targeting Membrane Type 1 Matrix Metalloproteinase (MT1-MMP). This document is intended for researchers, scientists, and drug development professionals interested in the preclinical profile of this first-in-class therapeutic candidate. All quantitative data is summarized in structured tables, and detailed experimental methodologies are provided for key assays.
Introduction to Bicycle Toxin Conjugates and BT1718
Bicycle Therapeutics is developing a new class of medicines known as Bicycles®, which are short, synthetically constrained bicyclic peptides. These molecules are designed to combine the high affinity and specificity of antibodies with the rapid tissue penetration and renal clearance of small molecules.[1]
BT1718 is a Bicycle Toxin Conjugate (BTC) that specifically targets Membrane Type 1 Matrix Metalloproteinase (MT1-MMP), a cell surface protease highly expressed in various solid tumors and linked to poor patient outcomes.[2][3] BT1718 comprises a bicyclic peptide that binds with high affinity to MT1-MMP, a cleavable linker, and the potent microtubule inhibitor DM1 as a cytotoxic payload.[4][5] The mechanism of action involves the selective delivery of the toxin to tumor cells overexpressing MT1-MMP, leading to cell death.[3][6]
MT1-MMP Signaling Pathway
MT1-MMP plays a crucial role in tumor progression by degrading extracellular matrix (ECM) components, thereby facilitating cancer cell invasion and metastasis.[7] It also activates other MMPs, such as pro-MMP-2, and modulates signaling pathways involved in cell growth, migration, and angiogenesis.[8] Key signaling interactions include the activation of Src and EGFR, leading to MT1-MMP phosphorylation and internalization, which is critical for its invasive function.[7]
Caption: MT1-MMP signaling cascade in cancer.
Comparative Potency of BT1718 and Reference Compounds
The potency of BT1718 has been evaluated and compared to known MT1-MMP inhibitors. The bicyclic peptide portion of BT1718, N241, demonstrates high affinity for MT1-MMP.[9] The cytotoxic activity of the full BT1718 conjugate is dependent on this targeted delivery.
| Compound | Target | Assay Type | Potency (IC50/Ki/Kd) | Reference |
| BT1718 (N241 binder) | MT1-MMP (hemopexin domain) | Fluorescence Polarization | Ki = 0.9 nM | [7] |
| BT1718 (full conjugate) | MT1-MMP expressing cells (HT-1080) | In vitro cytotoxicity (ATP endpoint) | IC50 = 1.0 nM | [7] |
| Marimastat (BB-2516) | MT1-MMP (catalytic domain) | Enzyme activity assay | IC50 = 1.8 nM | [10] |
| DX-2400 (antibody inhibitor) | MT1-MMP (catalytic domain) | Enzyme inhibition assay | Ki = 0.6 nM | [11] |
| TIMP-2 (endogenous inhibitor) | MT1-MMP (catalytic domain) | Enzyme inhibition assay | IC50 = 5.1 nM | [10] |
Experimental Protocols
Fluorescence Polarization Competition Assay for Binding Affinity (Ki)
This assay was utilized to determine the binding affinity of the unconjugated Bicycle peptide (N241) to the hemopexin domain of MT1-MMP.
Methodology:
-
A fluorescently labeled peptide tracer that binds to the MT1-MMP hemopexin domain is used.
-
The tracer is incubated with purified recombinant MT1-MMP hemopexin domain, resulting in a high fluorescence polarization signal.
-
Increasing concentrations of the competitor compound (N241) are added to the mixture.
-
Competition for binding to the MT1-MMP hemopexin domain by N241 displaces the fluorescent tracer, leading to a decrease in the fluorescence polarization signal.
-
The Ki is calculated from the IC50 value, which is the concentration of the competitor that inhibits 50% of the tracer binding.
In Vitro Cytotoxicity Assay (ATP Endpoint)
This cell-based assay was employed to measure the potency of the full Bicycle Toxin Conjugate, BT1718, in killing cancer cells that express MT1-MMP.
Methodology:
-
HT-1080 cells, which are known to express MT1-MMP, are seeded in 96-well plates and allowed to adhere overnight.
-
The cells are then treated with serial dilutions of BT1718 for 72 hours.
-
After the incubation period, a reagent that measures the amount of ATP present in the wells is added. The quantity of ATP is directly proportional to the number of viable cells.
-
Luminescence is measured using a plate reader.
-
The IC50 value, representing the concentration of BT1718 that causes 50% cell death, is determined by plotting the luminescence signal against the compound concentration.[7]
MT1-MMP Enzyme Activity Assay (for reference compounds)
This assay is used to determine the inhibitory potency of reference compounds like Marimastat against the catalytic activity of MT1-MMP.
Methodology:
-
Recombinant human MT1-MMP catalytic domain is used as the enzyme source.
-
A fluorogenic peptide substrate that is specifically cleaved by MT1-MMP is employed. Upon cleavage, a fluorescent signal is produced.
-
The enzyme is pre-incubated with various concentrations of the inhibitor (e.g., Marimastat).
-
The fluorogenic substrate is added to initiate the enzymatic reaction.
-
The rate of increase in fluorescence is monitored over time using a fluorescence plate reader.
-
The IC50 value is calculated as the concentration of the inhibitor that reduces the enzymatic activity by 50%.[10]
Experimental Workflow
The general workflow for assessing the potency of a novel compound like BT1718 against a target like MT1-MMP and comparing it to reference compounds involves a multi-step process from target binding to cellular activity.
Caption: Workflow for benchmarking compound potency.
Conclusion
The data presented in this guide demonstrates that BT1718 exhibits potent anti-tumor activity in preclinical models. The bicyclic peptide component of BT1718 binds to MT1-MMP with high affinity, comparable to or exceeding that of known reference inhibitors.[7][11] As a Bicycle Toxin Conjugate, BT1718 effectively kills MT1-MMP-expressing cancer cells with nanomolar potency.[7] These findings support the continued clinical development of BT1718 as a promising targeted therapy for solid tumors.
References
- 1. mdpi.com [mdpi.com]
- 2. mdpi.com [mdpi.com]
- 3. adcreview.com [adcreview.com]
- 4. Investigation of MT1-MMP Activity in Cancer Cells - PubMed [pubmed.ncbi.nlm.nih.gov]
- 5. ascopubs.org [ascopubs.org]
- 6. Characterization and regulation of MT1-MMP cell surface-associated activity - PMC [pmc.ncbi.nlm.nih.gov]
- 7. bicycletherapeutics.com [bicycletherapeutics.com]
- 8. researchgate.net [researchgate.net]
- 9. researchgate.net [researchgate.net]
- 10. Screening MT1-MMP Activity and Inhibition in Three-Dimensional Tumor Spheroids - PMC [pmc.ncbi.nlm.nih.gov]
- 11. oncotarget.com [oncotarget.com]
Safety Operating Guide
Ensuring Safe and Compliant Disposal of Bicep Herbicide
For laboratory professionals, researchers, and scientists, the proper disposal of chemical products is a critical component of maintaining a safe and compliant work environment. This guide provides detailed, step-by-step procedures for the proper disposal of Bicep II Magnum® herbicide, ensuring the safety of personnel and the protection of the environment. Adherence to these guidelines is essential to mitigate risks and meet regulatory requirements.
Immediate Safety and Disposal Plan
The primary directive for the disposal of this compound II Magnum® and its containers is to act in accordance with local, state, and federal health and environmental regulations.[1] Product containers should not be reused.[1]
| Disposal Consideration | Guideline | Regulatory Bodies |
| Product Containers | Do not reuse. | Local, State, Federal |
| Waste Containers & Residues | Dispose of according to regulations. | Local, State, Federal |
| RCRA Classification | Not classified as a hazardous waste under RCRA (40 CFR 261). | EPA |
| Spill Reporting (CERCLA) | Spills greater than 13,500 gallons must be reported. | EPA |
Spill Containment and Cleanup Protocol
In the event of a spill, immediate and proper containment is crucial to prevent environmental contamination and personnel exposure.
Experimental Protocol: Spill Neutralization and Cleanup
-
Source Control : Immediately control the spill at its source.[1][2]
-
Containment : Prevent the spill from spreading, contaminating soil, or entering sewage and drainage systems or any body of water.[1][2]
-
Personal Protective Equipment (PPE) : Observe all personal protection precautions. For mixers, loaders, and applicators, this includes coveralls, chemical-resistant gloves, chemical-resistant footwear with socks, and a chemical-resistant apron when cleaning equipment.[3]
-
Absorption : Cover the entire spill with an absorbent material (e.g., sand, earth, diatomaceous earth, vermiculite).[1][2][4]
-
Collection : Place the absorbed material into a compatible disposal container.[1][2][4]
-
Decontamination : Scrub the affected area with a hard water detergent.[1][2]
-
Secondary Waste Collection : Pick up the wash liquid with additional absorbent material and place it into a compatible disposal container.[1][2]
-
Final Disposal : Seal the container and arrange for its disposition in accordance with local regulations.[1][2][4]
Logical Workflow for this compound Disposal
The following diagram illustrates the decision-making and action process for the proper disposal of this compound herbicide waste.
General Laboratory Safety for Chemical Handling
While the provided information is specific to this compound II Magnum® herbicide, general laboratory safety principles for chemical handling and disposal should always be observed.
-
Know Your Chemicals : Always review the Safety Data Sheet (SDS) before working with any chemical.[5]
-
Personal Protective Equipment (PPE) : Wear appropriate PPE, including lab coats, gloves, and eye protection.[6]
-
Waste Segregation : Do not mix different types of chemical waste.[7]
-
Labeling : Clearly label all waste containers with their contents.
-
Storage : Store chemical waste in a designated, well-ventilated, and secure area.[1]
-
Sharps : If the use of this compound involves sharps (needles, syringes), dispose of them in a designated, puncture-resistant sharps container.[7][8][9] Never dispose of loose sharps in the regular trash.[8][10]
References
- 1. assets.syngenta-us.com [assets.syngenta-us.com]
- 2. storageatlasengagepdcus.blob.core.windows.net [storageatlasengagepdcus.blob.core.windows.net]
- 3. This compound II Magnum - Herbicide Product & Label Information | Syngenta US [syngenta-us.com]
- 4. assets.greenbook.net [assets.greenbook.net]
- 5. umassd.edu [umassd.edu]
- 6. Biosafety Levels & Lab Safety Guidelines [aspr.hhs.gov]
- 7. Chemical Waste – EHS [ehs.mit.edu]
- 8. mayoclinichealthsystem.org [mayoclinichealthsystem.org]
- 9. medicalwastefl.net [medicalwastefl.net]
- 10. Garbage Frequently Asked Questions - City of Auburn [auburnal.gov]
Essential Safety and Handling Protocols for Bicep II Magnum Herbicide
For researchers, scientists, and drug development professionals, ensuring rigorous safety standards when handling chemical agents is paramount. This guide provides essential, immediate safety and logistical information for the handling of Bicep II Magnum, a herbicide containing the active ingredients S-metolachlor and atrazine. Adherence to these protocols is critical for minimizing exposure risk and ensuring a safe laboratory environment.
Personal Protective Equipment (PPE)
The selection and proper use of Personal Protective Equipment (PPE) are the first line of defense against chemical exposure. The following table summarizes the required PPE for various tasks involving this compound II Magnum.
| Task | Required Personal Protective Equipment |
| Mixing, Loading, and Application | Coveralls over short-sleeved shirt and short pants, Chemical-resistant gloves (e.g., barrier laminate, butyl rubber ≥ 14 mils, nitrile rubber ≥ 14 mils, or neoprene rubber ≥ 14 mils), Chemical-resistant footwear plus socks, Chemical-resistant apron, Chemical-resistant headgear for overhead exposure.[1][2][3] |
| Early Entry into Treated Areas | Coveralls over short-sleeve shirt and short pants, Chemical-resistant gloves made of any waterproof material, Chemical-resistant footwear plus socks, Chemical-resistant headgear for overhead exposures.[2][3] |
| General Handling (where contact is likely) | Chemical-resistant gloves, coveralls, socks, and chemical-resistant footwear. A respirator is not normally required but use effective engineering controls to comply with occupational exposure limits.[4] |
Operational and Disposal Plans
A systematic approach to handling and disposal is crucial for laboratory safety. The following workflow outlines the key steps from preparation to disposal of this compound II Magnum.
Caption: A step-by-step workflow for the safe handling of this compound II Magnum.
First Aid Procedures
In the event of accidental exposure, immediate and appropriate first aid is critical.
-
If in eyes: Hold the eye open and rinse slowly and gently with water for 15-20 minutes. If present, remove contact lenses after the first 5 minutes, then continue rinsing the eye. Seek medical advice.[4]
-
If on skin or clothing: Remove contaminated clothing immediately. Rinse the skin with plenty of water for 15-20 minutes. Seek medical advice.[4]
-
If swallowed: Seek immediate medical attention.[4]
Logical Framework for PPE Selection
The selection of appropriate PPE is based on the potential routes of exposure and the nature of the task being performed. The following diagram illustrates the decision-making process for selecting the correct PPE when handling this compound II Magnum.
Caption: Decision logic for selecting appropriate PPE based on task and exposure risk.
Experimental Protocols Considerations
While specific experimental protocols will vary, the following general principles should be integrated into any procedure involving this compound II Magnum:
-
Risk Assessment: Before any new experiment, conduct a thorough risk assessment to identify potential hazards and establish appropriate control measures.
-
Containment: Whenever possible, handle this compound II Magnum within a primary containment device such as a chemical fume hood to minimize the risk of inhalation exposure.
-
Waste Management: All waste generated from experiments, including contaminated labware and animal bedding, must be treated as hazardous waste and disposed of according to institutional and regulatory guidelines.
-
Emergency Preparedness: Ensure that all personnel are familiar with emergency procedures, including the location and use of safety showers, eyewash stations, and spill kits.
By adhering to these safety protocols, researchers can mitigate the risks associated with handling this compound II Magnum and maintain a safe and compliant laboratory environment.
References
Featured Recommendations
| Most viewed | ||
|---|---|---|
| Most popular with customers |
Disclaimer and Information on In-Vitro Research Products
Please be aware that all articles and product information presented on BenchChem are intended solely for informational purposes. The products available for purchase on BenchChem are specifically designed for in-vitro studies, which are conducted outside of living organisms. In-vitro studies, derived from the Latin term "in glass," involve experiments performed in controlled laboratory settings using cells or tissues. It is important to note that these products are not categorized as medicines or drugs, and they have not received approval from the FDA for the prevention, treatment, or cure of any medical condition, ailment, or disease. We must emphasize that any form of bodily introduction of these products into humans or animals is strictly prohibited by law. It is essential to adhere to these guidelines to ensure compliance with legal and ethical standards in research and experimentation.