molecular formula C25H21NO6S B13436914 ST362

ST362

Katalognummer: B13436914
Molekulargewicht: 463.5 g/mol
InChI-Schlüssel: GJUAGRMNTHWYBB-MHWRWJLKSA-N
Achtung: Nur für Forschungszwecke. Nicht für den menschlichen oder tierärztlichen Gebrauch.
Usually In Stock
  • Klicken Sie auf QUICK INQUIRY, um ein Angebot von unserem Expertenteam zu erhalten.
  • Mit qualitativ hochwertigen Produkten zu einem WETTBEWERBSFÄHIGEN Preis können Sie sich mehr auf Ihre Forschung konzentrieren.

Beschreibung

ST362 is a useful research compound. Its molecular formula is C25H21NO6S and its molecular weight is 463.5 g/mol. The purity is usually 95%.
BenchChem offers high-quality this compound suitable for many research applications. Different packaging options are available to accommodate customers' requirements. Please inquire for more information about this compound including the price, delivery time, and more detailed information at info@benchchem.com.

Eigenschaften

Molekularformel

 C25H21NO6S

Molekulargewicht

 463.5 g/mol

IUPAC-Name

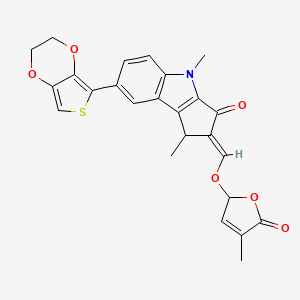
 (2E)-7-(2,3-dihydrothieno[3,4-b][1,4]dioxin-5-yl)-1,4-dimethyl-2-[(4-methyl-5-oxo-2H-furan-2-yl)oxymethylidene]-1H-cyclopenta[b]indol-3-one

InChI

 InChI=1S/C25H21NO6S/c1-12-8-19(32-25(12)28)31-10-16-13(2)20-15-9-14(4-5-17(15)26(3)21(20)22(16)27)24-23-18(11-33-24)29-6-7-30-23/h4-5,8-11,13,19H,6-7H2,1-3H3/b16-10+

InChI-Schlüssel

 GJUAGRMNTHWYBB-MHWRWJLKSA-N

Isomerische SMILES

 CC1/C(=C\OC2C=C(C(=O)O2)C)/C(=O)C3=C1C4=C(N3C)C=CC(=C4)C5=C6C(=CS5)OCCO6

Kanonische SMILES

 CC1C(=COC2C=C(C(=O)O2)C)C(=O)C3=C1C4=C(N3C)C=CC(=C4)C5=C6C(=CS5)OCCO6

Herkunft des Produkts

 United States

Foundational & Exploratory

Core Assumptions of Linear Regression: A Technical Guide for Researchers

Author: BenchChem Technical Support Team. Date: December 2025

The Four Principal Assumptions

For the results of a linear regression model to be considered valid for inference and prediction, four principal assumptions concerning the model's residuals (the differences between observed and predicted values) must be met.[7][8] These are often remembered by the acronym LINE : L inearity, I ndependence, N ormality, and E qual variance.

  • Linearity : The most fundamental assumption is that a linear relationship exists between the independent and dependent variables.[1][9] This means that a change in an independent variable is associated with a proportional change in the dependent variable.[1]

  • Independence : The errors (or residuals) of the model are assumed to be independent of each other.[1][10] This implies that the residual for one observation does not predict the residual for another.[10] This is particularly important for time-series data where consecutive observations may be correlated (a condition known as autocorrelation).[3][11]

  • Normality : The residuals of the model are assumed to be normally distributed.[12][13] This assumption is crucial for the validity of hypothesis tests, p-values, and the construction of confidence intervals.[1][14]

  • Homoscedasticity (Equal Variance) : The variance of the residuals should be constant across all levels of the independent variables.[1][3][15] The opposite condition, where the variance of the residuals changes, is called heteroscedasticity.[15]

Additionally, for multiple linear regression, two other assumptions are critical:

  • No Multicollinearity : The independent variables should not be highly correlated with each other.[13][16] High multicollinearity can make it difficult to determine the individual effect of each predictor on the outcome variable.[6][12]

  • No Endogeneity : The independent variables should not be correlated with the error term.[9] Violation of this, often due to an omitted variable, can cause biased and inconsistent parameter estimates.[9][17]

Logical Relationship of Core Assumptions

The following diagram illustrates how these core assumptions underpin a valid Ordinary Least Squares (OLS) regression model, which is the most common method for estimating the parameters of a linear regression.

G cluster_assumptions Core Assumptions cluster_model Model Validity linearity Linearity model Valid OLS Regression Model linearity->model Ensures unbiased coefficients independence Independence of Errors independence->model Ensures correct standard errors normality Normality of Errors normality->model Validates hypothesis tests homoscedasticity Homoscedasticity homoscedasticity->model Ensures efficient coefficients

Caption: Core assumptions for a valid OLS regression model.

Methodologies for Verifying Assumptions

A systematic workflow is essential to validate these assumptions. This typically involves a combination of visual inspection of plots and formal statistical tests.

Experimental Protocol: A Step-by-Step Validation Workflow

  • Initial Data Exploration :

    • Action : Create scatter plots of the dependent variable against each independent variable.

    • Purpose : To visually assess the Linearity assumption. The points should appear to follow a straight line.[1][16]

  • Model Fitting :

    • Action : Fit the linear regression model to the data using a statistical software package (e.g., R, Python, SPSS).

    • Purpose : To obtain the predicted values and, most importantly, the residuals, which are the basis for testing the remaining assumptions.

  • Residual Analysis :

    • Action 1 (Homoscedasticity & Linearity) : Plot the residuals against the predicted (fitted) values.

      • Purpose : This is a key diagnostic plot. For the Homoscedasticity assumption to hold, the residuals should be randomly scattered around the zero line without any discernible pattern (like a cone or fan shape, which indicates heteroscedasticity).[12][15][18] This plot can also reveal non-linearity if the residuals show a curved pattern.[7]

    • Action 2 (Normality) : Create a Quantile-Quantile (Q-Q) plot of the residuals or a histogram.[14][16]

      • Purpose : For the Normality assumption, the points on the Q-Q plot should fall closely along the diagonal line.[12] A histogram of residuals should resemble a bell curve.[14]

    • Action 3 (Independence) : For time-series data, plot the residuals against the observation order.

      • Purpose : To check for Autocorrelation . There should be no clear pattern; the residuals should appear random.

  • Formal Statistical Testing :

    • Action : Conduct formal statistical tests to complement the visual diagnostics.

    • Purpose : To obtain quantitative evidence for or against the assumptions. (See table below for specific tests).

Diagnostic Workflow Diagram

The diagram below outlines the logical flow for testing the assumptions of a linear regression model after it has been fitted.

G cluster_tests Assumption Diagnostics cluster_checks Check For... start Fit Linear Regression Model get_residuals Calculate Residuals (Observed - Predicted) start->get_residuals p1 Plot Residuals vs. Predicted Values get_residuals->p1 p2 Create Q-Q Plot of Residuals get_residuals->p2 p3 Perform Statistical Tests get_residuals->p3 check1 Random Scatter? (Homoscedasticity) p1->check1 check2 Points on Line? (Normality) p2->check2 check3 P-values > α? (Formal Tests) p3->check3 end_node Assumptions Met: Proceed with Inference check1->end_node check2->end_node check3->end_node

Caption: Workflow for residual analysis in linear regression.

Summary of Assumptions, Diagnostics, and Implications

The following table summarizes each core assumption, provides common diagnostic methods, and outlines the consequences of violation, which is critical for researchers in fields like drug development where model accuracy is paramount.

AssumptionDescriptionDiagnostic Methods (Visual & Formal)Consequences of Violation
Linearity The relationship between independent (X) and dependent (Y) variables is linear.[1][16]Visual : Scatter plot of Y vs. X shows a linear pattern.[16] Residuals vs. Predicted plot shows no curved pattern.[7]Biased and inaccurate coefficient estimates. The model systematically over or under-predicts, rendering it unreliable.[4]
Independence of Errors The residuals are independent and not correlated with each other.[1][10]Visual : Residuals vs. Time/Order plot shows no pattern. Formal : Durbin-Watson test (p-value > 0.05 indicates no autocorrelation).[10][19]Standard errors of the coefficients become incorrect, leading to unreliable hypothesis tests and confidence intervals.[10][20]
Normality of Errors The residuals follow a normal distribution.[13][16]Visual : Histogram of residuals is bell-shaped. Q-Q plot of residuals follows the diagonal line.[12][16] Formal : Shapiro-Wilk test or Kolmogorov-Smirnov test (p-value > 0.05 supports normality).[16][21][22]Invalidates p-values and confidence intervals, making statistical inference unreliable, especially with small sample sizes.[6][14]
Homoscedasticity The variance of the residuals is constant across all levels of the predictors.[3][15]Visual : Residuals vs. Predicted plot shows a random scatter with constant vertical spread (no "cone" shape).[15][18] Formal : Breusch-Pagan test or White test (p-value > 0.05 supports homoscedasticity).[16][23]Standard errors are biased, making hypothesis tests untrustworthy. The model's efficiency is reduced.[20]
No Multicollinearity Independent variables are not highly correlated with each other.[13][16]Formal : Variance Inflation Factor (VIF). (VIF > 10 is often considered problematic).[16] Correlation matrix (coefficients should be < 0.8).[16]Inflates the variance of coefficient estimates, making them unstable and difficult to interpret. Weakens the statistical power of the model.[12][17]

In clinical research and drug development, the rigorous validation of these assumptions is not merely a statistical formality; it is a prerequisite for generating reliable evidence, making sound decisions, and ensuring the integrity of scientific findings.[24] Failure to do so can have significant consequences, impacting everything from preclinical analysis to the interpretation of clinical trial results.

References

Unlocking Insights: A Technical Guide to Regression Analysis in Biomedical Research

Author: BenchChem Technical Support Team. Date: December 2025

For Immediate Release

[City, State] – December 4, 2025 – In the intricate landscape of biomedical research and drug development, the ability to discern meaningful relationships from complex datasets is paramount. Regression analysis stands as a cornerstone statistical methodology, enabling researchers to model, predict, and understand the interplay between variables. This in-depth technical guide provides a comprehensive overview of regression analysis, tailored for researchers, scientists, and drug development professionals. From fundamental concepts to practical applications, this whitepaper serves as a vital resource for harnessing the power of regression to drive scientific discovery.

Introduction to Regression Analysis in a Biomedical Context

Regression analysis is a powerful statistical tool used to examine the relationship between a dependent variable (the outcome of interest) and one or more independent variables (predictors or explanatory variables).[1] In biomedical research, this technique is indispensable for a myriad of applications, from identifying risk factors for a disease to evaluating the efficacy of a new therapeutic intervention.[2] The core idea is to understand how the outcome variable changes as the predictor variables change, allowing for both the quantification of relationships and the prediction of future outcomes.[2]

Regression models are instrumental in advancing medical knowledge by translating raw data into actionable insights.[3] They are employed in all phases of clinical trials and preclinical studies to analyze and interpret results, ensuring the validity and reproducibility of research findings.[3][4]

Core Types of Regression Analysis in Biomedical Research

The choice of regression model is dictated by the nature of the dependent variable.[5] Understanding the different types of regression is crucial for selecting the appropriate analytical approach.

Regression Type Dependent Variable Type Common Biomedical Applications
Linear Regression Continuous (e.g., blood pressure, tumor volume)Assessing the relationship between a biomarker and a physiological measurement; dose-response analysis.[2]
Multiple Linear Regression ContinuousModeling the effect of multiple factors (e.g., age, weight, dosage) on a continuous outcome.[2]
Logistic Regression Binary (e.g., disease presence/absence, patient survival)Identifying risk factors for a disease; predicting the likelihood of treatment success.[6]
Cox Proportional Hazards Regression Time-to-event (e.g., time to disease recurrence, time to death)Analyzing survival data in clinical trials to compare the efficacy of different treatments.
Poisson Regression Count (e.g., number of lesions, number of adverse events)Modeling the frequency of events, such as the number of asthma attacks in a given period.

Methodologies for Key Experiments

The successful application of regression analysis hinges on a well-designed experimental protocol and a robust statistical analysis plan.

Experimental Protocol: Preclinical Dose-Response Study

This protocol outlines a typical preclinical study to assess the dose-dependent efficacy of a novel anti-cancer compound (Compound X) on tumor growth in a mouse xenograft model.

  • Objective: To determine the relationship between the dose of Compound X and the reduction in tumor volume.

  • Animal Model: Immunocompromised mice (e.g., NOD/SCID) will be used.

  • Procedure:

    • Human cancer cells will be implanted subcutaneously into the flank of each mouse.

    • Once tumors reach a palpable size (e.g., 100-150 mm³), mice will be randomized into treatment and control groups (n=10 mice per group).

    • Treatment groups will receive varying doses of Compound X (e.g., 1 mg/kg, 5 mg/kg, 10 mg/kg, 25 mg/kg) administered daily via intraperitoneal injection.

    • The control group will receive a vehicle control.

    • Tumor volume will be measured every three days for a period of 21 days using calipers (Volume = 0.5 * length * width²).

  • Statistical Analysis:

    • The primary endpoint will be the tumor volume at day 21.

    • A simple linear regression model will be used to assess the relationship between the dose of Compound X (independent variable) and the final tumor volume (dependent variable).

    • The assumptions of the linear regression model (linearity, independence of errors, homoscedasticity, and normality of residuals) will be checked.

    • The regression equation and the coefficient of determination (R²) will be reported.

Methodology: Building and Validating a Regression Model

A systematic approach to model building is essential for generating reliable and interpretable results.

  • Data Preparation and Exploration:

    • Clean the dataset to handle missing values and outliers.

    • Visualize the data using scatter plots to explore the relationships between variables.

    • Transform variables if necessary (e.g., log transformation) to meet model assumptions.

  • Model Specification and Fitting:

    • Choose the appropriate regression model based on the research question and the nature of the dependent variable.

    • Specify the independent variables to be included in the model based on prior knowledge and exploratory data analysis.

    • Fit the model to the data using statistical software (e.g., R, SAS, SPSS).

  • Checking Model Assumptions:

    • For linear regression, check for linearity, independence of errors, homoscedasticity (constant variance of residuals), and normality of residuals.[3][7][8]

    • Residual plots are a key tool for diagnosing violations of these assumptions.[8]

  • Model Interpretation and Reporting:

    • Interpret the regression coefficients to understand the magnitude and direction of the relationship between each predictor and the outcome.

    • Report the p-values to assess the statistical significance of each predictor.

    • For logistic regression, report the odds ratios and their 95% confidence intervals.

    • Present the overall model fit using metrics like R-squared for linear regression.

Data Presentation

Clear and concise presentation of regression analysis results is crucial for effective communication of research findings. Quantitative data should be summarized in well-structured tables.

Table 1: Multiple Linear Regression Analysis of Factors Associated with Systolic Blood Pressure

Variable Coefficient (β) Standard Error t-statistic p-value
(Intercept)80.505.2015.48<0.001
Age (years)0.650.106.50<0.001
BMI ( kg/m ²)1.200.254.80<0.001
Daily Sodium Intake (g)2.500.505.00<0.001
Model Summary
R-squared0.72
Adjusted R-squared0.70
F-statistic35.6<0.001
N150

Table 2: Logistic Regression Analysis of Risk Factors for Disease X

Variable Odds Ratio (OR) 95% Confidence Interval p-value
Age (per year)1.051.02 - 1.080.002
Smoking Status (Smoker vs. Non-smoker)2.501.50 - 4.17<0.001
Presence of Biomarker Y (Positive vs. Negative)3.201.80 - 5.71<0.001
Model Summary
N500

Mandatory Visualizations

Visual representations of workflows and pathways can greatly enhance the understanding of complex analytical processes and biological systems.

regression_workflow A 1. Formulate Research Question B 2. Design Experiment & Collect Data A->B C 3. Data Cleaning & Preprocessing B->C D 4. Exploratory Data Analysis C->D E 5. Choose Regression Model D->E F 6. Build & Fit the Model E->F G 7. Check Model Assumptions F->G G->F Refine Model H 8. Interpret & Report Results G->H I 9. Validate Model H->I

A high-level workflow for a regression analysis project.

model_selection Start What is the nature of the dependent variable? Continuous Continuous Start->Continuous Binary Binary Start->Binary TimeToEvent Time-to-Event Start->TimeToEvent Count Count Start->Count Linear Linear Regression Continuous->Linear Logistic Logistic Regression Binary->Logistic Cox Cox Regression TimeToEvent->Cox Poisson Poisson Regression Count->Poisson signaling_pathway Regression can model how Growth Factor Concentration and Drug Dose predict the level of Cell Proliferation. cluster_input Inputs (Predictors) cluster_pathway Signaling Pathway cluster_output Output (Dependent Variable) GrowthFactor Growth Factor Concentration Receptor Receptor Activation GrowthFactor->Receptor DrugDose Drug Dose (Inhibitor) PI3K PI3K DrugDose->PI3K Receptor->PI3K AKT AKT Phosphorylation PI3K->AKT CellProliferation Cell Proliferation (Response) AKT->CellProliferation

References

The Cornerstone of Discovery: A Technical Guide to Independent and Dependent Variables in Research

Author: BenchChem Technical Support Team. Date: December 2025

An in-depth exploration for researchers, scientists, and drug development professionals on the fundamental principles of experimental design, data interpretation, and the critical interplay of variables in scientific inquiry.

Defining the Core Concepts: Independent and Dependent Variables

At its most fundamental level, an experiment is a structured procedure designed to test a hypothesis. This is achieved by manipulating one variable to observe its effect on another.[1][2][3]

  • Independent Variable (IV): This is the variable that the researcher intentionally manipulates or changes.[1][2][3][4] It is the presumed "cause" in a cause-and-effect relationship.[1][2] In drug development, the independent variable is often the dosage of a new medication, the frequency of its administration, or the type of therapeutic intervention.[5][6]

  • Dependent Variable (DV): This is the variable that is measured or observed to see how it is affected by the changes in the independent variable.[1][2][3] It represents the "effect" or outcome of the experiment.[1][2] In a clinical trial, dependent variables could include changes in blood pressure, tumor size, or the concentration of a specific biomarker in the blood.[5]

The relationship between these two types of variables is the central focus of most quantitative research. The goal is to determine if a change in the independent variable leads to a predictable and significant change in the dependent variable.[7][8]

A Case Study in Drug Development: The Antihypertensive Drug Trial

To illustrate the practical application of these concepts, let's consider a hypothetical Phase II clinical trial for a new antihypertensive drug, "Hypotensaril."

Research Hypothesis: Administration of Hypotensaril will lead to a dose-dependent reduction in systolic blood pressure in patients with grade 1 hypertension.

In this scenario:

  • Independent Variable: The daily dosage of Hypotensaril administered to the participants. This is manipulated by the researchers, with different groups of patients receiving different doses.

  • Dependent Variable: The change in systolic blood pressure (SBP) from the baseline measurement. This is the outcome that is measured to assess the drug's efficacy.

Data Presentation: Summarized Results of the Hypotensaril Phase II Trial

The following tables summarize the quantitative data from this hypothetical trial, demonstrating the relationship between the independent and dependent variables.

Table 1: Baseline Characteristics of Study Participants

CharacteristicPlacebo (n=50)Hypotensaril 25 mg (n=50)Hypotensaril 50 mg (n=50)Hypotensaril 100 mg (n=50)
Age (years), mean ± SD 55.2 ± 8.154.9 ± 7.855.5 ± 8.355.1 ± 7.9
Sex (Male/Female) 27/2326/2428/2227/23
Baseline Systolic BP (mmHg), mean ± SD 145.3 ± 4.2145.8 ± 4.5145.1 ± 4.1145.6 ± 4.3
Baseline Diastolic BP (mmHg), mean ± SD 92.1 ± 3.192.5 ± 3.391.9 ± 3.092.3 ± 3.2

Table 2: Change in Systolic Blood Pressure (SBP) after 12 Weeks of Treatment

Treatment GroupMean Change in SBP from Baseline (mmHg)Standard Deviation of Changep-value vs. Placebo
Placebo -2.53.1-
Hypotensaril 25 mg -8.74.2<0.01
Hypotensaril 50 mg -15.44.8<0.001
Hypotensaril 100 mg -19.25.1<0.001

The data clearly indicates a dose-dependent effect of Hypotensaril on systolic blood pressure. As the dosage (independent variable) increases, the reduction in SBP (dependent variable) becomes more pronounced.

Experimental Protocols: Ensuring Rigor and Reproducibility

The validity of the relationship between independent and dependent variables hinges on the quality of the experimental design and protocol. A well-defined protocol minimizes bias and ensures that the observed effects can be confidently attributed to the manipulation of the independent variable.

Detailed Methodology for the Hypotensaril Clinical Trial

3.1. Study Design: A 12-week, multi-center, randomized, double-blind, placebo-controlled Phase II clinical trial.

3.2. Participant Selection:

  • Inclusion Criteria:

    • Male and female participants aged 18-70 years.

    • Diagnosed with grade 1 hypertension (Systolic BP 140-159 mmHg or Diastolic BP 90-99 mmHg) according to the latest clinical guidelines.[9]

    • Willing and able to provide informed consent.

  • Exclusion Criteria:

    • Secondary hypertension.

    • History of significant cardiovascular events (e.g., myocardial infarction, stroke) within the past 6 months.

    • Severe renal or hepatic impairment.

    • Use of other antihypertensive medications that cannot be safely discontinued.

3.3. Randomization and Blinding:

  • Participants are randomly assigned in a 1:1:1:1 ratio to one of the four treatment arms (Placebo, 25 mg, 50 mg, or 100 mg Hypotensaril).

  • Randomization is stratified by study center to ensure a balanced distribution.

  • Both participants and investigators are blinded to the treatment allocation.

3.4. Intervention:

  • The investigational drug (Hypotensaril or matching placebo) is administered orally once daily.

  • Participants are instructed to take the medication at the same time each day.

3.5. Measurement of the Dependent Variable (Blood Pressure):

  • Blood pressure is measured at baseline and at weeks 4, 8, and 12.

  • Measurements are taken using a validated automated oscillometric device.[10]

  • To ensure accuracy, the following standardized procedure is followed:

    • Participants rest in a quiet room for at least 5 minutes before measurement.[11]

    • Measurements are taken in the seated position with the back supported and feet flat on the floor.[11]

    • The arm is supported at the level of the heart.[10]

    • Three readings are taken at 1-minute intervals, and the average of the last two readings is recorded.[3]

  • 24-hour ambulatory blood pressure monitoring (ABPM) is performed at baseline and at week 12 to assess the drug's effect over a full day.[3][12]

3.6. Statistical Analysis:

  • The primary endpoint is the change in mean sitting systolic blood pressure from baseline to week 12.

  • An Analysis of Covariance (ANCOVA) model is used to compare the mean change in SBP between each Hypotensaril dose group and the placebo group, with baseline SBP as a covariate.

Visualizing the Relationships: Diagrams and Pathways

Visual representations are powerful tools for understanding the logical flow of an experiment and the biological mechanisms at play.

Experimental Workflow

The following diagram illustrates the workflow of the Hypotensaril clinical trial, from patient recruitment to data analysis.

experimental_workflow cluster_screening Screening & Recruitment cluster_randomization Randomization & Blinding cluster_intervention Intervention (12 Weeks) cluster_data_collection Data Collection cluster_analysis Data Analysis p1 Patient Population with Grade 1 Hypertension p2 Inclusion/Exclusion Criteria Assessment p1->p2 p3 Informed Consent p2->p3 r1 Randomization (1:1:1:1) p3->r1 i1 Placebo r1->i1 i2 Hypotensaril 25 mg r1->i2 i3 Hypotensaril 50 mg r1->i3 i4 Hypotensaril 100 mg r1->i4 d2 Follow-up BP Measurements (Weeks 4, 8, 12) i1->d2 i2->d2 i3->d2 i4->d2 d1 Baseline BP Measurement d1->r1 a1 Statistical Analysis (ANCOVA) d2->a1 d3 24-hr Ambulatory BP Monitoring d3->a1 a2 Efficacy & Safety Evaluation a1->a2

Workflow of the Hypotensaril clinical trial.
Logical Relationship of Variables

This diagram illustrates the fundamental cause-and-effect relationship being tested in the experiment.

variable_relationship IV Independent Variable (Hypotensaril Dosage) DV Dependent Variable (Change in Systolic Blood Pressure) IV->DV Influences CV Controlled Variables (Age, Diet, Activity Level, etc.) CV->DV Held constant to isolate the effect of the IV ConfV Potential Confounding Variables (e.g., Adherence to Medication) ConfV->DV

Logical relationship between variables in the study.
Signaling Pathway: Mechanism of Action of Beta-Blockers

To provide a more in-depth biological context, the following diagram illustrates the signaling pathway of beta-blockers, a common class of antihypertensive drugs. This demonstrates how understanding the underlying mechanism is crucial in drug development. Beta-blockers work by blocking the effects of catecholamines like epinephrine (B1671497) and norepinephrine (B1679862) on beta-adrenergic receptors.[7] This leads to a decrease in heart rate and blood pressure.[7][8]

beta_blocker_pathway cluster_cell Cardiac Myocyte beta_receptor Beta-1 Adrenergic Receptor g_protein Gs Protein beta_receptor->g_protein Activates adenylyl_cyclase Adenylyl Cyclase g_protein->adenylyl_cyclase Activates camp cAMP adenylyl_cyclase->camp Converts ATP to pka Protein Kinase A camp->pka Activates calcium_channel L-type Calcium Channel pka->calcium_channel Phosphorylates effect Decreased Heart Rate & Reduced Blood Pressure calcium_channel->effect Increased Ca2+ influx leads to increased heart rate catecholamines Catecholamines (Epinephrine, Norepinephrine) catecholamines->beta_receptor Activates beta_blocker Beta-Blocker (e.g., Hypotensaril) beta_blocker->beta_receptor Blocks beta_blocker->effect Inhibits this pathway, leading to

Simplified signaling pathway of beta-blockers.

Conclusion

The meticulous identification, manipulation, and measurement of independent and dependent variables are the cornerstones of robust scientific research. As demonstrated through the hypothetical "Hypotensaril" clinical trial, a clear understanding of these variables, coupled with rigorous experimental protocols and data analysis, is essential for advancing our knowledge and developing new therapeutic interventions. For researchers, scientists, and drug development professionals, a mastery of these fundamental principles is not merely academic—it is the very essence of their contribution to science and medicine.

References

Unveiling Relationships: A Technical Guide to Simple Linear Regression for Experimental Data

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

In the realm of experimental science and drug development, understanding the relationship between two continuous variables is a frequent necessity. Simple linear regression is a powerful statistical method that provides a framework to model and quantify these relationships. This in-depth technical guide delves into the core concepts of simple linear regression, offering practical insights into its application for analyzing experimental data. We will explore the underlying principles, essential assumptions, and the interpretation of model outputs, all illustrated with relevant examples from laboratory settings.

Core Concepts of Simple Linear Regression

Simple linear regression is a statistical method used to model the relationship between a single independent variable (predictor or explanatory variable, denoted as x) and a single dependent variable (response or outcome variable, denoted as y).[1] The relationship is modeled using a straight line.[1]

The Linear Regression Model

The fundamental equation of a simple linear regression model is:

y = β₀ + β₁x + ε

Where:

  • y is the dependent variable.[1]

  • x is the independent variable.[1]

  • β₀ is the y-intercept of the regression line, representing the predicted value of y when x is 0.[1]

  • β₁ is the slope of the regression line, indicating the change in y for a one-unit change in x.[1]

  • ε is the error term, which accounts for the variability in y that cannot be explained by the linear relationship with x.[2]

The goal of simple linear regression is to find the best-fit line that minimizes the error between the observed data points and the line itself.

Assumptions of Simple Linear Regression

For the results of a simple linear regression to be valid, several assumptions about the data must be met:

  • Linearity: The relationship between the independent and dependent variables must be linear.[1][3][4] This can be visually assessed with a scatter plot.

  • Independence of Errors: The errors (residuals) should be independent of each other.[3][4] This means there should be no correlation between consecutive residuals.

  • Homoscedasticity (Constant Variance): The variance of the errors should be constant across all levels of the independent variable.[1][3][4] A plot of residuals against predicted values can help check this assumption.

  • Normality of Errors: The errors should be normally distributed.[1][4] This can be checked using a histogram of the residuals or a Q-Q plot.

The logical flow of performing a simple linear regression analysis is depicted in the following diagram.

linear_regression_workflow cluster_start Start cluster_data Data Collection & Preparation cluster_model Model Fitting & Evaluation cluster_end Conclusion Start Define Research Question (Relationship between two continuous variables) CollectData Collect Experimental Data (Paired observations of x and y) Start->CollectData CheckAssumptions Check Assumptions (Linearity, Independence, Homoscedasticity, Normality) CollectData->CheckAssumptions FitModel Fit Simple Linear Regression Model (Estimate β₀ and β₁ using Least Squares) CheckAssumptions->FitModel EvaluateModel Evaluate Model Fit (R-squared, p-value, Residual Analysis) FitModel->EvaluateModel Interpret Interpret Results (Slope, Intercept, Significance) EvaluateModel->Interpret Is model a good fit? Report Report Findings (Tables, Figures, Narrative) Interpret->Report

Figure 1: Workflow of a Simple Linear Regression Analysis.

Parameter Estimation: The Method of Least Squares

The most common method for estimating the parameters (β₀ and β₁) of a linear regression model is the method of least squares .[5][6] This method aims to find the line that minimizes the sum of the squared differences between the observed values of the dependent variable (y) and the values predicted by the regression line (ŷ).[5][7] These differences are known as residuals.

The formulas for calculating the slope (β₁) and the y-intercept (β₀) using the least squares method are derived from minimizing the sum of squared residuals. For a set of n data points (xᵢ, yᵢ):

Slope (β₁):

β₁ = Σ((xᵢ - x̄)(yᵢ - ȳ)) / Σ((xᵢ - x̄)²)

Y-intercept (β₀):

β₀ = ȳ - β₁x̄

Where:

  • xᵢ and yᵢ are the individual data points.

  • x̄ and ȳ are the means of the independent and dependent variables, respectively.

The logical relationship for calculating the least squares estimates is as follows:

least_squares Data Paired Experimental Data (x₁, y₁), (x₂, y₂), ..., (xₙ, yₙ) Means Calculate Means (x̄ and ȳ) Data->Means Deviations Calculate Deviations (xᵢ - x̄) and (yᵢ - ȳ) Means->Deviations Intercept Calculate Y-Intercept (β₀) Means->Intercept Products Calculate Sum of Products Σ((xᵢ - x̄)(yᵢ - ȳ)) Deviations->Products SumSqX Calculate Sum of Squares for x Σ((xᵢ - x̄)²) Deviations->SumSqX Slope Calculate Slope (β₁) Products->Slope SumSqX->Slope Slope->Intercept

Figure 2: Calculation of Least Squares Estimates.

Model Evaluation

Once the regression model is fitted, it is crucial to evaluate how well it represents the data. Several metrics are used for this purpose.

MetricDescriptionInterpretation
R-squared (R²) Also known as the coefficient of determination, it represents the proportion of the variance in the dependent variable that is predictable from the independent variable.[8]Values range from 0 to 1. A higher R² indicates a better fit of the model to the data. For example, an R² of 0.85 means that 85% of the variation in the dependent variable can be explained by the independent variable.[8]
Adjusted R-squared A modified version of R-squared that adjusts for the number of predictors in a model.It is more suitable for comparing models with different numbers of independent variables.
p-value The p-value for the slope coefficient (β₁) tests the null hypothesis that there is no linear relationship between the independent and dependent variables.A small p-value (typically < 0.05) indicates that you can reject the null hypothesis and conclude that there is a statistically significant linear relationship between the variables.
Residual Plots A graphical tool used to assess the assumptions of the linear regression model.Patterns in the residual plot can indicate violations of assumptions like non-linearity or heteroscedasticity. Ideally, the residuals should be randomly scattered around zero.[8]

Application in Experimental Data Analysis

Simple linear regression is widely used in various experimental contexts within drug development and scientific research. Below are detailed examples of its application.

Experiment 1: Protein Quantification using the Bradford Assay

Objective: To determine the concentration of an unknown protein sample by creating a standard curve using a series of known protein concentrations.

Experimental Protocol:

  • Preparation of Standards: A series of bovine serum albumin (BSA) standards with known concentrations (e.g., 0, 0.1, 0.2, 0.4, 0.6, 0.8, 1.0 mg/mL) are prepared by diluting a stock solution.[3]

  • Sample Preparation: The unknown protein sample is diluted to fall within the linear range of the assay.[3]

  • Assay Procedure:

    • Aliquots of each standard and the diluted unknown sample are added to separate test tubes or microplate wells.[9]

    • Bradford reagent is added to each tube/well and mixed.[9]

    • After a short incubation period (e.g., 5 minutes), the absorbance of each sample is measured at 595 nm using a spectrophotometer.[3]

Data Presentation:

BSA Concentration (mg/mL) (x)Absorbance at 595 nm (y)
0.00.050
0.10.152
0.20.251
0.40.448
0.60.653
0.80.851
1.01.049

Regression Analysis:

A simple linear regression is performed with BSA concentration as the independent variable (x) and absorbance as the dependent variable (y).

ParameterEstimateStandard Errort-valuep-value
Intercept (β₀)0.0510.0086.375<0.001
Slope (β₁)0.9980.01566.533<0.001
R-squared: 0.9989

The resulting regression equation is: Absorbance = 0.051 + 0.998 * (BSA Concentration) .

To determine the concentration of the unknown protein sample, its absorbance is measured and the concentration is calculated using the regression equation. For example, if the unknown sample has an absorbance of 0.550, its concentration would be calculated as: (0.550 - 0.051) / 0.998 ≈ 0.500 mg/mL.

The workflow for creating a standard curve using linear regression is illustrated below.

standard_curve_workflow PrepareStandards Prepare Standards (Known Concentrations) MeasureResponse Measure Instrument Response (e.g., Absorbance) PrepareStandards->MeasureResponse PlotData Plot Response vs. Concentration (Scatter Plot) MeasureResponse->PlotData LinearRegression Perform Linear Regression (y = β₀ + β₁x) PlotData->LinearRegression Equation Obtain Standard Curve Equation and R-squared value LinearRegression->Equation Calculate Calculate Concentration of Unknown using the equation Equation->Calculate Unknown Measure Response of Unknown Sample Unknown->Calculate

References

A-Z of Regression Analysis in Psychology Research: A Technical Guide

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

This guide provides a comprehensive overview of regression analysis, a powerful statistical tool used in psychological research to model and understand the relationships between variables.[1][2][3] It is designed to equip researchers with the knowledge to appropriately apply regression techniques to answer complex research questions.

Core Principle: When to Employ Regression Analysis

At its core, regression analysis is used for two primary purposes: prediction and explanation .[3][4] It is the appropriate method when a researcher seeks to understand how one or more independent variables (IVs), or predictors, relate to a single dependent variable (DV), or outcome.[1][3]

Use regression analysis to answer questions such as:

  • Prediction/Forecasting: Can we predict a future or current outcome based on a set of known factors? For example, can college GPA be predicted from high school SAT scores and hours of study per week?[1][3]

  • Etiology and Explanation: What are the key factors that contribute to a particular psychological phenomenon? For instance, what is the relationship between levels of perceived stress, social support, and the severity of depressive symptoms?[3]

  • Controlling for Variables: How does a primary relationship of interest hold up after accounting for the influence of other, potentially confounding, variables? A researcher might want to examine the effect of a new therapeutic intervention on anxiety levels while statistically controlling for the patient's age and initial symptom severity.[2][5]

  • Theory Testing: Does a theoretical model hold true? Regression is essential for testing complex psychological theories, such as models of mediation and moderation, which examine the how and when of an effect.[6][7][8]

Common Regression Models in Psychological Science

The choice of regression model depends on the nature of the research question and the type of variables being studied.[9][10][11][12]

Model Type Description Typical Research Question Variable Types
Simple Linear Regression Models the linear relationship between a single IV and a single DV.[9][10][11]How does the number of hours slept predict next-day mood rating?IV: ContinuousDV: Continuous
Multiple Linear Regression Extends simple regression by including two or more IVs to predict a single DV.[1][9] This allows for the assessment of the unique contribution of each predictor.[13]How do IQ, motivation, and socioeconomic status collectively predict academic achievement?IVs: Continuous or CategoricalDV: Continuous
Logistic Regression Used when the dependent variable is dichotomous (i.e., has only two possible outcomes).[9][14][15] It models the probability of an outcome occurring.[9][16]What is the likelihood of a patient responding to a specific treatment (yes/no) based on their demographic and clinical characteristics?IVs: Continuous or CategoricalDV: Dichotomous (e.g., 0/1, Pass/Fail)
Hierarchical Regression The researcher, based on theory, dictates the order in which predictor variables are entered into the model in a series of steps or "blocks".[5][17] This method is used to determine if newly added variables provide a significant improvement in prediction over the variables already in the model.[5][18][19]After controlling for demographic factors like age and gender, does a measure of psychological resilience still significantly predict levels of burnout in healthcare workers?IVs: Continuous or CategoricalDV: Continuous or Dichotomous
Mediation & Moderation Analysis These are advanced applications of regression used to test theoretical pathways.[7][20] Mediation explains how or why an IV affects a DV through an intermediary variable (the mediator).[8][20] Moderation identifies when or for whom an IV affects a DV, by examining how a third variable (the moderator) changes the strength or direction of the primary relationship.[8][21]Mediation: Does a new mindfulness intervention (IV) reduce stress (DV) by increasing self-awareness (mediator)?Moderation: Is the relationship between stress (IV) and depression (DV) stronger for individuals with low social support (moderator)?IVs: Continuous or CategoricalDV: Continuous or Dichotomous

The Foundational Assumptions of Linear Regression

  • Linearity: The relationship between the independent variable(s) and the dependent variable is assumed to be linear.[22][24][25][26] This means a straight line should best describe the relationship between the variables.

  • Independence of Errors: The residuals (the differences between the observed and predicted values) are independent of one another.[23][24][25] This is particularly important in data with a time-series component.

  • Homoscedasticity: The variance of the residuals is constant at every level of the independent variable(s).[23][24][25][26] In other words, the spread of the residuals should be roughly the same across the entire range of predicted values.

  • Normality of Errors: The residuals of the model are assumed to be normally distributed.[22][23][25][26] It is a common misconception that the variables themselves must be normally distributed; only the errors of the model need to follow a normal distribution.[22][23]

  • No Multicollinearity: In multiple regression, the independent variables should not be too highly correlated with each other.[25][26] High multicollinearity can make it difficult to determine the unique contribution of each predictor.

G cluster_workflow Workflow for Choosing a Regression Model Start Define Research Question and Variables Q_DV_Type What is the nature of the Dependent Variable (DV)? Start->Q_DV_Type Continuous Continuous Q_DV_Type->Continuous Continuous Categorical Categorical (Dichotomous) Q_DV_Type->Categorical Dichotomous Q_IV_Count How many Independent Variables (IVs)? Continuous->Q_IV_Count Logistic Use Logistic Regression Categorical->Logistic One_IV One IV Q_IV_Count->One_IV One Multiple_IVs Two or More IVs Q_IV_Count->Multiple_IVs Multiple Simple_Linear Use Simple Linear Regression One_IV->Simple_Linear Q_Theory Is there a theoretical reason to order the entry of IVs or test complex pathways? Multiple_IVs->Q_Theory Multiple_Linear Use Multiple Linear Regression Q_Theory->Multiple_Linear No (Simultaneous Entry) Hierarchical Use Hierarchical Regression Q_Theory->Hierarchical Yes (Control/Order) Med_Mod Use Mediation/ Moderation Analysis Q_Theory->Med_Mod Yes (How/When)

Decision tree for selecting the appropriate regression model.

Example Experimental Protocol

Research Question: To what extent do prior academic achievement (high school GPA) and study habits (average weekly study hours) predict final exam scores in an undergraduate psychology course, after controlling for a student's pre-existing anxiety levels?

Methodology:

  • Participants: 250 undergraduate students enrolled in an introductory psychology course at a large university.

  • Materials:

    • Demographic Questionnaire: Collects basic information and self-reported high school GPA.

    • Study Habits Log: Participants log their average weekly hours spent studying for the course over the semester.

    • Generalized Anxiety Disorder 7-item (GAD-7) Scale: A validated self-report measure to assess baseline anxiety symptoms at the beginning of the semester.

    • Final Exam: A standardized, 100-point final examination for the course.

  • Procedure:

    • At the beginning of the semester, students complete the demographic questionnaire and the GAD-7 scale.

    • Throughout the semester, students are prompted weekly to log their study hours.

    • At the end of the semester, final exam scores are collected from the course instructor.

  • Proposed Analysis: Hierarchical Multiple Regression

    • Model 1: The control variable, GAD-7 score, is entered into the regression model to predict the final exam score.

    • Model 2: High school GPA and average weekly study hours are added to the model.

    • The analysis will determine if the addition of the academic variables in Model 2 significantly improves the prediction of the final exam score, over and above the variance explained by anxiety alone.[5]

Data Presentation: Interpreting Regression Output

The output of a regression analysis is typically summarized in a table. The following is a hypothetical result from the experiment described above.

Table 1: Hierarchical Regression Predicting Final Exam Score

Model Variable B SE β t p-value
1 (Constant) 85.12 2.45 34.74 < .001
GAD-7 Score -0.75 0.25 -0.19 -3.00 .003
Model 1 Summary F(1, 248) = 9.00, p = .003, R² = .035
2 (Constant) 40.30 4.88 8.26 < .001
GAD-7 Score -0.41 0.20 -0.10 -2.05 .041
High School GPA 8.55 1.50 0.32 5.70 < .001
Weekly Study Hours 1.20 0.30 0.23 4.00 < .001
Model 2 Summary F(3, 246) = 25.67, p < .001, R² = .238

| Model 2 Change Statistics | | | | | ΔF(2, 246) = 31.25, p < .001, ΔR² = .203 | |

  • B (Unstandardized Coefficient): The change in the DV for a one-unit change in the IV. For every one-hour increase in weekly study, the exam score is predicted to increase by 1.20 points, holding other variables constant.

  • β (Standardized Coefficient): Standardized coefficients allow for comparison of the relative strength of the predictors. Here, High School GPA (β = 0.32) is the strongest predictor.

  • p-value: Indicates statistical significance (typically < .05). All predictors in Model 2 are significant.

  • R² (R-squared): The proportion of variance in the DV that is explained by the IVs in the model. Model 1 (anxiety) explains 3.5% of the variance in exam scores. Model 2 explains 23.8%.

  • ΔR² (R-squared Change): The change in R-squared between models. The addition of GPA and study hours explained an additional 20.3% of the variance in exam scores, a significant improvement.[5]

Visualizing Complex Relationships

Graphviz diagrams can illustrate the theoretical pathways tested with regression.

G cluster_mediation Mediation Pathway X Intervention (X) M Self-Awareness (M) (Mediator) X->M a Y Stress Reduction (Y) X->Y c' (Direct Effect) M->Y b

A simple mediation model (X → M → Y).

G cluster_moderation Moderation Relationship X Stress (X) Y Depression (Y) X->Y Main Effect Interaction X * Z X->Interaction Z Social Support (Z) (Moderator) Z->Y Z->Interaction Interaction->Y Interaction Effect

A simple moderation model (Z moderates X → Y).

Conclusion

Regression analysis is a versatile and indispensable tool in psychology research, enabling scientists to move beyond simple descriptions of data to build and test predictive and explanatory models.[1][2] A thorough understanding of its different forms, underlying assumptions, and proper application is critical for producing robust and meaningful scientific insights. When used correctly, regression provides a powerful framework for dissecting the complex interplay of variables that define human behavior and psychological processes.

References

Foundational Principles of Multiple Regression Analysis: An In-depth Technical Guide for Researchers and Drug Development Professionals

Author: BenchChem Technical Support Team. Date: December 2025

An in-depth technical guide on the core principles of multiple regression analysis, tailored for researchers, scientists, and professionals in drug development. This guide delves into the fundamental assumptions, methodological workflow, and interpretation of multiple regression, providing a robust framework for its application in scientific research.

Introduction to Multiple Regression Analysis

Multiple regression analysis is a powerful statistical technique used to understand the relationship between a single dependent variable and two or more independent variables.[1][2] In the context of drug development and clinical research, it is an indispensable tool for identifying factors that may influence a particular outcome, such as treatment efficacy or patient response.[3] For instance, researchers might use multiple regression to determine how factors like drug dosage, patient age, and biomarker levels collectively predict a change in a clinical endpoint.[1] It is important to remember that regression analysis reveals relationships between variables but does not inherently imply causation.[1]

Core Principles and Assumptions

Key Assumptions of Multiple Regression:

  • Linearity: The relationship between each independent variable and the dependent variable is assumed to be linear. This can be visually inspected using scatterplots of each predictor against the outcome.[2]

  • Independence of Errors: The errors (the differences between the observed and predicted values) are assumed to be independent of one another. This assumption is particularly important in studies with repeated measures or clustered data.

  • Homoscedasticity: The variance of the errors is constant across all levels of the independent variables. A plot of residuals against predicted values should show no discernible pattern, such as a funnel shape.

  • Normality of Errors: The errors are assumed to be normally distributed. This can be checked by examining a histogram or a Q-Q plot of the residuals.

  • No Multicollinearity: The independent variables should not be too highly correlated with each other. High correlation, known as multicollinearity, can make it difficult to determine the individual effect of each predictor. This can be assessed using metrics like the Variance Inflation Factor (VIF).[4]

Methodological Workflow for Multiple Regression Analysis

A systematic approach to multiple regression analysis ensures robustness and reproducibility. The following diagram outlines a typical workflow for conducting such an analysis in a research setting.

workflow A 1. Define Research Question and Hypotheses B 2. Data Collection and Preparation A->B C 3. Exploratory Data Analysis B->C D 4. Model Building C->D E 5. Model Diagnostics (Assumption Checking) D->E E->D If assumptions violated, re-specify model F 6. Interpretation of Results E->F If assumptions met G 7. Reporting and Visualization F->G

A typical workflow for multiple regression analysis.

Experimental Protocol: A Hypothetical Case Study in Drug Efficacy

To illustrate the application of multiple regression in drug development, we present a detailed protocol for a hypothetical clinical study.

Study Title: A Phase II, Randomized, Double-Blind, Placebo-Controlled Study to Evaluate the Efficacy of "LogiStat" in Reducing LDL Cholesterol in Patients with Hypercholesterolemia.

Objective: To determine the relationship between the dosage of LogiStat, patient age, and baseline LDL cholesterol levels on the percentage reduction in LDL cholesterol after 12 weeks of treatment.

Methodology:

  • Participant Recruitment: A total of 150 participants diagnosed with hypercholesterolemia, aged between 40 and 70 years, were recruited for the study. Participants were randomized into three arms: Placebo, LogiStat 10mg, and LogiStat 20mg.

  • Data Collection:

    • Dependent Variable: Percentage change in LDL cholesterol from baseline to week 12.

    • Independent Variables:

      • Drug Dosage (0mg for Placebo, 10mg, 20mg)

      • Patient Age (in years)

      • Baseline LDL Cholesterol (in mg/dL)

  • Statistical Analysis Plan:

    • A multiple linear regression model will be fitted to the data.

    • Model Equation: LDL_Reduction (%) = β₀ + β₁(Dosage) + β₂(Age) + β₃(Baseline_LDL) + ε

    • Assumption Checks: All core assumptions of multiple regression (linearity, independence, homoscedasticity, normality of errors, and no multicollinearity) will be formally tested.

    • Model Evaluation: The overall significance of the model will be assessed using the F-statistic. The proportion of variance in LDL reduction explained by the model will be determined by the R-squared value.

    • Interpretation of Coefficients: The regression coefficients (β) for each independent variable will be interpreted to understand their individual contribution to the change in LDL cholesterol, while holding other variables constant. A p-value of < 0.05 will be considered statistically significant.

Data Presentation: Summarized Results of the Hypothetical Study

The following table summarizes the results of the multiple regression analysis from our hypothetical study on "LogiStat".

VariableUnstandardized Coefficient (B)Standard ErrorStandardized Coefficient (β)t-statisticp-value
(Intercept)5.252.102.500.013
Drug Dosage (mg)1.500.250.606.00<0.001
Age (years)-0.150.05-0.18-3.000.003
Baseline LDL (mg/dL)0.100.040.152.500.014

Model Summary:

  • R-squared (R²): 0.72

  • Adjusted R-squared: 0.71

  • F-statistic: 118.5

  • p-value (F-statistic): <0.001

Interpretation of Results

The results from the multiple regression analysis indicate that the overall model is statistically significant (F = 118.5, p < 0.001), explaining approximately 71% of the variance in LDL cholesterol reduction (Adjusted R² = 0.71).

  • Drug Dosage: For each 1mg increase in the dosage of LogiStat, the percentage reduction in LDL cholesterol is expected to increase by 1.50%, holding age and baseline LDL constant. This effect is statistically significant (p < 0.001).

  • Age: For each one-year increase in age, the percentage reduction in LDL cholesterol is expected to decrease by 0.15%, holding dosage and baseline LDL constant. This effect is statistically significant (p = 0.003).

  • Baseline LDL: For each 1 mg/dL increase in baseline LDL cholesterol, the percentage reduction in LDL cholesterol is expected to increase by 0.10%, holding dosage and age constant. This effect is statistically significant (p = 0.014).

Visualization of Logical Relationships

The following diagram illustrates the logical relationship between the independent and dependent variables in our hypothetical multiple regression model.

logical_relationship cluster_iv Independent Variables cluster_dv Dependent Variable IV1 Drug Dosage DV LDL Cholesterol Reduction (%) IV1->DV IV2 Patient Age IV2->DV IV3 Baseline LDL IV3->DV

Predictors of LDL Cholesterol Reduction.

Conclusion

Multiple regression analysis is a versatile and powerful tool for researchers and professionals in drug development. By understanding its foundational principles, adhering to a systematic workflow, and carefully interpreting the results, it is possible to gain significant insights into the complex interplay of factors that influence clinical outcomes. This guide provides a foundational understanding to aid in the robust application of this essential statistical method.

References

Interpreting the Y-Intercept and Slope in Linear Regression: A Technical Guide for Researchers

Author: BenchChem Technical Support Team. Date: December 2025

An in-depth guide for researchers, scientists, and drug development professionals on the core principles of linear regression analysis, focusing on the practical interpretation of the y-intercept and slope. This document provides detailed experimental protocols, quantitative data summaries, and visual workflows to facilitate a deeper understanding of this fundamental statistical method.

Introduction to Linear Regression in Scientific Research

Linear regression is a powerful statistical tool used to model the relationship between a dependent variable and one or more independent variables.[1] In the context of life sciences and drug development, it is frequently employed to analyze experimental data, identify trends, and make predictions.[1] This guide will delve into the two key components of a simple linear regression equation—the y-intercept and the slope—providing a foundational understanding for their correct interpretation in various research applications.

The fundamental linear regression equation is expressed as:

Y = β₀ + β₁X + ε

Where:

  • Y is the dependent (response) variable.

  • X is the independent (predictor) variable.

  • β₀ is the y-intercept.

  • β₁ is the slope.

  • ε is the error term, representing the variability in Y that cannot be explained by X.

Core Concepts: The Y-Intercept (β₀) and the Slope (β₁)

Interpreting the Y-Intercept (β₀)

The y-intercept is the predicted value of the dependent variable (Y) when the independent variable (X) is equal to zero.[2][3][4] While mathematically straightforward, its practical interpretation depends heavily on the context of the experiment.

  • Meaningful Interpretation: In some scenarios, a value of zero for the independent variable is experimentally valid and meaningful. For example, in a dose-response study, a zero dose represents a control condition (no drug administered). In this case, the y-intercept would represent the baseline response of the biological system in the absence of the treatment.[5]

  • Meaningless Interpretation (Extrapolation): In many experiments, an X value of zero may be outside the range of the collected data or physically impossible. For instance, in a study relating drug concentration to absorbance, a zero concentration should theoretically yield zero absorbance. However, the regression line might intersect the y-axis at a non-zero value due to background noise or other experimental factors. Extrapolating the interpretation of the y-intercept in such cases can be misleading.[6] It is crucial to only apply the interpretation of the y-intercept within the range of the observed data.[6]

Interpreting the Slope (β₁)

The slope represents the change in the dependent variable (Y) for a one-unit change in the independent variable (X).[2][6][7] The sign of the slope (positive or negative) indicates the direction of the relationship.

  • Positive Slope: A positive slope signifies a direct relationship, where an increase in the independent variable leads to a predicted increase in the dependent variable.

  • Negative Slope: A negative slope indicates an inverse relationship, where an increase in the independent variable leads to a predicted decrease in the dependent variable.

The magnitude of the slope quantifies the steepness of the line and the strength of the linear relationship.[7] A larger absolute value of the slope suggests a more substantial change in Y for each unit change in X.

Practical Applications and Experimental Protocols

To illustrate the interpretation of the y-intercept and slope, we will explore two common applications in drug development and research: the Bradford protein assay and a dose-response analysis for IC₅₀ determination.

Example 1: Protein Quantification using the Bradford Assay

The Bradford assay is a widely used colorimetric method to determine the total protein concentration in a sample.[2] The assay relies on the binding of Coomassie Brilliant Blue G-250 dye to proteins, which results in a color change that can be measured by a spectrophotometer at 595 nm. A standard curve is generated using a series of known protein concentrations (e.g., Bovine Serum Albumin - BSA) and their corresponding absorbance readings. This standard curve is then used to determine the concentration of an unknown protein sample.

  • Preparation of Reagents:

    • Prepare a 1 mg/mL stock solution of Bovine Serum Albumin (BSA).

    • Prepare a series of BSA standards with concentrations ranging from 0.1 to 1.0 mg/mL by diluting the stock solution.

    • Prepare the Bradford reagent (commercially available or prepared in the lab).

  • Assay Procedure:

    • Pipette 20 µL of each BSA standard, the unknown protein sample, and a blank (buffer with no protein) into separate cuvettes or wells of a microplate.

    • Add 1 mL of Bradford reagent to each cuvette/well and mix thoroughly.

    • Incubate at room temperature for 5 minutes.

    • Measure the absorbance of each sample at 595 nm using a spectrophotometer.

  • Data Analysis:

    • Subtract the absorbance of the blank from the absorbance readings of all standards and the unknown sample.

    • Plot the corrected absorbance values (Y-axis) against the known BSA concentrations (X-axis).

    • Perform a linear regression analysis on the standard curve data to obtain the equation of the line (Y = β₁X + β₀).

BSA Concentration (mg/mL) (X)Absorbance at 595 nm (Y)
0.00.050
0.10.150
0.20.255
0.40.460
0.60.655
0.80.860
1.01.050

Linear Regression Equation: Absorbance = 1.005 * [BSA] + 0.052

  • Slope (β₁ = 1.005): For every 1 mg/mL increase in BSA concentration, the absorbance at 595 nm is predicted to increase by 1.005 units. This indicates a strong positive linear relationship between protein concentration and absorbance within this range.

  • Y-Intercept (β₀ = 0.052): The y-intercept of 0.052 represents the predicted absorbance when the BSA concentration is zero. This small positive value is likely due to background absorbance from the reagent and the cuvette and is not practically interpreted as a true protein concentration.

Bradford_Assay_Workflow cluster_prep Preparation cluster_assay Assay cluster_analysis Data Analysis BSA_Standards Prepare BSA Standards (0.1-1.0 mg/mL) Mix Mix Samples with Bradford Reagent BSA_Standards->Mix Unknown_Sample Prepare Unknown Protein Sample Unknown_Sample->Mix Bradford_Reagent Prepare Bradford Reagent Bradford_Reagent->Mix Incubate Incubate at Room Temperature (5 min) Mix->Incubate Measure_Abs Measure Absorbance at 595 nm Incubate->Measure_Abs Standard_Curve Plot Standard Curve (Abs vs. Concentration) Measure_Abs->Standard_Curve Lin_Reg Perform Linear Regression Y = β₁X + β₀ Standard_Curve->Lin_Reg Calc_Conc Calculate Unknown Concentration Lin_Reg->Calc_Conc

Caption: Logical flow for estimating IC₅₀ using linear regression on dose-response data.

Quantitative Structure-Activity Relationship (QSAR) Modeling

Quantitative Structure-Activity Relationship (QSAR) is a computational modeling method used in drug discovery to predict the biological activity of chemical compounds based on their physicochemical properties. [3]Linear regression is a fundamental technique used in developing QSAR models.

In QSAR, the biological activity (e.g., pIC₅₀) is the dependent variable (Y), and various molecular descriptors (e.g., molecular weight, logP, polar surface area) are the independent variables (X). A multiple linear regression model can be built to establish a mathematical relationship between the descriptors and the activity.

  • Data Collection: Compile a dataset of chemical structures and their corresponding experimentally determined biological activities.

  • Descriptor Calculation: Calculate a wide range of molecular descriptors for each compound in the dataset.

  • Data Splitting: Divide the dataset into a training set (for model building) and a test set (for model validation).

  • Model Building: Use multiple linear regression to build a model that relates the selected descriptors to the biological activity for the training set.

  • Model Validation: Evaluate the predictive performance of the model on the test set.

QSAR_Workflow QSAR Model Development Workflow Data_Collection Data Collection (Structures & Activities) Descriptor_Calc Descriptor Calculation Data_Collection->Descriptor_Calc Data_Split Data Splitting (Training & Test Sets) Descriptor_Calc->Data_Split Model_Building Model Building (Multiple Linear Regression) Data_Split->Model_Building Model_Validation Model Validation Model_Building->Model_Validation New_Compound_Prediction Prediction for New Compounds Model_Validation->New_Compound_Prediction

Caption: A simplified workflow for developing a QSAR model using linear regression.

Conclusion

References

Exploring different types of regression models for scientific data.

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

In the realm of scientific discovery and drug development, the ability to model and interpret complex data is paramount. Regression analysis serves as a powerful statistical toolkit for understanding the relationships between variables, predicting outcomes, and ultimately driving informed decisions. This in-depth technical guide explores a range of regression models, from foundational linear approaches to more sophisticated nonlinear and machine learning techniques, providing a roadmap for their application to scientific data.

Fundamental Regression Models

Linear Regression: Unveiling Linear Relationships

Linear regression is a foundational statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data.[1][2] It is often the first step in data analysis to understand trends and make predictions when a linear relationship is suspected.[1]

Experimental Protocol: Correlating Drug Concentration with Efficacy

A common application of linear regression in pre-clinical research is to assess the relationship between the concentration of a drug and its measured efficacy in an in-vitro assay.

  • Cell Culture and Treatment: A specific cell line relevant to the disease of interest is cultured under standard conditions. The cells are then treated with a range of concentrations of the investigational drug.

  • Efficacy Measurement: After a predetermined incubation period, a biochemical assay is performed to measure a specific biological response indicative of the drug's efficacy. This could be, for example, the inhibition of a particular enzyme or the reduction in cell viability.

  • Data Collection: The drug concentration (independent variable) and the corresponding efficacy measurement (dependent variable) are recorded for each treatment condition.

  • Regression Analysis: Simple linear regression is applied to the collected data to model the relationship between drug concentration and efficacy. The output of the analysis includes the regression equation (Y = bX + A), where Y is the predicted efficacy, X is the drug concentration, b is the slope of the line, and A is the y-intercept.[2] The coefficient of determination (R-squared) is also calculated to assess the goodness of fit of the model.

Table 1: Linear Regression Analysis of Drug Concentration and Efficacy

Drug Concentration (nM)Measured Efficacy (% Inhibition)Predicted Efficacy (% Inhibition)
15.25.5
210.810.3
524.524.5
1048.748.5
2095.396.5

Logical Relationship: Linear Regression Workflow

linear_regression_workflow Data Experimental Data (Concentration vs. Efficacy) Model Linear Regression Model (Y = bX + A) Data->Model Output Model Output (Slope, Intercept, R-squared) Model->Output Interpretation Interpretation (Assess Linearity and Strength of Relationship) Output->Interpretation

Caption: Workflow for applying linear regression to experimental data.

Polynomial Regression: Modeling Non-Linear Trends

When the relationship between variables is not a straight line, polynomial regression can be employed to fit a curvilinear relationship.[3][4] This method extends linear regression by adding polynomial terms (e.g., squared, cubed) of the independent variable to the model, allowing it to capture more complex patterns in the data.[5][6]

Experimental Protocol: Optimizing Fertilizer Concentration for Crop Yield

In agricultural science, polynomial regression is often used to model the non-linear relationship between fertilizer concentration and crop yield, where increasing fertilizer initially boosts yield, but excessive amounts can become detrimental.[7][8]

  • Experimental Plot Setup: A field is divided into multiple plots, and a specific crop is planted under uniform conditions.

  • Fertilizer Application: Different concentrations of a fertilizer are applied to the plots, with each concentration level replicated across multiple plots to ensure statistical robustness.

  • Crop Growth and Harvest: The crops are allowed to grow to maturity under controlled environmental conditions. At the end of the growing season, the yield from each plot is harvested and measured.

  • Data Collection: The fertilizer concentration (independent variable) and the corresponding crop yield (dependent variable) are recorded for each plot.

  • Regression Analysis: A polynomial regression model is fitted to the data. The degree of the polynomial (e.g., quadratic, cubic) is chosen based on the observed trend in the data and statistical measures of model fit.[9] The resulting equation describes the curved relationship between fertilizer and yield, allowing for the determination of the optimal fertilizer concentration for maximum yield.[7]

Table 2: Polynomial Regression Analysis of Fertilizer Concentration and Crop Yield

Fertilizer Concentration ( kg/ha )Observed Crop Yield (tons/ha)Predicted Crop Yield (tons/ha)
01.51.6
503.23.1
1004.54.6
1504.84.7
2004.14.2

Logical Relationship: Polynomial Regression Workflow

polynomial_regression_workflow Data Experimental Data (Fertilizer vs. Yield) Model Polynomial Regression Model (Y = b2X^2 + b1X + A) Data->Model Output Model Output (Coefficients, R-squared) Model->Output Interpretation Interpretation (Identify Optimal Concentration) Output->Interpretation

Caption: Workflow for applying polynomial regression to agricultural data.

Regression for Categorical and Time-to-Event Data

Logistic Regression: Predicting Binary Outcomes

Logistic regression is a powerful statistical method for modeling the relationship between a set of independent variables and a binary dependent variable (an outcome with two categories, such as presence/absence of a disease).[6][10] Instead of predicting the value of the variable itself, logistic regression predicts the probability of the outcome occurring.[11]

Experimental Protocol: Developing a Diagnostic Model for a Disease

In clinical research, logistic regression is frequently used to develop diagnostic models that predict the likelihood of a patient having a particular disease based on various clinical and demographic factors.

  • Patient Cohort Selection: A cohort of patients is recruited, including individuals with a confirmed diagnosis of the disease of interest and a control group of healthy individuals.

  • Data Collection: For each patient, a set of predictor variables is collected. These can include demographic information (e.g., age, sex), clinical measurements (e.g., blood pressure, cholesterol levels), and biomarker data. The binary outcome variable (disease present/absent) is also recorded for each patient.

  • Model Building: A logistic regression model is built using the collected data. The model estimates the relationship between each predictor variable and the log-odds of having the disease.[12]

  • Model Evaluation and Interpretation: The performance of the model is evaluated using metrics such as accuracy, sensitivity, and specificity. The coefficients of the model are interpreted as odds ratios, which quantify the change in the odds of having the disease for a one-unit change in a predictor variable, holding other variables constant.[13][14]

Table 3: Logistic Regression Analysis for Disease Diagnosis

Predictor VariableCoefficient (log-odds)Odds Ratio95% Confidence Interval for Odds Ratiop-value
Age (per year)0.051.05(1.02, 1.08)<0.001
Biomarker X (per unit)1.203.32(2.50, 4.40)<0.001
Treatment (Active vs. Placebo)-0.690.50(0.35, 0.71)<0.001

Logical Relationship: Logistic Regression Workflow for Diagnostics

logistic_regression_workflow Data Patient Data (Predictors and Disease Status) Model Logistic Regression Model (Predicts Probability of Disease) Data->Model Output Model Output (Odds Ratios, p-values) Model->Output Interpretation Interpretation (Identify Risk Factors) Output->Interpretation

Caption: Workflow for developing a diagnostic model using logistic regression.

Cox Proportional Hazards Model: Analyzing Time-to-Event Data

The Cox proportional hazards model is a regression method used for investigating the relationship between the survival time of patients and one or more predictor variables.[15][16] It is particularly useful in clinical trials and observational studies where the outcome of interest is the time until an event occurs, such as death, disease recurrence, or recovery.[17]

Experimental Protocol: Evaluating a New Cancer Therapy in a Clinical Trial

A common application of the Cox model is in oncology clinical trials to assess the efficacy of a new treatment compared to a standard treatment in terms of patient survival.[15]

  • Patient Enrollment and Randomization: A cohort of patients with a specific type of cancer is enrolled in the clinical trial. Patients are randomly assigned to receive either the new investigational therapy or the standard of care.

  • Follow-up and Event Monitoring: Patients in both treatment arms are followed over a specified period. The time from randomization until the occurrence of a predefined event (e.g., death, disease progression) is recorded for each patient. For patients who do not experience the event by the end of the study or are lost to follow-up, their data is "censored," meaning their survival time is known to be at least as long as their follow-up time.

  • Data Collection: In addition to time-to-event data, baseline characteristics of the patients (e.g., age, sex, tumor stage, biomarker status) are collected as covariates.

  • Cox Regression Analysis: A Cox proportional hazards model is fitted to the data. The model estimates the hazard ratio for the treatment effect, which represents the relative risk of the event occurring in the investigational treatment group compared to the standard treatment group, while adjusting for the effects of other covariates.[18] A hazard ratio less than 1 indicates that the new treatment is associated with a lower risk of the event.[19]

Table 4: Cox Proportional Hazards Model for Survival Analysis in an Oncology Trial

CovariateHazard Ratio95% Confidence Intervalp-value
Treatment (New vs. Standard)0.75(0.60, 0.94)0.012
Age (per 10-year increase)1.20(1.05, 1.37)0.008
Tumor Stage (Advanced vs. Early)2.50(1.80, 3.47)<0.001
Biomarker Status (Positive vs. Negative)0.60(0.45, 0.80)<0.001

Experimental Workflow: Clinical Trial with Survival Analysis

clinical_trial_workflow cluster_enrollment Patient Enrollment cluster_treatment Treatment Arms Enrollment Patient Cohort Randomization Randomization Enrollment->Randomization NewTx Investigational Treatment Randomization->NewTx StdTx Standard of Care Randomization->StdTx FollowUp Follow-up (Time-to-Event Data) NewTx->FollowUp StdTx->FollowUp Analysis Cox Proportional Hazards Analysis FollowUp->Analysis Results Results (Hazard Ratios) Analysis->Results

Caption: Workflow of a clinical trial with time-to-event data analysis.

Advanced and Machine Learning-Based Regression Models

Non-Linear Regression: Modeling Complex Biological Processes

Non-linear regression is used when the relationship between the independent and dependent variables cannot be described by a linear model.[20] In drug development, it is frequently used to model dose-response curves and enzyme kinetics.[16]

Experimental Protocol: Determining the IC50 of a Drug Candidate

A crucial step in drug discovery is determining the half-maximal inhibitory concentration (IC50) of a compound, which is the concentration of a drug that is required for 50% inhibition in vitro. This is typically done using non-linear regression to fit a sigmoidal dose-response curve.[21]

  • Assay Setup: A biological assay is set up to measure the activity of a target (e.g., an enzyme or a cell line).

  • Serial Dilution and Treatment: The drug candidate is serially diluted to create a range of concentrations. The target is then treated with these different concentrations of the drug.

  • Response Measurement: The biological response (e.g., enzyme activity, cell viability) is measured at each drug concentration.

  • Data Analysis: The drug concentrations (typically log-transformed) are plotted against the corresponding responses. A non-linear regression model, often a four-parameter logistic model, is fitted to the data to generate a sigmoidal curve.[20] The IC50 value is then derived from this curve.

Table 5: Non-Linear Regression for IC50 Determination

Log(Drug Concentration [M])% Inhibition (Observed)% Inhibition (Predicted)
-92.11.8
-815.416.2
-748.950.1
-685.284.5
-598.798.9
Derived IC50 (nM) -50.1

Signaling Pathway: Drug-Target Inhibition

drug_target_inhibition Drug Drug Target Biological Target (e.g., Enzyme) Drug->Target Inhibits Response Biological Response Target->Response Leads to

Caption: Simplified signaling pathway of drug-target inhibition.

Support Vector Regression (SVR): A Machine Learning Approach

Support Vector Regression (SVR) is a supervised learning algorithm that can be used for regression tasks.[22] It is particularly useful for high-dimensional data and can model non-linear relationships using different kernel functions.[23]

Experimental Protocol: Quantitative Structure-Activity Relationship (QSAR) Modeling

In drug discovery, SVR is often employed in Quantitative Structure-Activity Relationship (QSAR) studies to predict the biological activity of chemical compounds based on their molecular descriptors.[13][24]

  • Dataset Compilation: A dataset of chemical compounds with known biological activities (e.g., binding affinity, toxicity) is compiled.

  • Molecular Descriptor Calculation: For each compound, a set of numerical features, known as molecular descriptors, are calculated. These descriptors represent various physicochemical and structural properties of the molecules.

  • Model Training: An SVR model is trained on a subset of the data (the training set). The model learns the relationship between the molecular descriptors and the biological activity.

  • Model Validation: The trained SVR model is then used to predict the biological activity of the remaining compounds (the test set). The performance of the model is evaluated by comparing the predicted activities with the experimentally determined values.

Table 6: Support Vector Regression for QSAR Modeling

Compound IDMolecular WeightLogPNumber of Hydrogen Bond DonorsPredicted Bioactivity (pIC50)
Cmpd-001350.42.527.8
Cmpd-002412.53.136.5
Cmpd-003298.31.818.2
Cmpd-004450.64.225.9
Cmpd-005388.42.947.1

Logical Relationship: SVR-based QSAR Workflow

svr_qsar_workflow Data Chemical Data (Descriptors & Activity) Model Support Vector Regression Model Data->Model Output Predicted Bioactivity Model->Output Validation Model Validation Output->Validation

Caption: Workflow for QSAR modeling using Support Vector Regression.

Ridge and Lasso Regression: Handling High-Dimensional Data

Ridge and Lasso regression are regularization techniques used to handle multicollinearity and prevent overfitting in models with a large number of predictor variables, which is common in genomics and other high-throughput biological studies.[25] Lasso has the additional property of performing feature selection by shrinking the coefficients of less important variables to zero.[26]

Experimental Protocol: Identifying Prognostic Genes from Gene Expression Data

In cancer research, Lasso regression can be used to identify a small subset of genes from a large gene expression dataset that are most predictive of patient prognosis.[9]

  • Patient Cohort and Sample Collection: Tumor samples and corresponding clinical data (including survival information) are collected from a cohort of cancer patients.

  • Gene Expression Profiling: The expression levels of thousands of genes in each tumor sample are measured using techniques such as microarray or RNA-sequencing.

  • Data Preprocessing: The gene expression data is preprocessed and normalized.

  • Lasso Regression Analysis: A Lasso regression model is applied to the gene expression data, with patient survival as the outcome variable. The model selects a subset of genes with non-zero coefficients, which are considered to be the most important predictors of survival.

  • Prognostic Signature Development: The selected genes can be used to develop a prognostic signature that can classify patients into high-risk and low-risk groups.

Table 7: Gene Selection using Lasso Regression

Gene IDLasso CoefficientSelected for Prognostic Signature
Gene_A0.85Yes
Gene_B0.00No
Gene_C-0.42Yes
Gene_D0.00No
Gene_E0.67Yes

Experimental Workflow: Gene Selection with Lasso Regression

lasso_gene_selection_workflow cluster_data Data Acquisition cluster_analysis Data Analysis Samples Patient Samples Expression Gene Expression Profiling Samples->Expression Preprocessing Data Preprocessing Expression->Preprocessing Lasso Lasso Regression Preprocessing->Lasso Signature Prognostic Gene Signature Lasso->Signature Validation Validation Signature->Validation

Caption: Workflow for identifying a prognostic gene signature using Lasso regression.

Bayesian Regression: Incorporating Prior Knowledge

Bayesian regression methods provide a framework for incorporating prior knowledge into the modeling process.[14][27] This is particularly valuable in clinical trials where information from previous studies or expert opinion can be formally integrated into the analysis.[8]

Experimental Protocol: Bayesian Adaptive Design for a Phase I Dose-Finding Trial

In early-phase clinical trials, Bayesian methods are often used in adaptive designs to efficiently identify the maximum tolerated dose (MTD) of a new drug.[24][28]

  • Trial Design and Prior Specification: A dose-escalation scheme is defined, and a prior distribution for the probability of dose-limiting toxicity (DLT) at each dose level is specified based on preclinical data or previous experience with similar drugs.

  • Patient Enrollment in Cohorts: Patients are enrolled in small cohorts and treated at a specific dose level.

  • Toxicity Assessment: After a predefined observation period, the number of patients experiencing a DLT in the cohort is recorded.

  • Bayesian Model Updating: The observed toxicity data is used to update the prior distribution, resulting in a posterior distribution for the probability of DLT at each dose level.

  • Adaptive Dose Escalation: The posterior distribution is used to guide the decision for the next cohort of patients, which may involve escalating the dose, de-escalating the dose, or enrolling more patients at the current dose. This process is repeated until the MTD is identified.[18]

Table 8: Bayesian Dose-Finding Trial Decision Matrix

Number of Patients at Current DoseNumber of Patients with DLTDecision for Next Cohort
30Escalate to next dose level
31Enroll more patients at current dose
32 or 3De-escalate to lower dose level
61Escalate to next dose level
62 or moreDe-escalate to lower dose level

Logical Relationship: Bayesian Adaptive Trial Workflow

bayesian_adaptive_workflow Start Start Trial (Prior Beliefs) Enroll Enroll Patient Cohort Start->Enroll Treat Treat at Current Dose Enroll->Treat Observe Observe Toxicity Treat->Observe Update Update Beliefs (Posterior Distribution) Observe->Update Decision Dose Escalation/De-escalation Decision Update->Decision Decision->Enroll Continue Trial End Identify MTD Decision->End Stop Trial

Caption: Workflow of a Bayesian adaptive dose-finding clinical trial.

This guide provides a foundational understanding of various regression models and their applications in scientific research and drug development. The choice of the most appropriate model depends on the specific research question, the nature of the data, and the underlying assumptions of the model. By carefully selecting and applying these powerful analytical tools, researchers can extract meaningful insights from their data and accelerate the pace of scientific discovery.

References

The Role of Regression in Quantifying Relationships Between Variables: A Technical Guide

Author: BenchChem Technical Support Team. Date: December 2025

Introduction

Regression analysis is a cornerstone of statistical modeling, providing a powerful framework for researchers, scientists, and drug development professionals to quantify the relationship between a dependent variable and one or more independent variables.[1][2][3] Its applications span the entire drug development lifecycle, from early-stage discovery to post-market analysis. Regression enables the exploration of complex biological systems, the prediction of treatment outcomes, and the identification of key factors influencing experimental results.[4][5][6] This guide delves into the core principles of regression, outlines various techniques, presents a practical experimental protocol, and illustrates key workflows.

At its core, regression analysis helps to understand how the typical value of the dependent variable (or 'outcome' variable) changes when any one of the independent variables is varied, while the other independent variables are held fixed.[2] For example, in a clinical trial, regression can be used to determine how a patient's response to a drug (dependent variable) is influenced by factors like dosage, age, and biomarkers (independent variables).[4][7] It is crucial to remember that while regression can reveal strong associations, it does not inherently prove causation.[7][8]

Core Concepts of Regression

To effectively utilize regression analysis, a clear understanding of its fundamental components is essential.

  • Dependent Variable (Y): This is the main outcome or factor you are trying to predict or understand.[2][9][10] In biomedical research, this could be drug efficacy, tumor size, blood pressure, or the presence or absence of a disease.

  • Independent Variables (X): These are the factors that you hypothesize have an impact on your dependent variable.[2][9][10] Examples include drug dosage, patient demographics, gene expression levels, or environmental exposures.

  • Regression Equation: The relationship between variables is mathematically described by a regression equation. For a simple linear regression, the formula is:

    Y = β₀ + β₁X + ε[11]

    • Y: The dependent variable.

    • X: The independent variable.

    • β₀ (Intercept): The estimated value of Y when X is 0.[11]

    • β₁ (Coefficient/Slope): Represents the estimated change in Y for a one-unit increase in X.[11]

    • ε (Error Term): The part of Y that is not explained by X, accounting for variability in the data.[7]

A primary goal of regression is to estimate the values of the coefficients (β) that best fit the data.

General Regression Workflow

The process of building and interpreting a regression model follows a logical sequence of steps, from data preparation to the final application of insights.

A Problem Definition (Identify Variables) B Data Collection & Pre-processing A->B C Exploratory Data Analysis (e.g., Scatterplots) B->C D Model Selection (Choose Regression Type) C->D E Model Training (Estimate Coefficients) D->E F Model Evaluation (Assess Performance, e.g., R-squared) E->F G Interpretation of Results (Analyze Coefficients & p-values) F->G H Application & Prediction G->H

Caption: A generalized workflow for conducting regression analysis.

Types of Regression Models

The choice of regression technique depends heavily on the nature of the variables and the relationship being investigated.[3][11] The following table summarizes several common regression models used in scientific and pharmaceutical research.

Model Type Dependent Variable Type Description & Use Case
Simple/Multiple Linear Regression ContinuousModels a linear relationship between a continuous outcome and one (simple) or more (multiple) independent variables.[4][11][12] Use Case: Predicting blood pressure based on weight and age.
Logistic Regression Binary/CategoricalPredicts the probability of a categorical outcome (e.g., success/failure, yes/no).[7][13] Use Case: Predicting the likelihood of a patient responding to a treatment.
Polynomial Regression ContinuousCaptures non-linear relationships by fitting the data to a polynomial equation.[3] Use Case: Modeling dose-response curves that are not linear.
Stepwise Regression Continuous/CategoricalAn automated method for selecting the most significant independent variables to include in a model.[12] Use Case: Identifying key predictive biomarkers from a large panel.
Ridge & Lasso Regression ContinuousUsed when independent variables are highly correlated (multicollinearity) to prevent overfitting by penalizing large coefficients.[3] Use Case: Genomic studies with many correlated gene expression predictors.
Poisson Regression Count DataModels an outcome variable that represents a count of events.[4][13] Use Case: Analyzing the number of adverse event reports for a drug per month.
Cox Proportional Hazards Regression Time-to-EventA survival analysis method that models the time until an event of interest occurs.[13] Use Case: Assessing the effect of a new cancer therapy on patient survival time.

Decision Framework for Model Selection

Choosing the appropriate regression model is critical for obtaining valid results. The following diagram provides a simplified decision-making framework.

A Start: Define Dependent Variable (Outcome) B Continuous? A->B C Count Data? B->C No J Is relationship linear? B->J Yes D Binary/Categorical? C->D No G Poisson Regression C->G Yes E Time-to-Event? D->E No H Logistic Regression D->H Yes I Cox Regression E->I Yes F Linear Regression J->F Yes K Polynomial or other non-linear regression J->K No

Caption: A decision tree for selecting a suitable regression model.

Experimental Protocol: Quantitative Structure-Activity Relationship (QSAR) Modeling

QSAR is a computational modeling method that uses regression to predict the biological activity of chemical compounds based on their physicochemical properties.[5] It is a critical tool in drug discovery for optimizing lead compounds and prioritizing candidates for synthesis.[5]

Objective: To develop a robust regression model that quantitatively links the structural features of a series of compounds to their measured biological activity.

Methodology:

  • Data Curation:

    • Assemble a dataset of at least 30-50 structurally diverse compounds with experimentally determined biological activity (e.g., IC₅₀, Ki). This will serve as the dependent variable (Y).

    • Ensure data consistency, converting all activity values to a uniform scale (e.g., pIC₅₀ = -log(IC₅₀)).

  • Descriptor Calculation:

    • For each compound, calculate a set of molecular descriptors that quantify its structural, physicochemical, and electronic properties. These are the independent variables (X).

    • Common descriptors include: Molecular Weight (MW), LogP (lipophilicity), Number of Hydrogen Bond Donors/Acceptors, and Topological Polar Surface Area (TPSA).

    • Use specialized software (e.g., RDKit, MOE, Dragon) for descriptor calculation.

  • Data Splitting:

    • Randomly partition the dataset into a training set (typically 70-80% of the data) and a test set (20-30%).

    • The training set is used to build the regression model. The test set is used for external validation to assess its predictive power on unseen data.

  • Model Building and Selection:

    • Using the training set, apply a suitable regression technique. Multiple Linear Regression (MLR) is a common starting point. If multicollinearity is suspected among descriptors, Ridge or Lasso regression may be more appropriate.

    • Employ a variable selection method, such as stepwise regression, to identify the most relevant descriptors and avoid overfitting.[12]

  • Model Validation:

    • Internal Validation: Perform cross-validation (e.g., leave-one-out) on the training set to assess the model's robustness.

    • External Validation: Use the trained model to predict the activity of the compounds in the test set.

    • Calculate key performance metrics:

      • Coefficient of Determination (R²): Should be > 0.6 for the test set.

      • Root Mean Square Error (RMSE): Measures the average prediction error.

  • Interpretation:

    • Analyze the final regression equation. The coefficients of the selected descriptors indicate the direction and magnitude of their influence on biological activity. For example, a positive coefficient for LogP suggests that increasing lipophilicity enhances activity.

cluster_0 Data Preparation cluster_1 Model Development & Validation cluster_2 Application A Assemble Compound Dataset (with Activity) B Calculate Molecular Descriptors (X variables) A->B C Split Data (Training & Test Sets) B->C D Train Regression Model on Training Set C->D E Internal Validation (Cross-Validation) D->E F External Validation on Test Set D->F G Interpret Model (Analyze Coefficients) F->G H Predict Activity of New Compounds G->H

Caption: A workflow diagram for QSAR modeling in drug discovery.

Applications in Drug Development and Research

Regression analysis is indispensable across various domains of pharmaceutical science.

  • Stability Analysis: Linear regression is used to model drug degradation over time, allowing for the accurate estimation of a product's shelf-life based on stability study data.[14]

  • Clinical Trials: Multiple regression helps identify which patient characteristics (e.g., age, biomarkers, comorbidities) are significant predictors of treatment response or adverse events.[4][10]

  • Sales and Marketing: Forecasting models use regression to predict future drug sales based on variables like marketing expenditure, competitor actions, and clinical trial outcomes.[13]

  • Biomedical Research: Researchers use regression to investigate associations between risk factors (e.g., lifestyle, genetic markers) and disease incidence.[4]

Regression analysis is a versatile and essential statistical tool for researchers and drug development professionals. It provides a quantitative method to describe, predict, and test hypotheses about the relationships between variables.[1][11] From optimizing lead compounds in discovery to interpreting clinical trial results, its proper application enables data-driven decision-making, enhances research insights, and ultimately contributes to the development of safer and more effective medicines. The key to successful regression analysis lies in selecting the appropriate model, rigorously validating its performance, and correctly interpreting the results within the context of the scientific question at hand.[3]

References

The Precision of Prediction: A Technical Guide to Regression Analysis in Scientific Forecasting

Author: BenchChem Technical Support Team. Date: December 2025

An In-depth Guide for Researchers, Scientists, and Drug Development Professionals

In the vanguard of scientific discovery and therapeutic innovation, the ability to accurately predict outcomes is paramount. From forecasting disease progression to estimating the efficacy of novel drug compounds, predictive modeling serves as a cornerstone of modern research. Among the most powerful and versatile tools in the predictive arsenal (B13267) is regression analysis. This technical guide provides a comprehensive overview of the core principles and applications of regression analysis for prediction and forecasting in scientific domains, with a particular focus on its utility in drug development.

Core Concepts of Regression Analysis in Scientific Prediction

Regression analysis is a statistical methodology for estimating the relationship between a dependent variable and one or more independent variables.[1] In the context of scientific prediction, the goal is to build a model that can accurately forecast the value of a dependent variable (the outcome of interest) based on the values of the independent variables (the predictors).[2]

The fundamental premise of using regression for prediction is to identify and quantify the relationships within a dataset to forecast future or unobserved outcomes.[2][3] This process involves developing a mathematical equation that represents the relationship between the variables.[4]

Types of Regression Models in Scientific Research:

The choice of regression model is dictated by the nature of the dependent variable.[5]

  • Linear Regression: Used when the dependent variable is continuous and the relationship between the dependent and independent variables is assumed to be linear.[4] A common application is in Quantitative Structure-Activity Relationship (QSAR) models, where the biological activity of a compound (a continuous value) is predicted based on its physicochemical properties.[6]

  • Multiple Linear Regression: An extension of simple linear regression that uses multiple independent variables to predict a single continuous dependent variable.[4] For instance, predicting a patient's blood pressure based on age, weight, and dosage of a medication.[4]

  • Logistic Regression: Employed when the dependent variable is binary or categorical (e.g., success/failure, presence/absence of a disease).[4] This is widely used in clinical research to predict outcomes like the probability of a patient responding to a treatment or the likelihood of a clinical trial's success.[7]

  • Non-Linear Regression: Utilized when the relationship between the dependent and independent variables is not linear.[6] This can be relevant in modeling complex biological processes that do not follow a straight-line trend.

  • Cox Proportional-Hazards Model: A regression model commonly used in survival analysis to investigate the effect of several variables on the time it takes for an event of interest to happen.[8] In drug development, it can be used to predict the time to disease progression or patient survival.

Methodologies and Experimental Protocols

The development of a robust regression model for scientific prediction is a systematic process that involves careful planning, execution, and validation.[9]

Experimental Protocol for Developing a Clinical Prediction Model

The following protocol outlines the key steps in creating a regression-based clinical prediction model, for example, to predict patient response to a new drug.[6][10]

  • Define the Research Question and Outcome: Clearly articulate the prediction goal. For instance, "To predict the probability of a patient with metastatic melanoma responding to a new immunotherapy based on baseline gene expression levels in their tumor." The outcome is binary (responder/non-responder), suggesting logistic regression.[11]

  • Data Collection and Preparation:

    • Source of Data: Ideally, data should be from a prospectively collected cohort.[11] However, existing data from clinical trials or other relevant studies are often used.[12]

    • Define Predictor Variables: Select potential predictors based on existing literature and clinical expertise. In our example, this would be the expression levels of a panel of genes.

    • Data Curation: Handle missing data through appropriate imputation techniques (e.g., multiple imputation).[12] Ensure data quality and consistency.

  • Model Development:

    • Data Splitting: Divide the dataset into a training set (for building the model) and a testing set (for evaluating its performance).[11]

    • Variable Selection: Employ statistical techniques (e.g., stepwise regression, LASSO) to identify the most significant predictors from the initial panel of genes.

    • Model Fitting: Fit the chosen regression model (e.g., logistic regression) to the training data.

  • Model Validation:

    • Internal Validation: Assess the model's performance on the testing set using metrics like the Area Under the Receiver Operating Characteristic Curve (AUC-ROC), sensitivity, and specificity.[11]

    • External Validation: Test the model on an independent dataset from a different population or time period to ensure generalizability.[11]

  • Model Application and Interpretation: Once validated, the model can be used to predict the probability of response for new patients. The coefficients of the regression equation provide insights into the strength and direction of the relationship between each predictor gene and the likelihood of response.

Experimental Protocol for QSAR Model Development

Quantitative Structure-Activity Relationship (QSAR) models are a cornerstone of modern drug discovery, used to predict the biological activity of chemical compounds.[2]

  • Data Collection and Curation:

    • Dataset Assembly: Compile a dataset of chemical compounds with their known biological activities (e.g., IC50 values) against a specific target.

    • Structural and Physicochemical Descriptors: For each compound, calculate a range of molecular descriptors (e.g., molecular weight, logP, topological indices) that will serve as the independent variables.

    • Data Cleaning: Remove duplicates, correct structural errors, and handle missing data.[9]

  • Model Building:

    • Training and Test Set Division: Split the dataset into training and test sets.[9]

    • Feature Selection: Use techniques like genetic algorithms or recursive feature elimination to select the most informative descriptors.

    • Regression Model Selection: Choose an appropriate regression model, often multiple linear regression or machine learning-based regression methods like support vector regression.[13]

    • Model Generation: Train the regression model on the training set.

  • Rigorous Model Validation:

    • Internal Validation: Use cross-validation on the training set to assess the model's robustness.

    • External Validation: Evaluate the model's predictive power on the unseen test set.[9]

    • Applicability Domain Definition: Define the chemical space for which the model's predictions are reliable.[9]

  • Prediction and Virtual Screening:

    • The validated QSAR model can then be used to predict the activity of new, untested compounds, enabling the prioritization of candidates for synthesis and experimental testing.[2]

Data Presentation: Quantitative Model Performance

The performance of regression models is assessed using various quantitative metrics. The following tables provide an illustrative summary of performance metrics for different regression models used in drug response prediction, based on findings from comparative analyses using datasets like the Genomics of Drug Sensitivity in Cancer (GDSC).[13][14]

Regression Model Feature Set Pearson Correlation Coefficient (PCC) Root Mean Square Error (RMSE)
Support Vector RegressionGene Expression (L1000)0.681.25
Ridge RegressionGene Expression (Full Genome)0.651.32
ElasticNetGene Expression + Mutations0.621.40
Random Forest RegressionGene Expression (L1000)0.661.29

Table 1: Illustrative performance of different regression algorithms in predicting drug sensitivity (IC50 values) based on genomic features. Higher PCC and lower RMSE indicate better performance.

Model Evaluation Metric Description Typical Value Range (Good Model)
R-squared (R²) The proportion of the variance in the dependent variable that is predictable from the independent variables.> 0.6
Adjusted R-squared A modified version of R² that adjusts for the number of predictors in the model.Close to R²
Mean Squared Error (MSE) The average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value.Lower is better
Area Under the Curve (AUC-ROC) For logistic regression, it represents the model's ability to distinguish between positive and negative classes.> 0.7

Table 2: Key evaluation metrics for regression models in a scientific context.

Visualizing Predictive Relationships and Workflows

Diagrams are essential for illustrating the logical flow of experiments and the complex interplay of variables in predictive models.

Signaling Pathway for Drug Response Prediction

The following diagram illustrates how the expression levels of genes within a simplified cancer-related signaling pathway can be used as independent variables in a regression model to predict a cellular phenotype, such as sensitivity to a targeted therapy.

G cluster_input Independent Variables (Gene Expression) cluster_model Predictive Model cluster_output Dependent Variable (Predicted Outcome) GeneA Gene A (e.g., Receptor) GeneB Gene B (e.g., Kinase) GeneA->GeneB Regression Regression Model (e.g., Logistic Regression) GeneA->Regression GeneC Gene C (e.g., Transcription Factor) GeneB->GeneC GeneB->Regression GeneC->Regression Phenotype Cellular Phenotype (e.g., Drug Sensitivity) Regression->Phenotype caption Predicting phenotype from signaling pathway gene expression.

Caption: Predicting phenotype from signaling pathway gene expression.

Experimental Workflow for QSAR Model Development

This diagram outlines the systematic workflow for developing and validating a QSAR model for the prediction of compound activity.

G cluster_data Data Preparation cluster_model Model Development & Validation cluster_application Application A 1. Collect Compound Data (Structures & Activities) B 2. Calculate Molecular Descriptors A->B C 3. Curate and Split Data (Training & Test Sets) B->C D 4. Select Features & Regression Algorithm C->D E 5. Train Model on Training Set D->E F 6. Validate Model on Test Set E->F G 7. Define Applicability Domain F->G H 8. Predict Activity of New Compounds (Virtual Screening) G->H caption Workflow for developing a predictive QSAR model.

References

Methodological & Application

Application Notes and Protocols: Performing Multiple Regression Analysis in SPSS for Research

Author: BenchChem Technical Support Team. Date: December 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction to Multiple Regression Analysis

Multiple regression is a statistical technique used to understand the relationship between a single dependent variable and two or more independent variables.[1][2][3] It allows researchers to predict the value of a dependent variable based on the values of the predictor variables and to determine the relative contribution of each predictor to the overall variance explained in the dependent variable.[1] For instance, in drug development, multiple regression could be used to predict treatment efficacy (the dependent variable) based on factors like dosage, patient age, and specific biomarker levels (the independent variables).

The fundamental model is expressed through a regression equation: Y = b₀ + b₁X₁ + b₂X₂ + ... + bₙXₙ + ε[4]

Where:

  • Y is the dependent variable.

  • X₁...Xₙ are the independent variables.

  • b₀ is the intercept (the value of Y when all X variables are 0).

  • b₁...bₙ are the regression coefficients, representing the change in Y for a one-unit change in the respective X variable, holding all other variables constant.[5]

  • ε is the error term.

Key Assumptions of Multiple Regression

Before conducting a multiple regression analysis, it is crucial to ensure your data meets several assumptions to ensure the validity and reliability of the results.[1][3]

  • Linear Relationship: There must be a linear relationship between the dependent variable and each independent variable, as well as collectively.[1][6] This can be checked by creating scatterplots of each independent variable against the dependent variable.

  • Independence of Observations: The residuals (the differences between observed and predicted values) should be independent. The Durbin-Watson statistic is used to test this, with values ideally around 2.[1][6]

  • Homoscedasticity: The variance of the residuals should be constant across all levels of the predicted values.[1] This can be visually inspected using a scatterplot of the standardized predicted values versus the standardized residuals.[6][7]

  • Normality of Residuals: The residuals of the regression model should be approximately normally distributed.[7] This can be checked with a histogram or a P-P plot of the standardized residuals.[1]

  • No Multicollinearity: The independent variables should not be too highly correlated with each other.[1][8] High multicollinearity can make it difficult to determine the individual contribution of each predictor. This is assessed using Tolerance and Variance Inflation Factor (VIF) values. A Tolerance value below 0.2 or a VIF value above 10 may indicate a problem.[6]

  • No Significant Outliers: There should be no influential outliers that could unduly affect the regression model.[1]

Experimental Protocol: Step-by-Step Multiple Regression in SPSS

This protocol outlines the procedure for conducting a multiple regression analysis and checking its assumptions using SPSS.

  • Open SPSS and Load Data: Launch SPSS and load your dataset. Ensure your data is properly formatted, with one continuous dependent variable and two or more independent variables (which can be continuous or dichotomous).[2][4]

  • Navigate to the Linear Regression Dialog Box:

    • From the top menu, click Analyze > Regression > Linear... [1][3][4]

  • Assign Variables:

    • In the "Linear Regression" dialog box, select your dependent variable and move it to the Dependent: box.

    • Select your independent variables and move them to the Independent(s): box.[2][9]

  • Set Statistical Options for Assumption Checking:

    • Click the Statistics... button.

    • In the "Linear Regression: Statistics" sub-dialog box, check the following boxes:

      • Estimates (selected by default)

      • Confidence intervals [1][10]

      • Model fit (selected by default)

      • Descriptives

      • Collinearity diagnostics

      • Durbin-Watson [10]

    • Click Continue .

  • Create Plots for Residual Analysis:

    • Click the Plots... button.

    • In the "Linear Regression: Plots" sub-dialog box:

      • Move *ZRESID (Standardized Residuals) to the Y: box.

      • Move *ZPRED (Standardized Predicted Values) to the X: box. This plot is used to check for homoscedasticity and linearity.[4]

      • Check the boxes for Histogram and Normal probability plot to assess the normality of residuals.

    • Click Continue .

  • Run the Analysis:

    • Click OK in the main "Linear Regression" dialog box to execute the analysis. The results will be generated in the SPSS Output Viewer.[2]

Data Presentation: Interpreting the SPSS Output

The SPSS output for multiple regression consists of several key tables. Understanding these tables is essential for interpreting the results of your analysis.

This table provides an overview of the model's overall fit.

StatisticDescriptionInterpretation Example
R The multiple correlation coefficient. It indicates the strength of the linear relationship between the predicted and observed values of the dependent variable.An R value of 0.850 indicates a strong positive relationship.[1]
R Square (R²) The coefficient of determination. It represents the proportion of variance in the dependent variable that can be explained by the independent variables.An R² of 0.722 means that 72.2% of the variance in the dependent variable is explained by the model.[2][9][11]
Adjusted R Square An adjusted version of R² that accounts for the number of predictors in the model. It is generally considered a more accurate measure of model fit, especially with multiple predictors.An Adjusted R² of 0.715 suggests that after adjusting for the number of predictors, the model explains 71.5% of the variance.[2][12]
Std. Error of the Estimate The average distance that the observed values fall from the regression line. A smaller value indicates a better model fit.This value represents the standard deviation of the residuals.[5]
Durbin-Watson Tests for the independence of residuals.A value of 1.93 suggests that the assumption of independent errors has been met.[6]

The ANOVA (Analysis of Variance) table indicates whether the overall regression model is statistically significant.

StatisticDescriptionInterpretation Example
F The F-statistic, which is the ratio of the mean square regression to the mean square residual.A large F value indicates that the variation explained by the model is large relative to the unexplained variation.
Sig. (p-value) The p-value associated with the F-statistic.A p-value less than 0.05 (e.g., p < .001) indicates that the overall regression model is statistically significant and a good fit for the data.[1][10]

This is the most important table, providing detailed information about each predictor's contribution to the model.

StatisticDescriptionInterpretation Example
(Constant) The Y-intercept (b₀) of the regression equation.The predicted value of the dependent variable when all independent variables are zero.[9]
Unstandardized B The unstandardized regression coefficients (b₁, b₂, etc.). Represents the change in the dependent variable for a one-unit increase in the predictor, holding others constant.A B of 2.5 for 'Dosage' means that for every one-unit increase in dosage, the dependent variable is predicted to increase by 2.5 units.[7][9][12]
Std. Error The standard error of the unstandardized B coefficient.Smaller values indicate more precise estimates of the coefficient.
Standardized Beta (β) The standardized regression coefficients. They are used to compare the relative strength of the predictors.A Beta of 0.6 for 'Dosage' and 0.3 for 'Age' indicates that 'Dosage' has a stronger effect on the outcome than 'Age'.
t The t-statistic, used to test the significance of individual predictor variables.Calculated by dividing the B coefficient by its standard error.
Sig. (p-value) The p-value for each t-statistic.A p-value less than 0.05 indicates that the predictor variable is a statistically significant contributor to the model.[12]
Collinearity Statistics Includes Tolerance and VIF values to check for multicollinearity.VIF values below 10 and Tolerance values above 0.2 indicate that the assumption of no multicollinearity is met.[6]

Mandatory Visualizations

The following diagrams illustrate the conceptual framework and workflow of a multiple regression analysis.

G cluster_ivs Independent Variables (Predictors) IV1 X₁ (e.g., Dosage) DV Y Dependent Variable (e.g., Treatment Efficacy) IV1->DV β₁ IV2 X₂ (e.g., Age) IV2->DV β₂ IVn Xₙ (e.g., Biomarker) IVn->DV βₙ

Caption: Conceptual model of multiple regression.

G start Start: Define Research Question and Variables assumptions Check Assumptions: 1. Linearity 2. Normality 3. Homoscedasticity 4. Multicollinearity start->assumptions spss_setup SPSS Protocol: Analyze > Regression > Linear assumptions->spss_setup assign_vars Assign Dependent & Independent Variables spss_setup->assign_vars set_options Set 'Statistics' & 'Plots' Options (e.g., Durbin-Watson, VIF, Residual Plots) assign_vars->set_options run Execute Analysis set_options->run output Review SPSS Output Tables: - Model Summary - ANOVA - Coefficients run->output interpret Interpret Results: - Overall model fit (R², F-test) - Individual predictor significance (p-values) - Effect size and direction (B, Beta) output->interpret report Report Findings interpret->report

Caption: Workflow for multiple regression analysis in SPSS.

References

Application Notes and Protocols for Logistic Regression in Clinical Trials with Binary Outcomes

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

These application notes provide a detailed guide on the use of logistic regression for analyzing binary outcomes in clinical trials. The content covers the theoretical basis, practical application, and interpretation of results, using a relevant clinical trial example involving an mTOR inhibitor.

Introduction to Logistic Regression for Binary Outcomes

In clinical trials, researchers often encounter binary outcomes, such as whether a patient's tumor responded to treatment (yes/no), if a patient experienced a specific adverse event (yes/no), or if a patient's disease progressed (yes/no). Logistic regression is a powerful statistical method specifically designed to model the relationship between a set of predictor variables (e.g., treatment group, patient demographics, biomarkers) and a binary dependent variable.[1] Unlike linear regression, which predicts a continuous outcome, logistic regression predicts the probability of an event occurring.[1]

The core of logistic regression is the logistic function, which transforms a linear combination of predictor variables into a value between 0 and 1, representing the probability of the outcome of interest. The model estimates the odds ratio for each predictor variable, which quantifies the strength of the association between the predictor and the outcome.[2] An odds ratio greater than 1 indicates that the predictor increases the odds of the outcome occurring, while an odds ratio less than 1 indicates a decrease in the odds.[2]

Application in a Clinical Trial Context: The Role of mTOR Inhibitors

To illustrate the application of logistic regression, we will consider a hypothetical clinical trial scenario based on the principles of studies like the BOLERO-2 trial, which investigated the efficacy of the mTOR inhibitor everolimus (B549166) in combination with exemestane (B1683764) for hormone receptor-positive advanced breast cancer.[3][4][5]

The PI3K/Akt/mTOR signaling pathway is a crucial regulator of cell growth, proliferation, and survival, and its aberrant activation is a hallmark of many cancers.[6][7][8][9][10] mTOR inhibitors like everolimus block this pathway, thereby inhibiting tumor growth.

Signaling Pathway of mTOR Inhibition

The following diagram illustrates the PI3K/Akt/mTOR signaling pathway and the point of intervention for an mTOR inhibitor like everolimus.

PI3K_Akt_mTOR_Pathway cluster_membrane cluster_cytoplasm cluster_nucleus RTK Receptor Tyrosine Kinase (RTK) PI3K PI3K RTK->PI3K PIP3 PIP3 PI3K->PIP3 phosphorylates PIP2 PIP2 PDK1 PDK1 PIP3->PDK1 Akt Akt PDK1->Akt activates mTORC1 mTORC1 Akt->mTORC1 activates S6K1 p70S6K mTORC1->S6K1 fourEBP1 4E-BP1 mTORC1->fourEBP1 Protein_Synthesis Protein Synthesis, Cell Growth, Proliferation S6K1->Protein_Synthesis fourEBP1->Protein_Synthesis Everolimus Everolimus (mTOR Inhibitor) Everolimus->mTORC1 inhibits

PI3K/Akt/mTOR Signaling Pathway Inhibition

Experimental Protocol for a Clinical Trial Utilizing Logistic Regression

The following protocol is a generalized example based on best practices such as the SPIRIT (Standard Protocol Items: Recommendations for Interventional Trials) and CONSORT (Consolidated Standards of Reporting Trials) guidelines.[6][7][8][9]

Study Design and Objectives

A Phase III, randomized, double-blind, placebo-controlled trial to evaluate the efficacy and safety of an mTOR inhibitor in combination with standard endocrine therapy for patients with advanced, hormone receptor-positive breast cancer.

  • Primary Objective: To compare the clinical benefit rate (CBR) between the mTOR inhibitor arm and the placebo arm. Clinical benefit is a binary outcome defined as a complete response, partial response, or stable disease for at least 24 weeks.

  • Secondary Objectives: To assess progression-free survival (PFS), overall survival (OS), safety and tolerability, and to identify predictive biomarkers of response.

Patient Population

  • Inclusion Criteria:

    • Postmenopausal women with a confirmed diagnosis of hormone receptor-positive, HER2-negative advanced breast cancer.

    • Evidence of disease progression after prior endocrine therapy.

    • Measurable disease as per RECIST criteria.

    • Adequate organ function.

  • Exclusion Criteria:

    • Prior treatment with an mTOR inhibitor.

    • Uncontrolled diabetes or other comorbidities that would contraindicate the use of an mTOR inhibitor.

Randomization and Blinding

Patients will be randomized in a 1:1 ratio to receive either the mTOR inhibitor or a matching placebo, in addition to standard endocrine therapy. Both patients and investigators will be blinded to the treatment allocation.

Intervention

  • Experimental Arm: Oral mTOR inhibitor (e.g., Everolimus 10 mg) once daily + standard endocrine therapy.

  • Control Arm: Oral placebo once daily + standard endocrine therapy.

Treatment will continue until disease progression or unacceptable toxicity.

Data Collection and Statistical Analysis

Clinical data, including tumor assessments, adverse events, and laboratory parameters, will be collected at baseline and at regular intervals throughout the study.

The primary analysis of the clinical benefit rate will be performed using a multivariable logistic regression model. The model will include treatment group as the primary predictor of interest, and will be adjusted for baseline prognostic factors such as age, performance status, and prior lines of therapy.

Data Presentation: Summarizing Logistic Regression Results

The results of the logistic regression analysis should be presented in a clear and structured table, including the odds ratio, 95% confidence interval, and p-value for each variable in the model.

Table 1: Multivariable Logistic Regression Analysis of Factors Associated with Adverse Events (Example from a study on Everolimus)

VariableOdds Ratio (OR)95% Confidence Interval (CI)p-value
Everolimus Trough Level (Quartile)
Quartile 1 (< 9.0 ng/mL)1.00 (Reference)--
Quartile 2 (9.0-12.9 ng/mL)2.081.12 - 3.850.02
Quartile 3 (12.9-22.8 ng/mL)2.631.42 - 4.870.002
Quartile 4 (> 22.8 ng/mL)1.951.03 - 3.680.04
Age (per 10-year increase) 1.150.98 - 1.350.09
Sex (Male vs. Female) 1.320.89 - 1.960.17
BMI (per 5 kg/m ² increase) 1.080.92 - 1.270.35

This table is a representative example based on findings from a pharmacokinetic analysis of everolimus where logistic regression was used to model adverse event outcomes.[9]

Experimental Workflow and Logical Relationships

The following diagram illustrates the workflow of a patient through the clinical trial and the logical relationship leading to the binary outcome analysis.

Clinical_Trial_Workflow Screening Patient Screening (Inclusion/Exclusion Criteria) Consent Informed Consent Screening->Consent Randomization Randomization (1:1) Consent->Randomization ArmA Treatment Arm A: mTOR Inhibitor + Endocrine Therapy Randomization->ArmA 50% ArmB Treatment Arm B: Placebo + Endocrine Therapy Randomization->ArmB 50% FollowUp Follow-up & Data Collection (Tumor Assessments, AEs) ArmA->FollowUp ArmB->FollowUp Outcome Binary Outcome Assessment (e.g., Clinical Benefit) FollowUp->Outcome Analysis Logistic Regression Analysis Outcome->Analysis

Clinical Trial Workflow for Binary Outcome Analysis

Conclusion

Logistic regression is an indispensable tool for the analysis of binary outcomes in clinical trials. Its ability to provide odds ratios allows researchers to quantify the effect of an intervention while adjusting for potential confounding factors. By following standardized protocols and reporting guidelines, the results of such analyses can be presented clearly and transparently, contributing to the advancement of evidence-based medicine.

References

Application Notes: Utilizing Poisson Regression for Count Data in Ecological Research

Application Notes and Protocols: A Guide to Selecting Independent Variables for Regression Models

Author: BenchChem Technical Support Team. Date: December 2025

Audience: Researchers, scientists, and drug development professionals.

Objective: This document provides a structured approach and detailed protocols for selecting the appropriate independent variables (predictors) for a regression model. Proper variable selection is critical for creating a model that is not only accurate but also robust, interpretable, and generalizable, which is paramount in scientific research and drug development.

Foundational Principles in Variable Selection

Before initiating any statistical procedure, it is crucial to ground the variable selection process in two foundational principles: the integration of domain knowledge and the pursuit of model parsimony.

  • 1.1 The Primacy of Domain Knowledge: Statistical methods are powerful tools, but they cannot substitute for subject-matter expertise. Domain knowledge is essential for hypothesizing relationships, identifying candidate variables, interpreting model outputs, and recognizing results that may be statistically significant but practically meaningless.[1][2][3] In drug development, for example, understanding the biological mechanism of a compound can guide the selection of relevant biomarkers as predictors of patient response.[4] This expert-driven approach enhances the interpretability of the model and helps avoid overfitting by focusing on theoretically relevant variables.[1][5]

  • 1.2 The Principle of Parsimony (Occam's Razor): This principle states that among competing hypotheses, the one with the fewest assumptions should be selected. In modeling, this translates to favoring the simplest model that adequately explains the data.[6] Overly complex models with unnecessary predictors can be noisy, less generalizable, and more difficult to interpret.[6][7] The goal is to capture the true underlying relationship without fitting the noise in the data.

Overall Workflow for Variable Selection

The selection of independent variables should be a systematic process, not a one-time automated step. The following workflow diagram illustrates the key phases, integrating domain knowledge, data exploration, statistical methods, and rigorous validation.

Variable Selection Workflow A 1. Define Research Question & Hypothesis B 2. Candidate Variable Identification (Domain Knowledge & Literature Review) A->B C 3. Exploratory Data Analysis (EDA) (Data Cleaning, Visualization, Initial Screening) B->C D 4. Address Multicollinearity (VIF, Correlation Matrix) C->D E 5. Apply Automated Selection Methods (Stepwise, LASSO, etc.) D->E F 6. Generate Candidate Models E->F G 7. Evaluate & Compare Models (AIC, BIC, Adjusted R-squared) F->G G->E Iterate/Refine H 8. Validate Final Model (Cross-Validation on unseen data) G->H I 9. Final Model Interpretation (In context of Domain Knowledge) H->I

Caption: A systematic workflow for robust variable selection.

Protocol 1: Exploratory Data Analysis (EDA)

Objective: To understand the characteristics of the data, check assumptions, identify anomalies, and perform initial variable screening before formal modeling.[8][9]

Methodology:

  • Data Inspection:

    • Review the data types of each variable to ensure they are correctly coded (e.g., numeric, categorical).[8]

    • Check for and document missing data. Develop a strategy for handling them (e.g., imputation, removal), considering potential biases.[8][10]

  • Univariate Analysis:

    • For each continuous variable, generate histograms and box plots to visualize its distribution and identify potential outliers.[9][11] Skewed distributions may require transformation (e.g., logarithmic) to meet model assumptions.[10]

    • For categorical variables, use bar charts to understand the frequency of each level.

  • Bivariate Analysis:

    • Create a correlation matrix with heatmaps to visualize the linear relationships between all pairs of continuous independent variables.[10][11] This is a primary tool for spotting potential multicollinearity.

    • Generate scatter plots for each independent variable against the dependent (target) variable to visually inspect for linear relationships, which is a key assumption of linear regression.[12]

  • Initial Screening:

    • Based on the EDA, variables with very low variance (i.e., they are nearly constant) can often be removed.

    • Variables that show no plausible relationship with the target variable in bivariate plots may be flagged for potential exclusion, but this should be confirmed with domain knowledge.

Protocol 2: Detection and Management of Multicollinearity

Objective: To identify and address high correlation among independent variables, which can destabilize the model and make coefficient estimates unreliable.[13][14][15]

Background: Multicollinearity occurs when two or more independent variables are highly correlated, meaning they provide redundant information.[16][17] This inflates the variance of the coefficient estimates, making it difficult to determine the individual contribution of each predictor.[13][14]

Methodology:

  • Detection using Variance Inflation Factor (VIF): The VIF is the most common method for quantifying the severity of multicollinearity.[15][17]

    • Procedure: For each independent variable Xᵢ, fit a linear regression model that has Xᵢ as the dependent variable and all other independent variables as predictors.

    • Calculate the R² from this model, denoted as R²ᵢ.

    • The VIF for Xᵢ is calculated as: VIFᵢ = 1 / (1 - R²ᵢ).

    • Repeat this for every independent variable.

  • Interpretation of VIF: Use the following table to interpret the VIF values.

VIF ValueLevel of MulticollinearityRecommended Action
1NoneVariable is not correlated with others.
1 - 5ModerateGenerally acceptable, but may warrant further investigation.
> 5 - 10HighPotentially problematic; coefficients may be poorly estimated.[15]
> 10Very HighA cause for concern; indicates serious multicollinearity.

  • Resolution Strategies:

    • Variable Removal: The simplest approach is to remove one of the highly correlated variables. The choice should be guided by domain knowledge about which variable is more theoretically relevant or easier to measure.

    • Variable Combination: Create a new composite variable from the correlated predictors. For instance, in a clinical trial, 'height' and 'weight' could be combined to create 'Body Mass Index (BMI)'.

    • Use Regularization: Techniques like Ridge Regression are specifically designed to handle multicollinearity by shrinking the coefficients of correlated predictors.

Protocol 3: Automated Variable Selection Methods

Objective: To use algorithmic approaches to find the optimal subset of predictors from a larger set of candidate variables. These methods are powerful but should be used in conjunction with, not as a replacement for, domain knowledge.

Wrapper Methods

Wrapper methods use the performance of a specific machine learning algorithm to evaluate the utility of a subset of variables.[18]

Stepwise Selection Logic cluster_0 Forward Selection cluster_1 Backward Elimination A Start with Null Model (No predictors) B Test adding each variable individually A->B C Add the variable that provides the most statistically significant improvement B->C D Repeat until no variable addition provides significant improvement C->D D->C Iterate E Start with Full Model (All predictors) F Test removing each variable individually E->F G Remove the least statistically significant variable (if not significant) F->G H Repeat until all remaining variables are significant G->H H->G Iterate

Caption: Logic of Forward Selection and Backward Elimination.

  • Stepwise Selection: This is an iterative approach to building a model.[19]

    • Forward Selection: Starts with no variables in the model. In each step, it adds the most statistically significant variable until no further additions provide a significant improvement.[6][20][21]

    • Backward Elimination: Starts with all candidate variables in the model. In each step, it removes the least significant variable until all remaining variables are statistically significant.[6][20][21]

    • Bidirectional (Stepwise) Elimination: A combination of the above, where variables are added and removed at each step to find an optimal model.[20]

Embedded (Shrinkage) Methods

These methods perform variable selection as part of the model fitting process itself. They are particularly useful for high-dimensional data (many predictors).

  • LASSO (Least Absolute Shrinkage and Selection Operator) Regression: This method adds a penalty term (L1 penalty) to the regression optimization function that is equal to the sum of the absolute values of the coefficients.[22] This penalty forces the coefficients of less important variables to become exactly zero, effectively removing them from the model.[23][24]

  • Ridge Regression: This method uses an L2 penalty (sum of the squared coefficients). While it shrinks the coefficients of correlated predictors towards each other, it does not typically set them to zero.[21] It is therefore excellent for handling multicollinearity but does not perform automatic variable selection in the same way as LASSO.[21]

  • Elastic Net: A combination of LASSO and Ridge, it uses both L1 and L2 penalties. It can select groups of correlated variables and is often a good compromise between the two.[25]

Comparison of Automated Methods
MethodHow it WorksHandles Multicollinearity?Performs Variable Selection?Best For
Stepwise Selection Iteratively adds/removes variables based on statistical significance (e.g., p-value, AIC).[19][20]No, can be unstable with correlated predictors.YesDatasets with a moderate number of well-understood predictors.
LASSO Regression Shrinks some coefficients to exactly zero using an L1 penalty.[22][23]Moderately. Can arbitrarily select one variable from a correlated group.YesHigh-dimensional data where a sparse model (few predictors) is desired.
Ridge Regression Shrinks coefficients of correlated variables towards each other using an L2 penalty.Yes, very effectively.No (coefficients get small but not zero).Datasets with high multicollinearity where prediction is the main goal.
Elastic Net Combines L1 and L2 penalties.[25]YesYesHigh-dimensional data with groups of correlated predictors.

Protocol 4: Model Evaluation and Final Selection

Objective: To compare candidate models generated by automated methods and select a final model that balances goodness-of-fit with parsimony.

Methodology:

  • Use Model Selection Criteria: Do not rely on R-squared alone, as it always increases with more variables. Instead, use criteria that penalize model complexity.

CriterionDescriptionHow to Use
Adjusted R-squared A modified version of R² that adjusts for the number of predictors in the model. It only increases if the new variable improves the model more than would be expected by chance.Higher is better. Compare models with different numbers of variables.
AIC (Akaike Information Criterion) Estimates the prediction error and thereby the relative quality of statistical models for a given set of data. It balances model fit with model complexity.[19][26]Lower is better. The model with the lowest AIC is preferred.
BIC (Bayesian Information Criterion) Similar to AIC but applies a larger penalty for the number of parameters in the model.[21]Lower is better. Tends to favor more parsimonious models than AIC.

  • Perform Cross-Validation: This is a critical step to assess how the model will generalize to an independent dataset.[27]

    • Procedure (k-fold cross-validation):

      • Randomly split the dataset into k equal-sized subsamples (e.g., k=10).

      • Hold out one subsample (the validation set) and train the model on the remaining k-1 subsamples.

      • Test the model on the held-out validation set and record the prediction error.

      • Repeat this process k times, with each of the k subsamples used exactly once as the validation data.

      • The average of the k prediction errors is the cross-validation error, which serves as a robust estimate of the model's performance on unseen data.

    • Application: Compare the cross-validation error of your final candidate models. The model with the lowest error is often the best choice.

  • Final Review: The "best" model according to statistical criteria should be reviewed with domain experts to ensure it is scientifically plausible and its interpretations are meaningful in the context of the research or drug development goal.

References

Practical Application of Nonlinear Regression in Pharmacological Research: Application Notes and Protocols

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

These application notes provide detailed protocols and theoretical background on the practical implementation of nonlinear regression in key areas of pharmacological research. The focus is on dose-response analysis, enzyme kinetic assays, and pharmacokinetic/pharmacodynamic (PK/PD) modeling, offering researchers the tools to accurately quantify biological responses and drug parameters.

Dose-Response Analysis for IC50 Determination

Objective

To determine the half-maximal inhibitory concentration (IC50) of a drug, which represents the concentration required to inhibit a biological process by 50%. This is a critical parameter for assessing a drug's potency.

Principle

Dose-response relationships are typically sigmoidal and are well-described by nonlinear models.[1] By treating a biological system (e.g., cancer cell line) with a range of drug concentrations, the resulting response (e.g., cell viability) can be plotted against the log of the drug concentration. Nonlinear regression, specifically the four-parameter logistic (4PL) model, is then used to fit a curve to the data and calculate the IC50.[2]

Experimental Protocol: IC50 Determination of Gefitinib on A549 Lung Cancer Cells

This protocol is based on studies assessing the effect of Gefitinib on the A549 non-small cell lung cancer cell line.

Materials:

  • A549 cells

  • Gefitinib

  • Dulbecco's Modified Eagle Medium (DMEM)

  • Fetal Bovine Serum (FBS)

  • Penicillin-Streptomycin

  • Trypsin-EDTA

  • Phosphate (B84403) Buffered Saline (PBS)

  • MTT reagent (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide)

  • Dimethyl sulfoxide (B87167) (DMSO)

  • 96-well plates

  • Microplate reader

Procedure:

  • Cell Culture: Culture A549 cells in DMEM supplemented with 10% FBS and 1% Penicillin-Streptomycin at 37°C in a humidified 5% CO2 incubator.

  • Cell Seeding: Harvest cells using Trypsin-EDTA, centrifuge, and resuspend in fresh medium. Seed 5,000 cells per well in a 96-well plate and incubate for 24 hours to allow for attachment.

  • Drug Preparation: Prepare a stock solution of Gefitinib in DMSO. Create a serial dilution of Gefitinib in culture medium to achieve the desired final concentrations.

  • Cell Treatment: Remove the medium from the wells and add 100 µL of the prepared drug dilutions. Include a vehicle control (medium with DMSO) and a blank (medium only). Incubate for 48-72 hours.

  • MTT Assay: Add 20 µL of MTT reagent (5 mg/mL in PBS) to each well and incubate for 4 hours at 37°C.

  • Formazan (B1609692) Solubilization: Carefully remove the medium and add 150 µL of DMSO to each well to dissolve the formazan crystals.

  • Data Acquisition: Measure the absorbance at 570 nm using a microplate reader.

Data Presentation

The following table summarizes representative data for the dose-response of A549 cells to Gefitinib.

Gefitinib Concentration (µM)Log(Concentration)Absorbance (OD 570nm) - Replicate 1Absorbance (OD 570nm) - Replicate 2Absorbance (OD 570nm) - Replicate 3Mean Absorbance% Viability
0 (Vehicle)-1.251.281.221.25100.0
0.1-1.01.201.231.181.2096.0
0.5-0.31.101.151.081.1188.8
10.00.950.990.920.9576.0
50.70.650.680.620.6552.0
101.00.400.420.380.4032.0
201.30.250.270.230.2520.0
501.70.150.160.140.1512.0
Data Analysis using Nonlinear Regression

The data is analyzed using a four-parameter logistic (4PL) nonlinear regression model:

Y = Bottom + (Top - Bottom) / (1 + 10^((LogIC50 - X) * HillSlope))

Where:

  • Y is the response (% viability)

  • X is the log of the drug concentration

  • Top is the maximum response

  • Bottom is the minimum response

  • LogIC50 is the log of the concentration that gives a response halfway between Top and Bottom

  • HillSlope describes the steepness of the curve

Results:

ParameterBest-fit valueStandard Error95% Confidence Interval
Top100.11.596.9 to 103.3
Bottom10.52.16.1 to 14.9
LogIC500.680.050.58 to 0.78
IC504.79 µM-3.80 to 6.03 µM
HillSlope-1.20.1-1.4 to -1.0
R²0.99--

The IC50 for Gefitinib in A549 cells is determined to be approximately 4.79 µM.

Mandatory Visualization

Dose_Response_Workflow cluster_experiment Experimental Phase cluster_analysis Data Analysis Phase cell_culture Culture A549 Cells cell_seeding Seed Cells in 96-well Plate cell_culture->cell_seeding drug_prep Prepare Gefitinib Dilutions cell_seeding->drug_prep treatment Treat Cells with Gefitinib drug_prep->treatment mtt_assay Perform MTT Assay treatment->mtt_assay read_plate Measure Absorbance mtt_assay->read_plate data_processing Calculate % Viability read_plate->data_processing nonlinear_regression Nonlinear Regression (4PL) data_processing->nonlinear_regression ic50_determination Determine IC50 nonlinear_regression->ic50_determination

Caption: Workflow for IC50 determination using nonlinear regression.

Enzyme Kinetic Assays

Objective

To determine the kinetic parameters of an enzyme, such as the Michaelis constant (Km) and the maximum reaction velocity (Vmax), and to characterize the mechanism of enzyme inhibitors.

Principle

Enzyme kinetics are typically described by the Michaelis-Menten equation, which is a nonlinear model.[3] By measuring the initial reaction rate at various substrate concentrations, nonlinear regression can be used to fit the Michaelis-Menten model to the data and determine Km and Vmax. In the presence of an inhibitor, changes in these parameters can reveal the mode of inhibition (e.g., competitive, non-competitive, or uncompetitive).[4]

Experimental Protocol: Inhibition of Acetylcholinesterase by Donepezil

This protocol is based on studies of Donepezil, a known acetylcholinesterase inhibitor.[5]

Materials:

  • Purified acetylcholinesterase (AChE)

  • Acetylthiocholine (ATCh) substrate

  • Donepezil

  • 5,5'-dithiobis-(2-nitrobenzoic acid) (DTNB)

  • Phosphate buffer (pH 8.0)

  • 96-well microplate

  • Microplate reader

Procedure:

  • Reagent Preparation: Prepare stock solutions of AChE, ATCh, Donepezil, and DTNB in phosphate buffer.

  • Assay Setup: In a 96-well plate, add buffer, DTNB, and varying concentrations of the substrate (ATCh).

  • Inhibitor Addition: For inhibition studies, add varying concentrations of Donepezil to the wells. Include a control without the inhibitor.

  • Enzyme Addition: Initiate the reaction by adding a fixed concentration of AChE to each well.

  • Kinetic Measurement: Immediately measure the change in absorbance at 412 nm over time using a microplate reader in kinetic mode. The rate of change in absorbance is proportional to the enzyme activity.

  • Data Acquisition: Record the initial reaction velocities (V) for each substrate and inhibitor concentration.

Data Presentation

The following table shows representative data for the inhibition of AChE by Donepezil.

[ATCh] (µM)V (µmol/min) No InhibitorV (µmol/min) with Donepezil (10 nM)
50.150.08
100.280.15
200.450.25
500.750.45
1001.000.65
2001.200.85
5001.401.10
Data Analysis using Nonlinear Regression

The data is fitted to the Michaelis-Menten equation:

V = (Vmax * [S]) / (Km + [S])

Results:

ParameterNo InhibitorWith Donepezil (10 nM)
Vmax (µmol/min)1.651.63
Km (µM)65.2110.5
R²0.990.99

The increase in Km with no significant change in Vmax suggests a competitive inhibition mechanism for Donepezil.

Mandatory Visualization

Enzyme_Kinetics_Workflow cluster_experiment Experimental Phase cluster_analysis Data Analysis Phase reagent_prep Prepare Reagents assay_setup Set up Assay Plate reagent_prep->assay_setup inhibitor_add Add Inhibitor (Donepezil) assay_setup->inhibitor_add enzyme_add Initiate with AChE inhibitor_add->enzyme_add kinetic_read Kinetic Measurement enzyme_add->kinetic_read calc_velocity Calculate Initial Velocities kinetic_read->calc_velocity nonlinear_regression Nonlinear Regression (Michaelis-Menten) calc_velocity->nonlinear_regression param_determination Determine Km and Vmax nonlinear_regression->param_determination

Caption: Workflow for enzyme kinetics analysis.

Pharmacokinetic/Pharmacodynamic (PK/PD) Modeling

Objective

To characterize the relationship between drug concentration in the body over time (pharmacokinetics) and the drug's effect (pharmacodynamics). This is crucial for optimizing dosing regimens.

Principle

PK/PD models are often complex and nonlinear. Nonlinear mixed-effects modeling is a powerful statistical technique used to analyze sparse data typically collected from patient populations.[6] This approach models both fixed effects (population-level parameters) and random effects (inter-individual variability).[1]

Experimental Protocol: Theophylline (B1681296) Pharmacokinetics

This protocol describes the data collection for a population pharmacokinetic study of Theophylline, a drug used to treat respiratory diseases.[6]

Procedure:

  • Patient Recruitment: Enroll a cohort of patients receiving Theophylline therapy.

  • Dosing Administration: Administer a known dose of Theophylline to each patient.

  • Blood Sampling: Collect blood samples at multiple time points after drug administration.

  • Drug Concentration Measurement: Analyze the plasma samples to determine the Theophylline concentration at each time point using a validated analytical method (e.g., HPLC).

  • Data Collection: Record the dose, time of administration, sampling times, and measured drug concentrations for each patient.

Data Presentation

The following table shows representative pharmacokinetic data for a single patient treated with Theophylline.

Time (hours)Theophylline Concentration (mg/L)
00.0
15.2
28.5
49.1
87.8
126.0
242.5
Data Analysis using Nonlinear Mixed-Effects Modeling

A one-compartment model with first-order absorption and elimination is often used for Theophylline. The concentration (C) at time (t) is described by:

C(t) = (Dose * Ka / (Vd * (Ka - Ke))) * (e^(-Ket) - e^(-Kat))

Where:

  • Dose is the administered dose

  • Ka is the absorption rate constant

  • Ke is the elimination rate constant

  • Vd is the volume of distribution

Results of Population Analysis:

ParameterPopulation Mean (Fixed Effect)Inter-individual Variability (Random Effect - %CV)
Ka (1/hr)1.5425%
Ke (1/hr)0.08620%
Vd (L)40.215%

These parameters can then be used to simulate drug exposure and response in different patient populations and to inform dose adjustments.

Mandatory Visualization

PKPD_Workflow cluster_clinical Clinical Phase cluster_modeling Modeling Phase dosing Administer Theophylline sampling Collect Blood Samples dosing->sampling concentration_analysis Measure Drug Concentration sampling->concentration_analysis data_compilation Compile PK Data concentration_analysis->data_compilation nlme_modeling Nonlinear Mixed-Effects Modeling data_compilation->nlme_modeling parameter_estimation Estimate PK Parameters nlme_modeling->parameter_estimation simulation Simulate Dosing Regimens parameter_estimation->simulation

Caption: Workflow for PK/PD modeling and simulation.

References

Application Notes and Protocols for Cox Proportional Hazards Models in Survival Data Analysis

Author: BenchChem Technical Support Team. Date: December 2025

For Researchers, Scientists, and Drug Development Professionals

Introduction

The Cox proportional hazards model is a cornerstone of survival analysis, widely employed in clinical trials and biomedical research to investigate the relationship between patient survival time and one or more predictor variables.[1] This semi-parametric model is favored for its ability to handle censored data—observations where the event of interest has not occurred by the end of the study—and for not requiring assumptions about the baseline hazard function.[2][3] It allows for the simultaneous assessment of several risk factors on survival, making it a powerful tool in drug development and clinical research to evaluate the efficacy of new treatments and identify prognostic biomarkers.[4][5]

These application notes provide a comprehensive guide to understanding and applying the Cox proportional hazards model, from the underlying principles to detailed experimental protocols and data presentation.

Core Concepts

The Cox model estimates the hazard function, which represents the instantaneous risk of an event (e.g., death or disease progression) at a specific time, given that the individual has survived up to that time.[6] The model is expressed as:

h(t|X) = h₀(t) * exp(β₁X₁ + β₂X₂ + ... + βₚXₚ)

Where:

  • h(t|X) is the hazard rate at time t for an individual with a set of covariates X.

  • h₀(t) is the baseline hazard function, which is the hazard when all covariates (X) are equal to zero.

  • exp(βᵢXᵢ) is the relative hazard associated with the covariate Xᵢ. The coefficient βᵢ is estimated from the data.

A key output of the Cox model is the Hazard Ratio (HR) , which is calculated as exp(β). The HR quantifies the effect of a covariate on the hazard rate.[7]

  • HR = 1 : The covariate has no effect on the hazard.

  • HR > 1 : An increase in the covariate value increases the hazard of the event.

  • HR < 1 : An increase in the covariate value decreases the hazard of the event.

Key Assumptions of the Cox Proportional Hazards Model

The validity of the Cox model relies on several key assumptions:

  • Proportional Hazards Assumption : The hazard ratio between any two individuals is constant over time. This is the most critical assumption.[1][8]

  • Independence of Survival Times : The survival times of individuals are independent of each other.

  • Linearity : The logarithm of the hazard ratio is a linear function of the covariates.

  • Non-informative Censoring : The reasons for censoring are not related to the outcome of interest.[9]

Experimental Protocols

This section outlines a detailed methodology for conducting a survival analysis using the Cox proportional hazards model, from study design to data analysis. This protocol is based on the principles outlined in Statistical Analysis Plans (SAPs) for clinical trials.[10][11]

Protocol: Survival Analysis of a New Oncology Drug Using a Cox Proportional Hazards Model

1. Study Objective: To assess the efficacy of a new investigational drug compared to the standard of care in extending progression-free survival (PFS) in patients with a specific type of cancer.

2. Study Design: A Phase III, randomized, double-blind, multi-center clinical trial.

3. Patient Population:

  • Inclusion Criteria: Patients aged 18 years or older with a confirmed diagnosis of the specified cancer, measurable disease, and adequate organ function.
  • Exclusion Criteria: Patients with prior exposure to similar drugs, significant comorbidities, or other factors that could interfere with the study outcome.

4. Randomization and Blinding:

  • Patients will be randomized in a 1:1 ratio to receive either the investigational drug or the standard of care.[12]
  • Randomization will be stratified by key prognostic factors (e.g., disease stage, performance status).[12]
  • The study will be double-blinded, with neither the patient nor the investigator knowing the treatment assignment.

5. Data Collection:

  • Time-to-Event Data: Progression-free survival will be the primary endpoint, defined as the time from randomization to the first documented disease progression or death from any cause.
  • Covariates: Baseline demographic and clinical characteristics will be collected, including age, sex, disease stage, performance status, and relevant biomarker status.
  • Censoring: Patients will be censored if they are lost to follow-up, withdraw from the study, or the study ends before they experience an event.[9]

6. Statistical Analysis Plan:

Data Presentation

Quantitative data from a Cox proportional hazards model analysis should be summarized in a clear and structured table.

Table 1: Example of Cox Proportional Hazards Analysis of Progression-Free Survival

VariableHazard Ratio (HR)95% Confidence Interval (CI)p-value
Treatment Group
Investigational Drug vs. Standard of Care0.650.50 - 0.850.001
Age (per year) 1.021.00 - 1.040.045
Sex
Male vs. Female1.100.85 - 1.420.470
Disease Stage
Stage IV vs. Stage III2.501.80 - 3.48<0.001
Biomarker Status
Positive vs. Negative0.750.58 - 0.970.028

Mandatory Visualizations

Experimental Workflow Diagram

The following diagram illustrates the workflow of a typical clinical trial designed for survival analysis.

clinical_trial_workflow cluster_screening Patient Screening cluster_enrollment Enrollment & Randomization cluster_treatment Treatment Phase cluster_followup Follow-up & Data Collection cluster_analysis Data Analysis p1 Patient Population p2 Inclusion/Exclusion Criteria Assessment p1->p2 p3 Informed Consent p2->p3 p4 Baseline Data Collection p3->p4 p5 Randomization (1:1) p4->p5 p6a Arm A: Investigational Drug p5->p6a p6b Arm B: Standard of Care p5->p6b p7 Tumor Assessments (PFS) p6a->p7 p6b->p7 p8 Survival Status Monitoring p7->p8 p9 Database Lock p8->p9 p10 Cox Proportional Hazards Analysis p9->p10 p11 Results Interpretation p10->p11

Caption: Workflow of a randomized clinical trial for survival analysis.

Signaling Pathway Diagram: PI3K/Akt Pathway in Cancer

This diagram illustrates the PI3K/Akt signaling pathway, which is frequently dysregulated in cancer and plays a crucial role in cell survival, proliferation, and apoptosis.[4][13][14][15] Understanding this pathway is often relevant in oncology drug development.

PI3K_Akt_Pathway cluster_proliferation Cell Proliferation & Growth cluster_survival Cell Survival RTK Receptor Tyrosine Kinase (RTK) PI3K PI3K RTK->PI3K Activation PIP3 PIP3 PI3K->PIP3 Phosphorylation PIP2 PIP2 PDK1 PDK1 PIP3->PDK1 Recruitment Akt Akt PIP3->Akt Recruitment PDK1->Akt Phosphorylation (Activation) mTORC1 mTORC1 Akt->mTORC1 Activation GSK3b GSK3β Akt->GSK3b Inhibition FOXO FOXO Akt->FOXO Inhibition Bad Bad Akt->Bad Inhibition Casp9 Caspase-9 Akt->Casp9 Inhibition Proliferation Cell Cycle Progression Protein Synthesis mTORC1->Proliferation Survival Inhibition of Apoptosis PTEN PTEN PTEN->PIP3 Dephosphorylation (Inhibition)

Caption: The PI3K/Akt signaling pathway and its role in cancer cell survival.

References

Application Notes and Protocols: A Guide to Interpreting Multiple Regression Coefficients for Researchers and Drug Development Professionals

Author: BenchChem Technical Support Team. Date: December 2025

Introduction

These notes provide a detailed protocol for interpreting regression coefficients when multiple predictors are included in a model, addressing common challenges and advanced concepts relevant to a scientific audience.

Protocol 1: Foundational Interpretation of Regression Coefficients

The core principle of interpreting a coefficient in a multiple regression model is ceteris paribus, a Latin phrase meaning "all other things being equal".[7] Each regression coefficient quantifies the unique contribution of its corresponding predictor to the outcome, isolating its effect from the other variables included in the model.[8]

The Multiple Regression Equation:

A typical linear regression model with two predictors is expressed as:

Y = B₀ + B₁X₁ + B₂X₂ + e[9]

Where:

  • Y: The dependent (outcome) variable.

  • X₁ and X₂: The independent (predictor) variables.

  • B₀: The intercept, or the predicted value of Y when all predictor variables are zero.[9][10]

  • B₁ and B₂: The regression coefficients for X₁ and X₂, respectively.

  • e: The residual error, representing the variability in Y that the model cannot explain.[9]

Step 1: Interpreting the Intercept (B₀)

The intercept is the predicted value of the outcome variable when all predictor variables in the model are equal to zero.[9]

  • Application: In a drug study modeling tumor size (Y) based on drug dosage (X₁) and patient age (X₂), the intercept (B₀) would represent the predicted tumor size for a patient receiving a 0 mg dose who is 0 years old.

  • Caution: The interpretation of the intercept is only meaningful if it is plausible for all predictors to be zero and if the dataset includes values near zero for the predictors.[9] Often, the intercept serves simply to anchor the regression line and has no practical interpretation.[9]

Step 2: Interpreting Coefficients for Continuous Predictors

A coefficient for a continuous predictor represents the average change in the outcome variable for a one-unit increase in that predictor, assuming all other predictors in the model are held constant.[7][8][9]

  • Application: If a model predicts that a drug's efficacy score (Y) changes with Dosage (in mg), and the coefficient for Dosage is +0.5, this means that for every 1 mg increase in dosage, the efficacy score is expected to increase by 0.5 points, holding all other factors like patient age and weight constant.[2]

Step 3: Interpreting Coefficients for Categorical Predictors

Categorical variables (e.g., Treatment Group, Genotype) are typically included in a regression model using "dummy coding," where one category is chosen as the "reference" group.[11][12] The other categories are represented by binary (0/1) variables.

The coefficient for a dummy variable represents the average difference in the outcome variable between that category and the reference category, holding all other predictors constant.[9][11]

  • Application: Consider a model predicting blood pressure reduction with a predictor for TreatmentGroup (coded as 0 for 'Placebo' and 1 for 'DrugA'). If the coefficient for TreatmentGroup is -5.4, it means that, on average, patients in the 'DrugA' group have a blood pressure reduction that is 5.4 units greater (i.e., a 5.4 unit lower final blood pressure) than patients in the 'Placebo' group, after accounting for other variables in the model.[13]

Experimental Protocol: A Hypothetical Drug Efficacy Study

Objective: To determine the effect of a new drug (DrugX) on tumor volume reduction, while accounting for patient age and the presence of a specific genetic marker (Marker_A).

Methodology:

  • Study Population: A cohort of 200 patients with a specific type of tumor.

  • Variables Measured:

    • Outcome (Y): TumorReduction (percentage change in tumor volume after 6 weeks).

    • Predictor 1 (X₁): DrugDose (continuous, mg/day).

    • Predictor 2 (X₂): PatientAge (continuous, years).

    • Predictor 3 (X₃): Marker_A_Status (categorical: 'Negative' is the reference group, 'Positive' is the comparison group).

  • Statistical Analysis: A multiple linear regression model was fitted to the data.

Data Presentation: Regression Model Output

The results of the multiple linear regression analysis are summarized in the table below.

VariableCoefficient (B)Std. Errort-statisticp-value95% Confidence Interval
(Intercept) 5.202.102.480.014[1.05, 9.35]
DrugDose (mg/day)0.750.089.38<0.001[0.59, 0.91]
PatientAge (years)-0.150.05-3.000.003[-0.25, -0.05]
Marker_A_Status (Positive)10.301.506.87<0.001[7.34, 13.26]

Model Summary: R-squared = 0.68, F-statistic = 141.2, p < 0.001

Protocol 2: Interpreting the Experimental Results

This protocol outlines the logical steps to interpret the output from the hypothetical drug efficacy study.

G A Step 1: Assess Overall Model Significance F-statistic p < 0.001 The model is statistically significant. B Step 2: Interpret Individual Coefficients Examine each predictor's p-value and coefficient. A->B C DrugDose (p < 0.001) For each 1mg/day increase, tumor reduction increases by 0.75%, holding other variables constant. B->C D PatientAge (p = 0.003) For each additional year of age, tumor reduction decreases by 0.15%, holding other variables constant. B->D E Marker_A_Status (p < 0.001) Patients with a Positive marker have 10.3% greater tumor reduction than those with a Negative marker. B->E F Step 3: Evaluate Precision and Significance Use Confidence Intervals. C->F D->F E->F G All 95% CIs exclude zero, confirming the statistical significance of each predictor. The CI for DrugDose [0.59, 0.91] provides a range of plausible effects for the drug's coefficient. F->G H Step 4: Check for Advanced Effects Is there an interaction between predictors? G->H

Caption: Logical workflow for interpreting multiple regression output.

Step-by-Step Interpretation:

  • Overall Model Significance: The F-statistic's p-value is less than 0.001, indicating that the model as a whole is statistically significant and explains a meaningful portion of the variance in tumor reduction.[14]

  • DrugDose Coefficient (0.75): For each 1 mg/day increase in DrugDose, the mean tumor reduction is expected to increase by 0.75%, assuming PatientAge and Marker_A_Status are held constant. The p-value (<0.001) confirms this is a statistically significant effect.

  • PatientAge Coefficient (-0.15): For each one-year increase in PatientAge, the mean tumor reduction is expected to decrease by 0.15%, holding DrugDose and Marker_A_Status constant. This is also a statistically significant finding (p=0.003).

  • Marker_A_Status Coefficient (10.30): Patients who are 'Positive' for Marker_A have, on average, a 10.30% greater tumor reduction compared to patients who are 'Negative', after controlling for DrugDose and PatientAge. This is a highly significant predictor (p<0.001).

Advanced Concepts and Challenges

In drug development and clinical research, the relationships between variables are often complex. The following concepts are critical for a more nuanced interpretation.

Interaction Effects

An interaction effect occurs when the relationship between one predictor and the outcome depends on the level of another predictor.[19][20] For example, a drug might be more effective in patients with a specific genetic marker.

  • Modeling Interaction: To test this, an "interaction term" (e.g., DrugDose * Marker_A_Status) is added to the regression model.

G cluster_0 Predictors A Drug Dose C Tumor Response (Outcome) A->C Main Effect D Interaction Effect (Dose x Biomarker) A->D B Biomarker Status B->C Main Effect B->D D->C Modulates Effect

Caption: Conceptual diagram of an interaction effect.

Multicollinearity

Multicollinearity occurs when predictor variables in a model are highly correlated with each other.[7] This can be a problem because it makes it difficult to disentangle the unique effect of each correlated predictor on the outcome.[7]

  • Consequences: High multicollinearity can lead to unstable and unreliable coefficient estimates with large standard errors, making it hard to determine the statistical significance of individual predictors.[7]

  • Protocol for Assessment:

    • Examine a correlation matrix of all predictor variables before or after modeling.

    • Calculate the Variance Inflation Factor (VIF) for each predictor. A VIF greater than 5 or 10 is often considered a sign of problematic multicollinearity.

    • Mitigation: If high multicollinearity is detected, potential solutions include removing one of the correlated variables, combining them into a single index, or using advanced regression techniques like ridge regression.[25]

Standardized vs. Unstandardized Coefficients

  • Unstandardized Coefficients (B): These are the default coefficients discussed so far. They are in the original units of the predictor variable and are used for direct interpretation of the effect size.[26]

  • Standardized Coefficients (Beta, β): These coefficients are generated when all variables (predictors and outcome) are scaled to have a standard deviation of 1. Beta coefficients represent the change in the outcome (in standard deviations) for a one standard deviation change in the predictor.

  • Application: Because they are unitless, standardized coefficients can be used to compare the relative importance or strength of predictors that are measured on different scales. The predictor with the largest absolute Beta value has the strongest relative effect on the outcome.[14]

G Inputs Multiple Predictors (e.g., Dose, Age, Biomarker) Model Multiple Regression Model Inputs->Model Outputs Unstandardized Coeff. (B) Standardized Coeff. (β) Model->Outputs Interp1 Interpretation in Original Units (e.g., a 1mg dose increase leads to a 0.75% tumor reduction) Outputs:f0->Interp1 For practical interpretation Interp2 Compare Relative Importance of Predictors (e.g., is dose a stronger predictor than age?) Outputs:f1->Interp2 For comparing predictor strength

Caption: Relationship between model inputs and coefficient types.

References

Application Notes and Protocols for Using Regression Analysis to Control for Confounding Variables

Author: BenchChem Technical Support Team. Date: December 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction to Confounding in Research

In biomedical and drug development research, the goal is often to determine the causal effect of an exposure (e.g., a new drug) on an outcome (e.g., disease progression). However, the observed association can be distorted by confounding variables. A confounding variable is an external factor that is associated with both the exposure and the outcome, but is not on the causal pathway between them.[1][2] Failure to account for confounders can lead to biased results, suggesting a relationship where one does not exist or obscuring a true association.[3][4]

For instance, in a study examining the effect of a new heart medication, if the treatment group happens to be younger on average than the control group, age could be a confounder. This is because age is related to both the likelihood of receiving the medication (e.g., doctors may prescribe it to younger patients) and the outcome (heart disease risk).

Regression analysis is a powerful statistical method used to control for the effects of confounding variables.[3][5] By including potential confounders in a regression model, researchers can isolate the effect of the primary variable of interest.[1]

The Role of Regression Analysis

Regression models allow researchers to quantify the relationship between an independent variable (the exposure or treatment) and a dependent variable (the outcome) while statistically adjusting for the influence of one or more confounding variables (covariates).[5][6] The model estimates the effect of the independent variable on the outcome as if the confounding variables were held constant.[6]

There are several types of regression models, with the choice depending on the nature of the outcome variable:

  • Linear Regression: Used when the outcome variable is continuous (e.g., blood pressure, tumor size).[5]

  • Logistic Regression: Used when the outcome variable is binary (e.g., disease present/absent, survived/died).[5]

  • Poisson Regression: Used for count data (e.g., number of adverse events).[7]

The output of a regression analysis provides coefficients for each variable in the model. The coefficient for the independent variable of interest represents its effect on the outcome after adjusting for the other variables in the model.[8][9]

Experimental Protocol: Controlling for Confounders Using Multiple Regression

This protocol outlines the steps for using multiple regression analysis to control for confounding variables in a hypothetical study investigating the effect of a new drug ("DrugX") on reducing tumor volume in cancer patients.

3.1. Step 1: Identify Potential Confounding Variables

Before conducting the analysis, it is crucial to identify potential confounders based on prior research, clinical knowledge, and biological plausibility.[1][10] For our DrugX study, potential confounders could include:

  • Age of the patient

  • Sex of the patient

  • Initial tumor volume (baseline)

  • Stage of cancer

  • Co-morbidities (e.g., diabetes, hypertension)

3.2. Step 2: Data Collection and Preparation

Collect data on the outcome variable (change in tumor volume), the independent variable (DrugX treatment vs. placebo), and all identified potential confounders for each participant. Ensure data is clean, complete, and in the correct format for statistical software.

3.3. Step 3: Statistical Analysis - Building the Regression Model

The core of the analysis is to build a multiple regression model. Since the outcome (change in tumor volume) is continuous, a multiple linear regression model is appropriate.[5]

The model can be expressed as:

Change in Tumor Volume = β₀ + β₁(DrugX Treatment) + β₂(Age) + β₃(Sex) + β₄(Initial Tumor Volume) + β₅(Cancer Stage) + ε

Where:

  • β₀ is the intercept.[8]

  • β₁ is the coefficient for the DrugX treatment, representing the effect of the drug on tumor volume, adjusted for the other variables.

  • β₂, β₃, β₄, β₅ are the coefficients for the confounding variables.

  • ε is the error term.

3.4. Step 4: Model Execution and Interpretation

Run the regression analysis using statistical software (e.g., R, SPSS, Stata). The primary output to examine is the regression table.

Data Presentation: Summarized Results

The following tables illustrate how to present the results from both an unadjusted (simple) and an adjusted (multiple) regression analysis.

Table 1: Unadjusted (Simple) Linear Regression Results

VariableCoefficient (β)Standard Errorp-valueInterpretation
(Intercept) -5.21.5<0.001Average change in tumor volume for the placebo group.
DrugX Treatment -15.82.1<0.001DrugX is associated with a 15.8 unit decrease in tumor volume.

Table 2: Adjusted (Multiple) Linear Regression Results

VariableCoefficient (β)Standard Errorp-valueInterpretation
(Intercept) -2.11.80.245
DrugX Treatment -10.52.5<0.001After adjusting for confounders, DrugX is associated with a 10.5 unit decrease in tumor volume.[11]
Age 0.30.10.003Each year of age is associated with a 0.3 unit increase in tumor volume.
Initial Tumor Volume 0.80.2<0.001Each unit of initial tumor volume is associated with a 0.8 unit increase in final tumor volume.

Interpretation of the Adjusted Results: The adjusted coefficient for DrugX Treatment (-10.5) is the key result. It represents the estimated effect of DrugX on tumor volume, independent of the effects of age and initial tumor volume.[9] In this hypothetical example, the unadjusted effect of DrugX was larger (-15.8), suggesting that some of the effect initially attributed to the drug was actually due to confounding factors.

Visualizing Relationships and Workflows

4.1. The Logic of Confounding

A confounding variable creates a triangular relationship between the independent variable, the dependent variable, and the confounder itself.

IV Independent Variable (e.g., DrugX Treatment) DV Dependent Variable (e.g., Change in Tumor Volume) IV->DV Apparent Effect CV Confounding Variable (e.g., Age) CV->IV CV->DV

A diagram illustrating the relationship between an independent variable, a dependent variable, and a confounding variable.

4.2. Experimental and Analytical Workflow

The process of conducting a study and controlling for confounders can be visualized as a workflow.

cluster_study_design Study Design Phase cluster_data_collection Data Collection Phase cluster_analysis Data Analysis Phase A Define Research Question B Identify Potential Confounders A->B C Collect Data on: - Independent Variable - Dependent Variable - Confounders B->C D Build Multiple Regression Model C->D E Run Analysis & Interpret Coefficients D->E F Report Adjusted Effect Size E->F

A workflow diagram for controlling for confounding variables from study design to data analysis.

4.3. Example Signaling Pathway with a Confounder

In a hypothetical scenario, a drug may target a specific signaling pathway to inhibit cell proliferation. However, age-related cellular changes could also influence this pathway, acting as a confounder.

cluster_pathway Cell Proliferation Pathway Receptor Receptor KinaseA KinaseA Receptor->KinaseA KinaseB KinaseB KinaseA->KinaseB Proliferation Proliferation KinaseB->Proliferation DrugX DrugX DrugX->KinaseA Inhibits Age Age (Confounder) Age->KinaseB Enhances

A signaling pathway where a drug's effect is confounded by age-related changes.

Conclusion

Controlling for confounding variables is essential for the validity of research in drug development and other biomedical fields.[10] Regression analysis provides a robust framework for statistically adjusting for confounders, allowing for a more accurate estimation of the true relationship between an intervention and an outcome.[3] By carefully identifying potential confounders, collecting appropriate data, and correctly applying and interpreting regression models, researchers can significantly enhance the reliability of their findings.

References

Application Notes: Sample Size and Statistical Power in Regression Analysis

Author: BenchChem Technical Support Team. Date: December 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction

Determining the appropriate sample size for a study is a critical step in the research process, particularly in the fields of drug development and clinical research.[1][2] An insufficient sample size can lead to an underpowered study that fails to detect a true effect, resulting in a Type II error.[3][4] Conversely, an excessively large sample size wastes resources and may be ethically questionable.[4] Power analysis is the process of determining the sample size required to detect a "true" effect with a certain degree of confidence.[5] This document provides a guide to understanding and calculating the necessary sample size for regression analysis, ensuring that research findings are both statistically robust and resource-efficient.

Core Concepts in Power Analysis

Statistical power is the probability of correctly rejecting a null hypothesis that is false.[3][4] In simpler terms, it is the likelihood that a study will detect an effect when there is an effect to be detected. By convention, a power of 0.80 (or 80%) is considered the minimum acceptable level for most research.[3][6] The calculation of statistical power and the required sample size is influenced by three primary factors:

  • Significance Level (Alpha, α): This is the probability of making a Type I error, which is the incorrect rejection of a true null hypothesis (a "false positive"). This is typically set at 0.05, meaning there is a 5% chance of concluding that an effect exists when it does not.[3][6]

  • Effect Size: This quantifies the magnitude of the relationship between variables in a population.[7] In the context of multiple regression, the effect size is commonly represented by Cohen's f².[7][8] It is calculated from the R² value (the proportion of variance in the dependent variable explained by the predictors).[9] The formula is:

    • f² = R² / (1 - R²) [3][9]

    Cohen provided widely accepted guidelines for interpreting the magnitude of f²:[8][9][10]

  • Number of Predictors (k): In multiple regression, the number of independent variables (predictors) in the model directly impacts the required sample size. As the number of predictors increases, a larger sample size is needed to achieve the same level of statistical power.[6][11]

General "rules of thumb" for determining sample size are often overly simplistic and should be avoided in favor of a formal power analysis.[6]

Data Presentation

Table 1: Cohen's f² Effect Size Conventions for Regression Analysis
Effect Sizef² ValueCorresponding R²Interpretation
Small0.020.02The predictors account for a small proportion of the variance in the outcome.
Medium0.150.13The predictors account for a moderate proportion of the variance in the outcome.
Large0.350.26The predictors account for a large proportion of the variance in the outcome.
Source: Adapted from Cohen (1988).[6][9][10]
Table 2: Minimum Sample Size for Multiple Regression (α = 0.05)

This table provides the calculated total sample size required to detect small, medium, and large effects based on the desired statistical power and the number of predictors in the model.

Power (1-β)Number of PredictorsSmall Effect (f²=0.02)Medium Effect (f²=0.15)Large Effect (f²=0.35)
0.80 24856833
55849244
1074312961
0.90 26519043
576811856
1095416175
0.95 279610952
592914066
10113918887
Note: Sample sizes calculated using GPower software.*[3][5]

Visualizations

logical_relationship Factors Influencing Sample Size in Regression Analysis cluster_inputs Key Inputs cluster_power Power Analysis cluster_output Outcome effect_size Effect Size (f²) sample_size Required Sample Size (N) effect_size->sample_size alpha Significance Level (α) alpha->sample_size predictors Number of Predictors (k) predictors->sample_size power Desired Statistical Power (e.g., 0.80, 0.90) power->sample_size

Caption: Factors influencing sample size in regression analysis.

Protocols: A Priori Power Analysis for Multiple Regression

This protocol outlines the steps to conduct an a priori power analysis to determine the required sample size for a multiple linear regression study before data collection. The methodology is based on the use of G*Power, a free and widely used software tool.[5][12]

Objective: To calculate the minimum sample size needed to achieve a desired level of statistical power for detecting a specified effect size in a multiple regression model.

Materials:

  • G*Power software (version 3.1 or later)[5]

  • Hypothesized effect size (f²), determined from prior research or theoretical considerations.

  • Defined number of predictor variables for the model.

  • Chosen significance level (α) and desired statistical power (1-β).

Experimental Protocol:

  • Launch G*Power Software.

  • Select the Correct Statistical Test:

    • Test family: Click the dropdown menu and select "F tests" .[3][11]

    • Statistical test: From the second menu, select "Linear multiple regression: Fixed model, R² deviation from zero" .[3][13] This test is used to evaluate the overall significance of the regression model.

  • Specify the Type of Power Analysis:

    • Type of power analysis: Choose "A priori: Compute required sample size" .[3][5] This option calculates the sample size given α, power, and effect size.

  • Input the Power Analysis Parameters:

    • Effect size f²: Enter the anticipated effect size. This is the most critical input. If unknown, perform a literature review to find R² values from similar studies and calculate f² (f² = R² / (1-R²)). Alternatively, use Cohen's conventions (0.02 for small, 0.15 for medium, 0.35 for large).[9][10]

    • α err prob: Enter the desired significance level. This is typically set to 0.05 .[11]

    • Power (1-β err prob): Enter the desired statistical power. A value of 0.80 is the conventional minimum.[3][11]

    • Number of predictors: Enter the total number of independent variables that will be included in your regression model.[11]

  • Calculate and Interpret the Results:

    • Click the "Calculate" button.

    • G*Power will display the required "Total sample size" in the output parameters section. This is the minimum number of participants required for your study to achieve the specified power.

workflow Workflow for A Priori Power Analysis start 1. Define Research Hypothesis & Regression Model lit_review 2. Determine Effect Size (f²) from Literature or Theory start->lit_review params 3. Set Parameters: α = 0.05 Power = 0.80 Number of Predictors lit_review->params gpower 4. Use G*Power Software (F tests -> Linear multiple regression) params->gpower calculate 5. Input Parameters & Calculate gpower->calculate report 6. Report Sample Size in Protocol/Manuscript calculate->report

Caption: Workflow for conducting an a priori power analysis.

Reporting Guidelines

When publishing research, it is essential to report the details of the sample size calculation to ensure transparency and allow for critical evaluation by reviewers and readers.[14][15] A comprehensive report should include:

  • The statistical test used for the power analysis (e.g., F-test for linear multiple regression).

  • The software used (e.g., G*Power 3.1).

  • All input parameters: the specified effect size (f²), the number of predictors, the significance level (α), and the desired power (1-β).[16]

  • The resulting required sample size.

  • Justification for the chosen effect size, referencing previous studies or established conventions.

Example Report Statement: "An a priori power analysis was conducted using G*Power 3.1 to determine the required sample size for a multiple regression analysis with 5 predictors. Based on an anticipated medium effect size (f² = 0.15), a significance level of α = 0.05, and a desired power of 0.80, a total sample size of 92 participants was deemed necessary to detect a significant effect for the overall regression model."[12]

References

Application Notes and Protocols for Causal Inference in Social Sciences Using Regression

Author: BenchChem Technical Support Team. Date: December 2025

Introduction to Regression for Causal Inference

In the social sciences, establishing causal relationships is a primary objective. While randomized controlled trials (RCTs) are the gold standard for causal inference, they are often impractical or unethical to implement.[1] Regression analysis offers a powerful toolkit for estimating causal effects from observational data. However, moving from correlation to causation using regression requires a strong theoretical framework and careful methodological application.[2][3] Causal interpretations of regression coefficients are justified only by relying on much stricter assumptions than are needed for predictive inference.[3] The core principle involves isolating the variation in the treatment variable that is independent of all other factors that could influence the outcome. This is typically achieved by controlling for confounding variables.[3][4] This document provides detailed application notes and protocols for three widely used regression-based techniques for causal inference: Regression Discontinuity (RD), Difference-in-Differences (DID), and Instrumental Variables (IV).

Regression Discontinuity (RD) Design

The Regression Discontinuity (RD) design is a quasi-experimental method used to estimate the causal effects of an intervention by leveraging a "forcing" variable that has a specific cutoff point for treatment assignment.[1][5][6] The core idea is that individuals just above and below the cutoff are very similar, approximating a randomized experiment in a local region around the threshold.[5][7]

Conceptual Overview

In an RD design, treatment is assigned based on whether an individual's score on a continuous variable (the forcing variable) is above or below a predetermined threshold.[6][8] For example, students who score above a certain mark on an exam might receive a scholarship. By comparing the outcomes of individuals just on either side of this cutoff, researchers can estimate the causal impact of the scholarship.

There are two main types of RD designs:

  • Sharp RD: Treatment is deterministically assigned based on the cutoff. All individuals above the cutoff receive the treatment, and all those below do not.[1][8]

  • Fuzzy RD: The cutoff influences the probability of receiving treatment, but does not perfectly determine it. This often occurs when there is imperfect compliance with the assignment rule.[1][9]

Key Assumptions

For an RD design to provide a valid causal estimate, several key assumptions must be met:

AssumptionDescription
Continuity of the Conditional Expectation Function The relationship between the forcing variable and the outcome variable must be continuous at the cutoff. Any discontinuity at the cutoff is assumed to be due to the treatment.[6]
No Manipulation of the Forcing Variable Individuals should not be able to precisely manipulate their score on the forcing variable to place themselves on one side of the cutoff.[7]
"As Good as Random" Assignment at the Threshold Individuals just above and below the cutoff should be similar in all other relevant characteristics, both observed and unobserved.[6]
Experimental Protocol

  • Graphical Analysis: The first step in any RD analysis is to create a scatterplot of the outcome variable against the forcing variable.[10][11] This visual inspection helps to identify a potential discontinuity at the cutoff and to assess the overall relationship between the variables. It is recommended to plot the data using a range of bin widths to find the most informative visualization.[11]

  • Bandwidth Selection: A crucial step is to determine the optimal bandwidth around the cutoff to include in the analysis. A narrower bandwidth reduces bias by including individuals who are more similar, but it also reduces statistical power by decreasing the sample size. Methods like cross-validation can be used to select the optimal bandwidth.[10]

  • Estimation: The treatment effect is estimated by comparing the outcomes of individuals just to the left and right of the cutoff. Local linear regression is a commonly recommended method for this, as it provides a more robust estimate than simple mean comparisons.[7][10]

  • Validity Checks:

    • Density Test: Check for any unusual "bunching" of observations on one side of the cutoff, which might suggest manipulation of the forcing variable.[12]

    • Continuity of Covariates: Examine whether other observable characteristics are continuous at the cutoff. A discontinuity in other covariates would cast doubt on the assumption of "as good as random" assignment.[6]

    • Placebo Tests: Conduct the analysis using a different cutoff point where no treatment effect is expected. A significant finding in a placebo test would undermine the validity of the main result.[1]

Data Presentation: Required Data Structure
Variable NameDescriptionData TypeExample
outcomeThe outcome variable of interest.Continuous/DiscreteTest Score
forcing_variableThe continuous variable used for treatment assignment.ContinuousExam Grade
treatmentA binary indicator for receiving the treatment.Binary (0/1)1 if received scholarship, 0 otherwise
covariatesOther observable characteristics.VariousAge, Gender, Socioeconomic Status

Logical Relationship Diagram

RD_Logic Forcing_Variable Forcing Variable (e.g., Test Score) Cutoff Cutoff Forcing_Variable->Cutoff Compared to Outcome Outcome (e.g., Future Earnings) Forcing_Variable->Outcome Direct Effect Treatment Treatment (e.g., Scholarship) Cutoff->Treatment Determines Treatment->Outcome Causal Effect Confounders Unobserved Confounders Confounders->Forcing_Variable Confounders->Outcome

Regression Discontinuity Design Logic

Difference-in-Differences (DID) Design

The Difference-in-Differences (DID) method is a quasi-experimental technique that estimates the causal effect of a specific intervention by comparing the change in outcomes over time between a treatment group and a control group.[11][13] It is a powerful tool for analyzing the impact of policies or events.

Conceptual Overview

DID requires data from at least two time periods (before and after the intervention) for both a group that receives the treatment and a group that does not. The "first difference" is the change in the outcome for each group before and after the treatment. The "second difference" is the difference in these changes between the two groups. This double-differencing removes biases from time trends and permanent differences between the groups.[11]

Key Assumptions

The validity of the DID estimator hinges on the following assumptions:

AssumptionDescription
Parallel Trends In the absence of the treatment, the average change in the outcome for the treatment group would have been the same as the average change in the outcome for the control group.[11] This is the most critical assumption.
No Spillover Effects The treatment should only affect the treatment group and not the control group.
Stable Group Composition The composition of the treatment and control groups should not change over time in a way that is related to the treatment.
Experimental Protocol

  • Data Preparation: The data should be in a "long" format, with one row per individual per time period.[14] Create a binary variable for the treatment group (1 if in the treatment group, 0 otherwise) and a binary variable for the time period (1 for the post-treatment period, 0 for the pre-treatment period).[6]

  • Graphical Analysis: Plot the average outcomes for both the treatment and control groups over time. This allows for a visual inspection of the parallel trends assumption in the pre-treatment periods.[1]

  • Estimation: The DID estimate can be obtained by running a linear regression model with the outcome variable as the dependent variable and the treatment group indicator, the time period indicator, and an interaction term between the two as independent variables.[6][13] The coefficient on the interaction term represents the DID estimate of the treatment effect.[13]

  • Validity Checks:

    • Placebo Tests: If there are multiple pre-treatment periods, conduct DID analyses using only these periods. A non-zero effect would suggest that the parallel trends assumption is violated.[1]

    • Alternative Control Groups: If possible, repeat the analysis with a different control group to see if the results are robust.[1]

    • Alternative Outcome: Use an outcome variable that is not expected to be affected by the treatment. The DID estimate for this outcome should be zero.[1]

Data Presentation: Required Data Structure
Variable NameDescriptionData TypeExample
individual_idA unique identifier for each individual.Identifier1, 2, 3...
time_periodAn indicator for the time period.Categorical/Numeric2020, 2021
treatment_groupA binary indicator for the treatment group.Binary (0/1)1 if treated, 0 if control
outcomeThe outcome variable of interest.Continuous/DiscreteIncome
covariatesOther observable characteristics.VariousAge, Education

Logical Relationship Diagram

DID_Logic cluster_pre Pre-Treatment Period cluster_post Post-Treatment Period T0 Treatment Group (T0) T1 Treatment Group (T1) T0->T1 Change over time C0 Control Group (C0) C1 Control Group (C1) C0->C1 Change over time (Parallel Trend) Treatment_Effect Treatment Effect T1->Treatment_Effect Difference C1->Treatment_Effect Difference IV_Logic Instrument Instrumental Variable (Z) Endogenous_Variable Endogenous Variable (X) Instrument->Endogenous_Variable Relevance Outcome Outcome (Y) Endogenous_Variable->Outcome Causal Effect of Interest Unobserved_Confounder Unobserved Confounder (U) Unobserved_Confounder->Endogenous_Variable Unobserved_Confounder->Outcome

References

Application Notes & Protocols: Implementing Stepwise Regression for Model Selection in Complex Datasets

Author: BenchChem Technical Support Team. Date: December 2025

Audience: Researchers, scientists, and drug development professionals.

Introduction

In the era of precision medicine and high-throughput screening, researchers in drug development are often faced with complex, high-dimensional datasets.[1][2] Identifying the most relevant variables from a vast pool of candidates is crucial for building accurate predictive models, understanding disease mechanisms, and discovering novel drug targets.[3][4] Stepwise regression is an automated statistical technique designed to build a regression model by iteratively adding or removing predictor variables based on their statistical significance.[5][6][7] This method is particularly useful in the exploratory stages of analysis when theoretical knowledge is insufficient to pre-specify a model.[8][9][10] It aims to find a parsimonious model that balances predictive power with simplicity, avoiding issues like overfitting and multicollinearity that can arise from including too many predictors.[11]

This document provides a detailed guide to the methodology, application, and protocols for implementing stepwise regression, with a focus on its relevance in complex datasets encountered in drug development.

Methodology of Stepwise Regression

Stepwise regression automates the variable selection process by systematically adding or removing variables from a model.[12] The selection is based on a predefined criterion, typically a measure of statistical significance or model fit, such as p-values, Akaike Information Criterion (AIC), or Bayesian Information Criterion (BIC).[5][13][14][15] There are three primary approaches to stepwise regression.[10][16][17]

  • Forward Selection: This method starts with a null model (containing no predictors) and iteratively adds the most statistically significant variable at each step.[17][18] The process continues until no remaining variable meets the predefined entry criterion (e.g., a p-value below a certain threshold).[12][19]

  • Backward Elimination: This approach begins with a full model that includes all candidate predictors.[18][20] It then iteratively removes the least statistically significant variable at each step.[17] This continues until all variables remaining in the model meet a specified significance level.[20][21] Backward elimination requires that the number of data samples (n) is larger than the number of variables (p) to fit the initial full model.[17]

  • Bidirectional (Stepwise) Elimination: This is a hybrid of the forward and backward methods.[10][16] It starts like forward selection by adding significant variables. However, after each addition, it assesses all variables already in the model to see if any have become redundant and can be removed.[22][23] This allows the procedure to reconsider variables that were added in previous steps.[20]

The logical flow of these three methods is illustrated below.

Stepwise_Methodology cluster_forward Forward Selection cluster_backward Backward Elimination cluster_bidirectional Bidirectional Elimination start_f Start (Null Model) check_f Any variable meets entry criterion? start_f->check_f add_var_f Add Most Significant Variable add_var_f->check_f check_f->add_var_f Yes end_f Final Model check_f->end_f No start_b Start (Full Model) check_b Any variable meets exit criterion? start_b->check_b remove_var_b Remove Least Significant Variable remove_var_b->check_b check_b->remove_var_b Yes end_b Final Model check_b->end_b No start_s Start (Null Model) check_add Add? start_s->check_add add_var_s Add Variable (Forward Step) check_remove Remove? add_var_s->check_remove remove_var_s Remove Variable (Backward Step) remove_var_s->check_add check_add->add_var_s Yes end_s Final Model check_add->end_s No check_remove->remove_var_s Yes check_remove->check_add No

Figure 1: Logical flow of stepwise regression methodologies.

Application in Drug Development & Research

Stepwise regression can be a valuable tool for exploratory data analysis in various stages of drug discovery and development.

  • Quantitative Structure-Activity Relationship (QSAR): In QSAR studies, regression models are built to predict the biological activity of chemical compounds based on their structural or physicochemical properties (descriptors).[24] Given the large number of possible descriptors, stepwise regression can help identify a smaller subset that is most predictive of activity, aiding in lead optimization.[3][24]

  • Biomarker Discovery: When analyzing high-dimensional data from genomics, proteomics, or metabolomics, stepwise regression can be used to screen for potential biomarkers associated with disease state, progression, or response to treatment.[2] For example, it can help identify a panel of genes whose expression levels are predictive of a patient's prognosis.

  • Clinical Trial Data Analysis: In clinical trials, stepwise regression can help identify demographic, clinical, or genetic factors that are significant predictors of patient outcomes or response to an investigational drug.[25]

The workflow below illustrates how stepwise regression fits into a typical bioinformatics pipeline for biomarker discovery.

Drug_Discovery_Workflow data_acq Data Acquisition (e.g., RNA-Seq, Proteomics) preprocessing Data Preprocessing (Normalization, Cleaning) data_acq->preprocessing feature_eng Feature Engineering & Initial Filtering preprocessing->feature_eng stepwise Stepwise Regression (Variable Selection) feature_eng->stepwise model_build Build Final Predictive Model (Using selected variables) stepwise->model_build validation Model Validation (Cross-Validation, External Data) model_build->validation validation->stepwise Iterate/Refine biomarker Candidate Biomarker Signature validation->biomarker

Figure 2: Workflow for biomarker discovery using stepwise regression.

Protocol for Stepwise Regression Analysis

This protocol outlines the steps for performing stepwise regression using the R programming language, which is widely used in bioinformatics and statistical analysis. The step() function from the built-in stats package is a common tool for this purpose.[26]

3.1 Experimental Design (Data & Model Specification)

  • Define Objective: Clearly state the research question. Identify the dependent (outcome) variable and the pool of candidate independent (predictor) variables.

  • Data Preparation:

    • Load the dataset into R.

    • Clean the data: Handle missing values (e.g., through imputation or removal), and address outliers.

    • Ensure data types are correct (e.g., numeric, factor).

    • Partition the data into training and testing sets to allow for model validation.[6]

  • Model Scope: Define the simplest model (lower scope) and the most complex model (upper scope) for the selection process. Typically, the lower scope is an intercept-only model, and the upper scope is the full model with all candidate predictors.

3.2 Stepwise Regression Protocol in R

The following R code provides a template for performing bidirectional stepwise regression.

3.3 Interpreting the Output

The summary(stepwise_model) command will produce a detailed output. Key components to interpret include:

  • Coefficients: The estimated coefficients for the selected variables, their standard errors, t-values, and p-values.[27][28]

  • R-squared and Adjusted R-squared: These values indicate the proportion of variance in the dependent variable that is explained by the model.[27][28] The adjusted R-squared is generally preferred as it accounts for the number of predictors in the model.[28]

  • F-statistic and p-value: These indicate the overall significance of the model.[28]

Data Presentation and Results

The output of a stepwise regression procedure is often presented in a table that summarizes the model-building process at each step. This allows for a clear comparison of how model fit statistics change as variables are added or removed.

Table 1: Example Summary of a Forward Selection Process

StepVariable AddedVariables in ModelR-squaredAdjusted R-squaredAIC
1Gene_A_exprGene_A_expr0.4520.448251.7
2Drug_DoseGene_A_expr, Drug_Dose0.6130.605210.4
3AgeGene_A_expr, Drug_Dose, Age0.6890.678195.3
4-No further improvement---

This table illustrates a hypothetical forward selection where variables are added sequentially, improving model fit (increasing Adj. R-squared and decreasing AIC) until no further significant improvement is possible.

Table 2: Final Model Coefficients from Stepwise Regression

VariableCoefficient (B)Std. Errort-valuep-value
(Intercept)52.582.2922.9_< 0.001
Gene_A_expr1.470.159.8_< 0.001
Drug_Dose0.660.0513.2_< 0.001
Age-0.240.09-2.7_0.015

This table presents the final selected variables and their coefficients, which indicate the magnitude and direction of their effect on the outcome variable.[27][28]

Important Considerations and Alternatives

While computationally efficient, stepwise regression has several well-documented limitations that researchers must consider.[10][29]

5.1 Disadvantages and Caveats

  • Overfitting: The method can capitalize on chance correlations in the data, leading to models that perform well on the training data but poorly on new data.[11][16]

  • Bias: The p-values and coefficient estimates of the final model are biased because the variable selection process involves multiple testing, which is not accounted for in the final model's summary statistics.[18][30]

  • Instability: The selected model can be highly sensitive to small changes in the data.[11][31]

  • Suboptimal Model: It is a greedy algorithm that makes locally optimal choices at each step and is not guaranteed to find the absolute best model from all possible subsets.[22][29]

5.2 Alternatives to Stepwise Regression

Given its drawbacks, it is often recommended to compare the results of stepwise regression with other variable selection techniques.

  • Best Subset Regression: This method evaluates all possible models for a given number of predictors and identifies the best one based on a chosen criterion (e.g., Adjusted R-squared, Mallows' Cp).[8] It is more computationally intensive but more exhaustive than stepwise.

  • Penalized (Regularization) Methods: Techniques like LASSO (Least Absolute Shrinkage and Selection Operator) and Ridge Regression are highly favored, especially for high-dimensional data.[11][29] LASSO performs variable selection by shrinking the coefficients of less important variables to exactly zero, effectively removing them from the model.[29] These methods are generally considered more robust against overfitting than stepwise regression.[1][25][32]

Alternatives_Comparison main Variable Selection Methods stepwise Stepwise Regression (Greedy Search) main->stepwise best_subset Best Subset Regression (Exhaustive Search) main->best_subset lasso LASSO / Ridge (Penalization/Shrinkage) main->lasso step_pro Pros: - Fast - Simple to implement stepwise->step_pro step_con Cons: - Suboptimal - Biased p-values - Unstable stepwise->step_con best_pro Pros: - Finds optimal model for each subset size best_subset->best_pro best_con Cons: - Computationally intensive - Can overfit best_subset->best_con lasso_pro Pros: - Handles high dimensions (p > n) - Reduces overfitting - Continuous shrinkage lasso->lasso_pro lasso_con Cons: - Can be complex to tune - Tends to select one from a group of correlated variables lasso->lasso_con

Figure 3: Comparison of stepwise regression with alternative methods.

Conclusion

Stepwise regression is a straightforward and computationally efficient method for automated variable selection in complex datasets.[10][29] It can be a valuable exploratory tool for researchers in drug development to generate hypotheses and identify a manageable subset of potentially important predictors from a large pool of variables.[9] However, its use should be approached with caution due to its significant limitations, including the risk of overfitting and model instability.[11][16][18] It is highly recommended that stepwise regression be used as a preliminary step in the model-building process and that its results be validated rigorously and compared with more robust modern techniques like LASSO regression.[8][33]

References

Troubleshooting & Optimization

How to detect and deal with multicollinearity in a regression model.

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides troubleshooting and answers to frequently asked questions regarding the detection and management of multicollinearity in regression models.

Frequently Asked Questions (FAQs)

Q1: What is multicollinearity?

A1: Multicollinearity is a statistical issue that arises in a regression model when two or more independent variables are highly correlated with each other.[1][2][3][4] This strong linear relationship means that the variables do not provide unique or independent information to the model.[5]

Q2: Why is multicollinearity a problem for my regression model?

A2: While multicollinearity does not necessarily reduce the overall predictive power of the model, it can create several problems for the interpretation of the results:[6]

  • Unreliable Coefficient Estimates: The estimated coefficients of the correlated variables can become unstable and have high standard errors.[6][7] This makes them very sensitive to small changes in the data or model specification.[8]

  • Difficulty in Assessing Variable Importance: Due to the inflated standard errors, it becomes challenging to determine the individual effect of each predictor on the dependent variable.[6][9] You may see statistically insignificant coefficients for variables that are theoretically important.

  • Misleading Interpretations: The signs of the regression coefficients may be counterintuitive or opposite to what is expected based on domain knowledge.[8]

Q3: What are the common causes of multicollinearity?

A3: Multicollinearity can arise from several sources:

  • Data Collection Issues: The way data is collected can inadvertently lead to correlated variables.

  • Model Specification: Including variables that are transformations of other variables in the model (e.g., including both x and x^2) can introduce multicollinearity.[2]

  • Over-defined Model: Having more predictor variables than observations can lead to multicollinearity.[10]

  • Inherent Relationships: Some variables are naturally correlated. For example, in drug development, dosage and exposure levels are often highly correlated.

Troubleshooting Guide: Detecting and Dealing with Multicollinearity

This section provides a step-by-step guide to identify and address multicollinearity in your regression models.

Step 1: Detecting Multicollinearity

There are several methods to detect the presence of multicollinearity. It is often best to use a combination of these techniques.

Method 1: Correlation Matrix

A straightforward initial step is to examine the correlation matrix of the predictor variables.

  • Experimental Protocol:

    • Calculate the pairwise correlation coefficients for all independent variables in your model.

    • Look for high absolute correlation coefficients (typically > 0.7 or 0.8) between pairs of variables.[5][8] A high value suggests a strong linear relationship.

  • Limitations: This method can only detect pairwise correlations and may miss more complex relationships where three or more variables are intercorrelated.[8][11]

Method 2: Variance Inflation Factor (VIF)

The Variance Inflation Factor is a more robust metric that quantifies how much the variance of an estimated regression coefficient is inflated due to its correlation with other predictors.[2][7][9][11]

  • Experimental Protocol:

    • For each independent variable, perform a regression where it is the dependent variable and all other independent variables are the predictors.

    • Calculate the R-squared value from this regression.

    • The VIF for that variable is calculated as: VIF = 1 / (1 - R^2)

    • Repeat this for all independent variables.

  • Data Interpretation: The VIF values can be interpreted using the following guidelines:

VIF ValueInterpretationRecommended Action
1No correlationNone
1 - 5Moderate correlationMay warrant further investigation[2][11]
> 5High correlationIndicates a potential issue with multicollinearity[1][12][13]
> 10Very high correlationSerious multicollinearity, requires correction[11][12]

Method 3: Principal Component Analysis (PCA)

PCA is a dimensionality reduction technique that can also be used to diagnose multicollinearity by examining the eigenvalues of the correlation matrix of the predictors.[5][14]

  • Experimental Protocol:

    • Perform a Principal Component Analysis on the independent variables.

    • Examine the eigenvalues of the principal components.

  • Data Interpretation:

    • Near-zero eigenvalues: If one or more eigenvalues are close to zero, it indicates that there are linear dependencies among the variables.[14]

    • High Variance Concentration: If a small number of principal components explain a very large proportion of the variance in the predictors, it suggests that the original variables are highly correlated.[14]

Step 2: Dealing with Multicollinearity

Once multicollinearity is detected, several approaches can be taken to mitigate its effects.

Approach 1: Remove Highly Correlated Variables

The simplest solution is to remove one or more of the highly correlated variables from the model.[1][5][12][15]

  • Methodology:

    • Identify the variables with high VIFs.

    • Based on domain knowledge, decide which variable is less important or more redundant and remove it from the model.

    • Re-run the regression and check the VIFs again.

Approach 2: Combine Correlated Variables

Instead of removing variables and losing information, you can combine the correlated variables into a single new variable.[15]

  • Methodology:

    • Feature Engineering: Create a new composite variable that represents the combined effect of the correlated variables. For example, if you have highly correlated measures of drug exposure, you could create an average exposure variable.

    • Principal Component Analysis (PCA): Use PCA to transform the original correlated variables into a smaller set of uncorrelated principal components.[12][15][16][17] You can then use these principal components as predictors in your regression model.[17]

Approach 3: Use Regularized Regression Models

Regularized regression methods are designed to handle multicollinearity by adding a penalty term to the loss function, which shrinks the coefficient estimates.

  • Ridge Regression: This method is particularly effective at handling multicollinearity.[3][6][10][18][19] It adds a penalty proportional to the square of the magnitude of the coefficients (L2 penalty).[18] This shrinks the coefficients of correlated variables towards each other.

  • Lasso Regression: This method adds a penalty proportional to the absolute value of the magnitude of the coefficients (L1 penalty). It can shrink the coefficients of less important variables to exactly zero, effectively performing variable selection.

  • Elastic Net Regression: This is a combination of Ridge and Lasso regression, incorporating both L1 and L2 penalties.

Visual Workflows

The following diagrams illustrate the process of detecting and dealing with multicollinearity.

G cluster_detection Detection Phase Start Start with Regression Model CorrMatrix Calculate Correlation Matrix Start->CorrMatrix VIF Calculate Variance Inflation Factors (VIFs) Start->VIF PCA_Detect Perform PCA on Predictors Start->PCA_Detect CheckCorr High Pairwise Correlations? CorrMatrix->CheckCorr CheckVIF VIF > 5? VIF->CheckVIF CheckPCA Near-Zero Eigenvalues? PCA_Detect->CheckPCA MultiDetected Multicollinearity Detected CheckCorr->MultiDetected Yes NoMulti No Significant Multicollinearity CheckCorr->NoMulti No CheckVIF->MultiDetected Yes CheckVIF->NoMulti No CheckPCA->MultiDetected Yes CheckPCA->NoMulti No

Caption: Workflow for detecting multicollinearity.

G cluster_remediation Remediation Phase Input Multicollinearity Detected Remove Remove Correlated Variables Input->Remove Combine Combine Correlated Variables Input->Combine Regularize Use Regularized Regression Input->Regularize FinalModel Final Model Remove->FinalModel PCA_Combine e.g., PCA Combine->PCA_Combine Ridge e.g., Ridge Regression Regularize->Ridge PCA_Combine->FinalModel Ridge->FinalModel

Caption: Strategies for dealing with multicollinearity.

References

What to do when the linearity assumption in regression is violated.

Author: BenchChem Technical Support Team. Date: December 2025

Technical Support Center: Regression Analysis

This guide provides troubleshooting and answers to frequently asked questions regarding the violation of the linearity assumption in regression analysis, a common challenge encountered by researchers, scientists, and drug development professionals.

Frequently Asked Questions (FAQs)

Q1: What is the linearity assumption in regression analysis?

The linearity assumption posits that the relationship between the independent variable(s) and the dependent variable is linear.[1][2][3] This means that a change in the independent variable is associated with a proportional change in the dependent variable.[4] When fitting a linear regression model, we are essentially trying to fit a straight line to our data that best represents this relationship.[1][5]

Q2: What are the consequences of violating the linearity assumption?

Violating the linearity assumption can have serious consequences for your model.[2] If the true relationship is non-linear, a linear model will fail to capture the underlying pattern in the data.[1][6] This can lead to:

  • Biased coefficient estimates: The model will not accurately represent the true impact of the independent variables.[6]

  • Inaccurate predictions: The model will systematically over- or under-predict the outcome variable at different points.[6][7]

Q3: How can I detect a violation of the linearity assumption?

The most common method for detecting non-linearity is through visual inspection of residual plots.[6][8] Specifically, a plot of the residuals versus the predicted values is a powerful diagnostic tool.[2][6][8]

  • What to look for: If the linearity assumption holds, the points in the residual plot should be randomly scattered around the horizontal line at zero.[2][8]

  • Signs of violation: A clear pattern, such as a U-shape or a systematic curve in the residuals, indicates that the linearity assumption has been violated.[6][8]

Another approach is to create a scatter plot of the dependent variable against each independent variable to visually check for a linear relationship.[3][9]

Troubleshooting Guides

Issue: My residual plot shows a clear pattern, suggesting a non-linear relationship. What should I do?

When you've identified a non-linear relationship, you have several options to address it. The appropriate method depends on the nature of the non-linearity and the goals of your analysis.

logical_relationship Start Linearity Assumption Violated? Transform 1. Transform Variables Start->Transform Yes Poly 2. Polynomial Regression Start->Poly Yes GAM 3. Generalized Additive Models (GAMs) Start->GAM Yes Proceed Proceed with Linear Regression Start->Proceed No ReEvaluate Re-evaluate Model Fit Transform->ReEvaluate Poly->ReEvaluate GAM->ReEvaluate

Caption: Decision process for addressing linearity violations.

Solution 1: Variable Transformations

This is often the simplest approach to handling non-linearity. By applying a mathematical function to the independent and/or dependent variables, you can sometimes linearize the relationship.[8][9][10]

Experimental Protocol: Applying a Logarithmic Transformation

A logarithmic transformation is particularly useful when the data exhibits exponential growth or is right-skewed.[9][11]

  • Assess the Data: Ensure all values of the variable to be transformed are positive, as the logarithm of a non-positive number is undefined.[8]

  • Apply the Transformation: Create a new variable by taking the natural logarithm (ln) of the original variable. In R, you would use the log() function.[11]

  • Fit the New Model: Run the regression analysis using the transformed variable(s).

  • Re-check Assumptions: Create a new residual plot to confirm that the transformation has resolved the non-linearity issue. It's important to re-check all model assumptions, as a transformation can sometimes affect others, like homoscedasticity.[12]

Table 1: Common Variable Transformations

TransformationFormulaWhen to Use
Logarithmic log(X)For relationships that appear exponential.[13][14]
Square Root sqrt(X)Useful for reducing right skewness; less extreme than a log transformation.
Reciprocal 1/XWhen the effect of the predictor decreases as its value increases.
Square X^2To model a simple quadratic relationship.[4]

Solution 2: Polynomial Regression

If a simple transformation doesn't work, you can fit a curve to the data by adding polynomial terms (e.g., X², X³) of the independent variables to the model.[15][16][17] This allows the regression line to bend to better fit the data.[5][16]

Experimental Protocol: Implementing Polynomial Regression

  • Visualize the Relationship: A scatter plot can help suggest the degree of the polynomial needed (e.g., one curve suggests a quadratic term, X²).[15]

  • Create Polynomial Features: Generate new predictor variables by squaring, cubing, etc., the original independent variable. Many statistical packages have functions to do this automatically (e.g., PolynomialFeatures in Scikit-Learn).[15][18]

  • Fit the Model: Run a multiple linear regression including the original and the new polynomial terms.

  • Evaluate the Model: Check if the added terms are statistically significant and have improved the model fit (e.g., using R-squared). Be cautious of overfitting; a very high-degree polynomial might fit the sample data perfectly but perform poorly on new data.[19]

Solution 3: Generalized Additive Models (GAMs)

GAMs are a more flexible and powerful extension of linear models.[20] Instead of fitting a single straight line, GAMs fit a sum of smooth, non-linear functions to the predictors.[19][21][22] This allows the model to learn the shape of the relationship from the data itself without you needing to specify the exact form (like quadratic or cubic) beforehand.[21][23]

Advantages of GAMs:

  • Flexibility: Can capture complex, non-linear patterns that polynomial regression might miss.[20][21]

  • Automation: The smoothness of the functions is determined automatically during model fitting, reducing the risk of overfitting.[21]

  • Interpretability: While more complex than linear models, GAMs are more interpretable than "black box" machine learning algorithms, as the contribution of each predictor can still be visualized and analyzed.[20][21]

Troubleshooting Workflow

This workflow outlines the systematic steps to diagnose and treat linearity assumption violations.

experimental_workflow cluster_solutions 3. Apply Corrective Method Start 1. Fit Initial Linear Regression Model Diagnose 2. Diagnose Linearity (Plot Residuals vs. Predicted) Start->Diagnose Check Is there a pattern? Diagnose->Check Transform A. Try Variable Transformation Check->Transform Yes Poly B. Fit Polynomial Regression Check->Poly Yes GAM C. Use Generalized Additive Model (GAM) Check->GAM Yes Finalize 5. Finalize and Report Model Check->Finalize No Evaluate 4. Evaluate New Model Fit (Check R-squared, Residuals, etc.) Transform->Evaluate Poly->Evaluate GAM->Evaluate Evaluate->Finalize

Caption: Workflow for addressing non-linearity in regression.

Summary of Methods

Table 2: Comparison of Methods for Handling Non-Linearity

MethodDescriptionAdvantagesDisadvantages
Variable Transformation Applies a function (e.g., log, sqrt) to variables to linearize the relationship.[10][24]Simple to implement; can also help with other assumption violations like heteroscedasticity.[1][24]May not work for complex relationships; interpretation of coefficients can be less straightforward.[13][25]
Polynomial Regression Adds higher-order terms of predictors (X², X³) to the model to fit a curve.[15][18]Can model simple non-linear trends; stays within the linear regression framework.[11][12]Prone to overfitting with high-degree polynomials; can be unstable at the boundaries of the data.[17][19]
Generalized Additive Models (GAMs) Models the outcome as a sum of flexible, smooth functions of the predictors.[19][22]Highly flexible for complex relationships; less prone to overfitting than high-degree polynomials.[21][23]Can be computationally more intensive; interpretation is more complex than a simple linear model.

References

Diagnosing and addressing heteroscedasticity in your data.

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides researchers, scientists, and drug development professionals with resources to diagnose and address heteroscedasticity in their experimental data.

Frequently Asked Questions (FAQs)

Q1: What is heteroscedasticity?

A1: Heteroscedasticity refers to the situation where the variance of the errors (or residuals) in a regression model is not constant across all levels of the independent variables.[1][2] In simpler terms, the spread of the data points around the regression line is unequal.[3] This violates a key assumption of ordinary least squares (OLS) regression, which assumes homoscedasticity (constant variance).[3][4]

Q2: Why is heteroscedasticity a problem in my experimental data?

A2: While heteroscedasticity does not introduce bias into the coefficient estimates of a regression model, it does have serious consequences for the reliability of your results.[4][5] Specifically, it leads to:

  • Biased Standard Errors: The standard errors of the regression coefficients become unreliable.[6][7] Typically, they are underestimated.[1]

  • Inefficient Estimators: The OLS estimators are no longer the Best Linear Unbiased Estimators (BLUE), meaning they do not have the minimum variance among all unbiased estimators.[8]

Q3: What are the common causes of heteroscedasticity in scientific research?

A3: Heteroscedasticity can arise from several sources in experimental data:

  • Omitted Variables: If a relevant variable is excluded from the model, its effect is captured by the error term, which can lead to non-constant variance.[2][9]

  • Incorrect Functional Form: Assuming a linear relationship when the true relationship is non-linear can manifest as heteroscedasticity.[3][10]

  • Measurement Error: If the precision of a measurement changes across different levels of a variable, it can introduce heteroscedasticity.

  • Outliers: Extreme values in the dataset can disproportionately influence the variance of the residuals.[8]

  • Data Transformation Issues: Applying an incorrect data transformation can induce heteroscedasticity.[8]

Troubleshooting Guides

Guide 1: Diagnosing Heteroscedasticity

This guide outlines the steps to determine if heteroscedasticity is present in your data.

A common initial step is to visually inspect the residuals of your regression model.

  • Methodology:

    • Fit your regression model using Ordinary Least Squares (OLS).

    • Plot the residuals of the model against the fitted (predicted) values.

    • Examine the scatterplot for any systematic patterns.

  • Interpretation:

    • Homoscedasticity: The points will be randomly scattered around the horizontal axis, with a roughly constant spread.

    • Heteroscedasticity: A tell-tale sign is a "fan" or "cone" shape, where the spread of the residuals increases or decreases as the fitted values change.[2][4][10][11]

For a more rigorous diagnosis, you can use formal statistical tests. The two most common are the Breusch-Pagan test and the White test.

  • Breusch-Pagan Test: This test assesses whether the variance of the residuals is dependent on the independent variables.[9][10][11]

  • White Test: This is a more general test that can also detect non-linear forms of heteroscedasticity.[11][12][13]

The null hypothesis for both tests is that homoscedasticity is present.[5] A p-value below a chosen significance level (e.g., 0.05) indicates the presence of heteroscedasticity.[5]

TestKey Features
Breusch-Pagan Test Tests for a linear relationship between the residual variance and the independent variables.
White Test More general; it tests for both linear and non-linear relationships between the residual variance and the independent variables, as well as their cross-products.[12][13][14]
Experimental Protocols: Diagnostic Tests

  • Fit the OLS Regression Model: Run your primary regression and obtain the residuals.

  • Square the Residuals: Calculate the squared residuals for each observation.

  • Auxiliary Regression: Fit a new regression model where the squared residuals are the dependent variable and the original independent variables are the predictors.[5]

  • Calculate the Test Statistic: The test statistic is calculated as n * R², where 'n' is the sample size and 'R²' is the coefficient of determination from the auxiliary regression.[5]

  • Determine Significance: Compare the test statistic to a chi-square distribution with degrees of freedom equal to the number of independent variables in the auxiliary regression. A significant p-value suggests heteroscedasticity.[5]

  • Fit the OLS Regression Model: Run your primary regression and obtain the residuals.

  • Square the Residuals: Calculate the squared residuals for each observation.

  • Auxiliary Regression: Fit a new regression model where the squared residuals are the dependent variable. The independent variables in this model include the original predictors, their squared terms, and all their cross-products.[12][13]

  • Calculate the Test Statistic: The test statistic is n * R² from this auxiliary regression.[12][13]

  • Determine Significance: Compare the test statistic to a chi-square distribution with degrees of freedom equal to the number of predictors in the auxiliary regression (excluding the intercept). A significant p-value indicates heteroscedasticity.[12]

Guide 2: Addressing Heteroscedasticity

Once diagnosed, heteroscedasticity can be addressed using several methods.

Transforming the dependent variable can often stabilize the variance.

  • Log Transformation: Taking the natural logarithm of the dependent variable is a common approach, especially when the variance of the residuals increases with the mean.[15] This transformation compresses the scale of the data, which can reduce heteroscedasticity.[16]

  • Box-Cox Transformation: This is a more general power transformation that can help find an optimal transformation to stabilize variance.[7][17][18] The transformation is defined as:

    • (y^λ - 1) / λ, if λ ≠ 0

    • ln(y), if λ = 0 The optimal value of λ is typically chosen to maximize a log-likelihood function.[18][19]

TransformationWhen to UseConsiderations
Log Transformation When the standard deviation of the residuals is proportional to the fitted values.The dependent variable must be positive.[7]
Square Root Transformation When the variance of the residuals is proportional to the fitted values.The dependent variable must be non-negative.
Box-Cox Transformation When the relationship between variance and the mean is not clear, this method can help identify a suitable power transformation.The dependent variable must be positive.[7]

This approach corrects the standard errors for heteroscedasticity without changing the coefficient estimates.[9] These are often referred to as White's robust standard errors.[15] This is a good option when you are confident in the specification of your model but need to correct for the unreliable standard errors.[3]

WLS is a modification of OLS that assigns a weight to each observation, with lower weights given to observations with higher variance.[2][6] This method is particularly useful when the form of heteroscedasticity is known or can be estimated.

  • Determining the Weights: The weights are typically the inverse of the variance of the residuals.[6] If the exact variances are unknown, they can be estimated. For example, if the variance is proportional to an independent variable x, the weights would be 1/x.[6]

Visualizing the Workflow

The following diagrams illustrate the process of diagnosing and addressing heteroscedasticity.

G start Start: Have a Fitted Regression Model visual_inspection Step 1: Visual Inspection (Residuals vs. Fitted Plot) start->visual_inspection pattern Is there a pattern (e.g., fan or cone shape)? visual_inspection->pattern formal_test Step 2: Formal Statistical Test (Breusch-Pagan or White Test) pattern->formal_test Yes homoscedastic Conclusion: Homoscedasticity (No further action needed) pattern->homoscedastic No significant Is the test statistic significant (p < 0.05)? formal_test->significant significant->homoscedastic No heteroscedastic Conclusion: Heteroscedasticity Detected significant->heteroscedastic Yes

Caption: Workflow for Diagnosing Heteroscedasticity.

G start Heteroscedasticity Detected consider_cause Consider the potential cause (e.g., omitted variable, wrong functional form) start->consider_cause remedy Choose a remedy start->remedy Cause unknown or unaddressable address_cause Address the root cause if possible (e.g., add variables, change model) consider_cause->address_cause retest Re-run diagnostic tests address_cause->retest retest->remedy Still present end Model Corrected retest->end Resolved transformation Data Transformation (Log, Box-Cox) remedy->transformation robust_se Use Robust Standard Errors (Huber-White) remedy->robust_se wls Weighted Least Squares (WLS) remedy->wls transformation->end robust_se->end wls->end

Caption: Logical Flow for Addressing Heteroscedasticity.

References

Technical Support Center: Addressing Non-Constant Variance in Regression Models

Author: BenchChem Technical Support Team. Date: December 2025

This technical support center provides troubleshooting guides and frequently asked questions (FAQs) for researchers, scientists, and drug development professionals who encounter non-constant variance of error terms (heteroscedasticity) in their regression analyses.

Frequently Asked Questions (FAQs)

Q1: What is non-constant variance of error terms (heteroscedasticity)?

In regression analysis, one of the key assumptions of Ordinary Least Squares (OLS) is that the error terms (residuals) have a constant variance across all levels of the independent variables. This is known as homoscedasticity. Non-constant variance, or heteroscedasticity, occurs when this assumption is violated, meaning the spread of the residuals is not consistent across the range of predicted values.[1][2][3] This can often be visualized as a cone or fan shape in a plot of residuals versus fitted values.[1][2]

Q2: Why is non-constant variance a problem in regression analysis?

Heteroscedasticity poses a significant issue because while the OLS coefficient estimates remain unbiased, they are no longer the Best Linear Unbiased Estimators (BLUE).[2][4] The primary consequences are:

  • Inefficient Coefficient Estimates: The OLS estimators are no longer the most efficient, meaning their variance is not minimized.[5]

Q3: What are the common causes of non-constant variance?

Several factors can lead to heteroscedasticity in your experimental data:

  • Outliers: Extreme values in the dataset can disproportionately influence the variance of the residuals.[2][5]

  • Model Misspecification: Omitting a relevant variable from the model can cause its effect to be captured by the error term, leading to non-constant variance.[1][5] Similarly, using an incorrect functional form (e.g., a linear model for a non-linear relationship) can also be a cause.[5]

  • Large Range in Variable Scale: Datasets with a wide range between the smallest and largest observed values are more prone to heteroscedasticity.[1][2]

  • Error Learning: In some processes, the error magnitude might decrease over time as the system becomes more precise.[5]

Troubleshooting Guides

Issue: I have detected non-constant variance in my regression model. How do I fix it?

There are several approaches to address heteroscedasticity. The appropriate method depends on the nature of your data and the underlying cause of the non-constant variance.

Solution 1: Data Transformation

One of the simpler methods to stabilize the variance is to transform the dependent variable (Y).[1][7] This approach is often effective when the variance is proportional to the mean.

Common Transformations:

  • Log Transformation (log(Y)): Useful when the variance is proportional to the square of the mean.[8]

  • Square Root Transformation (√Y): Appropriate for count data where the variance is proportional to the mean (e.g., Poisson distribution).[8]

  • Reciprocal Transformation (1/Y): A stronger transformation, useful when the variance increases rapidly with the mean.[8]

Experimental Protocol: Applying a Variance-Stabilizing Transformation

  • Assess the Relationship: Plot the residuals against the fitted values from your original OLS regression. Observe the pattern of the variance.

  • Select a Transformation:

    • If the variance increases with the fitted values, try a log or square root transformation on your response variable.

    • If the variance decreases as the mean increases, a reciprocal transformation might be suitable.[8]

  • Re-run the Regression: Fit the regression model using the transformed dependent variable.

  • Evaluate the Residuals: Plot the residuals of the new model against the fitted values. The variance should now be more consistent.

  • Interpret with Caution: Remember that the interpretation of the coefficients will now be in terms of the transformed scale. For instance, in a log-transformed model, the coefficient represents the expected change in log(Y) for a one-unit change in the predictor.

Solution 2: Weighted Least Squares (WLS) Regression

WLS is a method that assigns a weight to each data point based on the inverse of its variance.[1][9] Observations with smaller variance are given more weight, and those with larger variance receive less weight.[4][9]

Experimental Protocol: Implementing Weighted Least Squares

  • Determine the Weights: The primary challenge in WLS is to find the appropriate weights.

    • Known Weights: In some cases, the weights may be known from theory or prior experiments. For example, if the response is an average of n observations, the weight would be n.[9]

    • Estimated Weights: More commonly, the variance of the error term is unknown and must be estimated. A common approach is to: a. Run an OLS regression and obtain the residuals, eᵢ. b. Regress the absolute or squared residuals on the predictor(s) that are thought to be related to the heteroscedasticity to get an estimate of the variance, σ̂ᵢ². c. The weights are then calculated as wᵢ = 1/σ̂ᵢ².[10]

  • Perform WLS Regression: Run the regression analysis using the calculated weights. Most statistical software packages have a specific function for WLS regression.

  • Assess the Model: Evaluate the standardized residuals of the WLS model. These should exhibit constant variance.[1][7]

Solution 3: Using Heteroscedasticity-Consistent (Robust) Standard Errors

This approach doesn't change the OLS coefficient estimates but corrects the standard errors to account for the presence of heteroscedasticity.[6][11] This is a popular method in econometrics.

Experimental Protocol: Calculating Robust Standard Errors

  • Fit the OLS Model: Run a standard OLS regression on your data.

  • Calculate Robust Standard Errors: Use statistical software to compute heteroscedasticity-consistent standard errors. Common methods include the Eicker-Huber-White estimator (often denoted as HC0, HC1, HC2, HC3, etc.).[6][12][13]

  • Re-evaluate Hypothesis Tests: Use the robust standard errors to recalculate t-statistics and p-values for your coefficient estimates. This will provide a more accurate assessment of their significance.

Data Presentation: Comparison of Corrective Methods

The following table illustrates the hypothetical results of applying different methods to a dataset exhibiting heteroscedasticity.

MethodCoefficient (β₁)Standard Errort-statisticp-value
Ordinary Least Squares (OLS) 2.500.505.00< 0.001
OLS with Robust Standard Errors 2.500.852.940.004
Weighted Least Squares (WLS) 2.450.783.140.002
Log-Transformed OLS 0.800.302.670.009

Note: The coefficient for the log-transformed model is on a different scale and not directly comparable.

Visualization of the Troubleshooting Workflow

The following diagram outlines the logical steps to diagnose and address non-constant variance in a regression model.

G start Start: Fit OLS Regression Model check_residuals Visually Inspect Residuals vs. Fitted Plot start->check_residuals formal_test Perform Formal Test (e.g., Breusch-Pagan) check_residuals->formal_test Pattern Observed homoscedastic Homoscedasticity Assumption Met check_residuals->homoscedastic No Pattern formal_test->homoscedastic p >= 0.05 heteroscedastic Heteroscedasticity Detected formal_test->heteroscedastic p < 0.05 end End: Report Results homoscedastic->end remedy Choose a Remedial Action heteroscedastic->remedy transform Transform Dependent Variable remedy->transform wls Use Weighted Least Squares (WLS) remedy->wls robust_se Use Robust Standard Errors remedy->robust_se respecify Respecify the Model remedy->respecify evaluate Re-evaluate Residuals of the New Model transform->evaluate wls->evaluate robust_se->end respecify->evaluate evaluate->homoscedastic Problem Solved evaluate->remedy Problem Persists

Caption: Workflow for diagnosing and fixing non-constant variance.

References

Common problems in regression analysis and how to fix them.

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides troubleshooting assistance for common issues encountered during regression analysis. It is intended for researchers, scientists, and drug development professionals to help diagnose and resolve potential problems in their statistical models.

Troubleshooting Workflow

Before diving into specific problems, it's helpful to have a general workflow for diagnosing your regression model. The following diagram outlines a logical sequence of checks.

G start Start: Fit Initial Regression Model check_linearity 1. Check for Non-Linearity (Residuals vs. Fitted Plot) start->check_linearity fix_linearity Fix: Apply Variable Transformation (e.g., log, polynomial) check_linearity->fix_linearity Pattern Found check_hetero 2. Check for Heteroscedasticity (Residuals vs. Fitted Plot, Breusch-Pagan Test) check_linearity->check_hetero No Pattern fix_linearity->check_hetero fix_hetero Fix: Use Robust Standard Errors or Weighted Least Squares (WLS) check_hetero->fix_hetero Pattern Found check_autocorr 3. Check for Autocorrelation (Durbin-Watson Test) (Time Series Data) check_hetero->check_autocorr No Pattern fix_hetero->check_autocorr fix_autocorr Fix: Add Lagged Variables or Use Time Series Models (ARIMA) check_autocorr->fix_autocorr Present check_multi 4. Check for Multicollinearity (VIF > 5-10) check_autocorr->check_multi Absent fix_autocorr->check_multi fix_multi Fix: Remove or Combine Correlated Predictors check_multi->fix_multi Present check_outliers 5. Check for Outliers/Leverage (Residuals vs. Leverage Plot) check_multi->check_outliers Absent fix_multi->check_outliers fix_outliers Fix: Investigate, Remove, or Use Robust Regression check_outliers->fix_outliers Present end_node End: Model is Diagnosed and Refined check_outliers->end_node Absent fix_outliers->end_node

What does a high VIF value mean in regression analysis?

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides answers to frequently asked questions and troubleshooting advice regarding the interpretation of Variance Inflation Factor (VIF) values in regression analysis.

Frequently Asked Questions (FAQs)

Q1: What is the Variance Inflation Factor (VIF)?

A: The Variance Inflation Factor (VIF) is a metric used in regression analysis to quantify the severity of multicollinearity.[1][2][3] Multicollinearity occurs when two or more independent (predictor) variables in a model are highly correlated with each other.[4][5] In essence, VIF measures how much the variance of an estimated regression coefficient is inflated because of its linear relationship with other predictors.[2][3][6] VIF is calculated for each predictor variable in the model.[7]

Q2: What does a high VIF value indicate?

A: A high VIF value for a predictor variable indicates a strong linear relationship or correlation between that variable and one or more other predictors in the model.[7][8][9] This suggests that the information provided by that predictor is not unique and is largely redundant.[3][10] A high VIF warns that the model has a multicollinearity problem, which can compromise the reliability of the results.[9]

Q3: What are the primary consequences of a high VIF in my regression model?

A: High multicollinearity, identified by high VIF values, leads to several issues that can affect the interpretation of your model:

  • Unstable Coefficient Estimates : The estimated coefficients for the correlated variables can be unstable and highly sensitive to small changes in the dataset.[2]

  • Inflated Standard Errors : Multicollinearity inflates the standard errors of the regression coefficients.[1][2][11] This makes the confidence intervals for the coefficients wider and reduces the likelihood that they will be statistically significant.[11]

  • Difficulty in Interpretation : It becomes challenging to isolate the individual effect of each correlated predictor on the dependent variable.[2][4] The model struggles to determine which variable should be credited for the effect, similar to trying to determine the individual contribution of three players tackling a quarterback simultaneously.[10]

Q4: What is considered a "high" VIF value?

A: While there is no strict, universal cutoff, several widely accepted rules of thumb are used to interpret VIF values. The appropriate threshold can depend on the specific research context and the size of the dataset.[12][13][14]

Data Presentation: VIF Value Interpretation

VIF ValueLevel of MulticollinearityInterpretation & Recommendation
1 NoneIndicates no correlation between the predictor and other variables.[2][8][9] This is the ideal scenario.
> 1 and < 5 ModerateSuggests a moderate correlation.[2][8][9] This is generally acceptable and may not require corrective action.[4][8]
≥ 5 HighIndicates a potentially problematic level of correlation.[2][4] Further investigation is warranted.[6]
≥ 10 Very High / SevereSignals serious multicollinearity.[8][10] The regression coefficients are likely poorly estimated, and corrective measures are required.[10]

Troubleshooting Guide

Q5: How do I handle high VIF values in my analysis?

A: When you detect predictors with high VIF values (e.g., >5 or >10), you should take steps to address the multicollinearity. Here are several common strategies:

  • Remove a Correlated Variable : If two or more variables are highly correlated, they supply redundant information.[10] Consider removing one of them from the model. The choice of which variable to remove can be based on theoretical grounds or by seeing which removal most improves the model's stability and VIF values.[2][10]

  • Combine Variables : If several predictors measure the same underlying construct, you can combine them into a single composite variable.[2]

  • Use Dimensionality Reduction : Techniques like Principal Component Analysis (PCA) can be used to transform the correlated predictors into a smaller set of uncorrelated components, which can then be used in the regression.[2][8][12]

  • Apply Regularization Techniques : Methods such as Ridge or Lasso regression are designed to handle multicollinearity by adding a penalty term that shrinks the coefficients of correlated predictors.[2][8][12]

Q6: Are there any situations where a high VIF can be safely ignored?

A: Yes, there are specific scenarios where a high VIF may not be a cause for concern:

  • Control Variables : If the variables with high VIFs are control variables and are not the primary variables of interest, and the variables of interest do not have high VIFs, the issue can often be ignored.[1][5] The multicollinearity among control variables does not affect the coefficients of the uncorrelated variables of interest.[5]

  • Polynomial or Interaction Terms : High VIFs are expected when you include powers (e.g., x and x²) or interaction terms (e.g., x, z, and xz) in your model, as these terms are inherently correlated with their components. This type of multicollinearity does not have adverse consequences on the model's validity.[1][5]

  • Categorical Variable Dummies : If a categorical variable with three or more categories is represented by dummy variables, you may see high VIFs if the reference category has a small proportion of cases. This is a mathematical artifact and not necessarily a problematic source of multicollinearity.[1][5]

Visualization

The following workflow diagram outlines the process for diagnosing and addressing multicollinearity using VIF.

VIF_Workflow start 1. Fit Regression Model & Calculate VIFs for all Predictors check_vif 2. Assess VIF Values start->check_vif low_vif VIFs are Acceptable (e.g., < 5) check_vif->low_vif All VIFs < 5 high_vif High VIF Detected (e.g., >= 5) check_vif->high_vif Any VIF >= 5 end_ok Proceed with Model Interpretation low_vif->end_ok investigate 3. Investigate Correlated Predictors (e.g., using a correlation matrix) high_vif->investigate solutions 4. Choose a Mitigation Strategy investigate->solutions remove Remove a Redundant Predictor solutions->remove combine Combine Predictors (e.g., create an index) solutions->combine pca_ridge Use Advanced Methods (PCA, Ridge, Lasso) solutions->pca_ridge reassess 5. Refit Model & Re-calculate VIFs remove->reassess combine->reassess pca_ridge->reassess reassess->low_vif Problem Solved reassess->high_vif Problem Persists

Caption: Workflow for diagnosing and addressing multicollinearity using VIF.

References

Technical Support Center: Troubleshooting Non-Normally Distributed Residuals in Regression Analysis

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides troubleshooting steps and answers to frequently asked questions for researchers, scientists, and drug development professionals who encounter non-normally distributed residuals in their regression models.

Frequently Asked Questions (FAQs)

Q1: What are residuals in regression analysis, and why is their distribution important?

In regression analysis, residuals are the differences between the observed values of the dependent variable and the values predicted by the model. The distribution of these residuals is a critical diagnostic tool. The assumption of normally distributed residuals is fundamental to many types of regression, particularly Ordinary Least Squares (OLS) regression. This assumption is necessary for the valid calculation of confidence intervals and p-values, which are essential for hypothesis testing and determining the statistical significance of your model's coefficients.[1][2]

Q2: How can I check if the residuals of my regression model are normally distributed?

Several graphical and statistical methods can be used to assess the normality of residuals:

  • Histograms: A histogram of the residuals should approximate a bell shape.[3]

  • Q-Q (Quantile-Quantile) Plots: This plot compares the quantiles of the residuals to the quantiles of a normal distribution. If the residuals are normally distributed, the points will fall approximately along a straight line.[4]

  • Formal Statistical Tests: Tests like the Shapiro-Wilk or Kolmogorov-Smirnov test can be used, but they can be overly sensitive to minor deviations from normality, especially with large datasets.[5]

Q3: What are the common causes of non-normally distributed residuals?

Non-normal residuals can arise from several issues in your data or model specification:

  • Outliers: Extreme values in the dataset can heavily influence the regression model and distort the distribution of residuals.[1][6]

  • Model Misspecification: The chosen model may not accurately represent the underlying relationship between the variables. This could mean a non-linear relationship is being modeled with a linear model, or important variables are omitted.[1][5][7]

  • Non-linear Relationships: If the true relationship between the independent and dependent variables is not linear, forcing a linear model will likely result in non-normally distributed residuals.[7]

  • Heteroscedasticity: This occurs when the variance of the residuals is not constant across all levels of the independent variables. It often appears as a fan or cone shape in a plot of residuals versus predicted values.[5]

  • Skewed Variables: If the dependent or independent variables are inherently skewed, it can lead to skewed residuals.[1]

Q4: What are the consequences of ignoring non-normally distributed residuals?

Troubleshooting Guides

Issue: My residuals are not normally distributed. What should I do?

Follow this step-by-step guide to diagnose and address the problem.

Decision-Making Flowchart for Handling Non-Normal Residuals

G Troubleshooting Non-Normally Distributed Residuals start Start: Non-Normal Residuals Detected check_outliers 1. Investigate Outliers start->check_outliers check_model 2. Check for Model Misspecification check_outliers->check_model note1 Are there extreme data points? check_outliers->note1 transform_data 3. Consider Data Transformation check_model->transform_data Model specification is appropriate note2 Is the relationship linear? Are all relevant variables included? check_model->note2 robust_regression 4. Use Robust Regression Methods transform_data->robust_regression Transformation is ineffective or undesirable note3 Can a function (e.g., log, sqrt) normalize the data? transform_data->note3 non_parametric 5. Employ Non-Parametric Methods robust_regression->non_parametric Robust methods are not suitable note4 Are there methods less sensitive to outliers and non-normality? robust_regression->note4 end_node End: Model Adequately Addresses Non-Normality non_parametric->end_node Non-parametric model is appropriate note5 Can a method that does not assume a specific distribution be used? non_parametric->note5

Caption: A flowchart to guide the decision-making process when faced with non-normally distributed residuals.

Summary of Methods for Handling Non-Normal Residuals

MethodDescriptionAdvantagesDisadvantagesWhen to Use
Data Transformation Applying a mathematical function (e.g., log, square root, Box-Cox) to the dependent and/or independent variables.[10][11]Can correct for non-normality and heteroscedasticity simultaneously.[3] Allows for the use of standard regression techniques.Interpretation of coefficients becomes more complex as they are on a transformed scale.[6] Not always successful in achieving normality.[10]When the residuals are skewed and a clear transformation can be justified.
Robust Regression A class of regression methods that are less sensitive to outliers and violations of the normality assumption.[12][13][14] It works by down-weighting the influence of outliers.[12][15]Provides more reliable estimates when outliers are present.[15] Does not require the removal of data points.Can be computationally more intensive. Different robust methods may yield different results.When the non-normality is primarily due to outliers or heavy-tailed distributions.
Non-Parametric Regression These methods do not assume a specific distribution for the residuals.[16] Examples include Theil-Sen regression and regression trees.[8][15][16]Flexible and not bound by the assumption of normality.[16]Often require larger sample sizes to achieve the same statistical power as parametric methods.[16] Interpretation can be less straightforward.When transformations are not effective and the relationship between variables is complex and non-linear.
Bootstrapping A resampling technique used to estimate the sampling distribution of a statistic. It can be used to obtain more accurate confidence intervals for regression coefficients when the normality assumption is violated.Does not rely on the assumption of normally distributed residuals.Can be computationally intensive.When the sample size is reasonably large and you want to obtain reliable confidence intervals without transforming the data.

Experimental Protocols

Protocol 1: Data Transformation Workflow

This protocol outlines the steps for applying a data transformation to address non-normal residuals.

Data Transformation Workflow Diagram

G Workflow for Data Transformation cluster_transforms Common Transformations start Start: Non-Normal Residuals assess_skew 1. Assess Skewness of Residuals start->assess_skew select_transform 2. Select Appropriate Transformation assess_skew->select_transform apply_transform 3. Apply Transformation to Variable(s) select_transform->apply_transform log_transform Log Transformation (for positive skew) select_transform->log_transform sqrt_transform Square Root (for moderate positive skew) select_transform->sqrt_transform boxcox_transform Box-Cox (finds optimal power transformation) select_transform->boxcox_transform rerun_regression 4. Re-run Regression Model apply_transform->rerun_regression check_residuals 5. Check Residuals of New Model rerun_regression->check_residuals interpret_results 6. Interpret Results on Transformed Scale check_residuals->interpret_results Normality Achieved fail_node End: Transformation Ineffective check_residuals->fail_node Normality Not Achieved end_node End: Residuals are Approximately Normal interpret_results->end_node

Caption: A step-by-step workflow for applying data transformations to address non-normal residuals.

Methodology:

  • Assess the nature of the non-normality:

    • Plot a histogram of the residuals to visualize their distribution.

    • Observe the direction of the skew (positive or negative).[10]

  • Select and apply a transformation:

    • For positive skew: Consider a log, square root, or reciprocal transformation of the dependent variable.[10][17]

      • Log transformation (Y' = log(Y)): Useful for data with greater skew.

      • Square root transformation (Y' = sqrt(Y)): Suitable for moderate skew.

    • For negative skew: Consider reflecting the variable (Y' = max(Y+1) - Y) and then applying a transformation for positive skew.

    • Box-Cox Transformation: This method can help identify an optimal power transformation.[11]

  • Re-evaluate the model:

    • Fit the regression model using the transformed variable(s).

    • Re-examine the residuals of the new model for normality using histograms and Q-Q plots.

  • Interpret the results:

    • Be mindful that the interpretation of the regression coefficients is now on the transformed scale.[6] For example, with a log-transformed dependent variable, the coefficient represents the change in log(Y) for a one-unit change in the independent variable.

    • If necessary, back-transform the predicted values to the original scale for reporting.[7]

Protocol 2: Implementing Robust Regression

Methodology:

  • Choose a robust regression method:

    • M-estimation: A common method that uses a function to down-weight the influence of outliers. The Huber and bisquare weighting functions are popular choices.[14]

    • Theil-Sen Estimator: A non-parametric approach that is robust to outliers.[15]

    • RANSAC (Random Sample Consensus): An iterative method that separates data into inliers and outliers and fits the model only to the inliers.[15]

  • Fit the robust regression model:

    • Use statistical software packages (e.g., R, Python, SAS) that have built-in functions for robust regression.

  • Compare with the OLS model:

    • Compare the coefficient estimates, standard errors, and overall model fit of the robust model to the original OLS model. Significant differences may indicate that outliers were heavily influencing the OLS results.

  • Report the findings:

    • Clearly state the robust method used and why it was chosen. Report the robust regression coefficients and their standard errors.

References

Why are my regression coefficients not statistically significant?

Author: BenchChem Technical Support Team. Date: December 2025

Technical Support Center: Regression Analysis

This guide provides troubleshooting steps and answers to frequently asked questions regarding non-significant regression coefficients, tailored for researchers, scientists, and drug development professionals.

Troubleshooting Guide: Non-Significant Regression Coefficients

Question:

Answer:

A non-significant regression coefficient (indicated by a p-value > 0.05) suggests that, based on your sample data, you cannot confidently conclude that a relationship exists between the predictor and the outcome variable in the population.[1] There are several potential reasons for this. The following table summarizes the most common causes, how to diagnose them, and potential solutions to address the issue in your experimental analysis.

Potential Cause Diagnosis Potential Solutions
Small Sample Size / Low Statistical Power Perform a post-hoc power analysis. If statistical power is low (typically < 0.8), your study may not have been able to detect a true effect.[2][3]Increase the sample size for future experiments. If the effect size is small, a larger sample will be needed to achieve adequate power.[4][5]
Multicollinearity Calculate the Variance Inflation Factor (VIF) for each predictor. A VIF greater than 5-10 suggests high multicollinearity.[6][7] Examine a correlation matrix of your predictors for high correlation coefficients.Remove one of the highly correlated variables.[8] Combine the correlated variables into a single composite score. Use advanced regression techniques like ridge regression.[8]
Omitted Variable Bias Review existing literature and theory to determine if any key variables are missing from your model. The inclusion of a new, relevant variable may change the significance of others.[9][10][11]Include the omitted variable in your regression model. If the variable cannot be measured, acknowledge this as a limitation or use an instrumental variable approach.[12]
Incorrect Functional Form Plot the residuals of your model against the predicted values. A discernible pattern (e.g., a U-shape) suggests a non-linear relationship.[13]Apply a non-linear transformation to the predictor or outcome variable (e.g., logarithmic, polynomial). Use a non-linear regression model.
Measurement Error Review your data collection protocols. High variability or known inaccuracies in measurement can obscure a true relationship.Improve measurement precision in future experiments. Use statistical methods that account for measurement error, such as errors-in-variables models.
No True Relationship The non-significant result may accurately reflect a lack of a meaningful relationship between the variables.[13]Report the non-significant finding. This is a valid and important result in itself.[14] Focus on other significant predictors in your model.

Frequently Asked Questions (FAQs)

Q1: What does a non-significant p-value truly mean?

A non-significant p-value indicates that the observed data are not sufficient to reject the null hypothesis, which states that the coefficient is zero.[1] It does not prove that there is no effect; it simply means that the evidence from your sample is not strong enough to conclude that an effect exists in the population.[15][16]

Q2: Should I automatically remove non-significant variables from my model?

Not necessarily. There are several reasons to keep a non-significant variable:

  • Confounding: The variable may be an important confounder that needs to be controlled for to get unbiased estimates of other variables. Removing it could introduce omitted variable bias.[9][10]

  • Theoretical Importance: The variable may be central to your hypothesis, and its non-significance is an important finding in itself.[14]

  • Multicollinearity: The variable might be non-significant due to multicollinearity, but its removal could affect the coefficients of other correlated variables.[7][17]

Q3: Can my overall model be significant (significant F-test) even if some individual coefficients are not?

Yes. A significant F-test indicates that your set of independent variables, when taken together, significantly predicts the dependent variable.[18] However, this does not mean every individual predictor is significant. This often occurs when you have a mix of strong and weak predictors, or when multicollinearity is present.[17]

Q4: How large of a sample size do I need to achieve statistical significance?

The required sample size depends on three main factors:

  • Effect Size: The magnitude of the relationship you are trying to detect. Smaller effects require larger samples.

  • Significance Level (alpha): Usually set at 0.05.

  • Statistical Power: The desired probability of detecting a true effect, typically set at 0.80 or higher.[2][3]

You can use a power analysis before conducting your experiment to estimate the necessary sample size.[2][4]

Q5: What is the difference between statistical significance and practical (or clinical) significance?

With a very large sample size, even a tiny, trivial effect can become statistically significant.[19] Practical or clinical significance refers to whether the magnitude of the effect is meaningful in a real-world context. It's crucial to interpret the effect size (i.e., the regression coefficient) in addition to the p-value.[20]

Experimental Protocol Example: Dose-Response Analysis

Objective: To determine the effect of a new compound (Drug-X) on the reduction of a cancer biomarker (Bio-Y) in a preclinical model, while controlling for the initial tumor volume.

Methodology:

  • Experimental Design: 60 subjects are randomly assigned to one of six groups (n=10 per group): a vehicle control group and five groups receiving different doses of Drug-X (10, 20, 30, 40, 50 mg/kg).

  • Data Collection: The initial tumor volume (mm³) is measured at day 0. After 14 days of treatment, the level of Bio-Y in the tumor tissue is quantified.

  • Statistical Model: A multiple linear regression model is used to analyze the data: BioY_Reduction = β₀ + β₁(Dose) + β₂(Initial_Volume) + ε

    • BioY_Reduction: The percentage reduction in biomarker Y.

    • Dose: The dosage of Drug-X in mg/kg.

    • Initial_Volume: The tumor volume at day 0.

Scenario: Non-Significant Result

Upon analysis, the overall model is significant (F-test p < 0.05). The coefficient for Initial_Volume is significant (p = 0.01), but the coefficient for Dose is not (p = 0.12).

Troubleshooting in Context:

  • Check for Power: A post-hoc power analysis is conducted. Given the observed effect size and sample size of 60, the power to detect an effect for the Dose variable was only 0.45. This suggests the study was underpowered.[2][3]

  • Examine Functional Form: A scatter plot of Dose versus the residuals of the model is created. The plot shows a "U" shape, suggesting that the relationship between Dose and BioY_Reduction may not be linear. The effect might plateau or decrease at higher doses.

  • Re-evaluate the Model: Based on the residual plot, a new model with a quadratic term for dose is fitted: BioY_Reduction = β₀ + β₁(Dose) + β₂(Dose²) + β₃(Initial_Volume) + ε

  • Interpret New Results: In the new model, both the Dose and Dose² terms are statistically significant. This indicates a non-linear dose-response relationship, where the effect of the drug changes at different dosage levels.

Visualizations

TroubleshootingWorkflow start Non-Significant Coefficient Found q1 Is the sample size adequate? (Check Power Analysis) start->q1 q2 Is there high multicollinearity? (Check VIF > 5) q1->q2 Yes sol1 Increase sample size in future studies. q1->sol1 No q3 Is the functional form correct? (Check Residual Plots) q2->q3 No sol2 Remove or combine correlated predictors. q2->sol2 Yes q4 Are there omitted variables? (Review Theory) q3->q4 No sol3 Transform variables or use a non-linear model. q3->sol3 Yes sol4 Add relevant variables to the model. q4->sol4 Yes end_node No true effect exists. Report as a valid finding. q4->end_node No

Caption: Troubleshooting workflow for non-significant regression coefficients.

Multicollinearity cluster_predictors Predictor Variables cluster_outcome Outcome Variable X1 Drug A Dose X2 Drug B Dose X1->X2 High Correlation Y Biomarker Level X1->Y Effect of A? X2->Y Effect of B? note The model struggles to distinguish the individual effects of Drug A and Drug B on the biomarker level, potentially leading to non-significant coefficients for both.

Caption: Diagram illustrating the concept of multicollinearity.

PowerAnalysis power Statistical Power sample_size Sample Size sample_size->power Increases effect_size Effect Size effect_size->power Increases alpha Significance Level (α) alpha->power Increases

Caption: Relationship between sample size, effect size, and statistical power.

References

Troubleshooting long execution times for complex regression models.

Author: BenchChem Technical Support Team. Date: December 2025

Technical Support Center: Complex Regression Models

This guide provides troubleshooting steps and frequently asked questions to address long execution times for complex regression models, tailored for professionals in research, science, and drug development.

Frequently Asked Questions (FAQs)

Q1: My regression model is taking an unexpectedly long time to train. What are the most common causes?

A1: Long execution times in complex regression models typically stem from one or more of the following areas:

  • Data-Related Issues :

    • Large Datasets : Processing large volumes of data is inherently time-consuming.

    • High Dimensionality : A high number of features (predictors) increases computational complexity.

    • Inefficient Data Preprocessing : The methods used to clean and prepare data, such as handling missing values or encoding categorical features, can create bottlenecks.[1] For instance, including categorical predictors with a large number of unique values can significantly slow down model training.[2]

  • Model Complexity :

    • Overfitting : Highly complex models that attempt to capture noise in the training data can lead to longer training times and poor generalization.[3][4]

    • Non-Linearity : Modeling complex, non-linear relationships often requires more computationally intensive algorithms.[5][6]

  • Algorithmic and Code Inefficiency :

    • Suboptimal Algorithms : Using an inefficient optimization algorithm for the given data size can drastically increase execution time. For example, standard gradient descent can be slow on large datasets.[7][8]

    • Inefficient Code : The implementation of the model and data processing pipeline may contain performance bottlenecks. Identifying these requires code profiling.[9][10]

  • Hardware Limitations :

    • Insufficient Resources : The available CPU, RAM, or I/O resources may be insufficient for the scale of the problem.

    • Lack of Hardware Acceleration : Not utilizing specialized hardware like Graphics Processing Units (GPUs) or Field-Programmable Gate Arrays (FPGAs) for parallelizable tasks can be a major performance limiter.[11][12]

Q2: How can I identify the specific bottleneck causing the slowdown in my Python code?

A2: The most effective way to pinpoint performance issues in your code is through profiling . Profiling analyzes your code's execution and measures metrics like the time spent in each function or on each line of code.[13] This allows you to identify "hot spots" that are prime candidates for optimization.[9]

Code Profiling Workflow

start Start: Long Execution Time run_profiler 1. Run Profiler (e.g., cProfile, Pyinstrument) start->run_profiler analyze 2. Analyze Results (Identify functions with high cumulative time) run_profiler->analyze identify 3. Identify Bottleneck (e.g., slow data loading, inefficient loop) analyze->identify optimize 4. Optimize Code (Refactor algorithm, vectorize operations) identify->optimize reprofile 5. Re-run Profiler to Verify Improvement optimize->reprofile reprofile->identify Further optimization needed end_node End: Optimized Performance reprofile->end_node

A typical workflow for identifying and fixing code bottlenecks.

Common Python Profiling Tools:

  • cProfile : A built-in deterministic profiler that provides detailed statistics on function calls.[10] It's a good starting point for a general overview.

  • line_profiler : A third-party tool that measures the execution time of each individual line of code within a function, offering more granularity.[14]

  • Pyinstrument : A statistical profiler that samples the call stack at intervals, which results in lower overhead and can make it easier to spot the most time-consuming parts of your code.[9][14]

Q3: Can changing my optimization algorithm improve speed?

A3: Yes, significantly. The choice of optimization algorithm is critical, especially with large datasets.[15] For many regression problems, iterative methods like gradient descent are used to minimize the error.[15]

  • Batch Gradient Descent : Calculates the gradient using the entire dataset. This is computationally expensive and slow for large datasets.

  • Stochastic Gradient Descent (SGD) : Updates the model parameters using only a single data sample at a time. This is much faster and can be parallelized.[7]

  • Mini-Batch Gradient Descent : Strikes a balance by updating parameters using a small, random subset (a "mini-batch") of the data. This approach leverages hardware optimizations for matrix operations and enables parallel processing, offering a good trade-off between computational efficiency and accuracy.[16]

Q4: What is regularization and can it help with long execution times?

A4: Regularization is a set of techniques used to prevent overfitting by adding a penalty term to the model's objective function, which discourages excessive complexity.[3][17] While its primary goal is to improve model generalization, it can indirectly reduce execution time by promoting simpler models.[18]

  • L1 Regularization (Lasso) : Adds a penalty equal to the absolute value of the coefficients. A key feature is its ability to shrink some coefficients to exactly zero, effectively performing feature selection.[3][18] By creating a sparser model that uses fewer features, it can reduce computational complexity and training time.[19]

  • L2 Regularization (Ridge) : Adds a penalty equal to the square of the magnitude of the coefficients. It shrinks coefficients but does not set them to zero.[18][20] This is particularly useful for handling multicollinearity (high correlation between predictor variables).[18][21]

Troubleshooting Guides

Guide 1: Optimizing the Data Preprocessing Pipeline

If profiling reveals that a significant amount of time is spent on data preparation, consider the following steps. Poor data preprocessing can severely impact model performance.[1]

Initial Troubleshooting Workflow

start Long Execution Time Detected profile Profile Code start->profile is_data Is Data Preprocessing a Bottleneck? profile->is_data is_model Is Model Training a Bottleneck? is_data->is_model No data_guide Go to Data Optimization Guide is_data->data_guide Yes is_code Is Custom Code Inefficient? is_model->is_code No model_guide Go to Algorithmic Optimization Guide is_model->model_guide Yes hardware_guide Go to Parallelization & Hardware Guide is_code->hardware_guide Yes/No (Consider for all cases)

A high-level troubleshooting decision workflow.

  • Handling Missing Values :

    • Problem : Simple imputation methods (e.g., mean, median) might be fast, but more complex methods like model-based imputation can be slow.

    • Solution : For very large datasets, consider removing rows with missing values if they constitute a small fraction of the total data.[22] Alternatively, use faster imputation techniques or libraries optimized for this task.

  • Encoding Categorical Variables :

    • Problem : One-hot encoding can create a very wide and sparse dataset if a categorical variable has many unique values, increasing memory usage and computation time.[2][23]

    • Solution : If there is an ordinal relationship, use Label Encoding, which converts categories to a single column of numbers.[22] For high-cardinality features, consider grouping less frequent categories into a single "other" category.[2]

  • Feature Scaling :

    • Problem : Numerical features with vastly different scales can cause some optimization algorithms to converge slowly.[2]

    • Solution : Apply standardization (scaling to a mean of 0 and standard deviation of 1) or normalization (scaling to a range of[24]).[23] This is often a quick step with a significant impact on convergence speed.

  • Outlier Detection :

    • Problem : Outliers can disproportionately influence the model, and complex detection methods can be slow.[21]

    • Solution : Use statistically efficient methods like Z-score or Interquartile Range (IQR) to identify outliers.[23] Consider using robust regression models that are less sensitive to outliers.

Guide 2: Leveraging Parallel Computing and Hardware Acceleration

When your model or dataset is too large for a single machine to process efficiently, you should consider parallel and distributed computing.[24]

Parallel Computing Strategies

cluster_data Data Parallelism cluster_model Model Parallelism d_data Full Dataset d_split Split Data d_data->d_split d_w1 Worker 1 (Model A, Data 1) d_split->d_w1 d_w2 Worker 2 (Model A, Data 2) d_split->d_w2 d_w3 Worker N (Model A, Data N) d_split->d_w3 d_agg Aggregate Results d_w1->d_agg d_w2->d_agg d_w3->d_agg m_data Full Dataset m_w1 Worker 1 (Model Part 1) m_data->m_w1 m_w2 Worker 2 (Model Part 2) m_w1->m_w2 m_w3 Worker N (Model Part N) m_w2->m_w3

Data parallelism vs. Model parallelism.

  • Data Parallelism : The dataset is split into smaller chunks, and a complete copy of the model is trained on each chunk in parallel across multiple cores or machines.[24] This is the most common approach and is effective when the dataset is large but the model fits on a single machine.

  • Model Parallelism : The model itself is split across different machines.[24] This strategy is used when the model is too large to fit into the memory of a single worker, which can occur with very deep neural networks.

Hardware Acceleration : Many regression calculations, especially those involving large matrices, can be significantly sped up by specialized hardware.

  • GPUs : Highly effective for the parallel computations required by many machine learning algorithms.

  • FPGAs and ASICs : Offer even greater performance and energy efficiency for specific, customized tasks and are increasingly used in large-scale machine learning deployments.[12][25]

Quantitative Data and Experimental Protocols

Table 1: Performance of Parallel Gradient Descent

This table summarizes the results of an experiment investigating the parallelization of gradient descent for regression analysis on large datasets.

Technology UsedNumber of Cores/ThreadsAchieved Speedup
OpenMP & MPI6~5x

Experimental Protocol : The study focused on parallelizing the gradient descent and stochastic gradient descent algorithms using OpenMP and MPI technologies.[8] The efficiency of the parallel algorithms was tested on a personal computer with a six-core processor.[8] Performance was measured by varying the number of threads and processor cores to analyze the acceleration achieved compared to a sequential implementation.[8]

Table 2: Hardware Accelerator Performance Comparison

This table shows the results of a study comparing different hardware platforms for accelerating sparse matrix multiplication, a common operation in complex models.

Hardware PlatformRelative Speedup (vs. CPU)
Intel i5-5257U CPU (2.7 GHz)1x (Baseline)
NVIDIA Jetson TX2 GPU~5.5x
Xilinx Alveo U200 FPGA11x

Experimental Protocol : A framework for accelerating sparse matrix multiplication was implemented on three different hardware platforms: a standard CPU, an embedded GPU, and an FPGA.[11][26] The latency and throughput of each implementation were measured to compare their performance. The FPGA platform demonstrated a 2x speedup over the GPU and an 11x speedup over the CPU.[11][26]

Table 3: Model Performance in Predicting Drug-Drug Interactions

This table compares the performance of three different regression-based machine learning models for predicting changes in drug exposure caused by pharmacokinetic drug-drug interactions.

Machine Learning ModelR² (Coefficient of Determination)Root Mean Square Error (RMSE)% Predictions within 2-fold Error
Random Forest~0.50~0.3069%
Elastic Net~0.55~0.2875%
Support Vector Regressor (SVR)~0.60~0.2578%

Experimental Protocol : The study used a dataset from 120 clinical drug-drug interaction studies.[27] Features included drug structure, physicochemical properties, and in vitro pharmacokinetic properties.[27] Three regression models—Random Forest, Elastic Net, and SVR—were trained and evaluated using fivefold cross-validation to predict the fold change in drug exposure.[27] The SVR model showed the strongest predictive performance.[27]

References

Technical Support Center: Regression Analysis Troubleshooting

Author: BenchChem Technical Support Team. Date: December 2025

This guide provides troubleshooting steps and answers to frequently asked questions for researchers, scientists, and drug development professionals who encounter issues with regression models where all coefficients are either NaN (Not a Number) or zero.

Frequently Asked Questions (FAQs)

Q1: Why are all my regression coefficients NaN?

When all regression coefficients in your model are NaN, it indicates a fundamental issue with the input data or the model specification that makes it impossible to compute valid coefficients. This is often due to one of the following reasons:

  • Missing Data: The presence of NaN values in your dataset is a common cause. Most regression algorithms cannot handle missing data and will output NaN if they are present in either the dependent or independent variables.[1][2][3][4]

  • Perfect Multicollinearity: This occurs when one independent variable is a perfect linear combination of one or more other independent variables.[2][5][6] For example, including the same measurement in different units (e.g., temperature in both Celsius and Fahrenheit). In this situation, the model cannot determine the unique contribution of each collinear variable, leading to NaN coefficients.[6][7]

  • Zero Variance in a Predictor: If an independent variable has no variability (i.e., all its values are the same), it is impossible to estimate its relationship with the dependent variable, which can result in NaN coefficients.[2][5]

  • Insufficient Data: If the number of data points is less than the number of coefficients to be estimated (including the intercept), the system is underdetermined, and a unique solution cannot be found.[2][6][8]

Q2: What should I do if all my regression coefficients are NaN?

Follow these troubleshooting steps to identify and resolve the issue:

  • Inspect for Missing Values: Carefully examine your dataset for any missing values (NaNs).[1][2] Most software packages have functions to detect and count missing values. If found, you need to decide on a strategy to handle them, such as removing the rows with missing data or imputing the missing values using methods like mean, median, or more advanced techniques like MICE (Multiple Imputation by Chained Equations).[3][9]

  • Check for Multicollinearity: Analyze the correlation between your independent variables. A high correlation between two or more variables might indicate multicollinearity. A more formal way to check for this is to calculate the Variance Inflation Factor (VIF) for each predictor. A VIF greater than 5 or 10 is often considered problematic.[5]

  • Examine Predictor Variance: For each independent variable, calculate the variance to ensure it is not zero. If a variable has zero variance, it should be removed from the model.[5]

  • Ensure Sufficient Data: Verify that you have more observations (data points) than the number of predictors in your model.[8]

Q3: Why are all my regression coefficients zero?

Observing all zero coefficients can be perplexing but is often explainable by the following:

  • No Relationship: It's possible that there is no linear relationship between the independent variables and the dependent variable in your dataset.[10]

  • Regularization: If you are using a regularization technique like Lasso (L1 regularization), the penalty term can shrink the coefficients of less important features to exactly zero.[11] This is a form of automatic feature selection. If all coefficients are zero, the regularization parameter (lambda or alpha) might be too high.[12][13]

  • Data Scaling Issues: A very large range in one or more independent variables can sometimes lead to numerical precision problems, causing coefficients to be estimated as zero.[5][14]

  • Perfect Fit: In rare cases, if the model perfectly predicts the dependent variable, the residual sum of squares (RSS) will be zero, which can lead to zero coefficients and their standard errors.[10]

Q4: How can I troubleshoot a model with all zero coefficients?

Here are the steps to take when your model yields all zero coefficients:

  • Review Your Model Choice: If you are using a regularized regression model like Lasso, try reducing the regularization parameter (alpha or lambda).[13] You might also consider using a different model, such as Ridge regression (L2 regularization), which shrinks coefficients towards zero but rarely sets them exactly to zero.[11]

  • Scale Your Features: Standardize or normalize your independent variables to have a similar scale. This can help with numerical stability and improve the performance of some regression algorithms.[5][14]

  • Investigate Variable Relationships: Use scatter plots and correlation analysis to visually inspect the relationships between your independent variables and the dependent variable. This can help you determine if a linear relationship is a reasonable assumption.

  • Consider Non-Linear Models: If there is no apparent linear relationship, you may need to explore non-linear regression models or transform your variables.[10]

Troubleshooting Summary

Issue Potential Causes Recommended Solutions
All Coefficients are NaN1. Missing data in the dataset.[1][2][4] 2. Perfect multicollinearity among predictors.[5][6][7] 3. An independent variable has zero variance.[2][5] 4. Fewer data points than predictors.[6][8]1. Remove or impute missing values.[3][9] 2. Identify and remove one of the collinear variables or combine them. Check VIFs.[5] 3. Remove the constant variable from the model. 4. Collect more data or reduce the number of predictors.
All Coefficients are 01. No actual linear relationship exists.[10] 2. The regularization parameter (e.g., in Lasso) is too high.[12][13] 3. Large differences in the scale of predictors.[5][14] 4. The model achieves a perfect fit.[10]1. Explore non-linear models or variable transformations.[10] 2. Reduce the regularization parameter or use a different regularization method.[11] 3. Standardize or normalize the independent variables.[5] 4. Verify the data and model for potential data leakage or trivial relationships.

Hypothetical Experimental Protocol

Objective: To build a predictive model for drug efficacy based on genomic and proteomic markers.

Methodology:

  • Data Collection:

    • Dependent Variable (Y): Drug efficacy measured as a continuous variable (e.g., percentage of cancer cell death).

    • Independent Variables (X):

      • Gene expression levels of 10 specific genes (Gene_1 to Gene_10) obtained from microarray analysis.

      • Protein expression levels of 5 key proteins (Protein_A to Protein_E) measured by mass spectrometry.

      • A categorical variable indicating the cell line used (Cell_Line_X, Cell_Line_Y, Cell_Line_Z).

  • Data Preprocessing:

    • Handling Missing Values: Any missing values in the gene or protein expression data were imputed using the mean of the respective feature.

    • Categorical Variable Encoding: The 'Cell_Line' variable was one-hot encoded, creating three new binary variables.

    • Data Splitting: The dataset was randomly split into a training set (80%) and a testing set (20%).

    • Feature Scaling: All independent variables were standardized to have a mean of 0 and a standard deviation of 1.

  • Model Training:

    • A multiple linear regression model was initially fitted to the training data.

    • Due to the high number of features, a Lasso regression model was also trained to perform feature selection and reduce model complexity.

Potential for NaN/Zero Coefficients in this Protocol:

  • NaN Coefficients: If, for instance, Gene_3 was a perfect linear combination of Gene_1 and Gene_2 (e.g., Gene_3 = 2 * Gene_1 + 0.5 * Gene_2), this perfect multicollinearity would result in NaN coefficients for these variables. Similarly, if one of the one-hot encoded cell line variables had no observations in the training set (zero variance), it would also cause issues.

  • Zero Coefficients: When applying the Lasso regression, if the regularization parameter (alpha) was set too high, it could shrink the coefficients of all genes and proteins to zero, suggesting that with that level of penalty, none of the features are considered important for predicting drug efficacy.

Visual Troubleshooting Guide

Troubleshooting_Regression_Coefficients start Start: All Regression Coefficients are NaN or 0 check_type Are coefficients NaN or 0? start->check_type check_missing Check for Missing Data (NaNs) in Dataset check_type->check_missing NaN check_regularization Using Regularized Regression (e.g., Lasso)? check_type->check_regularization Zero nan_path NaN handle_missing Impute or Remove Missing Data check_missing->handle_missing Found check_multicollinearity Check for Perfect Multicollinearity (VIF) check_missing->check_multicollinearity Not Found handle_missing->check_multicollinearity handle_multicollinearity Remove Collinear Variables check_multicollinearity->handle_multicollinearity Found check_variance Check for Zero Variance Predictors check_multicollinearity->check_variance Not Found handle_multicollinearity->check_variance handle_variance Remove Zero Variance Predictors check_variance->handle_variance Found check_data_size Check if Observations > Predictors check_variance->check_data_size Not Found handle_variance->check_data_size handle_data_size Collect More Data or Reduce Predictors check_data_size->handle_data_size No end_node Re-run Regression and Evaluate check_data_size->end_node Yes handle_data_size->end_node zero_path Zero adjust_lambda Lower Regularization Parameter (alpha/lambda) check_regularization->adjust_lambda Yes check_scaling Check Feature Scaling check_regularization->check_scaling No yes_regularization Yes no_regularization No adjust_lambda->end_node scale_features Standardize or Normalize Features check_scaling->scale_features Not Scaled check_relationships Investigate Variable Relationships check_scaling->check_relationships Scaled scale_features->check_relationships consider_nonlinear Consider Non-Linear Models or Transformations check_relationships->consider_nonlinear No Linear Relationship check_relationships->end_node Linear Relationship Possible consider_nonlinear->end_node

Caption: Troubleshooting workflow for NaN or zero regression coefficients.

Signaling Pathway Analysis Example

In drug development, regression can be used to model the relationship between the inhibition of a signaling pathway and a cellular response.

Signaling_Pathway cluster_input Pathway Components (Predictors) cluster_output Cellular Response (Dependent Variable) Drug Drug Concentration Kinase_A Kinase A Activity Drug->Kinase_A inhibits Phospho_B Phospho-Protein B Kinase_A->Phospho_B phosphorylates Gene_C Gene C Expression Phospho_B->Gene_C regulates Apoptosis Apoptosis Level Gene_C->Apoptosis induces

Caption: Hypothetical signaling pathway for regression analysis.

References

Validation & Comparative

A Researcher's Guide to Validating Multiple Regression Models

Author: BenchChem Technical Support Team. Date: December 2025

The process of validating a multiple regression model ensures that the model is not only a good fit for the data used to create it, but that it is also generalizable to new data.[1][2] This involves checking the model's assumptions, assessing its goodness of fit, and evaluating its predictive power.[3] The three primary methods for this validation are residual analysis, goodness-of-fit statistics, and cross-validation.

Comparative Overview of Validation Techniques

To aid in selecting the most appropriate validation strategy, the following table summarizes the key techniques, their primary purpose, and their main advantages and disadvantages.

Validation TechniquePrimary PurposeKey Metrics/PlotsAdvantagesDisadvantages
Residual Analysis To check if the assumptions of linear regression are met.[4][5]Residual plots, Q-Q plots, Cook's D.[4][6]Provides detailed diagnostic information about the model's fit and potential issues like non-linearity and outliers.[3][5]Can be subjective and requires careful interpretation of plots.
Goodness-of-Fit Statistics To quantify how well the model fits the sample data.[7]R-squared (R²), Adjusted R-squared, Standard Error of the Regression (S).[8]Provides a quick and easy-to-understand measure of the proportion of variance explained by the model.[7][9]R² can be misleadingly high, and a high R² does not guarantee the model is good.[3]
Cross-Validation To assess the model's ability to generalize to new, unseen data and to avoid overfitting.[10][11]Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE).[2][12]Provides a more robust estimate of the model's performance on new data.[10][13]Can be computationally intensive, especially for large datasets.[14]

In-Depth Methodologies and Experimental Protocols

Residual Analysis

Residual analysis is a critical step to verify that the assumptions of multiple linear regression are met.[4] The residuals are the differences between the observed values and the values predicted by the model.[5][15]

Experimental Protocol:

  • Fit the Multiple Regression Model: Develop the regression model using your dataset.

  • Calculate Residuals: For each data point, calculate the residual by subtracting the predicted value from the actual observed value.

  • Generate Residual Plots:

    • Residuals vs. Predicted Values: This is the most important plot. It helps to check for:

      • Linearity: The points should be randomly scattered around the horizontal line at zero.[4] A curved pattern suggests a non-linear relationship.[4]

      • Homoscedasticity (Constant Variance): The spread of the residuals should be roughly the same across all predicted values. A funnel shape indicates heteroscedasticity (non-constant variance).[16]

    • Normal Q-Q Plot of Residuals: This plot is used to check the normality assumption of the residuals.[4] The points should fall approximately along the straight diagonal line.[16]

  • Identify Outliers and Influential Points: Use metrics like Cook's D to identify data points that may have an undue influence on the model.[6] A Cook's D value greater than 1 is generally considered to indicate an influential point.[6]

Goodness-of-Fit Statistics

These statistics provide a quantitative measure of how well the regression model fits the observed data.

Experimental Protocol:

  • Calculate R-squared (R²): This value represents the proportion of the variance in the dependent variable that is predictable from the independent variables.[7][9] It ranges from 0 to 1, with higher values indicating a better fit.[9]

  • Calculate Adjusted R-squared: This is a modified version of R² that accounts for the number of predictors in the model.[17] It is generally a more accurate measure of model fit, as it penalizes the inclusion of unnecessary variables.

  • Calculate the Standard Error of the Regression (S): This statistic measures the typical distance between the observed values and the regression line.[8] A smaller S value indicates that the data points are closer to the fitted line.

Cross-Validation

Cross-validation is a powerful technique for assessing how the results of a statistical analysis will generalize to an independent dataset.[10][13] It is particularly useful for guarding against overfitting.[11]

Experimental Protocol:

  • Data Splitting (Hold-out Method):

    • Randomly divide your dataset into a training set (e.g., 80% of the data) and a testing set (e.g., 20% of the data).[14]

    • Fit the multiple regression model using the training set.

    • Use the fitted model to make predictions on the testing set.

    • Calculate the prediction error using metrics like Mean Squared Error (MSE), Root Mean Squared Error (RMSE), or Mean Absolute Error (MAE).[2][12]

  • K-Fold Cross-Validation:

    • Randomly divide the dataset into k equal-sized subsets (or "folds").[10] A common choice for k is 5 or 10.[18]

    • For each of the k folds:

      • Use the fold as a validation set and the remaining k-1 folds as a training set.

      • Fit the model on the training set and evaluate it on the validation set.

      • Record the evaluation score (e.g., MSE).

    • The performance of the model is the average of the scores from the k folds.[10]

  • Leave-One-Out Cross-Validation (LOOCV):

    • This is a special case of k-fold cross-validation where k is equal to the number of observations in the dataset.[14]

    • For each observation:

      • Use that single observation as the validation set and the remaining observations as the training set.

      • Fit the model and calculate the prediction error.

    • The final performance is the average of these errors. While thorough, this method can be computationally expensive.[1][14]

Visualizing the Validation Workflow

The following diagram illustrates the logical flow of the multiple regression model validation process, from initial model fitting to the final assessment of its validity.

Multiple Regression Validation Workflow cluster_0 Model Building cluster_1 Model Validation cluster_2 Assessment cluster_3 Decision start Start with Dataset fit_model Fit Multiple Regression Model start->fit_model residual_analysis Residual Analysis fit_model->residual_analysis goodness_of_fit Goodness-of-Fit Statistics fit_model->goodness_of_fit cross_validation Cross-Validation fit_model->cross_validation check_assumptions Check Assumptions (Linearity, Normality, etc.) residual_analysis->check_assumptions quantify_fit Quantify In-Sample Fit (R², Adjusted R²) goodness_of_fit->quantify_fit assess_generalizability Assess Generalizability (MSE, RMSE) cross_validation->assess_generalizability model_valid Model is Valid check_assumptions->model_valid Assumptions Met model_invalid Model is Invalid (Refine Model) check_assumptions->model_invalid Assumptions Violated quantify_fit->model_valid Good Fit quantify_fit->model_invalid Poor Fit assess_generalizability->model_valid Good Predictive Power assess_generalizability->model_invalid Poor Predictive Power model_invalid->fit_model Iterate

Caption: Workflow for validating a multiple regression model.

References

A Comparative Guide to Holdout Sampling for Regression Model Validation

Author: BenchChem Technical Support Team. Date: December 2025

In the landscape of predictive modeling, particularly within scientific research and drug development, the rigorous validation of regression models is paramount to ensure their accuracy, reliability, and generalizability. One of the fundamental techniques for this validation is the use of a holdout sample. This guide provides an objective comparison of the holdout method with its primary alternative, k-fold cross-validation, supported by experimental data and detailed protocols to inform researchers, scientists, and drug development professionals in their model validation strategies.

The Holdout Method: A Foundational Approach

The holdout method is a straightforward and computationally efficient technique for validating a regression model.[1] It involves partitioning the dataset into two distinct, mutually exclusive subsets: a training set and a testing or holdout set.

The process is as follows:

  • Data Split: The available data is divided, often with a 70/30 or 80/20 split, where the larger portion is allocated for training the model and the smaller portion is held out for testing.[1]

  • Model Training: The regression model is trained exclusively on the training dataset.

  • Performance Evaluation: The trained model is then used to make predictions on the holdout set, which it has not seen before. The performance of the model is assessed by comparing its predictions to the actual known values in the holdout set, using metrics such as Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and R-squared (R²).[1]

The primary purpose of this approach is to obtain an unbiased estimate of how the model will perform on new, unseen data, thereby helping to identify issues like overfitting, where a model performs well on the data it was trained on but fails to generalize to new data.

An Alternative Approach: K-Fold Cross-Validation

A widely recognized and often preferred alternative to the holdout method is k-fold cross-validation. This technique is designed to provide a more robust and less biased estimate of model performance, especially when dealing with limited datasets.

The k-fold cross-validation process is more involved:

  • Data Partitioning: The dataset is randomly divided into 'k' equal-sized subsets, or "folds".

  • Iterative Training and Testing: The model is trained 'k' times. In each iteration, a different fold is held out as the test set, while the remaining 'k-1' folds are used for training.

  • Performance Aggregation: The performance metric (e.g., MSE) is calculated for each of the 'k' iterations. The final performance of the model is the average of these 'k' metrics.

This method ensures that every data point is used for both training and testing, which can lead to a more reliable assessment of the model's generalization capabilities.

Workflow Comparison

To visualize the logical flow of these two validation methods, the following diagrams are provided.

holdout_workflow cluster_data Dataset cluster_split Data Splitting cluster_subsets Subsets cluster_modeling Modeling & Evaluation raw_data Full Dataset split Split (e.g., 80/20) raw_data->split training_data Training Set split->training_data holdout_data Holdout Set split->holdout_data train_model Train Model training_data->train_model evaluate_model Evaluate Performance holdout_data->evaluate_model train_model->evaluate_model

Holdout Method Workflow

kfold_workflow cluster_data Dataset cluster_split Data Partitioning cluster_iteration Iterative Process (k times) cluster_evaluation Performance Aggregation raw_data Full Dataset split Split into k Folds raw_data->split iteration For each Fold i in k: - Train on k-1 Folds - Test on Fold i split->iteration average Average Performance Metrics iteration->average

K-Fold Cross-Validation Workflow

Quantitative Comparison: A Simulation Study

To provide a quantitative comparison of the holdout and k-fold cross-validation methods, we refer to a simulation study designed to assess the performance of a regression model under different validation schemes.

Experimental Protocol

Objective: To compare the performance of a multiple linear regression model when validated using the holdout method versus 10-fold cross-validation.

Dataset: A simulated dataset was generated with 500 observations. The dataset includes a continuous dependent variable and five independent variables with varying degrees of correlation with the dependent variable.

Model: A standard multiple linear regression model was used to predict the dependent variable based on the five independent variables.

Validation Procedures:

  • Holdout Method: The dataset was randomly split into a training set (80% of the data, 400 observations) and a holdout set (20% of the data, 100 observations). The regression model was trained on the training set and evaluated on the holdout set. This process was repeated 100 times with different random splits to assess the variability of the performance estimates.

  • 10-Fold Cross-Validation: The entire dataset of 500 observations was used. The data was divided into 10 folds of 50 observations each. The model was trained and evaluated 10 times, with each fold serving as the test set once. The performance metrics were then averaged across the 10 folds.

Performance Metrics:

  • R-squared (R²): The proportion of the variance in the dependent variable that is predictable from the independent variables.

  • Mean Squared Error (MSE): The average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value.

Experimental Results

The following table summarizes the performance of the regression model under the two validation methods. For the holdout method, the average and standard deviation of the performance metrics over the 100 repetitions are reported.

Validation MethodR-squared (R²)Mean Squared Error (MSE)
Holdout Method (80/20 split) 0.70 (± 0.07)0.30 (± 0.08)
10-Fold Cross-Validation 0.730.27

Discussion and Recommendations

The results of the simulation study indicate that 10-fold cross-validation yielded a higher average R-squared and a lower average MSE compared to the holdout method. More importantly, the holdout method exhibited a higher variance in its performance estimates, as indicated by the standard deviation across multiple splits. This suggests that the performance metrics obtained from a single holdout split can be highly dependent on the specific data points that end up in the training and testing sets.

The choice between the holdout method and k-fold cross-validation depends on several factors, including the size of the dataset and the available computational resources.

FeatureHoldout MethodK-Fold Cross-Validation
Computational Cost Low (model is trained once)High (model is trained k times)
Data Usage Inefficient (a portion of data is not used for training)Efficient (all data is used for training and testing)
Variance of Performance Estimate High (dependent on a single split)Low (averaged over multiple splits)
Bias of Performance Estimate Can be pessimistic (trained on a smaller dataset)Less biased
Recommended Use Case Very large datasets where computational cost is a concern.Smaller datasets where maximizing the use of data is crucial for a robust evaluation.

References

Cross-validation techniques for assessing regression model accuracy.

Author: BenchChem Technical Support Team. Date: December 2025

In the pursuit of robust and reliable regression models for scientific research and drug development, rigorous validation is not merely a best practice—it is a necessity. Cross-validation stands out as a powerful set of techniques to assess a model's predictive accuracy and its ability to generalize to new, unseen data. This guide provides a comparative overview of key cross-validation methods, supported by experimental data and detailed protocols, to aid researchers in selecting and implementing the most appropriate strategy for their regression tasks.

Comparing Cross-Validation Techniques: A Quantitative Overview

The choice of a cross-validation technique can significantly impact the evaluation of a regression model. The following table summarizes the performance of common cross-validation methods based on metrics from a study on Quantitative Structure-Activity Relationship (QSAR) modeling for predicting acute toxicity.[1] The performance of various modeling methods was assessed using different cross-validation protocols, and key metrics such as the coefficient of determination (r²) and the cross-validated coefficient of determination (Q²) were reported.[1]

Cross-Validation TechniqueKey CharacteristicsAdvantagesDisadvantagesTypical Performance (QSAR Toxicity Prediction)[1]
k-Fold Cross-Validation The dataset is randomly partitioned into 'k' equal-sized folds. The model is trained on k-1 folds and validated on the remaining fold, repeated k times.[2]Computationally efficient, provides a good balance between bias and variance.[2]Performance can vary depending on the random splits.For Partial Least Squares (PLS) regression, r² values were consistently high, while Q² values were slightly lower, indicating good but slightly less robust predictive performance compared to the training data.
Leave-One-Out (LOOCV) A special case of k-fold CV where k equals the number of data points. Each data point is used once as the test set.[3]Utilizes the maximum amount of data for training in each iteration, leading to a less biased estimate of the test error.Computationally very expensive for large datasets, can have high variance.[4]For Multiple Linear Regression (MLR), LOOCV often resulted in a larger gap between r² and Q², suggesting a higher risk of overfitting.[1]
Stratified k-Fold Cross-Validation A variation of k-fold where each fold contains approximately the same percentage of samples of each target class (for classification) or a similar distribution of the outcome variable (for regression).Ensures that each fold is a good representative of the whole dataset, which is particularly useful for imbalanced datasets.Can be more complex to implement than standard k-fold.In regression tasks, it helps in ensuring that the mean response value is approximately equal in all folds.[5]
Monte Carlo Cross-Validation (Repeated Random Sub-sampling) The dataset is randomly split into a training and a validation set multiple times.The number of iterations and the size of the splits are not dependent on the number of folds, offering more flexibility.Some data points may be selected more than once in the validation set while others may not be selected at all.This method can provide a robust estimate of the model's performance by averaging the results over multiple random splits.[6]

Experimental Protocols: A Step-by-Step Guide

To ensure reproducibility and consistency in model evaluation, it is crucial to follow a well-defined experimental protocol. Below are detailed methodologies for implementing the discussed cross-validation techniques.

Protocol 1: k-Fold Cross-Validation

  • Data Preparation: Ensure the dataset is clean, pre-processed, and ready for modeling. This includes handling missing values and feature scaling.

  • Partitioning: Randomly shuffle the dataset and divide it into k equal-sized folds. A common choice for k is 5 or 10.[2]

  • Iteration: For each of the k folds: a. Select the current fold as the validation set. b. Use the remaining k-1 folds as the training set. c. Train the regression model on the training set. d. Evaluate the model's performance on the validation set using metrics such as Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and R-squared (R²).[5][7][8] e. Store the performance metrics for the current fold.

  • Performance Aggregation: Calculate the average of the performance metrics across all k folds to obtain a single, robust estimate of the model's accuracy.

Protocol 2: Leave-One-Out Cross-Validation (LOOCV)

  • Data Preparation: As with k-fold, prepare the dataset for modeling.

  • Iteration: For each data point i in the dataset (from 1 to n, where n is the total number of data points): a. Select data point i as the validation set. b. Use the remaining n-1 data points as the training set. c. Train the regression model on the training set. d. Predict the value for the validation data point i. e. Calculate the prediction error (e.g., squared error) for this data point.

  • Performance Aggregation: Calculate the mean of the prediction errors across all n iterations to get the final performance estimate (e.g., MSE).

Protocol 3: Monte Carlo Cross-Validation

  • Data Preparation: Prepare the dataset for modeling.

  • Define Parameters: Determine the number of iterations (N) and the proportion of data to be used for the training set (e.g., 80%).

  • Iteration: For each iteration from 1 to N: a. Randomly split the dataset into a training set and a validation set based on the predefined proportion. b. Train the regression model on the training set. c. Evaluate the model's performance on the validation set using the chosen metrics. d. Store the performance metrics for the current iteration.

  • Performance Aggregation: Average the performance metrics over all N iterations to obtain a stable estimate of the model's performance.

Visualizing Cross-Validation Workflows

To further clarify the logical flow of these techniques, the following diagrams illustrate the process for each cross-validation method.

CrossValidationWorkflows cluster_kfold k-Fold Cross-Validation cluster_loocv Leave-One-Out Cross-Validation cluster_mc Monte Carlo Cross-Validation k_start Start with Dataset k_split Split into k Folds k_start->k_split k_loop_start For each Fold i in k k_split->k_loop_start k_train Train on k-1 Folds k_loop_start->k_train k_validate Validate on Fold i k_train->k_validate k_store Store Performance k_validate->k_store k_loop_end Next i k_store->k_loop_end k_loop_end->k_loop_start more folds k_aggregate Aggregate Results k_loop_end->k_aggregate no more folds k_end Final Performance k_aggregate->k_end l_start Start with Dataset (n points) l_loop_start For each Point i in n l_start->l_loop_start l_train Train on n-1 Points l_loop_start->l_train l_validate Validate on Point i l_train->l_validate l_store Store Error l_validate->l_store l_loop_end Next i l_store->l_loop_end l_loop_end->l_loop_start more points l_aggregate Aggregate Errors l_loop_end->l_aggregate no more points l_end Final Performance l_aggregate->l_end m_start Start with Dataset m_loop_start For each Iteration i in N m_start->m_loop_start m_split Randomly Split into Train and Validation Sets m_loop_start->m_split m_train Train on Train Set m_split->m_train m_validate Validate on Validation Set m_train->m_validate m_store Store Performance m_validate->m_store m_loop_end Next i m_store->m_loop_end m_loop_end->m_loop_start more iterations m_aggregate Aggregate Results m_loop_end->m_aggregate no more iterations m_end Final Performance m_aggregate->m_end

Caption: Workflows of k-Fold, LOOCV, and Monte Carlo cross-validation techniques.

By carefully selecting and implementing an appropriate cross-validation strategy, researchers in drug development and other scientific fields can gain greater confidence in their regression models, leading to more accurate predictions and more impactful discoveries.

References

A Researcher's Guide to Comparing Nested Regression Models Using the F-Test

Author: BenchChem Technical Support Team. Date: December 2025

In statistical modeling, particularly within drug development and scientific research, the principle of parsimony is paramount. We aim for the simplest model that adequately explains the data. When comparing two regression models where one is a simplified version of the other, the F-test for nested models serves as a crucial tool for statistical decision-making.[1][2][3] This guide provides a comprehensive overview of this method, its underlying principles, and a step-by-step protocol for its application.

A nested model is one whose parameters are a subset of a more complex, "full" model.[1][3] The F-test determines whether the additional parameters in the full model provide a statistically significant improvement in fit over the simpler, "reduced" model.[1][2][3] Essentially, it tests the null hypothesis that the coefficients of the additional variables in the full model are all equal to zero.[1][4]

Key Concepts and Formulae

The F-test compares the models by evaluating the reduction in the Residual Sum of Squares (RSS), which is the sum of the squared differences between the observed and predicted values.[2][4] A smaller RSS indicates a better model fit. The F-statistic quantifies whether the reduction in RSS from the reduced to the full model is significant enough to justify the inclusion of additional parameters.[2]

ComponentDescriptionFormula
Full Model The more complex model with additional parameters. Also known as the unrestricted model.[5]Y = β₀ + β₁X₁ + ... + βₖXₖ + ε
Reduced Model The simpler model, which is a special case of the full model with some parameters set to zero.[3][5]Y = β₀ + β₁X₁ + ... + βₚXₚ + ε (where p < k)
Residual Sum of Squares (RSS) Measures the discrepancy between the data and the estimation model.RSS = Σ(yᵢ - ŷᵢ)²
F-Statistic The test statistic for comparing the nested models.[1][2]F = [(RSSᵣ - RSSբ) / (k - p)] / [RSSբ / (n - k)]
Degrees of Freedom (numerator) The number of additional parameters in the full model.[4]df₁ = k - p
Degrees of Freedom (denominator) The degrees of freedom of the full model.[4][6]df₂ = n - k
Variablesn = number of observations, k = number of parameters in the full model, p = number of parameters in the reduced model, RSSᵣ = RSS of the reduced model, RSSբ = RSS of the full model.

Experimental Protocol for F-Test Comparison

Here is a detailed methodology for conducting an F-test to compare nested regression models.

  • Define the Nested Models :

    • Full Model : Specify the comprehensive regression equation that includes all potential explanatory variables.

    • Reduced Model : Specify the simpler model, which omits one or more variables from the full model. The variables in the reduced model must be a subset of the full model.[1][3]

  • State the Hypotheses :

    • Null Hypothesis (H₀) : The additional parameters in the full model are all equal to zero. This implies the reduced model is sufficient.[1][4][7]

    • Alternative Hypothesis (H₁) : At least one of the additional parameters in the full model is not zero. This suggests the full model provides a significantly better fit.[1][4]

  • Fit the Models :

    • Fit the full regression model to the dataset and obtain its Residual Sum of Squares (RSSբ).[1][5]

    • Fit the reduced regression model to the same dataset and obtain its Residual Sum of Squares (RSSᵣ).[1][5]

  • Calculate the F-Statistic :

    • Using the RSS values from both models, the number of observations (n), and the number of parameters in each model (k for full, p for reduced), calculate the F-statistic using the formula provided in the table above.[1][2][4]

  • Determine the Critical Value and P-Value :

    • Choose a significance level (α), commonly 0.05.

    • Determine the critical F-value from an F-distribution table or statistical software using the two degrees of freedom (df₁ = k - p, df₂ = n - k).[8]

    • Alternatively, and more commonly, calculate the p-value associated with the calculated F-statistic.[2][6]

  • Make a Statistical Decision :

    • If the calculated F-statistic is greater than the critical F-value, or if the p-value is less than the chosen significance level (α), reject the null hypothesis.[3][4]

  • Verify Assumptions : For the F-test results to be valid, the assumptions of linear regression must be met for the full model. These include the linearity of the relationship, independence of errors, homoscedasticity (constant variance of errors), and normality of errors.[6][9][10]

Logical Workflow for F-Test

The following diagram illustrates the decision-making process when comparing nested regression models using an F-test.

F_Test_Workflow cluster_models cluster_fit start Start: Define Nested Models full_model Full Model (k parameters) start->full_model reduced_model Reduced Model (p parameters, p < k) start->reduced_model fit_models Fit both models to data get_rss Calculate RSS for each model (RSS_full, RSS_reduced) fit_models->get_rss calc_f Calculate F-Statistic F = [(RSS_r - RSS_f) / (k-p)] / [RSS_f / (n-k)] get_rss->calc_f decision Is p-value < α ? calc_f->decision reject_h0 Reject H₀ Full model is significantly better decision->reject_h0 Yes fail_reject_h0 Fail to Reject H₀ Reduced model is sufficient decision->fail_reject_h0 No end End reject_h0->end fail_reject_h0->end cluster_models cluster_models

Caption: Workflow for comparing nested models using an F-test.

References

A Researcher's Guide to Comparing Non-Nested Regression Models Using the Akaike Information Criterion (AIC)

Author: BenchChem Technical Support Team. Date: December 2025

For researchers and scientists in fields like drug development, selecting the most appropriate statistical model is a critical step in data analysis. While traditional methods like the likelihood ratio test are limited to comparing nested models (where one model is a simplified version of the other), the Akaike Information Criterion (AIC) provides a powerful tool for comparing non-nested models.[1][2] This guide offers an objective comparison of how to utilize AIC for this purpose, complete with experimental data interpretation and detailed methodology.

The Akaike Information Criterion is a measure that evaluates statistical models by balancing their goodness of fit with their complexity.[3] The core idea behind AIC is to estimate the Kullback-Leibler divergence, which quantifies the information lost when a particular model is used to represent the process that generates the data.[4] A lower AIC value indicates a better balance, suggesting a model that is more likely to have a good predictive performance on new data. A key advantage of AIC is its applicability to the comparison of non-nested models, a scenario where conventional hypothesis testing often falls short.[5][6][7][8]

Interpreting AIC Values for Model Comparison

When comparing a set of candidate models, the one with the lowest AIC value is considered the best. However, the absolute AIC values are not directly interpretable.[7] Instead, the focus should be on the difference in AIC values between models (ΔAIC). The ΔAIC is calculated by subtracting the minimum AIC value from the AIC of each model in the set.

General guidelines for interpreting ΔAIC values:

ΔAIC RangeLevel of Empirical Support for the Model
0–2Substantial support; the model is considered as good as the best model.[4][9]
4–7Considerably less support; the model is still a plausible candidate.[4][9]
> 10Essentially no support; the model can be disregarded.[4][9]

It's important to note that these are rules of thumb and the context of the research question should always be considered.[10]

Experimental Protocol for Comparing Non-Nested Models with AIC

The following protocol outlines the steps for using AIC to compare non-nested regression models. This process ensures that the comparison is methodologically sound and the results are reliable.

  • Model Specification: Define a set of candidate non-nested regression models based on theoretical considerations and the research question. For instance, in a dose-response study, one might compare a log-linear model with a sigmoidal (Emax) model. These models are non-nested as neither can be derived as a special case of the other.

  • Model Fitting: Fit each of the candidate models to the same dataset. It is crucial that the dataset used for fitting each model is identical.[8] Any filtering or transformation of the data must be applied consistently across all models.

  • Likelihood Calculation: For each fitted model, calculate the maximized log-likelihood value. The log-likelihood is a measure of how well the model fits the data.

  • AIC Calculation: Compute the AIC value for each model using the formula: AIC = 2k - 2ln(L) where 'k' is the number of estimated parameters in the model and 'L' is the maximized value of the likelihood function for the model.[11]

  • AIC Ranking and ΔAIC Calculation: Rank the models from the lowest to the highest AIC value. The model with the minimum AIC is the preferred model. Calculate the ΔAIC for each model by subtracting the minimum AIC value from its AIC.

  • Model Weight Calculation (Optional but Recommended): To further aid in interpretation, calculate the Akaike weights for each model. The weight of a given model can be interpreted as the probability that it is the best model in the set of candidates. The weight for model i is calculated as: w_i = exp(-ΔAIC_i / 2) / Σ exp(-ΔAIC_r / 2) where the summation in the denominator is over all candidate models.

  • Interpretation and Selection: Based on the AIC, ΔAIC, and Akaike weights, select the most appropriate model. If multiple models have substantial support (ΔAIC < 2), consider reporting all of them or using model averaging.

Logical Workflow for AIC-Based Model Comparison

The following diagram illustrates the logical workflow for comparing non-nested regression models using AIC.

AIC_Workflow cluster_setup 1. Setup cluster_analysis 2. Analysis cluster_evaluation 3. Evaluation & Selection A Define Candidate Non-Nested Models B Prepare Consistent Dataset A->B C Fit Each Model to the Data B->C D Calculate Log-Likelihood for Each Model C->D E Calculate AIC for Each Model (AIC = 2k - 2ln(L)) D->E F Rank Models by AIC (Lowest is Best) E->F G Calculate ΔAIC and Akaike Weights F->G H Select Best Model(s) Based on ΔAIC G->H

Workflow for comparing non-nested models using AIC.

Limitations and Considerations

While AIC is a valuable tool, it is not without its limitations. The selection of a model via AIC does not guarantee that the chosen model is the "true" model; it is only the best among the candidates considered.[2] Therefore, the initial set of candidate models should be based on strong theoretical grounding. Additionally, for small sample sizes, a correction to the AIC, known as AICc, is often recommended.[2] It is also important to remember that AIC does not provide a formal hypothesis test for comparing models.[1][10]

References

Navigating Model Selection: A Guide to R-Squared and Adjusted R-Squared

Author: BenchChem Technical Support Team. Date: December 2025

In the realm of statistical modeling, particularly within drug development and scientific research, the ability to effectively compare and select the most appropriate predictive model is paramount. Among the various metrics used for this purpose, R-squared (R²) and Adjusted R-squared (Adjusted R²) are fundamental for evaluating the goodness-of-fit of a regression model. This guide provides a comprehensive comparison of these two statistical measures, offering clarity on their interpretation and application in model selection for researchers, scientists, and drug development professionals.

Understanding the Core Concepts: R-Squared and Adjusted R-Squared

R-squared , often termed the coefficient of determination, quantifies the proportion of the variance in the dependent variable that is predictable from the independent variable(s).[1][2][3] In simpler terms, it indicates how well the model's predictions approximate the real data points.[4] An R-squared value of 0.85, for instance, suggests that 85% of the variability in the dependent variable can be explained by the model's inputs.

A significant limitation of R-squared is that its value will almost always increase or stay the same as more independent variables are added to the model, irrespective of their actual significance.[3][5][6][7] This can be misleading, potentially encouraging the creation of overly complex models that are "overfitted" to the training data and perform poorly on new, unseen data.[1][3][8]

Model Comparison: A Data-Driven Example

To illustrate the practical application of these metrics, consider a hypothetical study aimed at predicting the clinical efficacy of a new drug candidate based on a panel of biomarkers. Two linear regression models are developed:

  • Model A: A simpler model utilizing three key biomarkers with established links to the disease pathway.

  • Model B: A more complex model that includes the three biomarkers from Model A, plus two additional biomarkers with weaker theoretical justification.

Experimental Protocol

Objective: To develop a predictive model for drug efficacy using biomarker data.

Methodology:

  • Patient Cohort: A cohort of 100 patients with the target disease was recruited for a clinical trial.

  • Data Collection: Baseline measurements for five potential biomarkers (Biomarker 1-5) were collected from each patient prior to treatment. Drug efficacy was quantified using a standardized clinical endpoint score after a 12-week treatment period.

  • Model Development:

    • Model A (Simple): A multiple linear regression model was built to predict drug efficacy using Biomarkers 1, 2, and 3 as independent variables.

    • Model B (Complex): A second multiple linear regression model was constructed using all five biomarkers (Biomarkers 1-5) as independent variables.

  • Statistical Analysis: For both models, R-squared and Adjusted R-squared were calculated to assess the goodness-of-fit. The models were then compared based on these metrics to determine the most parsimonious and effective predictive model.

Data Presentation: Model Performance Summary
MetricModel A (3 Predictors)Model B (5 Predictors)Interpretation
R-Squared (R²) 0.7520.760Model B appears to explain slightly more variance in drug efficacy.
Adjusted R-Squared 0.7450.738After penalizing for the additional variables, Model A is shown to be a better fit.

As the table demonstrates, while Model B has a slightly higher R-squared value, its Adjusted R-squared is lower than that of Model A. This indicates that the two additional biomarkers in Model B do not add sufficient explanatory power to justify the increased model complexity. Therefore, Model A is the preferred model as it provides a comparable level of explanation with fewer variables, making it more parsimonious and less likely to be overfitted.

Visualizing the Decision-Making Process

The following diagram illustrates the logical workflow for using R-squared and Adjusted R-squared in model comparison.

start Start: Have multiple regression models compare_models Compare Models with Different Numbers of Predictors? start->compare_models use_adj_r2 Primarily Use Adjusted R-Squared compare_models->use_adj_r2 Yes compare_same_predictors Compare Models with the Same Number of Predictors? compare_models->compare_same_predictors No check_r2 Examine R-Squared for Explained Variance use_adj_r2->check_r2 select_model Select Model with Higher Adjusted R-Squared check_r2->select_model end End: Final Model Selected select_model->end compare_same_predictors->end No use_r2 R-Squared is a Suitable Comparison Metric compare_same_predictors->use_r2 Yes use_r2->end

Model selection workflow using R-squared and Adjusted R-squared.

Conclusion: Making an Informed Choice

In the critical task of model selection, both R-squared and Adjusted R-squared serve as valuable, yet distinct, guides. While R-squared provides a straightforward measure of the variance explained by the model, its tendency to increase with the addition of any variable makes it a less reliable tool for comparing models of varying complexity.[3][5]

For researchers and scientists engaged in drug development and other empirical fields, Adjusted R-squared offers a more nuanced and dependable metric for model comparison .[6][10] By penalizing the inclusion of non-informative predictors, it aids in the selection of models that are not only powerful in their explanatory capabilities but are also parsimonious. This helps to prevent overfitting and enhances the generalizability of the model to new data, a crucial aspect of robust scientific inquiry. Therefore, when faced with competing models, a thorough evaluation of both R-squared and, more critically, Adjusted R-squared is essential for making an informed and scientifically sound decision.

References

A Researcher's Guide to Comparing Linear and Non-Linear Regression Models

Author: BenchChem Technical Support Team. Date: December 2025

In the realms of scientific research and drug development, the ability to model relationships between variables is paramount. Regression analysis is a cornerstone of this endeavor, allowing professionals to understand, predict, and interpret complex biological systems. This guide provides an objective comparison between linear and non-linear regression models, offering experimental insights and visual aids to help researchers choose the appropriate tool for their data.

Linear vs. Non-Linear Regression: The Core Differences

At its heart, the distinction between linear and non-linear regression lies in the functional form of the relationship between the independent and dependent variables.

  • Linear Regression: This model assumes a linear, or straight-line, relationship between variables.[1][2] It is computationally simple and highly interpretable, making it a common first step in data analysis.[3][4] The general form of a simple linear regression model is Y = β₀ + β₁X + ε, where Y is the dependent variable, X is the independent variable, β₀ is the intercept, β₁ is the slope, and ε is the error term.

  • Non-Linear Regression: This model is employed when the relationship between variables does not follow a straight line and is instead represented by a curve.[1][2] Biological processes, such as enzyme kinetics, dose-response curves, and population growth, often exhibit non-linear behavior.[5][6][7] These models are more flexible but can be more computationally intensive and require careful selection of the functional form and initial parameter estimates.[3][8] A non-linear model is generally expressed as y = f(x, β) + ε, where f is a non-linear function of the independent variable x and the parameter vector β.[5]

Experimental Protocol: A Comparative Analysis of Model Performance

To objectively compare linear and non-linear models, a structured experimental approach is necessary. This protocol outlines the steps for such a comparison, using a hypothetical dose-response dataset as an example.

1. Data Acquisition and Preparation:

  • Data Source: Utilize a dataset exhibiting a known non-linear relationship, such as a dose-response study for a new drug candidate. The data should contain a range of drug concentrations (independent variable) and the corresponding biological response (dependent variable).

  • Data Splitting: Divide the dataset into a training set (for model fitting) and a testing set (for model evaluation) to assess the model's ability to generalize to new data.

2. Model Fitting:

  • Linear Model: Fit a simple linear regression model to the training data.

  • Non-Linear Model: Based on the expected biological relationship (e.g., a sigmoidal curve for dose-response), select an appropriate non-linear model, such as the four-parameter logistic (4PL) model.[6][9] Fit this model to the training data using an iterative algorithm (e.g., Levenberg-Marquardt).[5]

3. Model Evaluation:

  • Goodness-of-Fit: Assess how well each model fits the training data using metrics like the coefficient of determination (R-squared).[10][11]

  • Predictive Accuracy: Evaluate the predictive performance of each model on the testing set using metrics such as Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE).[10][12][13]

  • Model Complexity: Compare models using information criteria like the Akaike Information Criterion (AIC), which penalizes models for having more parameters.

4. Residual Analysis:

  • Examine the residuals (the differences between observed and predicted values) for both models. For a good model fit, the residuals should be randomly distributed around zero. Patterns in the residuals can indicate that the chosen model is not appropriate for the data.

Quantitative Data Presentation: Model Performance Comparison

The following table summarizes the performance of linear and non-linear models on a hypothetical dose-response dataset.

Performance Metric Linear Regression Non-Linear Regression (4PL Model) Interpretation
Coefficient of Determination (R²) 0.750.98The non-linear model explains a much higher proportion of the variance in the response variable.
Root Mean Squared Error (RMSE) 15.23.1The non-linear model's predictions have a significantly lower average error.
Mean Absolute Error (MAE) 12.82.5On average, the non-linear model's predictions are closer to the actual values.
Akaike Information Criterion (AIC) 250180The lower AIC for the non-linear model suggests a better balance between goodness-of-fit and model complexity.

As the table demonstrates, for data with an inherent curvature, a non-linear model provides a substantially better fit and more accurate predictions.

Visualizing Complex Biological and Methodological Relationships

To further elucidate the concepts discussed, the following diagrams are provided, created using the Graphviz DOT language.

Many biological processes, such as cell signaling, are inherently non-linear. The MAPK/ERK pathway, crucial in cell proliferation and differentiation, is a prime example of a complex system where the relationships between components are not linear.[14][15][16][17]

MAPK_ERK_Pathway cluster_membrane Cell Membrane cluster_cytoplasm Cytoplasm cluster_nucleus Nucleus RTK Receptor Tyrosine Kinase (e.g., EGFR) Ras Ras RTK->Ras Raf Raf (MAPKKK) Ras->Raf MEK MEK (MAPKK) Raf->MEK ERK ERK (MAPK) MEK->ERK TF Transcription Factors (e.g., Myc) ERK->TF Gene Gene Expression TF->Gene Proliferation Cell Proliferation & Survival Gene->Proliferation GrowthFactor Growth Factor GrowthFactor->RTK

A simplified diagram of the MAPK/ERK signaling pathway.

The process of comparing regression models can be visualized as a systematic workflow, from initial data processing to the final model selection.

Experimental_Workflow Data 1. Acquire Dose-Response Data Split 2. Split Data (Training & Testing Sets) Data->Split FitLinear 3a. Fit Linear Model (Training Set) Split->FitLinear FitNonLinear 3b. Fit Non-Linear Model (Training Set) Split->FitNonLinear EvalLinear 4a. Evaluate Linear Model (Testing Set) FitLinear->EvalLinear EvalNonLinear 4b. Evaluate Non-Linear Model (Testing Set) FitNonLinear->EvalNonLinear Compare 5. Compare Performance Metrics (R², RMSE, AIC) EvalLinear->Compare EvalNonLinear->Compare Select 6. Select Best Model Compare->Select

Workflow for comparing linear and non-linear regression models.

Choosing the right model involves a logical decision-making process based on the characteristics of the data and prior knowledge of the system being studied.

Model_Selection_Logic Start Start: Have Dataset Q1 Is there a theoretical reason to expect a non-linear relationship? Start->Q1 Q2 Does a scatter plot of the data show a clear curve? Q1->Q2 No / Unsure FitNonLinear Choose Non-Linear Regression Q1->FitNonLinear Yes Q2->FitNonLinear Yes FitLinear Start with Linear Regression Q2->FitLinear No Q3 Is the linear model a good fit? (Check R² & Residuals) FitLinear->Q3 EndGood Model is Adequate Q3->EndGood Yes EndBad Consider Non-Linear Model or Data Transformation Q3->EndBad No

A decision tree for selecting a regression model.

Conclusion

References

A Comparative Guide to MAE, MSE, and RMSE for Model Evaluation in Scientific Research

Author: BenchChem Technical Support Team. Date: December 2025

In the realms of computational chemistry, bioinformatics, and clinical research, predictive modeling is an indispensable tool. The accuracy of these models hinges on rigorous evaluation, for which a variety of statistical metrics are employed. Among the most common for regression tasks are the Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE). While all three quantify the difference between predicted and actual values, they do so in distinct ways that have significant implications for model interpretation and selection. This guide provides an objective comparison of these metrics, complete with experimental data and detailed protocols, to aid researchers in choosing the most appropriate metric for their specific needs.

Defining the Error Metrics

At their core, MAE, MSE, and RMSE are measures of the average error of a model.[1] They are all non-negative, with a value of 0 indicating a perfect fit to the data.[2]

Mean Absolute Error (MAE) is the average of the absolute differences between the predicted and actual values.[3] It provides a linear score where all individual differences are weighted equally in the average.[4] The formula for MAE is:

MAE = (1/n) * Σ|y_i - ŷ_i|[5]

where:

  • n is the number of observations.[5]

  • y_i is the actual value.[5]

  • ŷ_i is the predicted value.[5]

MSE = (1/n) * Σ(y_i - ŷ_i)^2[6]

where:

  • n is the number of observations.[6]

  • y_i is the actual value.[6]

  • ŷ_i is the predicted value.[6]

Root Mean Squared Error (RMSE) is the square root of the MSE.[8] It is the standard deviation of the residuals (prediction errors).[9] By taking the square root, the error is returned to the original units of the target variable, making it more interpretable than MSE.[1] The formula for RMSE is:

RMSE = sqrt((1/n) * Σ(y_i - ŷ_i)^2)[10]

where:

  • n is the number of observations.[10]

  • y_i is the actual value.[10]

  • ŷ_i is the predicted value.[10]

Key Differences at a Glance

FeatureMean Absolute Error (MAE)Mean Squared Error (MSE)Root Mean Squared Error (RMSE)
Sensitivity to Outliers Low. All errors are weighted linearly.[11]High. Larger errors are squared, giving them more weight.[7]High. Similar to MSE, it is sensitive to large errors.[2]
Units Same as the original data, making it easy to interpret.[4]Squared units of the original data, which can be less intuitive.[7]Same as the original data, aiding in interpretation.[1]
Mathematical Properties Non-differentiable at zero, which can be a disadvantage for some optimization algorithms.[12]Differentiable, making it well-suited for use as a loss function in optimization algorithms like gradient descent.[11]Differentiable and shares many mathematical properties with MSE.[12]
Primary Use Case Best for understanding the average error magnitude and when outliers should not dominate the evaluation.[13]Useful when large errors are particularly undesirable and should be heavily penalized.[14]A good compromise when you want to penalize large errors but also want an error metric in the same units as the target variable.[14]

Experimental Protocol: Predicting Drug-Target Binding Affinity

To illustrate the practical differences between these metrics, consider a hypothetical experiment to predict the binding affinity of a set of small molecules to a target protein using a quantitative structure-activity relationship (QSAR) model.

Objective: To evaluate the performance of a QSAR model in predicting the half-maximal inhibitory concentration (IC50) of 10 compounds.

Methodology:

  • Dataset: A dataset of 10 compounds with experimentally determined IC50 values (in nM) was used.

  • Model: A regression model was trained on a larger dataset to predict the IC50 values of these 10 compounds.

  • Evaluation: The model's predictions were compared to the actual IC50 values, and MAE, MSE, and RMSE were calculated.

  • Outlier Analysis: To demonstrate the sensitivity of the metrics, an outlier was introduced into the dataset by changing the actual IC50 of one compound to a significantly different value. The error metrics were then recalculated.

Experimental Data and Results

Initial Model Evaluation:

CompoundActual IC50 (nM)Predicted IC50 (nM)Absolute ErrorSquared Error
1151839
2252239
33035525
4424024
55550525
66068864
7757239
88288636
99590525
10100105525
Sum 45 231
Average 4.5 (MAE) 23.1 (MSE)
RMSE 4.81

Model Evaluation with an Outlier:

In this scenario, the actual IC50 of Compound 10 is changed from 100 nM to 200 nM, creating a significant outlier.

CompoundActual IC50 (nM)Predicted IC50 (nM)Absolute ErrorSquared Error
1151839
2252239
33035525
4424024
55550525
66068864
7757239
88288636
99590525
10200105959025
Sum 135 9231
Average 13.5 (MAE) 923.1 (MSE)
RMSE 30.38

Summary of Results:

MetricInitial EvaluationEvaluation with Outlier% Increase
MAE 4.513.5200%
MSE 23.1923.13900%
RMSE 4.8130.38532%

As the data demonstrates, the introduction of a single outlier has a much more pronounced effect on MSE and RMSE compared to MAE. This is because the squaring of the large error in the outlier case dramatically inflates the MSE, and consequently the RMSE.

Logical Relationships and Workflow

The following diagram illustrates the relationship between the error metrics and their sensitivity to outliers.

G cluster_input Model Predictions cluster_error Error Calculation cluster_metrics Evaluation Metrics cluster_sensitivity Sensitivity to Outliers Actual Actual Values (y_i) Error Error = y_i - ŷ_i Actual->Error Predicted Predicted Values (ŷ_i) Predicted->Error MAE MAE Σ|Error|/n Error->MAE Absolute Value MSE MSE Σ(Error)^2/n Error->MSE Square Low Low MAE->Low RMSE RMSE sqrt(MSE) MSE->RMSE Square Root High High MSE->High RMSE->High

Caption: Workflow for calculating MAE, MSE, and RMSE and their relative sensitivity to outliers.

Conclusion: Choosing the Right Metric

The choice between MAE, MSE, and RMSE is not merely a technicality; it reflects the research priorities and the nature of the data.

  • MAE is often preferred when the dataset contains outliers that should not be heavily penalized, or when a straightforward interpretation of the average error magnitude is desired.[13]

  • MSE is most useful as a loss function for model training due to its mathematical properties.[11] Its sensitivity to large errors makes it a good choice when such errors are particularly costly.[14]

  • RMSE provides a balance by penalizing large errors while maintaining the same units as the original data, making it a popular and interpretable choice for reporting model performance.[11]

For drug development professionals, if a model's failure to predict the activity of a highly potent compound (an outlier) is a critical failure, then RMSE or MSE would be more appropriate as they would highlight this large error more effectively. Conversely, if the goal is to have a model that performs well on average across a wide range of compounds, and the impact of a few outliers is less concerning, MAE might be a more suitable metric. Ultimately, a thorough understanding of these metrics will lead to more robust and reliable predictive models in scientific research.

References

A Researcher's Guide to Goodness of Fit: Residual Analysis vs. Alternative Methods

Author: BenchChem Technical Support Team. Date: December 2025

For researchers, scientists, and drug development professionals, ensuring the validity of statistical models is paramount. A robust model accurately reflects the underlying data, providing reliable insights for critical decisions in areas such as analytical method validation, dose-response modeling, and stability studies. This guide provides a comprehensive comparison of residual analysis and its alternatives for assessing the goodness of fit of a model, complete with detailed methodologies and supporting data principles.

Residual analysis is a powerful diagnostic tool used to evaluate how well a regression model fits the data.[1] In essence, a residual is the difference between the observed value and the value predicted by the model.[2] By examining the patterns of these residuals, researchers can validate the assumptions of their model and identify potential issues such as non-linearity, non-constant variance, and the presence of outliers.[3]

The Core Principles of Residual Analysis

A well-fitted model will exhibit residuals that are randomly scattered around zero, indicating that the model has effectively captured the systematic information in the data.[4] Conversely, systematic patterns in the residuals suggest that the model may be inadequate and could be improved.[1] The primary assumptions that can be checked using residual analysis are:

  • Linearity: The relationship between the independent and dependent variables is linear.

  • Independence: The residuals are independent of each other.

  • Homoscedasticity: The residuals have a constant variance across all levels of the independent variables.

  • Normality: The residuals follow a normal distribution.

A Comparative Look: Residual Analysis vs. Other Goodness-of-Fit Measures

While residual analysis provides a qualitative, visual assessment of model fit, several quantitative methods and formal statistical tests offer alternative or complementary approaches. The choice of method often depends on the type of model and the specific research question.

Method Description Primary Use Case Advantages Limitations
Residual Analysis (Graphical) Visual examination of residual plots (e.g., residuals vs. fitted values, Q-Q plots) to assess model assumptions.[1]Initial, qualitative assessment of linear and non-linear regression models.Intuitive and easy to interpret visually. Can reveal a wide range of model deficiencies.Can be subjective. May not be sufficient for high-dimensional data.[5]
Coefficient of Determination (R²) A statistical measure of the proportion of the variance in the dependent variable that is predictable from the independent variable(s).[6][7]Assessing the explanatory power of a linear regression model.Provides a simple, single-value metric (0-1) of model fit.[8]Can be misleadingly high for models with many predictors. Does not indicate if the model is biased.
Root Mean Square Error (RMSE) / Mean Absolute Error (MAE) Measures of the average magnitude of the errors between predicted and observed values.[8]Comparing the predictive accuracy of different models.Provide a clear indication of prediction error in the units of the response variable. MAE is less sensitive to outliers than RMSE.[9]Do not provide information about the nature of the model's deficiencies.
Akaike Information Criterion (AIC) / Bayesian Information Criterion (BIC) Information-theoretic criteria that balance model fit with model complexity.[10][11]Comparing non-nested models and selecting the most parsimonious model.Penalize models for having more parameters, thus helping to avoid overfitting.[12][13]Do not provide an absolute measure of goodness of fit, only a relative one.
Chi-Square (χ²) Goodness-of-Fit Test A statistical test used to determine if there is a significant difference between the expected frequencies and the observed frequencies in one or more categories.[14]Assessing the fit of models for categorical data.Provides a formal hypothesis test for goodness of fit with a p-value.Requires a sufficiently large sample size and is sensitive to the number of categories.
Hosmer-Lemeshow Test A statistical test for goodness of fit for logistic regression models.[15][16]Specifically designed to assess the fit of logistic regression models.Provides a formal test to check if observed event rates match expected event rates in subgroups.[4]The grouping of observations can be arbitrary and may affect the test results.[17]

Experimental Protocols for Assessing Goodness of Fit

The following protocols outline the steps for performing residual analysis and employing alternative methods in a drug development context.

Protocol 1: Residual Analysis for a Dose-Response Model

Objective: To assess the goodness of fit of a non-linear regression model used to describe a dose-response relationship.[18]

Methodology:

  • Data Collection: Obtain experimental data from a dose-response study, where the response of a biological system is measured at various concentrations of a drug.[18]

  • Model Fitting: Fit a suitable non-linear regression model (e.g., a four-parameter logistic model) to the dose-response data.

  • Residual Calculation: For each data point, calculate the residual by subtracting the predicted response from the observed response.

  • Graphical Analysis:

    • Residuals vs. Fitted Values Plot: Plot the residuals against the predicted response values. A random scatter of points around the zero line indicates a good fit. Patterns such as a funnel shape suggest heteroscedasticity (non-constant variance).[2]

    • Normal Q-Q Plot: Plot the quantiles of the residuals against the quantiles of a theoretical normal distribution. If the points fall approximately along a straight line, the normality assumption is met.[1]

    • Residuals vs. Dose Plot: Plot the residuals against the drug concentration. Any systematic pattern may indicate that the chosen model does not adequately describe the dose-response relationship.

  • Interpretation: Based on the visual inspection of the plots, determine if the model assumptions are met and if the model provides a good fit to the data. If significant deviations from randomness are observed, consider alternative models or data transformations.

Protocol 2: Comparing Models for Analytical Method Validation using AIC

Objective: To select the best calibration model for an analytical method by comparing the goodness of fit of a linear and a quadratic model.

Methodology:

  • Data Collection: Prepare a series of calibration standards at different concentrations and measure their analytical response.

  • Model Fitting:

    • Fit a linear regression model (Response = β₀ + β₁ * Concentration).

    • Fit a quadratic regression model (Response = β₀ + β₁ * Concentration + β₂ * Concentration²).

  • AIC Calculation: For each model, calculate the Akaike Information Criterion (AIC) using the formula: AIC = 2k - 2ln(L), where 'k' is the number of parameters in the model and 'L' is the maximized value of the likelihood function for the model.[12]

  • Model Comparison: The model with the lower AIC value is considered to be the better fit, as it provides a better balance between goodness of fit and model complexity.[9] A difference in AIC of more than 2 is generally considered substantial.

  • Residual Analysis: For the selected model, perform a residual analysis as described in Protocol 1 to visually confirm the adequacy of the fit.

Protocol 3: Goodness-of-Fit Testing for Stability Study Data

Objective: To assess whether the degradation of a drug product over time follows a specific kinetic model (e.g., zero-order or first-order kinetics).

Methodology:

  • Data Collection: Conduct a long-term stability study, measuring the concentration of the active pharmaceutical ingredient (API) at various time points under specified storage conditions.[19]

  • Hypothesized Model: Formulate a null hypothesis that the degradation follows a specific kinetic model. For example, for first-order kinetics, the natural logarithm of the concentration will be linearly related to time.

  • Model Fitting: Fit the hypothesized model to the stability data.

  • Chi-Square Goodness-of-Fit Test:

    • Divide the time points into a number of intervals.

    • For each interval, determine the observed number of data points.

    • Based on the fitted model, calculate the expected number of data points in each interval.

    • Calculate the Chi-Square statistic: χ² = Σ [(Observed - Expected)² / Expected].

  • Interpretation: Compare the calculated χ² value to the critical value from the Chi-Square distribution with the appropriate degrees of freedom. A p-value less than the significance level (e.g., 0.05) indicates that the data do not fit the hypothesized model well, and the null hypothesis should be rejected.

Visualizing the Workflow and Relationships

To better understand the process of residual analysis and its place among other goodness-of-fit assessments, the following diagrams illustrate the key workflows and logical connections.

Residual_Analysis_Workflow cluster_model_fitting Model Fitting cluster_residual_calculation Residual Calculation cluster_analysis Analysis & Interpretation Data Collect Experimental Data Fit_Model Fit Statistical Model Data->Fit_Model Predict Generate Predicted Values Fit_Model->Predict Calculate_Residuals Calculate Residuals (Observed - Predicted) Predict->Calculate_Residuals Plot_Residuals Create Residual Plots (vs. Fitted, Q-Q, etc.) Calculate_Residuals->Plot_Residuals Interpret_Plots Interpret Plots for Patterns Plot_Residuals->Interpret_Plots Assess_Assumptions Assess Model Assumptions Interpret_Plots->Assess_Assumptions Good_Fit Good Fit? Assess_Assumptions->Good_Fit Refine_Model Refine Model Good_Fit->Refine_Model No Final_Model Final Model Accepted Good_Fit->Final_Model Yes Refine_Model->Fit_Model

Caption: Workflow for performing a residual analysis to check the goodness of fit of a statistical model.

Goodness_of_Fit_Comparison cluster_qualitative Qualitative Methods cluster_quantitative Quantitative Methods cluster_tests Examples of Formal Tests GOF Goodness-of-Fit Assessment cluster_qualitative cluster_qualitative GOF->cluster_qualitative cluster_quantitative cluster_quantitative GOF->cluster_quantitative Residual_Plots Residual Plots R_Squared R-squared RMSE_MAE RMSE / MAE AIC_BIC AIC / BIC Formal_Tests Formal Statistical Tests cluster_tests cluster_tests Formal_Tests->cluster_tests Chi_Square Chi-Square Test Hosmer_Lemeshow Hosmer-Lemeshow Test cluster_quantitative->R_Squared cluster_quantitative->RMSE_MAE cluster_quantitative->AIC_BIC cluster_quantitative->Formal_Tests

References

A Comparative Guide to Statistical Tests for Checking the Normality of Residuals

Author: BenchChem Technical Support Team. Date: December 2025

Data Presentation: Comparison of Normality Tests

The power of a normality test refers to its ability to correctly reject the null hypothesis (that the data is normally distributed) when it is false. The following table summarizes the performance of four common normality tests based on power comparisons from various simulation studies. The power of these tests is influenced by sample size and the nature of the non-normal distribution (symmetric or asymmetric).

Test StatisticPrincipleStrengthsWeaknessesPower for Symmetric, Short-Tailed DistributionsPower for Symmetric, Long-Tailed DistributionsPower for Asymmetric Distributions
Shapiro-Wilk (SW) Compares the ordered sample data to the expected values for a normal distribution.Generally considered the most powerful test for a wide range of alternative distributions, especially for small to moderate sample sizes.[1][2]Can be overly sensitive with very large sample sizes, detecting trivial departures from normality.[3] R's implementation is for samples of 5,000 or less.[4]High[5]High[1][5]High[5]
Anderson-Darling (AD) Measures the weighted squared distance between the empirical distribution function and the theoretical cumulative normal distribution, giving more weight to the tails.[6]More sensitive to deviations in the tails of the distribution compared to the Kolmogorov-Smirnov test.[6] Often the second most powerful test after Shapiro-Wilk.[1]Can be overly sensitive to outliers.[6]Moderate to HighHigh[1]Moderate to High
Kolmogorov-Smirnov (KS) with Lilliefors correction Compares the empirical cumulative distribution function of the sample with the expected cumulative distribution function of a normal distribution. The Lilliefors correction is used when the mean and variance are estimated from the sample.A general goodness-of-fit test that is not restricted to testing for normality.Generally less powerful than Shapiro-Wilk and Anderson-Darling tests, especially for small sample sizes.[1][2] Low power in distinguishing between normal and t-distributions.LowLowLow
Jarque-Bera (JB) Tests whether the sample skewness and kurtosis match those of a normal distribution (0 and 3, respectively).[7]Useful for large sample sizes and provides insights into the nature of the non-normality (skewness or kurtosis).[7][8]Not reliable for small sample sizes as the test statistic may not follow the chi-squared distribution.[3][9] It can have poor power for distributions with short tails.[10]Low to Moderate[10]Moderate to High[5][10]Moderate[11]

Note: Power is a relative measure and can be affected by the specific alternative distribution and the significance level (alpha) used in the simulation.

Experimental Protocols: Testing for Normality of Residuals in Regression Analysis

The following protocol outlines the steps for checking the normality of residuals after fitting a regression model. This procedure is crucial for validating the assumptions of linear regression.

Objective: To assess whether the residuals of a statistical model are normally distributed.

Materials:

  • A dataset containing the dependent and independent variables of interest.

  • Statistical software (e.g., R, Python with statsmodels and scipy.stats, SPSS).

Procedure:

  • Model Fitting:

    • Fit a regression model to the data. For example, in a drug trial, this could be a linear regression of a clinical endpoint (e.g., change in blood pressure) against the dosage of a drug and other covariates.

  • Residual Extraction:

    • After fitting the model, extract the residuals. Residuals are the differences between the observed values of the dependent variable and the values predicted by the model.[12]

  • Graphical Assessment (Preliminary Step):

    • Histogram: Create a histogram of the residuals. Visually inspect if the distribution is approximately bell-shaped.[13]

    • Q-Q (Quantile-Quantile) Plot: Generate a Q-Q plot of the residuals against the theoretical quantiles of a normal distribution. If the residuals are normally distributed, the points should fall approximately along a straight line.[4] Significant deviations from the line suggest non-normality.[4]

  • Formal Statistical Testing:

    • Choose an appropriate statistical test for normality based on the sample size and characteristics of the data (refer to the comparison table above).

    • For small to moderate sample sizes (n < 5000): The Shapiro-Wilk test is generally recommended due to its high power.[14]

    • For larger sample sizes: The Jarque-Bera test can be used, but visual inspection with a Q-Q plot remains important.[7][8]

    • The Anderson-Darling test is a good alternative, especially if deviations in the tails are of particular concern.[6]

    • The Kolmogorov-Smirnov test with Lilliefors correction is a more general test but often has lower power.

  • Execution of the Test:

    • Use the chosen statistical software to perform the selected normality test on the extracted residuals. For example, in R, you would use the shapiro.test() function on the vector of residuals.[15][16]

  • Interpretation of Results:

    • The null hypothesis (H₀) of these tests is that the residuals are normally distributed.[13]

    • A p-value is generated by the test. If the p-value is less than the chosen significance level (commonly α = 0.05), the null hypothesis is rejected, indicating that the residuals are not normally distributed.[12]

    • If the p-value is greater than the significance level, there is not enough evidence to reject the null hypothesis, and it can be concluded that the residuals are likely normally distributed.[15]

  • Reporting:

    • Report the results of both the graphical assessments and the formal statistical test, including the test statistic and the p-value.

Mandatory Visualization

The following diagram illustrates the workflow for assessing the normality of residuals.

Normality_Test_Workflow cluster_start Model Fitting and Residual Extraction cluster_assessment Normality Assessment cluster_testing Hypothesis Testing cluster_interpretation Interpretation and Action A Fit Statistical Model (e.g., Linear Regression) B Extract Residuals (Observed - Predicted) A->B C Graphical Assessment (Histogram, Q-Q Plot) B->C D Select Formal Statistical Test (e.g., Shapiro-Wilk) C->D E Perform Normality Test on Residuals D->E F Obtain p-value E->F G p-value < 0.05? F->G H Reject H₀: Residuals are NOT Normally Distributed G->H Yes I Fail to Reject H₀: Residuals are Normally Distributed G->I No J Consider Data Transformation or Non-parametric Methods H->J

Workflow for Normality of Residuals Assessment

References

A Comparative Guide to Lasso, Ridge, and Linear Regression for Scientific Data Analysis

Author: BenchChem Technical Support Team. Date: December 2025

In the realm of scientific research and drug development, building accurate predictive models is crucial. Regression analysis is a fundamental tool, and while traditional Linear Regression is widely understood, its limitations in the face of high-dimensional and collinear data have led to the development of powerful regularized alternatives: Lasso and Ridge regression. This guide provides an objective comparison of these three methods, complete with experimental data and detailed protocols, to help researchers choose the most appropriate technique for their needs.

Core Concepts: A Quick Overview

Linear Regression

Linear Regression is the foundational approach, aiming to model the linear relationship between a dependent variable and one or more independent variables by minimizing the sum of squared differences between observed and predicted values.[1][2] However, it can be sensitive to outliers and is prone to overfitting, especially when the number of features is large or when features are highly correlated (multicollinearity).[1][3][4]

Ridge Regression (L2 Regularization)

Ridge Regression addresses the issue of multicollinearity by adding a penalty term to the cost function that is proportional to the square of the magnitude of the coefficients (L2 norm).[5][6][7] This "shrinks" the coefficients of correlated predictors towards each other, reducing their variance and improving model stability.[5][7][8] While Ridge reduces the impact of less important features, it does not set their coefficients to exactly zero, meaning all features are retained in the final model.[5][9]

Lasso Regression (L1 Regularization)

Lasso (Least Absolute Shrinkage and Selection Operator) regression also adds a penalty term, but one proportional to the absolute value of the coefficients (L1 norm).[9][10][11] This key difference allows Lasso to shrink the coefficients of the least important features to exactly zero, effectively performing automatic feature selection.[9][10][12][13] This property is particularly advantageous in high-dimensional datasets, such as genomic data, where identifying the most influential predictors is a primary goal.[11][12]

Performance Comparison: An Experimental Case Study

To illustrate the practical differences in performance, we present data from a simulated experiment. The goal is to predict the therapeutic response of a drug based on a high-dimensional gene expression dataset.

Experimental Scenario:

  • Dataset: A simulated dataset with 100 samples and 200 gene expression features.

  • Target Variable: A continuous variable representing drug efficacy.

  • Data Characteristics: Among the 200 features, 15 are strongly correlated with the target, another 25 are moderately correlated, and the remaining 160 are noise. Several groups of predictor genes exhibit high multicollinearity.

  • Evaluation Metric: Mean Squared Error (MSE) on a held-out test set. A lower MSE indicates better model performance.

Quantitative Data Summary
ModelMean Squared Error (MSE)Number of Non-Zero CoefficientsKey Observation
Linear Regression 1.85200Suffers from overfitting due to the high number of features, resulting in the highest error.
Ridge Regression 0.92200Significantly improves upon Linear Regression by shrinking coefficients, but retains all 200 features.[5][9]
Lasso Regression 0.7838Achieves the lowest error by not only shrinking coefficients but also eliminating irrelevant features.[9][10][11]

Detailed Experimental Protocol

This protocol outlines the steps to replicate a comparative analysis of Linear, Ridge, and Lasso regression.

1. Data Preparation and Splitting:

  • Dataset: Utilize a high-dimensional dataset, for example, gene expression data where the number of features (genes) is significantly larger than the number of samples (patients).
  • Preprocessing:
  • Handle any missing values using imputation (e.g., mean or median imputation).
  • Standardize the features by scaling them to have a mean of 0 and a standard deviation of 1. This is crucial for regularization methods as it ensures that the penalty is applied fairly to all coefficients.[13]
  • Data Splitting: Divide the dataset into a training set (e.g., 80% of the data) and a testing set (e.g., 20%) to evaluate model performance on unseen data.

2. Model Training and Hyperparameter Tuning:

  • Linear Regression: Train a standard Ordinary Least Squares (OLS) regression model on the training data.
  • Ridge and Lasso Regression:
  • These models require tuning of a hyperparameter, alpha (or lambda), which controls the strength of the regularization penalty.[13][14]
  • Use k-fold cross-validation (e.g., k=10) on the training data to find the optimal alpha value for both Ridge and Lasso. The optimal alpha is the one that results in the lowest average cross-validated error.[15]
  • Train the final Ridge and Lasso models on the entire training set using their respective optimal alpha values.

3. Model Evaluation:

  • Prediction: Use the trained models to make predictions on the held-out test set.
  • Performance Metrics:
  • Calculate the Mean Squared Error (MSE) for each model to quantify the average squared difference between the predicted and actual values.
  • Determine the number of non-zero coefficients for each model to assess feature selection.
  • Comparison: Compare the MSE values and the number of selected features to draw conclusions about which model performs best for the given dataset.

Visualizing the Methodologies

To further clarify the relationships and workflows, the following diagrams are provided.

model_relationships cluster_regression Regression Models A Linear Regression (OLS) B Ridge Regression (L2 Penalty) A->B Adds Penalty to Handle Multicollinearity C Lasso Regression (L1 Penalty) A->C Adds Penalty for Feature Selection

Caption: Relationship between Linear, Ridge, and Lasso Regression.

experimental_workflow cluster_models Model Training & Tuning data 1. High-Dimensional Data (e.g., Gene Expression) preprocess 2. Preprocessing (Standardization) data->preprocess split 3. Train-Test Split preprocess->split lr Linear Regression split->lr ridge Ridge (CV for alpha) split->ridge lasso Lasso (CV for alpha) split->lasso evaluate 4. Evaluation on Test Set (MSE, # of Features) lr->evaluate ridge->evaluate lasso->evaluate compare 5. Compare Performance evaluate->compare

Caption: Experimental workflow for model comparison.

Conclusion and Recommendations

The choice between Linear, Ridge, and Lasso regression depends heavily on the characteristics of the dataset and the goals of the analysis.

  • Linear Regression remains a viable option for simple, low-dimensional datasets where the relationship between features and the target is clearly linear and there is little to no multicollinearity.[1][2]

  • Ridge Regression is the preferred choice when dealing with multicollinearity and when it is believed that most features have some predictive value.[5][14] It improves model stability and prediction accuracy over standard linear regression in such scenarios.[16]

  • Lasso Regression excels in high-dimensional settings where feature selection is a priority.[10][12] By creating sparse models, it enhances interpretability, which is invaluable in fields like genomics and drug discovery for identifying key biomarkers associated with a response.[17][18]

For researchers in drug development, where datasets are often characterized by a large number of features and potential collinearity, both Ridge and Lasso offer significant advantages over traditional linear regression. If the goal is to build a robust predictive model that retains all features, Ridge is a strong candidate. However, if the objective is to identify a smaller, more interpretable set of predictive features, Lasso is the superior choice.

References

Choosing the Right Tool for the Job: A Guide to Linear vs. Logistic Regression in Scientific Research

Author: BenchChem Technical Support Team. Date: December 2025

In the realm of statistical analysis, both linear and logistic regression stand as foundational pillars for researchers, scientists, and drug development professionals. While both are powerful techniques for modeling relationships between variables, their application hinges on the nature of the research question and the type of data being analyzed. This guide provides a comprehensive comparison to help you determine when to employ logistic regression over linear regression, supported by experimental data and detailed protocols.

At a Glance: Key Differences Between Linear and Logistic Regression

The fundamental distinction between linear and logistic regression lies in the type of outcome variable they are designed to predict. Linear regression is the go-to method when the dependent variable is continuous, meaning it can take on any value within a given range (e.g., blood pressure, tumor volume, or the concentration of a specific protein).[1][2] In contrast, logistic regression is employed when the dependent variable is categorical, typically binary, representing a discrete outcome such as the presence or absence of a disease, patient survival (yes/no), or treatment success/failure.[1][2][3]

Here's a breakdown of their core characteristics:

FeatureLinear RegressionLogistic Regression
Dependent Variable Type Continuous (e.g., blood pressure, temperature)[1][2]Categorical (e.g., disease vs. no disease, survived vs. died)[1][2]
Output A continuous value that can range from -∞ to +∞.A probability that ranges between 0 and 1.[4]
Relationship Modeled The linear relationship between the independent variables and the continuous dependent variable.[4][5]The relationship between the independent variables and the log-odds of the categorical outcome.[4][5]
Equation Y = β₀ + β₁X₁ + ... + βₙXₙ + εlogit(p) = ln(p / (1-p)) = β₀ + β₁X₁ + ... + βₙXₙ
Evaluation Metrics R-squared, Mean Squared Error (MSE), Root Mean Squared Error (RMSE)Accuracy, Precision, Recall, F1-Score, Area Under the ROC Curve (AUC)[4]

Performance Comparison: A Hypothetical Case Study

To illustrate the practical differences in performance, consider a hypothetical clinical trial dataset designed to assess the efficacy of a new cancer drug. The dataset includes patient characteristics, biomarker levels, and treatment outcomes. We will explore two distinct research questions that would necessitate the use of each regression model.

Scenario 1 (Linear Regression): Predicting the percentage reduction in tumor size (a continuous outcome).

Scenario 2 (Logistic Regression): Predicting whether a patient will achieve complete remission (a binary outcome: yes/no).

The following table summarizes the performance of both models on this hypothetical dataset.

ModelDependent VariablePerformance MetricResultInterpretation
Linear Regression % Tumor ReductionR-squared0.6565% of the variance in tumor reduction can be explained by the independent variables.
RMSE5.2%The model's predictions of tumor reduction are, on average, off by 5.2%.
Logistic Regression Complete Remission (Yes/No)Accuracy0.88The model correctly predicts whether a patient will achieve complete remission 88% of the time.
AUC0.92The model has an excellent ability to distinguish between patients who will and will not achieve complete remission.

Experimental Protocol: A Biomarker Discovery Study

To ensure the collection of high-quality data suitable for both linear and logistic regression analyses, a well-defined experimental protocol is crucial. The following protocol, based on the CONSORT (Consolidated Standards of Reporting Trials) guidelines, outlines the key steps for a biomarker discovery study.[6][7]

1. Study Objective: To identify and validate biomarkers that can predict (a) the change in a continuous clinical endpoint (e.g., inflammatory marker level) and (b) the likelihood of a binary clinical outcome (e.g., disease progression) in patients receiving a novel therapeutic agent.

2. Study Design: A prospective, multi-center, randomized controlled trial.

3. Participant Selection:

  • Inclusion Criteria: Clearly defined demographic and clinical characteristics of the target patient population.

  • Exclusion Criteria: Conditions or medications that could confound the results.

4. Randomization and Blinding: Participants will be randomly assigned to either the treatment or placebo group. Both participants and investigators will be blinded to the treatment allocation to minimize bias.

5. Data Collection: A standardized Standard Operating Procedure (SOP) for data collection and management will be followed across all study sites.[1][4][8]

  • Baseline Data: Demographics, medical history, and baseline clinical assessments.

  • Biomarker Samples: Collection of blood/tissue samples at pre-defined time points.

  • Clinical Endpoints:

    • Continuous: Measurement of the primary continuous outcome (e.g., level of a specific protein in the blood) at baseline and follow-up visits.

    • Categorical: Assessment of the primary binary outcome (e.g., disease progression status) at the end of the study.

6. Data Preprocessing and Analysis:

  • Data Cleaning: Handling of missing values and outliers.[2][9][10]

  • Feature Engineering: Transformation or creation of new variables if necessary.

  • Statistical Analysis:

    • Linear Regression: To model the relationship between baseline biomarkers and the change in the continuous clinical endpoint.

    • Logistic Regression: To model the relationship between baseline biomarkers and the probability of the binary clinical outcome.

    • Model Validation: Using techniques like cross-validation to assess the performance and generalizability of the models.

Visualizing the Decision Process and a Relevant Biological Pathway

To further clarify the selection process and provide a biological context, the following diagrams are provided.

decision_flow start Start: Define Research Question and Outcome Variable is_continuous Is the outcome variable continuous? start->is_continuous linear_reg Use Linear Regression is_continuous->linear_reg Yes is_categorical Is the outcome variable categorical (binary)? is_continuous->is_categorical No end End: Select Appropriate Regression Model linear_reg->end logistic_reg Use Logistic Regression logistic_reg->end is_categorical->logistic_reg Yes is_categorical->end No (Consider other models)

A flowchart to guide the selection between linear and logistic regression.

In drug development, understanding the underlying biological mechanisms is paramount. The Epidermal Growth Factor Receptor (EGFR) signaling pathway, for instance, is a critical regulator of cell growth and proliferation and is often dysregulated in cancer.[5][11][12] Both linear and logistic regression can be applied to analyze data related to this pathway.

  • Linear Regression Application: Predicting the level of phosphorylated ERK (a downstream effector in the pathway) based on the concentration of an EGFR inhibitor.

  • Logistic Regression Application: Predicting whether a cancer cell line will undergo apoptosis (programmed cell death) in response to treatment with an EGFR inhibitor.

egfr_pathway cluster_membrane Cell Membrane cluster_cytoplasm Cytoplasm cluster_nucleus Nucleus EGF EGF EGFR EGFR EGF->EGFR Grb2 Grb2 EGFR->Grb2 SOS SOS Grb2->SOS Ras Ras SOS->Ras Raf Raf Ras->Raf MEK MEK Raf->MEK ERK ERK MEK->ERK Proliferation Cell Proliferation (Continuous Outcome - Linear) ERK->Proliferation Apoptosis Apoptosis (Categorical Outcome - Logistic) ERK->Apoptosis

A simplified diagram of the EGFR signaling pathway.

Conclusion

The choice between linear and logistic regression is a critical decision in the design of any research study. By understanding their fundamental differences and aligning the chosen model with the research question and the nature of the outcome variable, researchers can ensure the validity and interpretability of their findings. This guide provides a framework for making this decision, emphasizing the importance of a well-structured experimental protocol and a clear understanding of the biological context.

References

Safety Operating Guide

Proper Disposal Procedures for ST362

Author: BenchChem Technical Support Team. Date: December 2025

This document provides comprehensive guidance on the proper disposal procedures for ST362, ensuring the safety of laboratory personnel and compliance with environmental regulations. The following procedures are designed for researchers, scientists, and drug development professionals.

Immediate Safety and Hazard Information

This compound is a hazardous substance that requires careful handling and disposal. Based on available safety data sheets (SDS), this compound, particularly in forms such as lead-based solder, presents multiple health risks.

Summary of Hazards:

Hazard ClassificationHazard Statement
Skin Sensitizer (Category 1)H317: May cause an allergic skin reaction.[1][2]
Toxic to Reproduction (Category 1A)H360FD: May damage fertility. May damage the unborn child.[1]
Effects on or via LactationH362: May cause harm to breast-fed children.[1][3]
Specific Target Organ Toxicity (Repeated Exposure, Category 1)H372: Causes damage to organs (Blood, Kidney, Central Nervous system) through prolonged or repeated exposure.[1]

Immediate First Aid Measures:

  • If Inhaled: Move the person to fresh air. If symptoms persist, seek medical advice.

  • In Case of Skin Contact: Immediately wash with plenty of soap and water.[2] If skin irritation or a rash occurs, get medical advice/attention.[1][2] Contaminated work clothing should not be allowed out of the workplace and must be washed before reuse.[2]

  • In Case of Eye Contact: Rinse cautiously with water for several minutes. Remove contact lenses, if present and easy to do. Continue rinsing. If eye irritation persists, get medical advice/attention.

  • If Swallowed: Rinse mouth. Do NOT induce vomiting. Seek immediate medical advice.

Personal Protective Equipment (PPE)

When handling this compound, especially during disposal procedures, all personnel must wear appropriate personal protective equipment.

PPE TypeSpecifications
Gloves Chemical-resistant gloves (e.g., Nitrile, Neoprene).[4]
Eye Protection Safety glasses with side-shields or goggles.
Body Protection Long-sleeved shirt, long pants, and a lab coat.[4]
Respiratory Protection Avoid breathing fumes.[1] Use in a well-ventilated area. If ventilation is inadequate, use a suitable respirator.

Step-by-Step Disposal Protocol

The disposal of this compound must be handled as hazardous waste. Do not dispose of this compound in the general trash or down the drain.[1][5]

Experimental Protocol for this compound Waste Disposal:

  • Waste Segregation:

    • Designate a specific, clearly labeled hazardous waste container for this compound waste.

    • Do not mix this compound waste with other chemical waste streams unless explicitly permitted by your institution's environmental health and safety (EHS) office.

  • Containerization:

    • Use a chemically resistant, sealable container for all this compound waste. The container must be in good condition with no leaks or cracks.

    • For solid waste (e.g., contaminated wipes, gloves, or plasticware), double-bag the items in heavy-duty plastic bags before placing them in the designated solid waste container.

    • For liquid waste, use a labeled, leak-proof container.

  • Labeling:

    • Clearly label the waste container with the words "Hazardous Waste."

    • Include the full chemical name: "this compound Waste."

    • List all constituents and their approximate concentrations.

    • Indicate the specific hazards (e.g., "Toxic," "Reproductive Hazard").

    • Note the accumulation start date (the date the first piece of waste was placed in the container).

  • Storage:

    • Store the sealed and labeled waste container in a designated satellite accumulation area (SAA) that is under the control of the laboratory operator.

    • The storage area should be secure, well-ventilated, and away from sources of ignition or incompatible materials.

    • Ensure secondary containment is in place to capture any potential leaks or spills.

  • Disposal Request:

    • Once the waste container is full or has reached the storage time limit set by your institution (typically 90-180 days), contact your EHS office to arrange for a pickup.

    • Provide all necessary documentation as required by your institution for hazardous waste disposal.

Spill and Emergency Procedures

In the event of a spill, follow these procedures:

  • Evacuate: Immediately alert others in the area and evacuate if necessary.

  • Control: If it is safe to do so, prevent the spill from spreading using absorbent materials.

  • Personal Protection: Wear the appropriate PPE before attempting to clean up the spill.

  • Cleanup:

    • For solid spills, carefully scrape or sweep up the material and place it in the designated hazardous waste container.[1][5]

    • For liquid spills, use an inert absorbent material (e.g., sand, vermiculite) to soak up the spill.[2] Place the absorbent material into the hazardous waste container.

  • Decontaminate: Clean the spill area thoroughly with soap and water.

  • Report: Report the spill to your laboratory supervisor and EHS office.

Diagrams

This compound Disposal Workflow

cluster_lab Laboratory Operations cluster_ehs Environmental Health & Safety (EHS) gen Generate this compound Waste seg Segregate Waste gen->seg cont Containerize in Labeled, Sealed Container seg->cont store Store in Designated Satellite Accumulation Area cont->store pickup EHS Pickup Request store->pickup dispose Final Disposal at Approved Facility pickup->dispose

Caption: Workflow for the proper disposal of this compound waste.

References

Essential Safety and Handling Protocols for ST362

Author: BenchChem Technical Support Team. Date: December 2025

This document provides crucial safety and logistical information for the handling and disposal of ST362. Given that specific data for this compound is not publicly available, the following guidance is based on established best practices for managing hazardous chemical compounds in a laboratory environment. These procedures are designed to minimize risk and ensure the safety of all personnel.

Personal Protective Equipment (PPE)

A comprehensive hazard assessment should be conducted for any new substance.[1] However, as a baseline for handling potentially hazardous materials like this compound, the following personal protective equipment is recommended.

PPE CategoryRecommended Equipment
Eye and Face Protection Safety glasses with side shields are mandatory at all times.[2] If there is a splash risk, a face shield should be worn in addition to safety glasses.[1]
Hand Protection Chemical-resistant gloves are required. The specific type of glove material should be chosen based on the chemical properties of this compound, once determined. Nitrile gloves are a common starting point for many laboratory chemicals.
Body Protection A lab coat or chemical-resistant apron should be worn to protect against spills.[3] In cases of significant exposure risk, a full-body suit may be necessary.
Respiratory Protection Work should be conducted in a well-ventilated area, preferably within a certified chemical fume hood. If airborne concentrations of this compound are expected to exceed exposure limits, or if working outside a fume hood, a respirator may be required.[2]
Foot Protection Closed-toe shoes are mandatory in all laboratory settings.[1] For handling larger quantities or in pilot plant settings, steel-toed safety boots are recommended.[1]

Standard Operating Procedure for Handling and Disposal

1. Preparation and Engineering Controls:

  • Before handling this compound, ensure that all necessary PPE is readily available and in good condition.

  • Verify that the chemical fume hood is functioning correctly. Engineering controls are the first line of defense in minimizing exposure.[4]

  • Locate the nearest safety shower and eyewash station and confirm they are unobstructed.

  • Have a spill kit readily available that is appropriate for the volume of this compound being handled.

2. Handling this compound:

  • Conduct all manipulations of this compound within a certified chemical fume hood to minimize inhalation exposure.

  • When weighing this compound, use an enclosed balance or a balance within the fume hood.

  • Avoid direct contact with the substance. Use spatulas, forceps, or other appropriate tools.

  • Keep all containers of this compound sealed when not in use.

3. Disposal of this compound Waste:

  • All waste contaminated with this compound, including gloves, disposable lab coats, and contaminated labware, must be disposed of as hazardous waste.

  • Segregate this compound waste into clearly labeled, sealed containers. Do not mix with other waste streams unless compatibility has been confirmed.

  • Follow all institutional and local regulations for hazardous waste disposal.[5] The cost of disposal is often higher than the purchase price of the material, so minimizing waste is crucial.[5]

Experimental Workflow for Handling this compound

G cluster_prep Preparation cluster_handling Handling cluster_disposal Disposal prep_ppe Don Appropriate PPE prep_eng Verify Engineering Controls (Fume Hood, Eyewash) prep_ppe->prep_eng prep_spill Prepare Spill Kit prep_eng->prep_spill handle_hood Work in Fume Hood prep_spill->handle_hood handle_weigh Weigh this compound handle_hood->handle_weigh handle_exp Perform Experiment handle_weigh->handle_exp disp_waste Segregate Waste handle_exp->disp_waste disp_container Seal & Label Container disp_waste->disp_container disp_removal Follow Institutional Disposal Procedures disp_container->disp_removal end End disp_removal->end start Start start->prep_ppe

Caption: Workflow for the safe handling and disposal of this compound.

References

×

Featured Recommendations

Most viewed
Most popular with customers

Haftungsausschluss und Informationen zu In-Vitro-Forschungsprodukten

Bitte beachten Sie, dass alle Artikel und Produktinformationen, die auf BenchChem präsentiert werden, ausschließlich zu Informationszwecken bestimmt sind. Die auf BenchChem zum Kauf angebotenen Produkte sind speziell für In-vitro-Studien konzipiert, die außerhalb lebender Organismen durchgeführt werden. In-vitro-Studien, abgeleitet von dem lateinischen Begriff "in Glas", beinhalten Experimente, die in kontrollierten Laborumgebungen unter Verwendung von Zellen oder Geweben durchgeführt werden. Es ist wichtig zu beachten, dass diese Produkte nicht als Arzneimittel oder Medikamente eingestuft sind und keine Zulassung der FDA für die Vorbeugung, Behandlung oder Heilung von medizinischen Zuständen, Beschwerden oder Krankheiten erhalten haben. Wir müssen betonen, dass jede Form der körperlichen Einführung dieser Produkte in Menschen oder Tiere gesetzlich strikt untersagt ist. Es ist unerlässlich, sich an diese Richtlinien zu halten, um die Einhaltung rechtlicher und ethischer Standards in Forschung und Experiment zu gewährleisten.

Schnellanfrage

Name *

E-Mail *

Telefon

Land

Produktname

Menge *

Nachricht